具有容错功能的高效电机控制装置
王 壮 李涵锐 孙祥诗 黄雪萍 乌日嘎夫 高晗璎
(哈尔滨理工大学,黑龙江 哈尔滨150080)
随着经济的发展,大量的不对称和非线性负载出现,要求逆变器带负载的能力就比较高了,但传统的三相三桥臂逆变器在不对称负载和非线性负载的情况下很难输出三相对称电压。在传统三相三桥臂逆变器基础上发展起来的三相四桥臂逆变器,通过第四桥臂为零序电流提供通路,具有外接平衡及不平衡负载能力,因此在逆变电源,电能质量控制等领域得到了广泛的研究和应用。同样,三相四桥臂逆变技术在电机控制领域中也显示了巨大的应用前景,其提高可靠性的能力和容错能力已受到了国内外专家、学者们的日益关注。另外针对传统的永磁同步电机无传感器控制,应用滑模控制策略具有控制性能好、鲁棒性好的优点。本文在滑模观测器的基础上引入自适应控制,在保证系统扰动能力强的条件下,提出了一种新的模型参考自适应速度辨识方法,减少对电动机参数的依赖,使转速估计更加准确。
1 主电路功率拓扑结构
三相四桥臂驱动永磁同步电机的功率拓扑结构相比于传统三相三桥臂拓扑结构,增加了一个桥臂,为不平衡负载提供了一个中性线电流通路,如图1 所示。这种拓扑结构在正常运行时通过采用有效的控制策略能够平衡输出和抑制干扰,在缺相的情况下由于第四桥臂与电机的中线相连,从而为中线电流提供回路,通过采用适当的电机控制策略仍能维持电机正常运行。

图1 四桥臂主电路拓扑结构图
2 永磁同步电机无位置传感器控制
永磁同步电机在静止坐标系α-β 下的数学模型为:

式(1)中,iα和iβ分别为定子电流α-β 轴分量;uα和uβ分别为定子电压α-β 轴分量;eα、eβ分别为反电动势轴α-β分量;Ls和Rs分别为定子电感和定子电阻;Ψf为永磁体磁链;ωe为电机电角速度;θe为以电角度表示的转子位置角。
选取滑模面为:
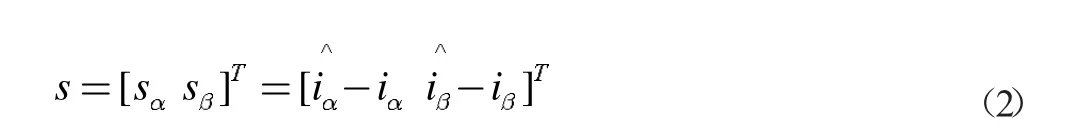
式(2)中,sα和sβ分别为α-β 轴定子电流误差;i赞α 和i赞β分别为定子电流的估计值。
本文采用光滑连续的sigmoid 函数来构建自适应滑模观测器,该sigmoid 函数为:

式(3)中:a 为一个正实数。
构建自适应滑模观测器如下:
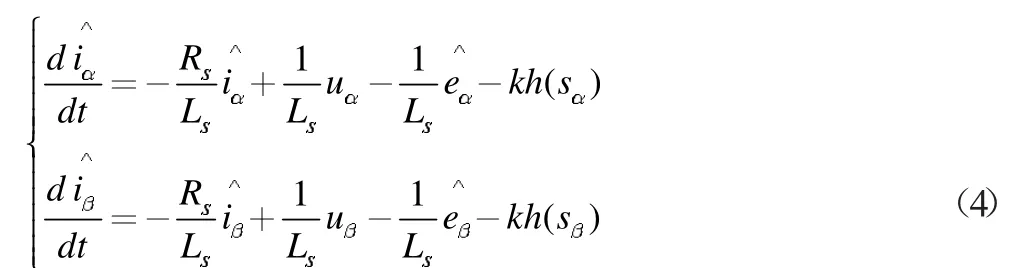
式(4)中,e赞α 和e赞β 为反电动势估计值;k 为观测器增益。
为使自适应滑模观测器稳定,同时为获取反电动势的估计方程,定义李雅普诺夫函数为:

式中,eα=e赞α-eα,eβ=e赞β-eβ,η 为正系数。
对(5)式求导,可得:
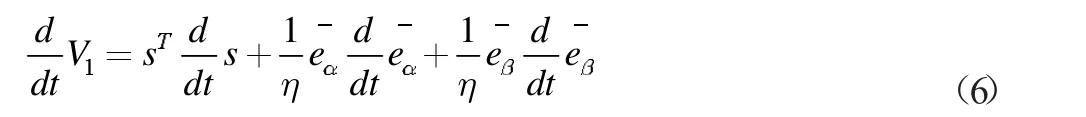
在一个控制周期内反电动势缓慢变化,把它看作为常数,即:
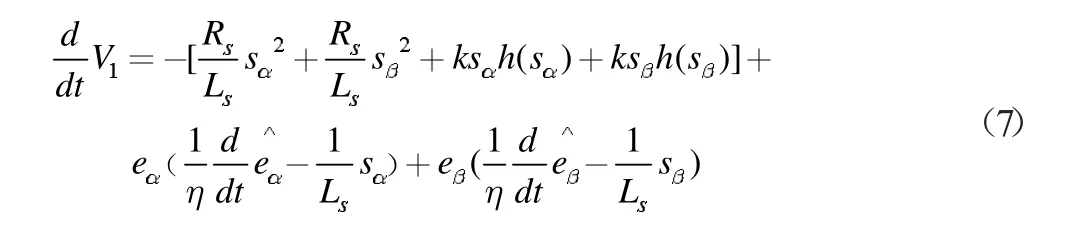
为使观测器稳定,需保证

3 系统仿真及结果
电 机 的 参 数 为:Rs=2.875Ω,Ldq=8.5mH,Ln=2.3mH,ψM=0.2135Wb,电机转动惯量J=0.00061kg/m2,转子极对数Pn=4,直流母线电压为300V,开关频率为10KHZ。仿真时间为0.1s。
在转速为15r/min 的前提下进行仿真实验。图2 为空间电压矢量调制波形,图3 为转子实际位置与估算位置波形,图4 为估算的反电动势波形。通过仿真可以看出基于本文方法得到的估计转子位置波形都较为光滑,基本不含高频抖振,估计反电动势波形较为平滑。
4 结论
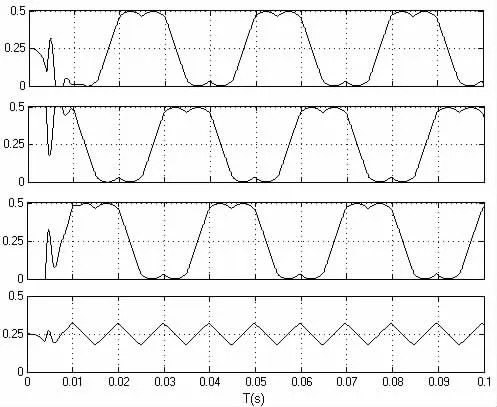
图2 空间电压矢量调制波形
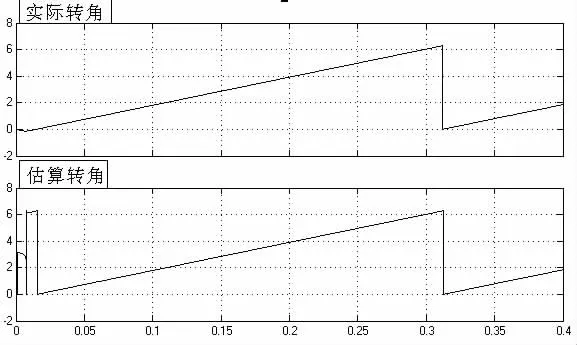
图3 转子实际位置与估算位置波形图
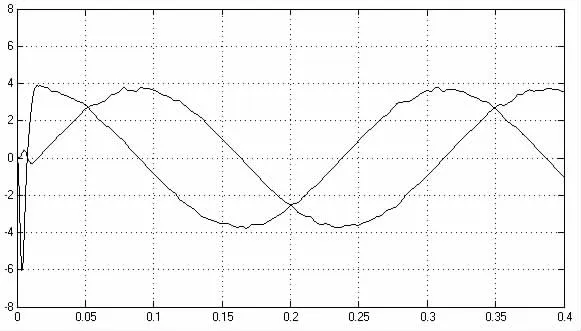
图4 估计反电动势波形
本文将电机三相四桥臂拓扑结构和自适应滑模观测器结合起来,实现了电机容错运行的无感控制。通过自适应滑模观测器,对电机的转子位置及转速估算较精确,特别是能够在较低速度区域很好地跟踪实际转子位置和实际转速。

