基于格理论的模糊度快速解算方法

王守华 ，吴黎荣 *，纪元法 ，孙希延

（1. 广西精密导航技术与应用重点实验室（桂林电子科技大学），广西桂林541004；2. 卫星导航定位与位置服务国家地方联合工程研究中心（桂林电子科技大学），广西桂林541004）

0 引言

随着全球卫星导航系统（Global Navigation Satellite System，GNSS）的融合和发展，各行各业对导航定位的精度、可靠性的需求越来越高，而高精度GNSS 定位通常是基于载波相位观测值进行的，这使得快速、准确地解算模糊度整型值成为了该领域的核心研究问题［1］。由于整周模糊度参数的离散性，通常都是基于模糊度的实数解及协方差矩阵构造出一定的搜索空间，再进一步采用搜索方法来获取模糊度的最优解，而现有的技术方法大多在高维情况下对此解算缓慢且成功率低。国内外学者均对此问题做了深入研究，先后提出了不同的模糊度解算方法，如模糊度函数法、最小二乘搜索法以及快速搜索法，这些方法都是直接采用搜索的技术获得模糊度的整型值。文献［2］中提出的最小二乘模糊度降相关（Least squares AMBiguity Decorrelation Adjustment，LAMBDA）算法的基本思想是通过整数变换降低模糊度的相关性，然后在整数变换的空间内采用搜索技术获得最优模糊度整型值；文献［3］中根据改进的球形搜索算法进行扩展，提出了改进的LAMBDA 算法（MLAMBDA），缩小了模糊度整型搜索空间，提高了模糊度的搜索效率；文献［4］中将格理论中的格基规约算法应用到模糊度实数解的降相关中，但由于当时各方面条件的欠缺，并没有通过实测数据来对算法理论进行分析。

本文基于格理论对GNSS 模糊度解算算法进行改进，并提出了最近格点（Closest Lattice Point，CLP）搜索算法对模糊度整型值进行搜索。该算法首先将模糊度搜索转化为对格中已知格点的最近格点搜索问题，再根据格基规约改进得出具有最小可能长度且相互正交的格基向量，最后采用CLP 搜索算法搜索出最优的模糊度参数值。

1 GNSS相对定位数学模型

对于GNSS 高精度定位双差模式下的观测方程，可以用下面通用的GNSS系统模型［5］来概括：

式中：L表示GNSS 双差观测值；b为观测模型中的实数未知参数，包括位置、对流层和电离层延迟参数；B 为其相应的系数矩阵；a 为模糊度未知参数；A 为其相应的系数矩阵；e 为观测噪声。

用最小二乘法对式（1）进行模糊度参数最优值估计，得：

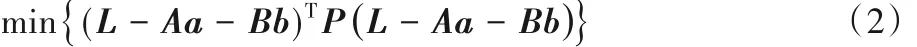
式中：P 是观测值的权重矩阵，通过忽略模糊度参数a 的整数特性直接求出方程中参数浮点解a^ 和b^，及其对应的协方差矩阵Qa^和Qb^。其中式（2）中的最小化问题可转化成如下问题：

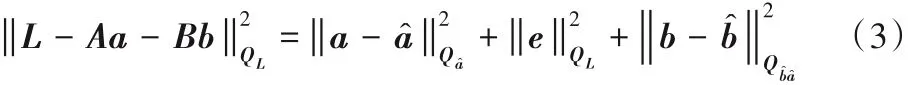
由于参数b 为实数，所以式（3）可以等价于右边两项最优估计，因此有

求解载波相位的模糊度最优值-a，最为经典的是基于最小二乘搜索的LAMBDA算法和在此基础上改进的MLAMBDA算法。

2 模糊度搜索与最近格点搜索的等价关系

由格的定义可知，设向量I 为一组格基向量且线性无关，则格的空间形式［7-9］可以表示如下：

式中，Λ(·)为格的数学表达式，如果格的所有格点α 相同，则格中的基本单元的容积大小不会因格基I 的变换而变化。根据这一思想可以通过格基规约对GNSS 模糊度的搜索区域进行搜索，但前提是构建与模糊度参数相关的格。

由格的一个著名问题知，对于一个已知的格中的点y，该点也许不是格点，那它肯定包含在由格基构成的实线性空间中，并在格中存在一个格点x满足：

其中格点x 被称为y 在格中的最近格点。对于求解这个最近格点的问题被称为最近格点搜索问题，格可看作是呈网格状以一个点一个点的形式存在于n 维空间，在整数单位二维情况下示意图如图1所示。

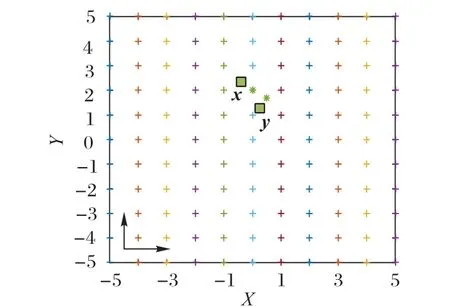
图1 给定点y的最近格点x搜索示意图Fig.1 Search diagram of the closest lattice point x for the given point y

由式（3）、（4）知，估计的模糊度参数最优值的协方差矩阵Qa^是正定的，因此权重矩阵P的Cholesky分解可以为：

式中R为下三角矩阵，同时式（4）的右式可以转化为：

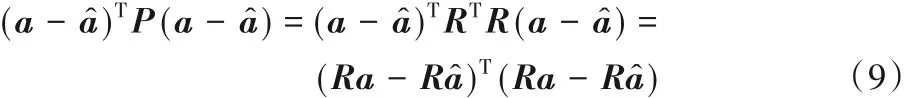
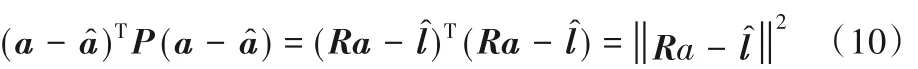
由式（9）、（10）可知式（4）最终可变换成：

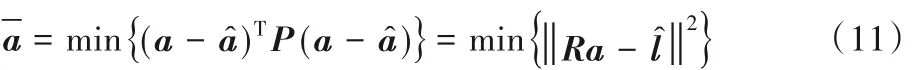
同时由式（7）的最小格点搜索问题知，对于给定的格中的点 y ∈ Rn，搜索出最接近 y 的格点 x，存在 α ∈ Zk，使得对于x ∈ Λ，x =|Iα|，有如下等式：

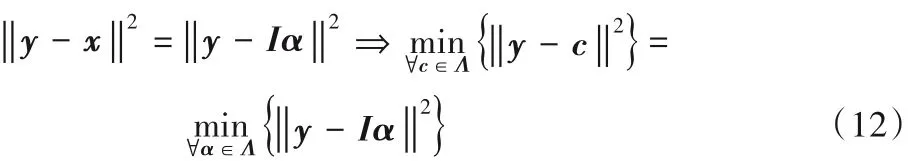
由式（11）和（12）可以得出，由最小二乘法搜索模糊度参数最优值等价于格上的最近格点搜索问题，因此可以将模糊度搜索转化为对格中已知格点的最近格点搜索问题。

3 改进的模糊度降相关处理

基于最小二乘法对模糊度参数解算时，为了消除参数的相关性会进行降相关处理。而对格中已知点的最近格点搜索时，往往采用格基规约，通过将给定的格基变换为另一个所需格基，且保持格的大小不变，搜索出具有最小可能长度且相互正交的格基向量。因此模糊度解算中的降相关处理等价于格基规约，现对格基规约的三个基本步骤：正交化、尺寸减小和格基变换进行改进。

由式（11）中矩阵P 的Cholesky 分解得出的下三角矩阵R进行Gram-Schmidt正交化得到：

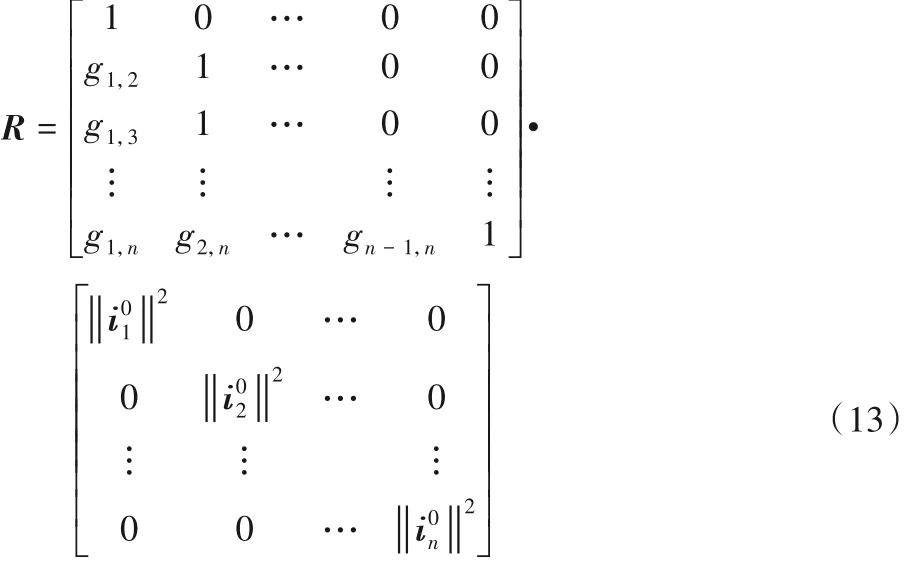
则由式（8）和（13）可得：

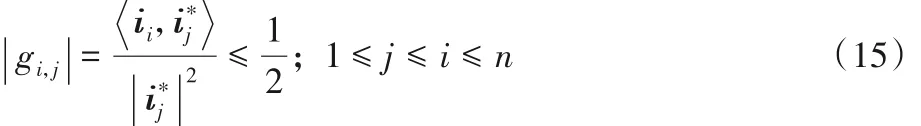
为了获得更好的尺寸减小，作出以下改进：格基中ii的顺序通过与对应的Gram-Schmidt 正交基元素i*i 变换来改变，为了得到对应的正交基i*i 更短的值，可以通过对ii和ii+1进行变换，连续向量ii和ii+1的格基变化条件如下：

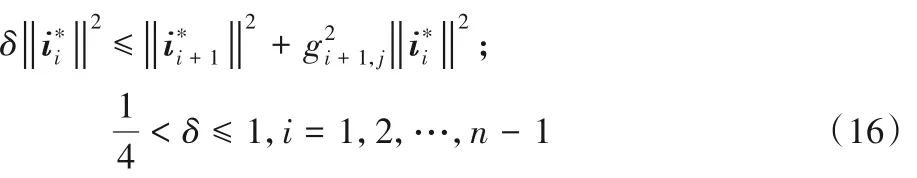
通过格基规约，对矩阵R进行规约，获得接近正交和最小长度的格基，在GNSS 定位解算中，基于矩阵R 获得的最小长度且正交的格基即为对应的模糊度参数值，由这一步提高了模糊度搜索的效率和成功率。

4 基于格理论的模糊度搜索算法

由第3章中已知点的最近格点搜索问题，令r0为以y为中心的n维粒子的平方半径，得：

同时由于R 为下三角形矩阵，不等式有下面一组条件关系：

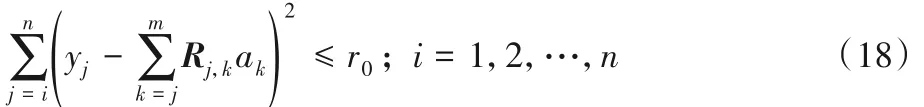
式中：Rj，k为矩阵R的第j行第k列元素；ak为对应的第k个需要固定的整数值，由于模糊度参数a值的整数特性，如果对于i +1 ≤j ≤n，aj表示已经固定的参数值，则变量ai（i = n - 1，n -2，…，1）可以在整数范围[Li，Ui]取整数值，区间范围如下：

式中：round(*)表示取最接近的整数值；yi为对应的第i个观测中心点；ak为第k个固定的整数值；Ri，j为矩阵R 中的第i行第j列元素。

而对于已经固定的aj(j = i + 1，…，n)的点，如果它们不属于以y为中心的半径为 r0的球体中，那这些点与y之间的欧几里得距离平方可表示为：

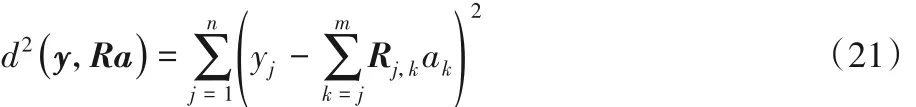
通过以上条件，本文提出了CLP搜索算法，并对整数范围[Li，Ui]搜索顺序分级别处理，其中对每个级别在区间的中点开始，以Z 字形顺序搜索，同时在搜索的过程中根据式（21）的限制条件估计确认是否继续搜索。先把r0设置为无穷大，设区间中点为Mi可得如下等式：

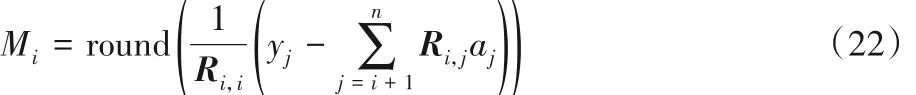
算法搜索的具体步骤可总结如下：

2）搜索过程从搜索第一个ai（i = n）开始，设此级别为第1级，生成的第一个格点设为aB，得出aB后，将r0设置为距离d2(y，Ra)。

3）再按照步骤1）开始搜索第2 级，对ai（i = n - 1）按照Z字形要求搜索得到整数点对应的最小搜索半径ri；若ri＜r0，则更新搜索半径，使r0= ri，再进行下一步。

4）依次对第3，4，…，n 级进行搜索，按Z 字形顺序搜索并得出整数点对应的最小半径，再与上一级得到的搜索半径进行比较，若小于，则对其进行更新，否则同理进行下一级搜索比较，直至未能在第n 级找到新的整数值时，搜索过程停止，则最小搜索半径的整数点对应的为最优整数解。

5 算例及仿真分析

5.1 数值模拟分析

为了验证本文提出的CLP搜索算法对模糊度搜索的有效性，基于Matlab 平台在不同案例情况对模糊度参数最优值搜索时间进行比较验证，针对不同案例，真实的模糊度参数浮点解a^ 被构造为：

其中randn(n，1)是Matlab内置函数，用于生成具有标准正态分布的n个目标向量。这些向量都根据真实模糊度参数特性构建而成，并构成如下7 种不同模拟案例，前四种基于模糊度参数协方差矩阵Qa^=LTDL，其中L是单位下三角矩阵，每个lij（对于i＞j）都是由randn生成的随机数。案例特点具体如下：

案例1：D= diag(di)，di= rand，其中rand是Matlab 内置函数，用于在（0，1）中生成均匀分布的随机数。

案例2：D= diag(n-1，(n- 1)-1，…，1-1)。

案例3：D= diag(1-1，2-1，…，n-1)。

案例4：D= diag(2 00，200，200，0.1，…，0.1 )。

案例5：协方差矩阵Qa^=UDUT，U是通过模拟的模糊度参数随机矩阵QR分解获得的随机正交矩阵，D= diag(di)，di=rand。

案例 6：Qa^=UDUT，U由与案例 5 相同的方式生成，其中U中的其他对角元素随机分布在di和dn之间，n是Qa^的维数。因此Qa^的条件数是

案例7：Qa^=ATA，A =randn(n，n)。

其中，每个案例都是有模拟理论的，如案例4，因为GNSS中的协方差矩阵Qa^通常在第三条件标准偏差和第四条件标准差之间存在较大差距，所以模拟下把其元素前后设置差距较大。在所有的模拟案例实验中，其他条件设置一致，且对参数的搜索成功率被默认为是100%，所有呈现的结果都在50次独立运行中执行。

表1 基于统计学原理统计出维度为40 时，CLP、LAMBDA和MLAMDA 搜索算法在模拟案例1～7 下50 次独立运行的平均搜索时间，而且每次运行中都统计到估计出参数最优值的搜索耗时。

表1 三种算法在模拟案例1～7上50次独立运行的平均搜索时间Tab.1 Average search time of three algorithms in 50 independent runs on simulation cases 1～7

由表1可知，模糊度维数为40时，CLP 搜索算法在模拟案例1～7 下50 次独立运行的平均搜索时间约为LAMBDA 的1/97、1/374、1/349、1/179、1/64、1/205、1/187，约为 MLAMBDA的1/6、1/5、1/6、1/6、1/7、1/7；且MLABDA 的平均搜索时间约为LAMBDA 的 1/16、1/78、1/56、1/23、1/11、1/27、1/26 倍。根据数值模拟结果可以得出对模糊度浮点解参数a^ 的最优值搜索，CLP搜索算法比LAMBDA和MLAMBDA的耗时更短。

图2 和图3 分别展示出CLP 搜索算法在案例1～7 进行50次独立运行的平均搜索时间和候选者数量，可见CLP 搜索算法搜索的平均时间和搜索的候选者平均数量是一一对应的关系。其中当维数为10～20 时，各种案例的搜索时间基本无差别，但随着维数的增加，其他案例的搜索时间都呈指数级增长，只有案例3 的搜索时间在相对稳定的范围内波动，且案例3 正好与CLP 搜索算法解算参数设置相一致，因此可以得出CLP 搜索算法即使在高维情况下，对于模糊度的搜索依旧高效稳定。

5.2 实测数据实验仿真

为了进一步验证CLP 搜索算法在实际场景下的效果，采用了两组不同时间段同一基线的GNSS 观测数据，使用Bootstrapping成功率作为模糊度解算的可靠性指标，按照上述相对定位数学模式对20 颗卫星进行单历元测试。其中实测实验条件为使用ublox M8T 型低成本接收机在某大学校园采集GNSS 观测数据，数据包含单频全球定位系统（Global Positioning System，GPS）和北斗导航系统（BeiDou navigation Satellite system，BDS）的载波相位、伪距观测量，如图4为一天中可观测的卫星数量（图中最上方曲线为GPS+BDS 卫星数）。其中，采集数据的两个观测站点固定不动，且观测环境相对较好，两站之间的距离约为100 m，位置坐标均采用静态后处理软件进行长时间解算得到。CLP 降相关处理时设置δ= 1，使得各算法基于Qa^=LTDL分解的降相关性能一致。数据采集时间段为 2019 年 3 月 18 日的 11 时 00 分到 13 时 00 分，共计7200历元，采样历元间隔为1 s。

在实际长时间解算中，算法存在抗干扰性差和不稳定性等问题。为了分析比较算法在对模糊度解算速度性能上的优势，选取其中两组不同实测数据实验得出三种算法的模糊度最优值的搜索时间和固定时间，结果如图5和图6所示。从图中可以看出，CLP 搜索算法的搜索时间稳定在0.01 s，LAMBDA 和 MLAMBDA 则分别为 0.052 s 和 0.03 s，且不稳定；当对模糊度固定解算时，增加去相关处理，固定时间相比搜索时间略有增加，搜索次数随着历元数的增加而迅速减小而后平稳，且都能明显看出CLP 搜索算法比LAMBDA 和MLAMBDA算法解算得更快。

图4 可观测卫星数Fig.4 Number of observable satellites

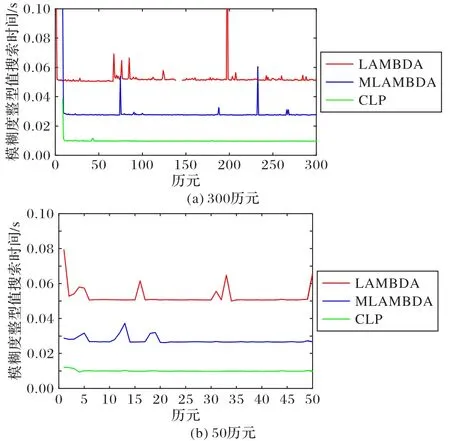
图5 三种算法在两组不同数据上的模糊度最优值搜索时间Fig.5 Search time for the optimal ambiguity by three algorithms on two different sets of data

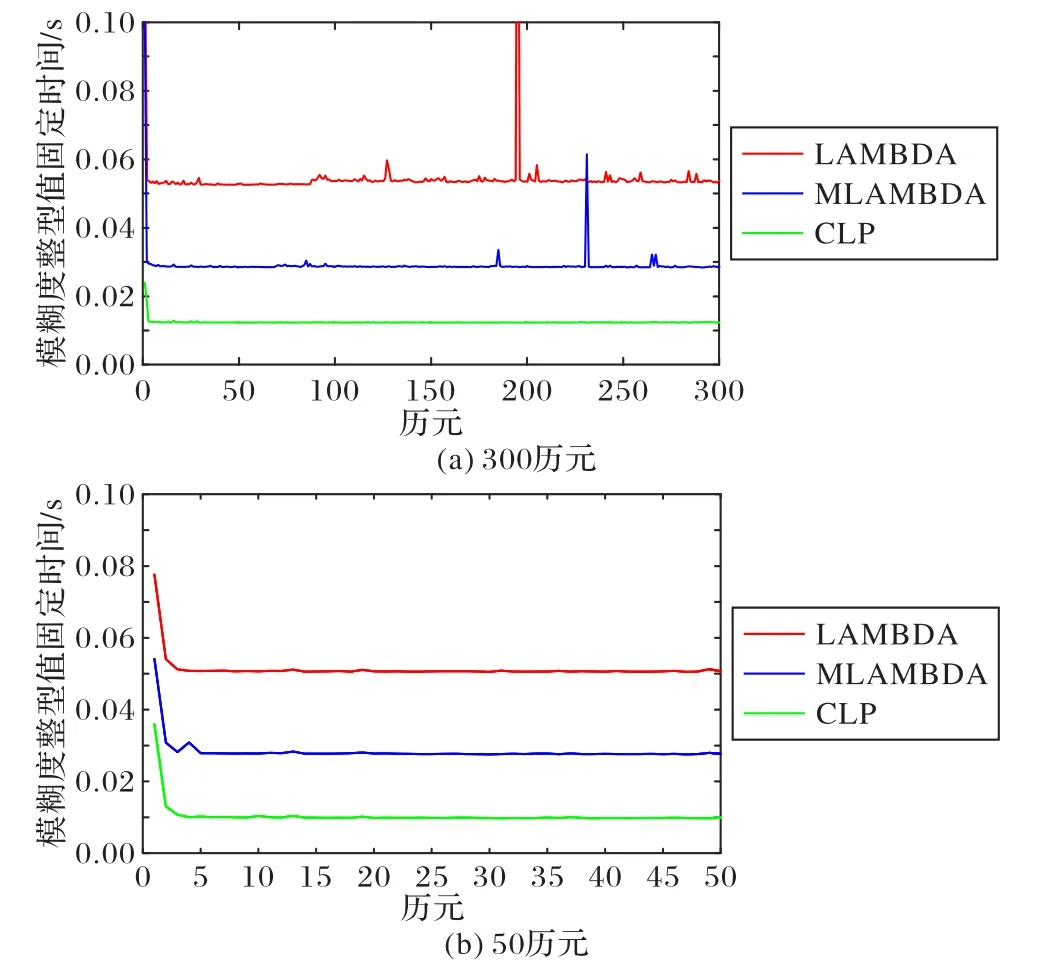
图6 三种算法在两组不同数据上模糊度最优值固定时间Fig.6 Fixed time for the optimal ambiguity by three algorithms on two different sets of data

6 结语

本文针对未来各GNSS 系统兼容与互操作，多频多模高维模糊度在常规方法下解算效率低的问题，基于格理论，对GNSS模糊度解算算法进行改进，并提出了CLP搜索算法对模糊度整型值进行搜索。该方法首先将模糊度搜索转化为对格中已知格点的最近格点搜索问题，再根据格基规约改进得出具有最小可能长度且相互正交的格基向量，最后采用CLP 搜索算法搜索出最优的模糊度参数值。通过模拟实验和实测数据实验验证得出，所提的CLP 搜索算法理论上相较经典的LAMBDA/MLAMBDA 算法对最优值模糊度参数解算效率更高、更可靠，且每一个参数搜索时间稳定在0.01 s，即使在高维情况下，CLP搜索算法的搜索依然稳定可靠。

基于格理论的模糊度解算方法的提出打破了常规解算思想，给未来多频多模系统的高精度解算提供了新的思路。本文主要针对GPS 和BDS 双系统情况进行解算，而对于多频多模GNSS 系统将进一步研究；同时在长基线情况下由于双差模型难以消除存在强相关性的参数之间的影响，致使分离模糊度参数耗费时间长且不可靠，解算结果是否依然有效可靠还需进一步研究。