因果推理†
况琨*,李廉,耿直,徐雷,张坤,廖备水,黄华新,丁鹏,苗旺,蒋智超
a College of Computer Science and Technology, Zhejiang University, Hangzhou 310058, China
b Department of Computer Science and Technology, HeFei University of Technology, Hefei 230009, China
c School of Mathematical Science, Peking University, Beijing 100871, China
d Department of Computer Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China e Department of Philosophy, Carnegie Mellon University, Pittsburgh, PA 15213, USA
f School of Humanities, Zhejiang University, Hangzhou 310058, China
g University of California Berkeley, Berkeley, CA 94720, USA
h Guanghua School of Management, Peking University, Beijing 100871, China
i Department of Government and Department of Statistics, Harvard University, Cambridge, MA 02138, USA
1. 平均因果效应评估—简要回顾及展望
机器学习方法已在许多领域取得了巨大成功,但其中大部分都缺乏可解释性。因果推理是一种强有力的建模工具,可用于解释性分析,其可能使当前的机器学习能够做出可解释的预测。本文回顾了两个用于估计因果效应的经典算法,并讨论了实际应用中因果效应评估存在的挑战。此外,我们提出了一种可能的方法,通过将因果推理与机器学习相结合来开发可解释的人工智能(explainable artificial intelligence, XAI)算法。
1.1. 问题和符号
基于潜在的结果模型[1],我们研究的问题是如何准确地评估治疗变量的因果效应。对于每个样本i (i = 1, 2,…, n),我们观测到其治疗变量Ti、结果变量Yi和特征变量Xi。基于治疗变量的取值(T = 1和T = 0),结果变量存在两个潜在结果Yi(1)和Yi(0)。实际观测到的结果Yiobs可表示为:
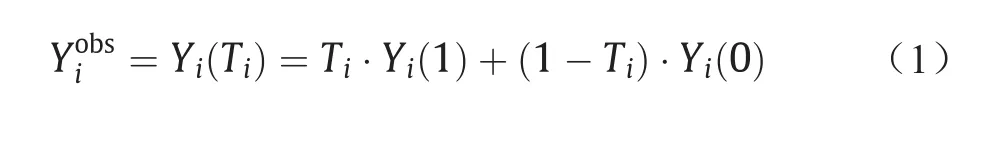
基于样本的潜在结果,我们可以定义治疗变量的评估因果效应为:
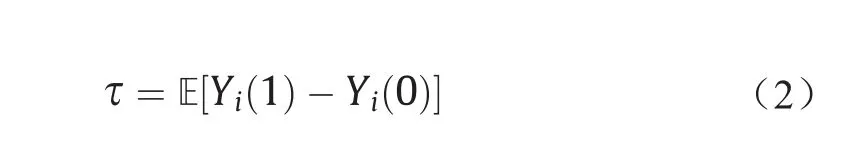
也可以定义在治疗样本(T = 1)上的平均因果效应为:
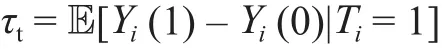
为了准确评估因果效应τ和τt,我们假设无混淆性Ti⊥[Yi(1), Yi(0)]|Xi和重叠性0 < p(Ti= 1|Xi) < 1。
1.2. 两类因果评估算子
在这里,我们简要介绍评估因果效应的两类常用方法,并讨论它们面对高维变量的扩展和应用。
1.2.1. 倾向值倒数加权
在完全随机的实验中,治疗随机分配到样本,意味着Ti⊥ Xi。然而,在观测数据中,治疗Ti是基于样本特征Xi指定的。为了消除Xi导致的混杂效应,倾向值表示为e(Xi)= (Ti= 1|Xi)来加权样本。基于倾向值,τ可以通过以下方式估算:
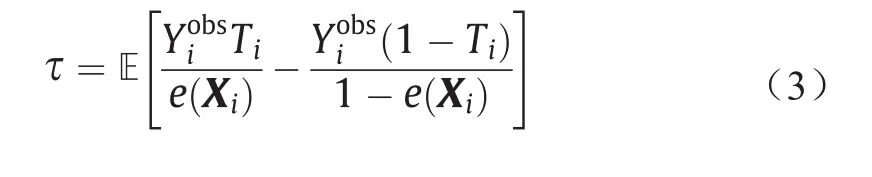
通过结合倾向加权和回归,我们还可以用双稳健方法估计治疗效果[2]。在高维情况下,并非所有观察到的变量都是混淆变量。为了解决这个问题,Kuang等[3]建议将所有观察到的变量分为两部分:混淆变量用于评估倾向值,调整变量用于减少估计因果效应方差。
1.2.2. 混淆变量平衡
消除混淆偏差的另一种常用的方法是通过直接样本加权来平衡治疗组(T = 1)和对照组(T = 0)之间混淆变量的分布,并将τt估计为:
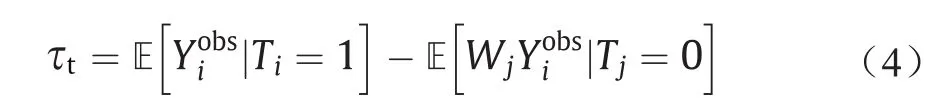
式中,样本权重W可以通过混淆变量直接平衡[4]学习得到,如下:
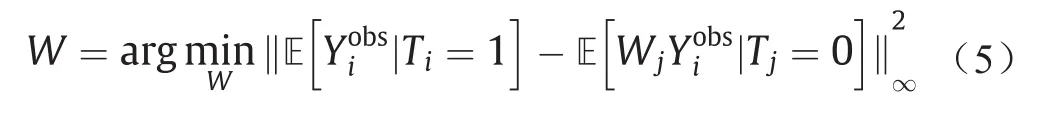
在高维情况下,不同的混淆变量可能导致不同的混淆偏差。因此,Kuang等[5]建议联合学习混淆变量权重用于区分不同的混淆变量,以及样本权重用于平衡混淆变量分布,并提出混淆变量区分性(differentiated confounder balancing, DCB)算法来评估因果效应。
1.3. 存在的挑战
最近,很多有效的方法用于在观察性研究中评估因果效应,但如何使这些方法在实践中变得有用仍然存在许多挑战,主要挑战表现在以下几个方面。
1.3.1. 治疗变量从二值到连续
现有算法主要用于评估二值治疗变量的因果效应,并在实际中实现良好的性能。但是在许多实际应用中,我们不仅关心二值治疗变量(治疗与否)的因果效应,更关心连续治疗变量的因果效应。
1.3.2. 多维治疗变量的相互作用
实际上,治疗可以由多个变量及其相互作用组成。在社交营销中,人们可能对不同广告策略的综合因果效应感兴趣。在支持治疗组合的因果分析方面还需要做更多的工作。
1.3.3. 未观察到的混淆变量
未观察到的混淆变量等同于违反非混淆性假设,并且它是不可测试的。控制高维变量可能使非混淆性假设更加合理,但对倾向值估计和混淆变量平衡提出了新的挑战。
1.3.4. 重叠性假设的限制
尽管重叠性假设是可测试的,但它在实践中会引起很多问题,包括如何检测变量分布中是否缺乏重叠,以及如何处理这种缺陷,特别是在高维度环境中。此外,估计因果效应仅适用于重叠性假设成立的样本区域。
为了解决上述挑战,最近,很多相关工作和算法被相继提出,包括连续治疗变量[6]、治疗变量的相互作用[7]、未观测到的混淆变量[8]以及重叠性假设的限制[9,10]。
1.4. 走向因果和稳定的预测
大多数预测算法缺乏可解释性,这使得它们在许多实际应用中缺乏吸引力,特别是那些需要决策的应用。此外,大多数现有机器学习算法都是关联驱动的,这导致它们在测试数据中的性能不稳定,因为测试数据的分布可能与训练数据不同。因此,开发可解释的并对来自未知测试数据的分布变化保持稳定预测的预测算法非常有用。
假设因果关系在数据集之间是不变的,那么合理的方法是探索因果和稳定预测的因果知识来实现可解释的稳定预测。受到来自因果推理文献中混淆变量平衡技术的启发,Kuang等[11]提出了实现因果和稳定预测的可能解决方案。他们提出了一个全局变量平衡正则约束项,以隔离每个预测变量的影响,从而恢复每个预测变量和结果变量之间的因果关系,用于指导机器学习算法的学习,实现在未知数据集中进行可解释的稳定预测。
总体而言,如何将因果推理与机器学习深入结合以开发可解释的人工智能算法是通往第二代人工智能[12,13]的关键,目前还存在很多问题、挑战和机遇。
2. 反事实推理的归因问题
本节中,原因变量x和结果变量y都是二值的。
反事实推理是因果推理的重要部分,简单地说,反事实推理是在事件x已经出现(x = 1),并且事件y发生(y = 1)的前提下,反过来推理如果事件x不出现(x = 0),则事件y不发生(y = 0)的概率,用公式表示为:
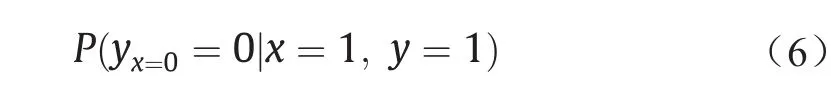
式中,yx=0是反事实推理的一个记号,表示如果x = 0时y的取值,与条件概率P(y|x = 0)是不同的概念。这个公式反映了没有事件x则没有事件y的概率,即原因的必要性(x作为y的原因)。这在社会科学或者逻辑科学中称为归因问题(attribution problem),在法律学上称为“若无准则”(but-for criterion)。归因问题已经有了比较长的研究历史了,但是以往的方法主要是社会科学的方法,如案例调查、统计分析、实验设计等,基本是定性的,且依赖于经验和直觉。随着大数据的出现,数据驱动的研究归因问题的定量化方法出现了,从而使得推理过程更加科学与合理。
归因问题另一个孪生的说法:在原因x未出现(x = 0),且事件y也未发生(y = 0)的前提下,如果原因x出现,那么事件y出现的概率为:
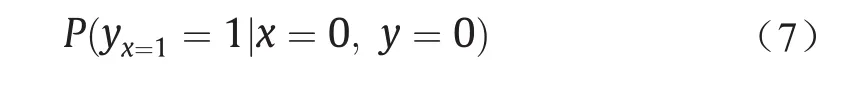
该公式反映了原因x导致事件y发生的概率,即原因的充分性。
在基于数据的推理研究中,原因的必要性和充分性是因果关系的不同侧面,尽管在计算公式上有所不同,但其基本精神是一致的。
反事实推理与人类的反思行为相对应,反思是智能活动的重要特征。推理使得人们在采取某个动作时,预测相应的结果,而反思却是在已有的结果面前,思考如何改进结果。反思虽然不能改变已经发生的结局,却可以为以后的行为提供修正,是用过去的知识指导未来行动的数学模型,只有具备了反思能力的智能才称得上是真正的智能。
反思在人类的日常生活中也是很重要的,例如,张某和李某同时做了癌症手术,张某又接受了放化治疗,结果两人都得到康复。因此张某就会反思,如果不做放化治疗,是否也能得到康复,显然我们不能因为李某的康复,就认为张某不做放化治疗也能康复。这类问题在医疗、法院审判等场合是大量存在的。我们关心对于具体的个案而言,当结果已经发生时,其原因究竟是什么。这时,一般的统计数据,如放疗成功率、交通事故率等并不能说明问题。通过归因推理计算某些原因的必要性在这些领域有着关键的意义[14]。
社会科学研究中有一个很有影响的关于因果分析的理论,即澳大利亚哲学家Mackie于20世纪60年代提出的INUS理论,INUS是Insufficient but Necessary part of a Unnecessary but Sufficient condition的缩写,意思是某个充分不必要条件下的必要不充分部分[2]。INUS理论认为,在事实集合X已经导致事实y发生的前提下(即X对于y是充分却可能不必要的),我们认为{x1, x2, …, xk}⊆X是y的原因,如果{x1, x2, …, xk}是X的必要却可能不充分部分。过去这一理论的语义上有很多不确定的成分,所用的方法是定性的,或者经验主义的,没有可行的算法用于量化计算。而在基于大数据的推理技术出现以后,这一理论赋予了准确的含义,并且可以通过算法进行定量描述。
关于式(6)的计算形成了反事实推理中的一个重要研究内容,目前还没有通用的计算该公式的方法。在实际问题中,引进一个很多情况下都能满足的所谓“单调性”假设:
yx=1≥ yx=0
单调性的直观意思是:采取某种措施(x = 1)后的效果y总不会低于未采取措施(x = 0)的效果。例如,在流行病学中,一个人不会在未采取隔离措施(x = 0)时健康(y= 1),在采取隔离措施后(x = 1)反被感染(y = 1)。由于单调性,式(6)通过推导得到:
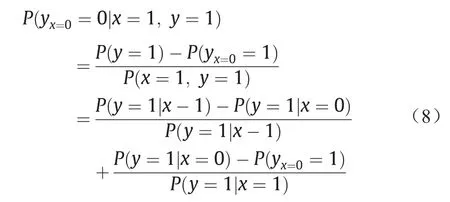
式(8)分为两项,前面一项是在风险统计中熟悉的归因风险部分(attributable risk fraction),或者也叫额外风险率(excess risk ratio),它反映了在x= 1和x= 0不同的措施下的风险率。而后一项就是特别要提出的混杂影响部分(confounding affect fraction),它反映了其他变量干扰的影响。P(yx=0= 1)称为do-操作,有时也写作P(y= 1|do(x= 0))。这是在实验(操纵)条件下,将其他变量固定,而单独考察x= 0时y= 1的概率。而条件概率P(y= 1|x= 0)表示自然条件下,x= 0时y= 1的概率(其他变量的值不作限制),P(yx=0= 1)和P(y= 1|x= 0)有着不一样的含义。在do-操作(实验条件下)时,我们看到的是x与y之间单纯的(因果)关系。而在自然条件下,y的变化来自两个方面,一个是x的变化直接引起的,另一个是通过其他变量间接引起的,这个现象称为混杂。两者之间的差P(y= 1|x= 0) -P(yx=0=1)表示了混杂的程度。混杂现象干扰了对于真正原因x的计算。在有些情况下,x的变化的确引起了y的变化,但x可能根本不是y变化的原因(如鸡叫之后太阳升起)。虽然我们可以通过科学实验来排除混杂,以便找出引起y变化的真正原因,但是在许多社会科学问题研究中,包括一些自然科学问题研究中,科学的实验是很难实施的,甚至是不可能的。我们手里能够得到的数据只有观察数据,因此如何从观察数据中识别混杂,以找出真正的因果关系是人工智能一项重要的研究内容。
为了更加具体地说明归因部分和混杂部分之间的关系,以及它们对于归因问题(原因的必要性)所起的作用,我们引用文献[15]中的例子。在这个例子中,赵某由于疼痛,去药店买了某种止痛药服用,结果死了。官司打到法院,要求药厂承担部分责任。药厂和原告律师分别出具了药品的检验结果(experimental)和市场调查结果(nonexperimental),如表1所示,其中,x= 1表示吃药,y= 1表示死亡。
药厂的数据来源于严格的药品安全实验标准,而律师的数据来源于市场调查,在患病的人里面根据自愿服药进行统计。药厂的理由是:药品已经通过检验,虽然吃药的死亡概率有所提高(由0.014提高到0.016),但是比起止痛效果而言,这点提高还是可以接受,并且符合药品上市的规定,因此根据传统的风险归因计算(额外风险率),药厂承担的责任是:
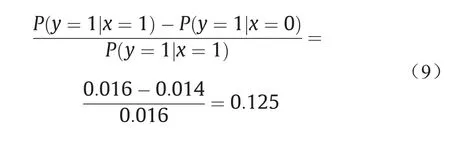
律师的理由是:药品的检验是在随机选择的条件下进行的,并没有征求受试者本人的意愿,因此实验是有偏置的(bias),并不符合实际服药情况,而市场调查的观察数据则是完全自愿的,未受到任何干预。从数据中看出,观察数据与实验数据相差很大。在赵某已经死亡的前提下,药厂的责任(即如果不吃药就会不死亡的概率)应该按照反事实的公式计算,其结果为:

因此药厂应对赵某的死亡负全责。
表面上来看,对于市场调查的数据,吃药而死的只占0.2%,而不吃药死亡的占了2.8%,非常有利于药厂(药厂的风险责任是-13,比实验数据还要好),但是仔细分析后,由于混杂成分占了P(y= 1|x= 0) -P(yx=0= 1) = 0.014,也就是有一半的人,不是因为未吃药而死亡,是因为其他原因死亡,因此这部分的功劳不能归因于药品,由此提升了药厂的责任。当然,在这个例子中,药厂的责任是否真的就是100%,以及计算公式的合理性与科学性还有一些质疑[16]。但是,这个案例说明在观察数据中存在的混杂变量会干扰真正的因果发现,而如何有效地识别混杂现象是因果推理中的现实问题,也是反事实推理中具有实际意义的问题。

表1 药品诉讼案例的检验结果和市场调查结果
在数据科学里,数据包括人为生成的数据和客观产生的数据。在客观产生的数据中又有实验数据和观察数据,前者是在实验条件下所搜集的数据,后者是在自然条件下搜集的数据。观察数据虽然客观、易于获取、成本较低,但是其中的混杂问题往往构成了因果推理的障碍[17]。特别在客观世界中可能还会有未知的变量(即隐变量),这些变量我们未能观察到,同样可以对已知的变量发生作用,这种情况称为非测定混杂。或者说,已知变量对于隐变量带来的非测定混杂可能是敏感的,目前的研究还处于十分初步的阶段,希望了解更多细节的读者可参考文献 [18]。
3. Yule-Simpson悖论和替代指标悖论
两个变量的相关性可能会由于忽略了第三个变量而发生非常大的变化,甚至可能从正相关变为负相关,这个现象称为Yule-Simpson悖论[19,20]。第三个变量是一个混杂因素。表2给出了一个数值例子。风险差(risk difference,RD)定义为吸烟组患肺癌比率与非吸烟组患肺癌比率的差值:RD = (80/200) - (100/200) = - 0.10,其值为负。表 3给出了将这400人按照性别分组的结果。可以看到按性别分组后,发生了很大变化,男性组和女性组的风险差都变成正的,即0.10。这意味着吸烟分别对男性和对女性都有害,但是吸烟对人类有益。
与相关性推断的关键区别在于,因果推断必须考虑是否可能存在影响处理变量和结果变量的公共原因,称为混杂因素。混杂因素可能导致推断因果作用时产生混杂偏倚。在试验性研究中,我们可以设计试验方案,根据某些变量的水平制定处理或暴露的分配概率;在随机化试验中,给每个个体随机地分配处理和暴露,没有影响处理分配的变量,因此不存在混杂因素。在观察性研究中,为了进行因果推断,需要观测充分多的混杂因素,或者观测一个独立所有混杂因素的工具变量。可是,利用观测到的数据不能确认是否观测到了充分多的混杂因素或工具变量。根据观察性研究得到的数据进行因果推断时要求一些假定,这些假定是不能用数据检验的。

表2 吸烟与肺癌的关系
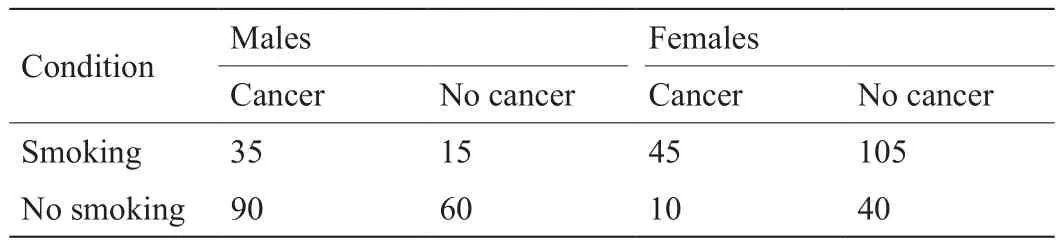
表3 吸烟与肺癌的关系:按照性别的分类
当感兴趣的终点指标不易观测时,取而代之观测一个替代指标(如生物标记物),然后用替代指标的因果作用预测处理未观测终点指标的因果作用。目前,已经有各种选择和确定替代指标的准则。但是,这些准则难以避免替代指标悖论,即处理对替代指标有正的因果作用,而且替代指标对终点指标也有正的因果作用,但是,处理对终点指标反而有负的因果作用[21]。文献[21,22]给出了替代指标悖论的数值例子。这个悖论也质疑了科学知识是否对决策分析有用[23]。有一个著名的实例,医生知道心律失常是猝死的危险因素,因此,临床试验将心律失常作为猝死的替代指标。但是,一些能有效纠正心律失常的药物,后来发现不但不能减少猝死,反而导致数万人过早死亡[24]。如何选择和确定替代指标的准则还有待于进一步研究。
Yule-Simpson悖论和替代指标悖论告诉我们:从数据得到的结论可能会被未观测的混杂因素逆转。这两个悖论还强调了获取数据方法的重要性。首先,随机化试验是因果推断的金标准。其次,如果不能采用随机化试验,试验设计需要试图平衡处理组和对照组的混杂因素。再次,可以考虑鼓励试验方法,随机地鼓励一部分人接受处理或避免暴露,使得这些鼓励能够改变他们处理和暴露的概率,实际上这种鼓励试验方法设计了一个工具变量“鼓励”。最后,对于纯观察性研究,我们不得不根据专业知识论证因果推断所要求的假定,并且采用敏感性分析探讨偏离这些假定的情况下影响因果推断结论的程度。这两个悖论还指出了三段式推理和传递性推理也许不能应用于统计得到的总体结论。统计得到的总体结论也许会出现这样的现象:吸烟对男性和女性都有害,尽管任何一个人不是男人就是女人,但是,吸烟对人也可能有益;药能纠正心律失常,纠正心律失常可以延长寿命,但是,该药也许会缩短寿命。
4. 因果发现CPT方法
如何从观察数据中发现和分析因果结构,近百年来研究者已做了广泛努力。大致都沿着一个类似的思维方向。首先,对欲观察的多个变量先假设一个因果结构,它直接或间接地描述这些变量的概率分布,而变量间关系反映因果关系。最简单的情况是一个单变量随机模型x→y,而复杂情况下为一个有向无环图(directed acyclic graph,DAG),并满足某些约束条件。然后,通过观察数据学习模型中的未知参数,监测模型能否最佳描述观察数据,并满足主要的约束条件,从而检验模型和因果方向的正确性。常用方法包括Rubin因果模型、结构方程模型、函数因果模型、非线性可加噪声模型、线性非正态无环模型、后非线性模型、型结构发现模型[25]和ρ图方程模型[26]。
最近提出的因果势理论(causal potential theory, CPT)源于很不同的思维[27]。回归物理学,因果关系被视为由某种势能引起的内在动力学性质。环境U中一对变量x和y之间的因果关系,并不简单的是这对变量间的局部关系,而是全局趋势在二元关系上的投影。无需事先假定因果结构,从x和y的样本估计非参数分布p(x,y|U),再通过吉布斯分布获得对应的因果势能E(x,y|U) ∝ -lnp(x,y|U)。发生在x和y处的事件,源于动力学[x.t,y.t]∝[gx,gy],这里记号。该动力流推向能量最低处或可能发生事件的区域。如表4所示,可以通过对gy和x之间以及gx和y之间的独立性检验判定因果方向,或者无向,也可以近似检验二阶独立,即相关系数是否为0。两个检验可用多元检验方法联合进行。
估算p(x,y|U)也可不用非参数方法,而是通过某种参数模型,还可通过x和y的样本直接估算[gx,gy],尤其是考虑在环境U下如何估算p(x,y|U)。进一步发展是探讨估计多个变量分布和多个变量之间的因果结构。下面介绍沿两个方向的可能发展。
(1)回顾PC算法[28]。通过独立和条件独立检验,发现DAG因果结构,其中考虑如何集成表4的CPT检验。当PC算法要剪的边与表4中结论冲突时,若x,y在第三变量条件下独立,则不剪边;即使x,y独立也不急于剪枝,可判为弱定向。
(2)分三步进行TPC学习[26]。一是用PC算法或上述集成,获得DAG的Topology。二是考虑变量间相关系数ρ进行路径分析,得到所谓的ρ图方程组,如文献[26]中的式(29)和式(33),形成一个变量约束在[-1,+1]间的多项式方程组,然后用Wu的方法来求解所有未知的ρ参数。若方程组有唯一或有限个解,表示对应的DAG有全局且定量的支撑。若没有解,则加入新的边或变量;若有无限多解,则剪掉某边或变量。三是用CPT(表4)确定每个边的Casual方向。然后,对于剩下的未能定向的边,再用类似PC的算法对ν节点进行处理。
5. 从观测数据中发现因果关系
因果性是科学中的一个基本的概念,它在提供解释、预测以及决策和控制中扮演着重要的角色[28,29]。现代因果关系的研究中,有两类本质的问题需要解决。一类大致称为“因果推断”——假设已有部分或完全的因果结构,如何估计一个变量对另一个变量的因果影响的大小?关于这类研究,有兴趣者可参考文献[29]及其所引文章。该类问题常假设因果结构已知,但我们怎样才能知道因果关系?为找到因果关系,传统的方式是求助于人为干涉或者随机试验,但这在很多情况下太昂贵、太费时,甚至现实中不可行。因此,越来越多的人开始重视“因果发现”——通过分析被动观测的数据找出背后的因果关系。在过去30年,因果发现这一领域取得了很大进展,这部分归功于计算机技术的进步。这些进步包括收集、存储大数据的能力以及计算速度的提高。在一些领域,我们需要用到天气卫星图像、核磁功能扫描图像,或基因表达数据,变量的个数可达百万之多,而且一般情况下用来减小因果假设搜索空间的背景知识是很少的。若没有自动搜索,因果发现的实用性会极其受限。越来越快的计算机,以及大的内存和存储空间,使得因果发现的自动搜索算法可以处理大规模的实际问题。
统计学中有一个脍炙人口的说法——因果性蕴含了相关性,但相关性并没有蕴含因果性。我们觉得后半句改成“但相关性并不直接蕴含因果性”会更公允。事实上,现在已经清楚地看到,在适当的假设下,通过分析观测数据可以找出部分或者完整的因果结构信息(通常用有向图表示)。从20世纪90年代开始,数据中的条件独立性已被用作约束条件来重构因果信息。这类基于约束的方法包括PC (Peter-Clark)算法和快速因果推理(fast causal inference, FCI)算法[28]。如果假设给定系统没有混淆因子(混淆因子的定义是给定系统中两个变量的未观测到的直接的因),那么PC算法的结果是渐进正确的。即使存在混淆因子,FCI算法的结果亦渐进正确。只要有可靠的条件独立检验的方法,这类算法可以处理各种因果关系和数据分布,所以有较广的实用性。但同时,它们的结果往往并不包含全部的因果信息——它们的输出结果是(独立)等价类。作为一个集合,这个类包含了所有具有同样的(条件)独立关系的因果结构。若假设没有混淆因子,还存在结果渐进正确的基于分数的方法,这些方法通过优化恰当的分数来搜索因果结构。这类方法中,贪婪等价类搜索(greedy equivalence search, GES)可直接在等价类空间进行搜索,因此已经得到很多应用。

表4 CPT因果关系分析的两条路
在过去13年间,人们更进一步地发现基于恰当定义的函数因果模型可用来区分等价类中不同的因果结构。这个进展归功于关于因果机制的额外假设。函数因果模型把果变量Y写成直接的因X和噪声E的一个函数,数学描述是Y=f(X,E),这里E和X是相互统计独立的。如果在f上没有任何约束条件,那么对于任意两个给定的变量,其中一个总能被写成另一个变量以及与之独立的噪声的函数。如此一来,因果的不对称性就没法得以体现[30]。幸运的是,如果我们恰当地约束函数类,就能找到X和Y之间的因果方向。这是因为若在错误的方向上估计因果模型,估计出的噪声和假设的因之间不可能统计独立,而在正确的方向上它们是独立的。这些函数因果模型类包括:
(1)线性非正态无环模型(linear non-Gaussian model,LiNGAM)[31]:它假设因果关系是线性的,而噪声是非正态的。
(2)后非线性模型(post-nonlinear, PNL)[32]:它考虑了因的非线性影响以及经常存在的测量过程非线性变形。
(3)非线性可加噪声模型(additive noise model,ANM)[33,34]:它描述了因的非线性影响并假设噪声是可加的。
若对如何用这些方法区分因果以及如何用它们从多个变量找到因果图感兴趣,可参考文献[30]。
因果发现是通过分析观测到的数据实现的。这些数据是由背后的因果过程以及观测和采样过程产生的。因此,在解决实际问题时,我们需要考虑因果过程以及观测过程带来的挑战。比如,从神经心理学中常用的血糖依赖水平(blood-oxygenation-level-dependent, BOLD)时间序列来发现背后的因果过程并不容易,部分由以下原因导致:因果交互可能是非线性的;数据的采样率跟背后的动态过程相比太低了;因果模型中可能存在反馈回路;过程具有非平稳性;可能存在混淆因子。在临床研究中,我们常常有很多缺失数据。网上收集的数据或者医院采集的数据一般都有选择偏差。有些数据集里面同时有类别变量(或离散变量)以及连续变量,这可能让条件独立检验以及寻找合适的函数因果模型类别变得困难。近年来这些问题基本都已引起注意,也出现了一些相应的处理方法。
机器学习的发展已经促进了因果发现的研究,因为机器学习为从数据中找寻信息提供了基本工具。另一方面,因果信息描述了过程的性质,从而提供了关于数据分布的一系列约束条件,而这些约束条件可帮助我们更好地理解和解决数据分布有变化时的机器学习问题。特别是若要从异构数据中学习有用信息,我们很自然地需要学习数据异构的性质,并为之建模,而这一步可受益于因果模型。这类问题包括领域适应(或迁移学习)[35]、半监督学习,以及从正类和无标记样本中学习。最近几年,利用因果模型帮助建立推荐系统以及进行强化学习也慢慢引起重视。
6. 形式论辩在因果推理和解释中的作用
在本节中,我们将以概述形式讨论论辩为何以及如何在因果推理和解释中发挥重要作用。形式论辩通过构造论证、比较论证和评估论证来实现推理[36]。论证通常由一个主张以及支持该主张的前提组成。前提可以是观察信息、假设或其他论证的中间结论。主张、前提和它们之间的推理关系都有可能受到攻击[37]。当一个论证能抵御所有攻击时,它才能够被接受。在人工智能领域中,形式论辩是建模可废止推理的一般形式,它为证明和解释因果关系提供了一种自然的方式。形式论辩也是机器学习的补充,可用于学习、推理和解释因果关系。
6.1. 非单调性和可废止性
因果推理是确定因果关系的过程。因果关系(即原因和结果之间的关系)通常是可废止和非单调的。一方面,因果推理规则通常是可废止的。因果规则可以用“c引起e”来表示,其中,e是某种结果,c则是一个可能的原因。因果联结词并不是实质蕴涵的,而是带有强度和可能性的可废止条件式。例如,“转动点火开关是引起发动机启动的原因,但这并不意味着发动机一定会启动,因为发动机启动还和其他因素相关,如是否有电池,电池是否有电,是否有燃气,等等”[38]。另一方面,因果推理是非单调的。这意味着我们只能暂时得到因果关系,当我们得到更多的信息时,之前所获得的因果关系可能会被推翻。通常情况下,c引起e,但是c和d却不能引起e。例如,一个主体认为转动点火开关会使电动机启动,但是当该主体知道电池已经没电了,则不会相信转动点火开关会引起电动机启动。在人工智能中,这就是著名的条件问题(qualification problem)。由于一些潜在的相关因素通常是不确定的,所以进行明确的推理并不有效。因此,当进行因果推理时,人们通常会“跳”到结论,并在需要时推翻一些结论。类似地,从证据到原因的推理是非单调的。如果一个主体观察到一些结果e,则可以假设一个可能的原因c。由事实到原因的推理是溯因推理。对于某些事实来说,如果没有更好的解释,则接受溯因解释。然而,当产生一些新的解释时,旧的解释也可能会被丢弃。
6.2. 高效性和可解释性
从计算的角度看,单调性是经典逻辑的一个重要性质。它意味着利用知识的子集进行局部计算得到的每一个结论都等于利用所有知识进行全局计算得到的结论。然而,这一性质在非单调推理中并不成立,因此其计算效率可能非常低。在提高计算效率方面,比起其他一些非单调形式体系(如缺省逻辑和限制逻辑等),形式论辩已被证明是一个良好候选。其原因在于,在形式论辩中,可以采取分而治之的策略,以及依据论证图中节点的可达关系,最大限度地利用已有的计算结果[39]。在人工智能中,因果推理的另一个重要特性是可解释性。传统的非单调形式系统在用于解释方面并不理想,因为其中所有的证明都并非以人类可理解的方式来表达的。由于解释的目的是为了让人们能够更好地理解,比较和对比论证的认知过程具有十分重要的意义[37]。以辩护和论证对话的方式,论辩通过交换论证的方式提供了这样的一种途径[40]。
6.3. 与机器学习方法的联系
在可解释人工智能中,包含两个部分:可解释模型和解释接口。后者包括直接来自模型的自反解释和来自对用户信念进行推理的理性解释。为了实现这个目的,一种自然的方式是将论辩与机器学习结合起来。其中,知识通过机器学习获得,而推理和解释则通过论辩来实现。由于论辩提供了一种在不一致情景下进行各种推理的一般形式,并且可以与概率和模糊性等一些不确定性度量相结合,因此它能够灵活地对从数据中得到的知识进行建模。当机器学习一些特性并做出解释时,例如,“这张脸很生气,因为它与这些例子相似,而与另一些例子不同”,这就是一个论证,它可能会受到其他论证的攻击。并且,要衡量类似“愤怒”这样的词所描述的不确定性,人们可以选择使用可能性论辩或概率论辩[41]。不同的解释可能相互冲突。例如,在某些情况下,我们可能会采用支持某个选择的特定示例或故事,从而拒绝对另一基于分析、案例和数据的次优选择。通过使用论辩图,可以方便地对这类支持和攻击关系进行建模,从而计算不同选择下冲突论证的状态。
7. 复杂实验中的因果推断
因果推断的潜在结果框架始于一个假想的实验,在该实验中,实验者可以将每个样本分配到多个处理水平。每个样本都有与这些处理水平相对应的潜在结果, 而因果作用就是对同一组样本之间潜在结果的比较。这种方法有时被称为实验主义者的因果推断方法[42]。读者可进一步参考文献[43-46]。
7.1. 随机因子实验
Neyman [47]首先用数学严格讨论了如下的随机化模型。一个实验有n个样本,实验者随机分配(n1, …, nJ)个样本接受处理水平(1, …, J),其中n =。样本i有潜在结果{Yi(1), …, Yi(J)}:如果样本i接收处理水平j,那么Yi(j)是对应的结果。基于潜在结果,我们可以定义因果作用。比如,干预水平 j和 j′之间的比较为{Yi(j)-Yi(j′)}。如果样本i实际接收到了处理水平j,则定义二值指标Ti(j)为1,用Ti(j)Yi(j)表示样本i的观测结果。根据观测数据{Ti(1), …, Ti(J)}ni=1,Neyman [47]建议使用作为τ(j, j′)的估计量。他证明τ^(j, j′)是无偏的,方差为S2(j)/nj+ S2(j′)/nj′- S2(j -j′)/n,其中S2(j)、S2(j′)和S2(j - j′)是Yi(j)、Yi(j′)和Yi(j) -Yi(j′)的样本方差。注意,所有潜在结果都是固定的,这个问题的随机性来自于二值的处理指标。Neyman [47]进一步讨论了方差估计和大样本置信区间等问题。
我们可以将Neyman [47]的框架推广到一个更广泛的因果作用表示个体作用,而cj是满足= 0的比较矩阵。只要适当选择比较矩阵,这个定义就包含了方差分析[48]和因子实验[49,50]。此外,只要适当选择样本子集,这个定义也包含了亚组分析、事后分层[51]和同侪效应[52]。文献[53]提供了在这种框架下渐近统计推断所需的中心极限定理的一般形式。文献[54]讨论了裂区设计,文献[55]讨论了更广的实验设计。
7.2. 协变量在分析实验数据中的作用
Neyman [47]的随机化模型也允许在没有强建模假设时使用协变量提高估计精度。在处理为二值的情况下,对于样本i,用{Yi(1), Yi(0)}表示潜在结果,Ti表示二值处理变量,xi表示协变量。平均因果作用的一个无偏估计量为[56]建议使用协方差分析以提高估计精度;也就是用Yi对Ti和xi拟合一个最小二乘,然后使用Ti的系数去估计τ。在文献[47]的模型下,文献[57]证明Fisher的协方差分析的估计并不一定好,它的估计精度甚至比τ^还低,而且最小二乘法可能给出不相合的方差估计。文献[58]提出一个简单的修正:第一步,中心化协变量,使平均值为零,x = 0;第二步,用Yi对(Ti, xi, Ti× xi)拟合一个最小二乘,然后使用Ti的系数去估计τ;第三步,使用Eicker-Huber-White方差估计值[59-61]。在大样本下,文献[58]的估计至少和τ^一样有效,并且Eicker-Huber-White方差估计是τ^真实方差的保守估计。
文献[62]将分析推广到高维协变量,并用文献[63]提出的最小绝对收缩和选择算子(least absolute shrinkage and selection operator, ASSO)替换了最小二乘。文献[64]研究了文献[58]中最小二乘估计值的理论边界,考虑了协变量个数可能发散的情形。文献[65]用Yi在(Ti, xi, Ti×xi)上的最小二乘拟合来研究处理作用的异质性。文献[66]讨论了因子实验中的协变量调整,而文献[67]讨论了更广的实验设计中的协变量调整。
7.3. 协变量在实验设计中的作用
分析人员可以使用协变量提高估计效率。与之对偶,设计人员可以用协变量改善协变量平衡,从而提高估计效率。文献[68]暗示了重新随机化的思想,也就是只接受那些能确保协变量平衡的随机分配。考虑一个特殊的例子:我们接受随机分配当且仅当且a > 0,并且是一个预定常数时。文献[69]正式地讨论了这个重新随机化在处理组和对照组有相同样本量,协变量为正态分布,且处理作用为常数时的统计性质。文献[70]在没有这些假设的情况下研究了τ^的渐近理论。文献[70]证明τ^具有一个非正态的极限分布, 并且它在重新随机化下比在完全随机化下更接近于τ。文献[70]中的结果表明当a≈ 0时,重新随机化下τ^的渐近方差与完全随机化下[58]提出的估计量的渐近方差几乎一样。因此,我们可以把重新随机化看作是回归调整的对偶。
文献[71]提出一个能反映不同协变量重要性的重新随机化方案,文献[70]分析了该方案的渐近性质。文献[72,73]将重新随机化扩展到因子实验,文献[74]提出了序贯重新随机化。
7.4. 结语
受到文献[47]的启发,这一节重点回顾了随机实验中估计量的重复采样性质。另外,在所有的样本都满足Yi(1)= … = Yi(J)的强零假设下,对于任何检验统计量和任何实验设计,Fisher随机化检验都是在有限样本下精确的假设检验[46,75,76]。文献[77,78]提出了在随机化检验中使用协变量调整的方法,文献[69]提出用随机化检验分析重新随机化。文献[79-81]将随机化检验应用于有干扰的实验。文献[48,50,82]讨论了随机化检验在弱零假设下的性质。文献[83-85]提出通过反转一系列随机化检验,以构建准确的置信空间。文献[86]从缺失数据的角度讨论了不同的统计推断框架。
8. 观察性研究中的工具变量和阴性对照方法
在很多科学研究中,人们最终的目的是评价一种处理或者暴露因素对一种结果或者响应变量的因果作用。自文献[75]提出随机化试验以来,其成为一种非常有效和广泛使用的评价因果作用的方法。但是,在很多研究中,由于伦理、经济或者不依从因素的制约,随机化试验并不适用或者代价太高;反而,在这样的研究中,观察性研究提供了更重要的数据来源和研究方法。不过,在观察性研究中,推断因果作用仍然面临很多挑战。最常见的问题是有混杂因素存在。混杂因素是指同时影响关心的处理和结果的因素或协变量。如果混杂因素被观测到,可以使用标准的统计推断方法做调整。然而,如果有混杂因素未被观测到,这些标准的调整方法通常失效,甚至会导致悖论。著名的Yule-Simpson悖论[19,20]就是一个例子。关于混杂的概念,文献[87,88]提供了很好的文献回顾。关于已观测混杂因素的调整,文献[2,89,90]讨论了常用的调整方法,例如,倾向得分和逆概率加权,回归调整和双稳健方法。本文着重回顾两种针对未观测混杂因素的调整方法,一种是经典的工具变量方法;另一种是近期引起人们重视的阴性对照方法。本文使用X和Y分别表示关心的处理和结果变量,U是未观测的混杂变量。为了符号上的方便,忽略已观测的混杂变量,当然,本文的结果在条件为已观测的混杂变量时仍然成立。使用小写的英文字母表示相应变量的一个观测值,例如,y表示Y的一个观测值。
工具变量方法在1928年由文献[91,92]提出,现在,该方法已成为经济学、社会学、流行病和生物医学等学科中的观察性研究的重要方法。除了关心的处理和结果变量,这种方法还需要额外观测一个工具变量,用Z表示,其需要满足如下条件:
(1)Z对Y没有作用:Z⊥Y | (X, U)(无直接作用);
(2)Z和U独立:Z ⊥U(独立性);
(3)Z和X相关:Z ⊥X(相关性)。
即使在这三个假定下,也只能得到X对Y的因果作用的上下界,而不能唯一确定因果作用,也就是不能识别[93,94]。为了识别因果作用,需要额外的信息或者模型假定。结构方程模型[91,95]和结构均值模型[96]是常用的模型。这两个模型通过假定因果作用的同质性,即在不同个体上的因果作用是常数,从而得到识别性[97]。一个例子是常见的线性模型(Y|X, U) = α + βX +U,实际上假定了在所有个体上的因果作用都是β;根据这个模型可以得到人们熟知的工具变量识别公式βiv= σsy/σxs。除了同质性的模型假定,在一些实际问题中可以假定单调性。例如,在一些临床试验中,Z表示处理分配,X表示个体实际接受或者采取的处理,由于有不依从存在,X可能和Z不完全相同,但是有时可以合理地假设Z对X的作用是单调的:Xz=1≥ Xz=0,即没有个体会采取与其被分配的相反的处理。这里,XZ表示在处理分配Z = z下潜在接受的处理。在单调性假定下,可以识别依从组的因果作用:(CACE) = E(Y1-Y0|X1= 1, X0= 0) [98]。此外,在一些应用场景,比如统计遗传学中,当有多个或高维工具变量时,如何选择工具变量变得很重要[99,100]。
在实际研究中,寻找一个满足如上三条工具变量假定的变量并不容易,而且工具变量方法对这三条假定都非常敏感。如何验证工具变量假定也是一个重要话题,例如,使用工具变量不等式做检验,见文献[94,101]。如果工具变量假定不成立,因果作用通常不可识别,工具变量方法也有偏,在这种情况下,求因果作用的界和敏感性分析方法更加稳健[102,103]。
由文献[104-106]提出和建立的基于阴性对照的因果推断方法提供了一个新的观察性研究的工具,也提供了一个补救工具变量可能失效的方法。阴性对照变量分为两类:阴性对照结果和阴性对照暴露,分别用W和Z表示,它们分别是一个辅助的结果变量和暴露变量,分别需要满足如下的条件:
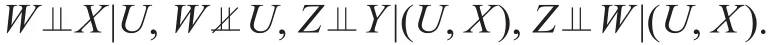
阴性对照暴露Z可以看作工具变量的推广,其满足对Y无直接作用的假定,但不必和未观测的混杂U独立,这一点不同于工具变量。给定一对阴性对照暴露和结果变量,在一定的正则性条件下,文献[104,106]证明了平均因果作用的非参数识别性,即不需要假定参数化的模型。这里,作为示例,考虑线性模型E(Y |X, U) = α +βX +U,并假定E(W|U)也是关于U的线性模型,那么,β的阴性对照识别结果为:
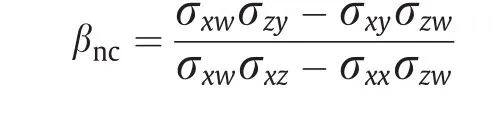
这个识别公式也适用于是工具变量的情况,因为,如果Z是一个工具变量,那么Z⊥U且σzw= 0。因此,工具变量方法可以看作阴性对照方法的特例,当Z不满足工具变量的假定时,使用阴性对照结果W来消除Z造成的偏差。但是,阴性对照比工具变量需要的假定更弱,在实际中例子很多。例如,文献[107,108]回顾了观察性研究中的许多阴性对照的实例;文献[105,109]还指出,在很多时间序列研究中,阴性对照成立。例如,在空气污染研究中,当前时间的空气污染不影响前一段时间的公共卫生状况,而后一段时间的空气污染也不影响当前时间的公共卫生状况,即公共卫生状况对空气污染没有反馈作用。在这种情况下,前一段时间的公共卫生状况和后一段时间的空气污染可以分别作为阴性对照结果和阴性对照暴露变量。
文献[104-106]提出的阴性对照方法需要两个阴性对照变量,当只有一个阴性对照结果或者一个阴性对照暴露时,因果作用不可识别。
在这种情况下,文献[107,109,110]研究了使用单个阴性对照检验混杂是否存在和减小偏差的方法,但不能识别因果作用。当阴性对照变量很多时,文献[111,112]通过因子分析的方法消除偏差,但需要依赖严苛的参数化模型假定。
总之,观察性研究中如何处理混杂因素仍然是一个难题。尽管使用工具变量和阴性对照等辅助变量方法可以大幅提高因果作用的识别性,但是工具变量和阴性对照的假定不能通过观察数据检验,而需要先验知识或者额外的研究确认。把先验知识和观察数据结合起来推断因果作用是观察性研究的一个可行的方向。现代大数据为因果推断提供了非常广阔的研究场景,但是,大数据通常都是观察性数据,而不是试验数据。因此,在大数据研究中处理混杂因素很重要。如何把先验知识和大数据结合起来更有效地推断因果作用需要更深入的研究。
9. 有干扰下的因果推断
个体处理稳定性假设是传统的潜在结果模型中的一个重要假设,它假设个体之间是没有干扰的[76]。但是,在很多试验和观测性研究中,个体之间会相互影响,从而造成了个体间的干扰。例如,在教育学或者社会学研究中,参与培训计划的学生会通过课堂外的交流影响没有参与的学生[113,114]。在流行病学中,传染病的预防措施会使得人们被传染的概率降低,因此即便没有接受预防的人群也会受到影响[115,116]。在这些研究中,个体接受到的处理不仅会对自己的结果变量有直接作用,还会对其他个体的结果变量有溢出作用。在实际问题中,直接作用和溢出作用有着重要的科学意义和社会意义,它们能帮助我们更好地理解因果作用的机制,从而能对政策或者方案的实施有指导作用。
在干扰存在的时候,一个个体的潜在结果的数量会随着整个样本中个体的数量呈指数增长。因此,在对干扰的结构没有约束时,我们无法得到直接和溢出作用的估计。有许多文献对干扰下的因果作用的估计进行了研究[117],其中一个重要的方向是将干扰限制在一些不重叠的小群体中,假设不同群体之间的个体没有干扰[52,114,118-122]。这种假定被称为部分干扰假定[114]。近来,许多研究者试着减弱这个假定去处理更一般的干扰结构[123-126]。在有干扰的情况下,因果作用的方差估计会变得更加困难。文献[118]指出,即便在部分干扰假定下,直接和溢出作用的估计依然是很困难的。在不加任何模型假设的条件下,一个能得到有效的方差估计的方法是假设个体的结果变量只依赖于自己接受到的处理和其他个体接收到的处理的某个函数。例如,个体的结果只依赖于自己是否接受了处理,以及有多少个其他个体接收到了处理。
另外一个方向的研究侧重于如何根据干扰的结构去设计试验估计因果作用。在部分干扰的假定下,文献[118]提出两阶段随机化试验去估计直接和溢出作用。在更复杂的干扰结构下,研究者提出了各种各样的试验设计去得到因果作用的点估计和方差估计[127-129]。
对于干扰情况下的统计推断,文献[130,131]依赖于关于潜在结果的模型,文献[79]对没有溢出作用的零假设提出了一个条件随机化检验的方法。文献[80]将这个方法推广到了一大类关于焦点个体的假设检验中。基于这些方法,文献[132]提出了得到有效的条件检验的一般程序。
虽然研究者对个体间的干扰提出了许多方法,但是这方面的研究依然存在着很多挑战。首先,个体干扰下的极限性质还不够完善。文献[133]研究了均值差估计量在有限制的干扰假定下的一致性。文献[134]在部分干扰假定和分层干扰的假定下得到了直接作用和溢出作用的中心极限定理。但是在一般的干扰结构下,即便是最简单的均值差估计量,极限性质都是不清楚的。其次,在有复杂数据时,个体间的干扰会变得更加难以处理。文献[120,121,135,136]考虑了干扰情况下的不依从问题,文献[137]研究了干扰情况下生存时间数据的分析方法。但是,对于其他类型的复杂数据,比如缺失数据和测量误差还没有方法来进行处理。最后,绝大部分的文献关心的是直接作用和溢出作用,但是个体间的干扰在其他的问题中也会存在,比如中介分析(见文献[138])和纵向数据分析。在这些问题中,我们关心的因果作用是不一样的。因此,我们需要将这些问题中的一些常用方法进行推广去处理个体间的干扰。
Compliance with ethics guidelines
Kun Kuang, Lian Li, Zhi Geng, Lei Xu, Kun Zhang,Beishui Liao, Huaxin Huang, Peng Ding, Wang Miao, and Zhichao Jiang declare that they have no conflict of interest or financial conflicts to disclose.

