多序列比对算法族的形式化设计与生成*

张旭初，石海鹤

(江西师范大学计算机信息工程学院，江西 南昌 330022)

1 引言

高通量测序技术[1]的飞速发展推进了国际上众多基因组计划[2]的实施，生物信息学[3]领域生成了海量的数据，促使生物信息大数据逐渐形成，且规模还在不断增长。目前生物信息学面临的一大挑战就是如何快速准确地分析这些数据，序列比对是对生物序列数据进行研究的基本途径和方法[4]，其原理符合生物学中的相关化学基础。

多序列比对是序列比对的重要组成部分，在序列信息分析、蛋白质功能分析、测序数据的基因纠错等方面应用广泛。多序列比对结果往往为相关的生物学研究提供基础或依据，其算法的性能至关重要。多序列比对结果的准确程度在于它是否可以尽可能准确地显示相关的生物学意义，为了量化这一标准，直观地评判多序列比对结果的优劣，研究人员引入了目标函数这一数学模型。比对和函数[5]是目前被广泛认可的目标函数，它的理论基础是得分函数具有可加性，通过双序列比对得分和来评估多序列比对结果。后续研究人员提出了准确性更高的一致性函数[6]，它反映了比对结果和双序列比对扩展库之间的一致性程度。基于相关目标函数的多序列比对问题已被证明是NP难题[7]，因此研究人员只能致力于寻找该问题的近似最优解。在目标函数的研究中，相关参数的优化选择也是一个重点[8]，实际应用时，合适的目标函数选择与合适的参数设置可以大大提高多序列比对算法结果的质量。

多序列比对算法主要有精准比对算法和近似比对算法。然而，精准比对算法由于其对计算机资源的消耗过高，无法应用于实际研究，不予赘述。近似比对算法为了降低多序列比对问题的复杂性，对比对结果的准确性进行了妥协，主要包括启发式比对算法和随机概率型比对算法等。启发式比对算法主要包括渐进式比对算法[9]和迭代比对算法[10]。渐进式比对算法思想于1987年由Feng等人提出，他们认为参与多序列比对的序列之间存在一定的进化关系，可沿着进化关系对序列进行逐步比对，直至所有的序列都比对完成。因此，在进行渐进式比对之前，如何寻找隐含在序列组中的进化顺序至关重要。1994年，Thompson等人[11]实现了渐进式比对算法思想，提出了ClustalW算法。渐进式多序列比对算法的主要缺点在于它的“一旦空位，永远空位”原则，比对过程中产生的错误会一直影响序列比对过程，以致算法难以获得比对问题的近似最优解，降低了算法精度，更无法处理大规模数据。2005年，Lassmann等人[12]运用Wu-Manber近似字符串匹配算法优化了距离矩阵的计算与渐进式比对的操作，进而提出了Kalign算法，它在数据量较大和距离较远的序列比对中更准确，消耗时间更短，该算法还在不断改进以适应数据量剧增的多序列比对需求[13]。此外，研究人员还提出了通过寻找中心序列来进行渐进式比对的HAlign算法[14]。目前研究人员主要使用迭代思想和一致性函数2种策略来优化渐进式比对。2000年，Notredame等人[15]提出的T-COFFEE算法，就是利用一致性函数对渐进式比对算法进行了优化，提高了比对结果的质量，但增加了比对时间。迭代比对思想运用可快速生成比对的算法，在产生初步比对结果后，通过相应的迭代操作来改进，直到比对结果不再优化或是已达到既定迭代次数为止。利用迭代比对思想，可以提高渐进式比对算法的鲁棒性，优化渐进式比对前期错误无法改进的缺陷，同时也扩宽了算法的适用范围，这类算法常见的有MAFFT[16]、MUSCLE[17]等。除此之外，通过随机概率算法如蚁群算法[18]、隐马尔可夫模型[19]、人工蜂群算法[20]等来进行迭代比对也取得了较好的成果。

由于双序列比对可对序列之间的相似性进行刻画，因此常被用于辅助多序列比对。Needleman-Wunsch算法[21]是最经典的全局双序列比对算法，而Smith-Waterman算法[22]则用于解决局部双序列比对问题，它们均基于动态规划思想。然而，标准动态规划算法在处理序列组的两两比对时，内存空间占用过大，时间复杂度较高，后续出现了优化空间复杂度的Hirschberg算法[23]、快速序列联配FA(Fast Alignment)算法[24]和优化的全局双序列比对OGP(Optimized Global Pairwise)算法[25]等。在对结果准确性要求不高的情况下，可以采用启发式近似比对算法来处理较长序列的比对，这一类算法包括FASTA[26]、BLAST[27]、MUMmer[28]和AVID[29]等，其中前两者主要用于参考基因组的相似性序列搜索。

在生物信息学的研究中，分析物种的进化历史、确认各个物种之间的亲缘关系也是一个热点问题。构建系统发生树(Phylogenetic Tree)可以直观地展现物种之间的进化关系和进化距离。同时，在多序列比对算法中，系统发生树也可作为指导树来指导比对操作。建立系统发生树主要有3种方法：距离矩阵法[30]、最大简约法[31]和最大似然法[32]。距离矩阵法是目前最常用的方法，它根据序列间两两比对的结果经过相应的计算建立距离矩阵，然后用聚类算法根据距离矩阵构造系统发生树。计算距离的方式决定着系统发生树的质量，而序列距离的计算通常受到遗传模型的影响。

目前，多序列比对算法族MSAA(Multiple Sequence Alignment Algorithm)的研究主要集中在特定算法特定步骤上的优化[33,34]，或是对算法进行并行化实现[35]，算法的比对效率和准确性提升对不同序列产生的优化效果有所不同。由于多序列比对算法的种类多样性和结构复杂性，许多使用者无法恰当选择符合序列特点的算法，在应用过程中可能产生不必要的误差。因此，从领域抽象层次对多序列比对算法开展研究极为必要。通过分析和提取MSAA领域的共性和异性，形式化构建算法理论框架，进而生成特定的MSAA领域算法，将有助于提高MSAA领域算法的可靠性和开发效率。

本文后续在已有工作的基础上对MSAA的形式化设计与生成进行阐述。相关的理论与方法学主要是领域工程、形式化方法PAR(Partition-And-Recur)[36 - 41]和产生式编程GP(Generative Programming)[42]等。基于产生式编程思想，运用面向特征的领域建模方法FODM(Feature-Oriented Domain Model)[43]对MSAA算法族进行领域分析，建立MSAA领域特征模型，并设计相应的算法生成架构与构件交互模型。进一步运用PAR予以形式化实现，从而建立Apla高抽象构件库，将Apla构件进行组装并转换，生成可执行的算法，最后运用实际的DNA序列对生成的算法进行实验分析。

2 相关方法

2.1 领域工程

领域工程[44]是软件复用的基础过程，它的目的是在某一特定领域中获取并运用可重用资源，高效、低成本地开发高质量的软件。领域工程主要对领域进行分析、设计与实现。领域分析包括系统范围界定、领域需求定义、相关术语分析等一系列活动，最终将结果都反映在领域模型中。领域设计完成了领域中系统族的架构设计，识别了相应的功能以及相关的约束条件，除此之外还对后续实现过程制定了计划。领域实现运用合适的技术完成对架构、组件等可复用资源的开发。这3个阶段在实际应用时采用逐步求精的思想，随时根据需求的变化对已完成的成果进行修改和完善。

领域分析是领域工程的基础，所生成的领域模型影响后续工作的质量，通常采用自顶向下和自底向上结合的方式，反复进行领域分析活动。自顶向下分析考虑较多的是领域中未来系统所要满足的需求，自底向上分析则较多考虑目前已有的系统以及之前开发所积累的可复用资源。为了高效地进行领域分析活动，张伟等人[43]提出了一种特征建模方法FODM，该方法重点考虑了领域中的服务、功能和行为特点等特征，论述了一种特征模型的展现形式及其详细建模过程。

2.2 PAR

PAR[36]包括一种切实可行的形式化方法以及相应的支持平台。PAR平台包括需求设计语言SNL(Structured Natural Language)、算法建模语言Radl、抽象程序设计语言Apla、一系列转换规则及自动转换工具。PAR注重于算法的设计与实现，支持目前主流的大多数算法设计技术，包含新式的循环不变式开发策略，实现了分布式事务处理系统以及关系数据库机制。运用PAR方法开发算法，可以对算法有更深刻的理解，避免产生对设计方法的选择困难问题。敏捷的泛型机制是PAR的重要特性之一，无论数据类型、数据值、计算操作还是用户自定义ADT(Abstract Data Type)均可以是泛型参数。Apla可以直接使用抽象数据类型和抽象过程编写程序，它既有数学语言简洁的优点，也有表达无歧义的特点，其语言本身的高抽象性，十分适合描述抽象算法程序。下面介绍一下Apla泛型的实现机制与约束机制。

(1)Apla包括类型变量、类型域、操作变量、操作域、ADT变量和ADT域的概念，分别使用sometype、someaction和someadt表示类型域、操作域和ADT域，实现了类型、函数、程序、自定义ADT等的参数化操作。实例化过程中可传入符合相关属性条件的实参来实现不同的程序单元。

(2)泛型约束详细描述了泛型参数的类型和构成，泛型约束机制的实现可大大提高泛型程序的可靠性，是真正实现泛型编程的必要条件之一。PAR平台对基本数据类型、ADT类型、子程序类型等泛型参数实现了相关泛型约束，提出了相应的约束描述、匹配和检测机制，且仍在不断的完善中[45]。

除此之外，PAR平台还支持将Apla转换为C++、Java、C#、Delphi等可执行的高级程序设计语言，对于构件的开发有着较好的支持。PAR建立了2条形式化开发程序的途径，其平台架构如图1所示。第1条是对于量化问题而言，PAR方法可以将SNL需求模型转换为Radl规约模型，继而转换为Radl算法模型，再进一步转换为Apla抽象程序模型，最后转换为可直接运行的高级语言程序。第2条途径是对于非量化问题，可以直接通过SNL需求模型手工设计Apla程序，并辅以相应的形式化证明，再将Apla程序转换为可执行程序。

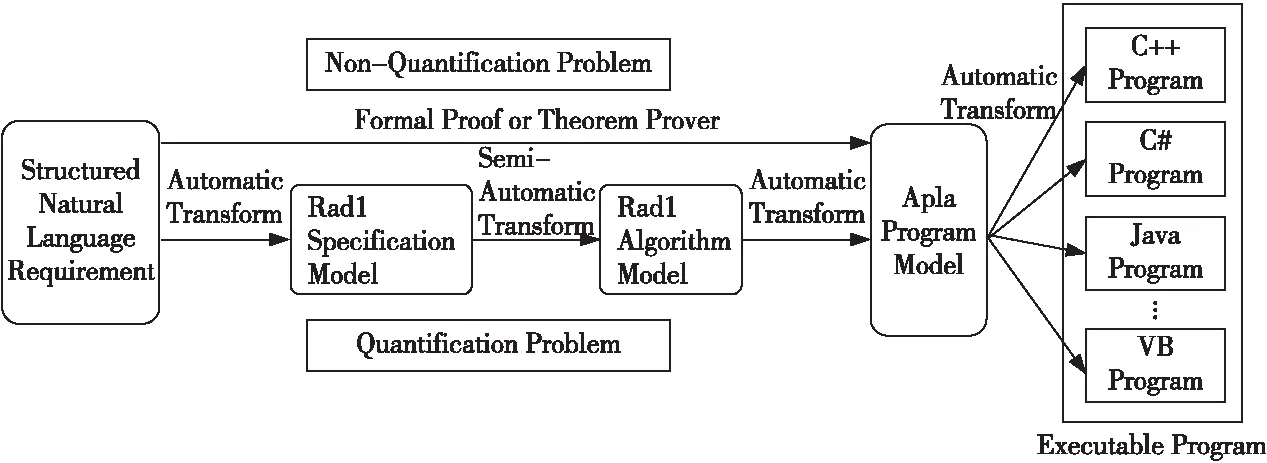
Figure 1 Architecture of PAR platform图1 PAR平台架构

2.3 产生式编程

产生式编程GP是一种新型的软件范型，符合软件复用的思想，使用组件并以一种自动化的方式来制作软件产品，对解决“软件危机”有重要的意义。实现GP要经过2个步骤。首先是将目前的软件开发模式转变为对软件系统族的开发，然后还需要开发产生器来对组件进行自动装配。GP是领域工程运用的一个实例，它需要充分利用现有的领域知识完成相应领域的构件开发，最终利用产生器通过构件装配的方式开发领域中的新软件，无需按照软件工程的步骤从头开始编程。

产生式编程的目的是实现对组件和应用程序的生产自动化，其关键的部分是对系统族建立领域模型。产生式领域模型包含3部分：问题空间、解空间和相应的配置知识。问题空间中主要包括应用程序员和用户对系统的需求，需求一般利用程序的概念和特征进行描述；解空间包括可以解决需求问题的相关组件以及各组件的组合模式，并要求达到最大的可组合性，且组合间的冗余要达到最小，还必须尽可能实现组件的最高重用性。配置知识则是问题空间与解空间的映射关系，避免了非法特征组合的出现，且对特征的默认参数与规则进行了设置。

3 MSAA建模

3.1 领域分析过程

本节建立在对目前常用的多序列比对算法研究的基础上，对先前的研究结果进行扩展[46]，利用FODM的建模方法对MSAA领域中的服务S(Service)、功能F(Function)、行为特点B(Behavior characteristics)进行特征建模。 多序列比对服务是MSAA领域的核心服务，该领域中的主要功能有双序列比对算法PSAA(Pairwise Sequence Alignment Algorithm)操作、系统发生树算法PTA(Phylogenetic Tree Algorithm)操作、启发式多序列比对算法HMSAA(Heuristic Multiple Sequence Alignment Algorithm)操作以及目标函数OF(Objective Function)评价。其中双序列比对算法操作、系统发生树算法操作为可选择功能，目标函数评价和启发式多序列比对算法操作是必选功能，对每个功能的描述仅关注主要组成部分。动态规划比对(DP)和快速比对(fast)是双序列比对算法操作的子功能，对于动态规划比对，动态规划模式选择(DP_mode)是其行为特点， 主要包括2种模式可供选择：标准动态规划算法(normal)和优化内存消耗的动态规划算法(space_opti)。距离法(dist)、最大似然法ML(Maximum Likelihood)和最大简约法MP(Maximum Parsimony)是系统发生树算法操作的子功能，对于距离法和最大似然法，遗传模型选择(genetic_model)是其行为特点， 这里只显示了2种常用的遗传模型，分别是kimura两参数模型(kimura)和Judes-Cantor单参数模型(JC)。对于距离法，它还有一个行为特点 是对聚类算法的选择(dist_algorithm)， 聚类算法的选择模式主要有2种：邻接法NJ(Neighbor-Joining method)和非加权配对算术平均法UPGMA(Unweighted Pair-Group Method with Arithmetic means)。启发式比对算法操作主要包括2个子功能，渐进式比对(prog)在之前的研究中已进行详细叙述，对于迭代比对(iter)，迭代模式选择(iter_mode)是其行为特点， 且存在多种模式可供选择，图2中只显示了迭代渐进式比对(progIter)和基于隐马尔可夫模型(hidden Markov)的迭代模式。对于目标函数(OF)评价，目标函数选择(OF_sel)是其行为特点 ，包括一致性函数(COFFEE)和比对和函数(SP) 2种函数选择模式，除此之外，目标函数计算参数设置(para_set)也是其行为特点， 且需要同时设置2种参数：罚分模型(penalty)和替换矩阵(subMatrix) 。MSAA领域的特征模型如图2所示。

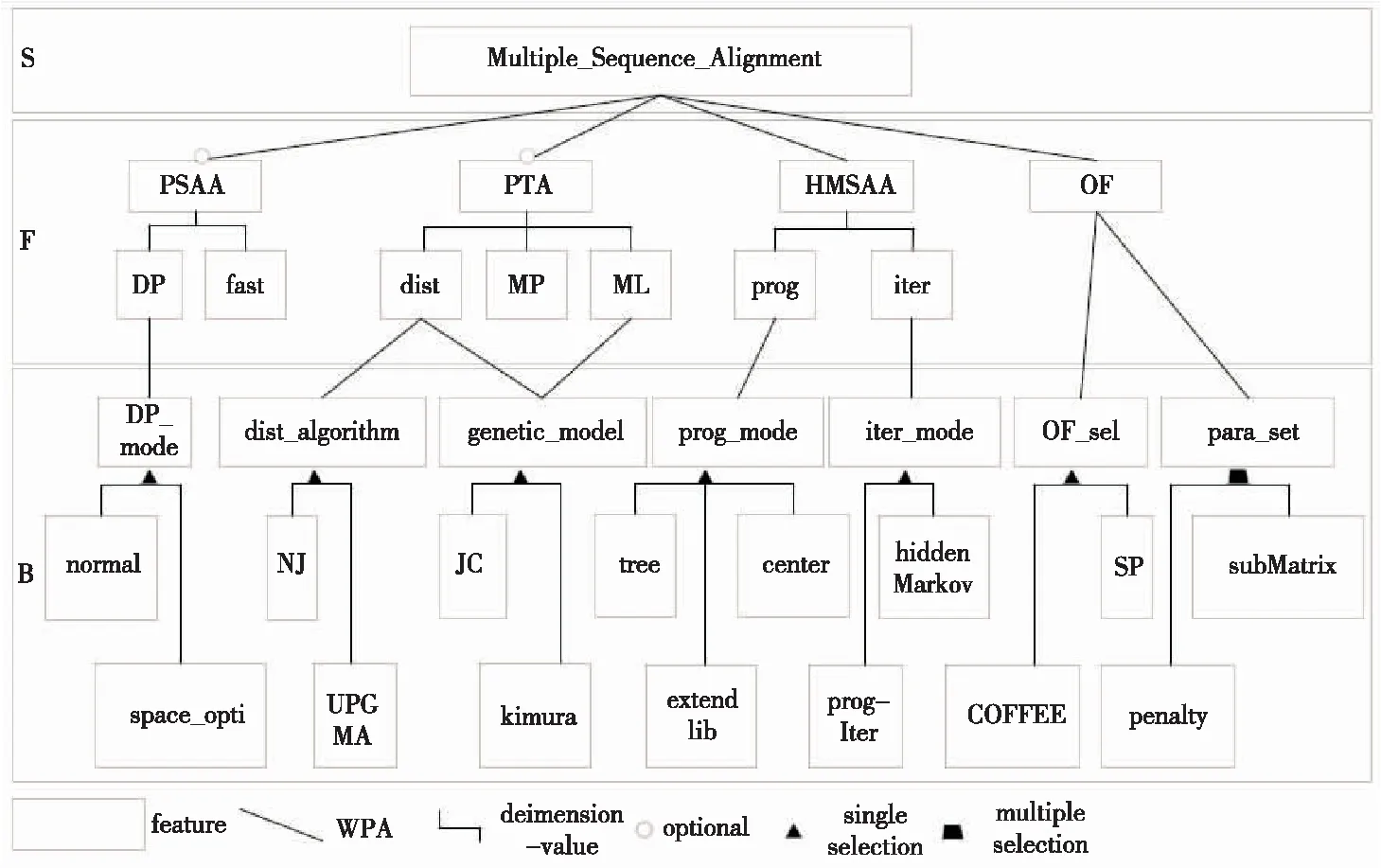
Figure 2 Feature model of MSAA图2 MSAA特征建模

3.2 领域设计过程

对多序列比对算法进一步分析后，得出3种常见的渐进式比对算法步骤，如图3所示。3种多序列比对算法有共同的起点与终点，均需进行双序列比对以及最后确定最佳渐进式比对的操作，不同之处在于根据系统发生树或星比对确定比对顺序的算法通常采用SP目标函数，而采用COFFEE目标函数的算法，则一般是通过双序列比对信息构建拓展库以指导多序列比对。 迭代比对中常用的是MUSCLE算法，其思想是将渐进式树比对算法进行迭代，在每一个子步骤中，选择执行速度更快的方法，例如运用k-mer算法[47]来进行双序列比对。进一步通过迭代思想提高多序列比对MSA(Multiple Sequence Alignment)的精度，其算法步骤如图4所示。在此基础上，可对迭代部分进行替换来产生其他新式的多序列比对算法。

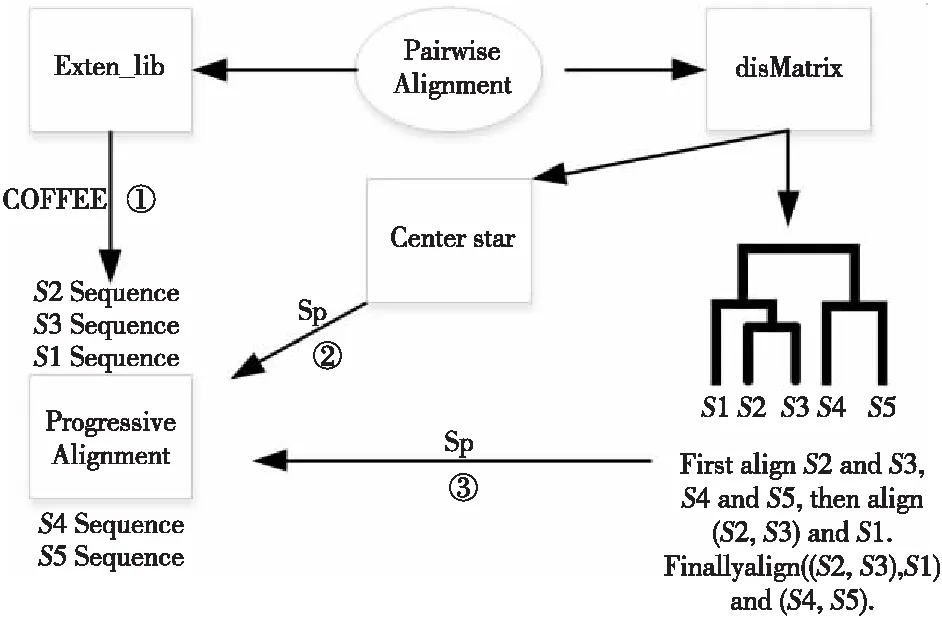
Figure 3 Steps of three common progressive alignment algorithms图3 3种常见渐进式比对算法的步骤

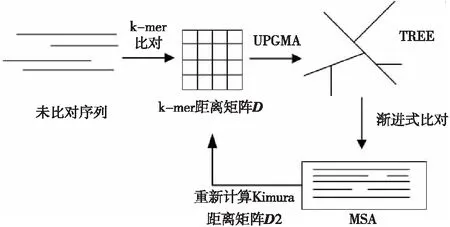
Figure 4 Steps of the MUSCLE图4 MUSCLE算法的步骤

通过上述分析，下一步根据MSAA领域的特征模型进行领域设计，对特征之间的约束以及依赖关系进行设计分析，建立算法构件的交互模型。本节仅对MSAA领域中渐进与迭代结合的多序列比对算法进行交互设计，以此做一个简单的示例。该领域算法的输入为生物信息序列，包括核酸序列或蛋白质序列，在算法执行前需要对序列信息进行合法性检查，检查输入序列中是否包含非法的碱基字符或氨基酸字符，因此该类型算法的主要构件为序列合法性检查构件(seq_check)、多序列比对模式选择构件(msa_mode)、启发式多序列比对算法(HMSAA)构件、目标函数(OF)构件、双序列比对算法(PSAA)构件、系统发生树算法(PTA)构件和结果输出构件(result_op)。根据构件间的依赖关系建立构件的交互模型，如图5所示。

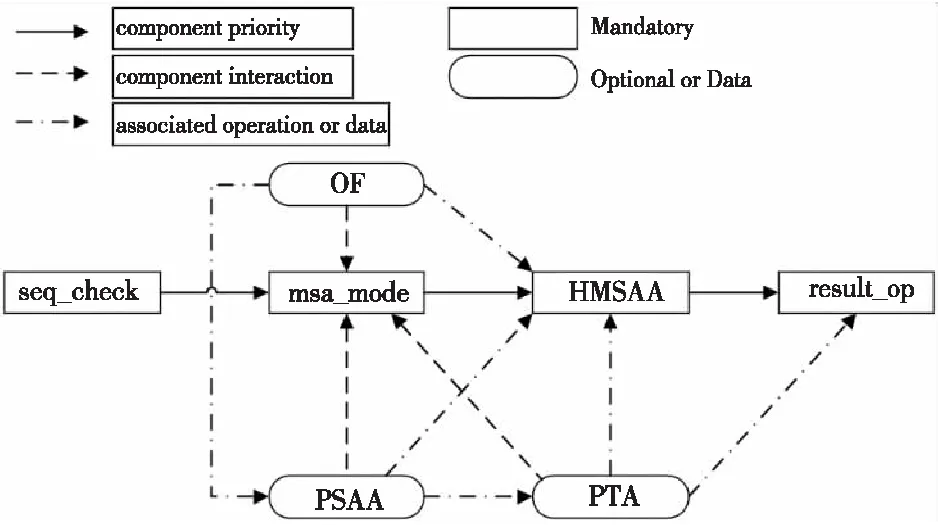
Figure 5 Interaction model of algorithm components图5 算法构件交互模型

图5中实线所连接的节点为迭代渐进比对中必须含有的基本构件，构件的执行优先级随着箭头方向逐渐降低。点划线箭头表示算法构件组装过程中所需的相关数据或操作，例如启发式多序列比对构件需要系统发生树构件的结果来指导后续比对。虚线箭头表示在算法执行过程中2个构件之间需进行交互，例如在选择算法类型时，多序列比对模式构件需调用OF构件、PSAA构件、PTA构件来进行装配操作。下面对关键构件进行了简单的形式化描述，采用自然语言的描述方式以便于理解该领域的算法构件。AQ和AR为Radl规约语言中定义的关键词，分别用于描述前置断言和后置断言。

(1)msa_mode构件。

|[inusersettingsoutmsa_mode: ADT]|

AQ: 用户已选择算法类型。

AR: 指定算法类型，并完成相应组装操作。

(2) PSAA构件[48]。

|[inOF: ADT;a[][]: Array[][];outb[][]: Array [][];score: double]|

AQ: 存在目标函数参数和需要进行比对的序列组。

AR: 序列两两比对的结果。

(3) HMSAA构件。

|[inOF: ADT;a[][]: Array[][];align: ADToutb[][]: Array [][]]|

AQ: 存在目标函数参数、需要进行比对的序列组以及比对所需的关联操作，具体由msa_mode指定。

AR: 比对结束的序列组。

(4) PTA 构件。

|[inPSAA: ADT;geneModel: ADToutphy_tree: ADT]|

AQ: 存在双序列比对产生的得分矩阵，并选择了相关遗传模型。

AR: 用以指导后续多序列比对操作的系统发生树。

4 Apla形式化实现及实验

本节根据MSAA领域的特征模型和算法构件交互模型，结合先前在HMSAA领域中的研究成果，对MSAA领域中的构件进行基于Apla的形式化实现。运用Apla中敏捷的泛型机制，提高算法的抽象性，在HMSAA领域构件的基础上进行符合约束条件的修改及扩展，扩大支持生成的算法领域范围。最后对生成的渐进式序列比对算法进行实验分析。

4.1 Apla实现

本节只展示迭代渐进比对算法的Apla组装实现，对先前的算法构件进行相应的修改。程序代码中仅列出了MSAA领域构件的定义，以及参数的具体释义。

(1)msa_mode构件。

该构件定义了一系列合法的泛型ADT组合，提高了算法的抽象性。泛型子程序msa根据用户在组装过程中传入的ADT，生成不同的多序列比对算法。

defineADTmsa_mode(sometypeelem);

proceduremsa(someadtadtset);

……

enddef

(2)HMSAA构件。

该构件被定义为ADT，主要包括2个泛型子程序，分别是渐进式比对Prog和迭代比对Iter，泛型子程序prog根据不同获取比对步骤的操作进行渐进式比对，泛型子程序iter包括迭代子算法IterNode，传入不同的迭代子算法操作，生成相应的多序列比对算法，flag表示迭代是否继续。

defineADTHMSAA(sometypeelem);

procedureprog(someactiongetSteps;seqs: array [string];seqsName: array[string]);

procedureiter(someactionIterNode;flag: boolean);

……

enddef

(3)PTA构件。

该构件定义为ADT，其主要用于进行系统发生树的计算操作。该ADT在运用距离法生成系统发生树时，需先调用dist_matrix中的泛型子程序DistMatrix，根据传入不同类型的双序列比对操作和遗传模型来计算序列组的距离矩阵。PTA构件中包括泛型子程序TreeByDist，它将selAl作为它的泛型参数，指定距离法中运用的聚合算法类型。

defineADTdist_matrix(sometypeelem);

procedureDistMatrix(someacationpsa;someactionselGm);

enddef;

defineADTPTA(sometypeelem);

procedureTreeByDist(distMat: elem;someactionselAlgorithm;seqName: array[string];first: Integer;last: Integer;treeName: string;result: boolean);

……

enddef

(4)OF构件。

该构件被定义为ADT，内部存储了使用仿射空位罚分所需的参数和替换矩阵，泛型子程序getOF定义了泛型操作参数comp，目前可运用Sp函数或COFFEE函数计算目标函数的值，用以评价多序列比对。

defineADTOF(sometypeelem);

gapOpen:double;

gapExtend:double;

subMatrix:array[array[double]];

proceduresetOFpara(gapOpen: double;gapExtend: double;subMatrix: array[array[double]]);

proceduregetOF(someactioncomp);

……

enddef

(5)result_op构件。

该构件被定义为ADT，泛型子程序multiAlign_op在多序列比对结果的基础上，对结果进行格式化输出，运用format泛型操作参数指定输出的格式化模式，常用的格式化模式有ClustalW格式、Phylip格式和Html格式等。子程序phyloTree_op将系统发生树结果进行输出。

defineADTresult_op(sometypeelem)

proceduremultiAlign_op(pathAlignOutput: String;ADTHMSAA; someactionformat);

procedurephyloTree_op(pathTreeOutput: String;seqName: array[string];ADTPTA);

enddef

根据构件装配形成迭代渐进式比对算法的装配代码如下所示。通过PAR平台的C++程序转换系统，可将Apla装配算法程序转换为可执行的C++程序。

programipmsa;

const/* input sequences*/

var

seqs,seqsName: array[String];

//seqs是待比对的序列组

//seqsName是比对序列对应的名称

seqsNum: Integer

//seqsNum是比对序列的条数

constpathTreeOutput: String;

constpathAlignOutput: String;

ADTpsa: newPSAA(dp_nw);

ADTdist: newdist_matrix(seqsNum);

ADTpta: newPTA();

ADThmsaa: newHMSAA();

ADTof: newOF(sp);

ADTresult: newresult_op();

of.setOFPara(gapOpen: double;gapExtend:

double;submatrix: array[array[double]]);

proceduredistMat: newdist.DistMatrix(psa,kimura，…);

proceduregenerateTree: newpta.TreeByDist(distMat,UPGMA,…);

procedureprog_align: newhmsaa.prog(tree,…);

procedureiter: newhmsaa.iter(prog_align,…);

ADTmode: newmsa_mode();

proceduremul_align_main(seqs: array[String];

seqsName: array[String];pathTreeOutput: String;

pathAlignOutput: String;ADTmsa_mode;ADTresult_op);//算法组装代码

var

res: Boolean;treeFileName: String;

begin

align_mode:mode;

result_type:result;

align_mode.msa(generateTree(distMat(…),…),of(…),iter(prog_align,…));

result_type.phyloTree_op(pathTreeOutput,seqsName,pta);

result_type.multiAlign_op(pathAlignOutput,ClustalW,…);

end;

procedureiter_prog_msa: newmul_align_main(mode,result,…);//主程序

begin

check(seqs);

iter_prog_msa(seqs,seqsName,seqsNum,…);

end;

4.2 实验

GenBank是由美国国家生物技术信息中心(NCBI)建立和维护的世界3大核酸数据库之一，本文从该数据库下载了4条关于血红蛋白或β球蛋白的DNA片段作为实验数据，四条序列的长度均在500个碱基以上。通过将组装形成的渐进式比对算法与ClustalO、MUSCLE进行实验比较，验证了目前已生成的算法具有一定的实用性。截取部分比对结果如图6所示，该图横线上半部分表示所生成的系统发生树结果，横线下半部分表示多序列比对结果。

Figure 6 Sequences alignment results图6 序列比对结果

5 结束语

近年来生物信息学发展迅速，但仍有大量问题未完全得到解决，多序列比对问题便是其中之一，由于其问题的NP完全性，研究人员试图寻求最佳近似解。现有的研究大多针对特定问题或特定算法，甚少从算法领域层次开展研究，存在着可重用性和开发效率较低、冗余性过高等问题，使用者往往难以选择恰当的多序列比对算法。

本文基于产生式编程思想和FODM的建模方法，考虑MSAA领域中的双序列比对、启发式多序列比对、系统发生树和目标函数等特征，通过一系列分析活动及回溯求精，构建了MSAA领域特征模型；深入分析特征间的依赖约束关系，抽取其中的通用特征以及可变特征，形式化设计了相应的算法构件及其交互模型，进一步使用PAR的Apla语言进行了形式化实现，建立了Apla泛型构件库；最后通过PAR平台的一系列程序转换系统将其快速装配生成可执行的算法。对比之前的研究结果，本文模型精化扩展了部分构件，提高了算法的抽象性与泛型程度，扩大了可组装算法的范围。

Apla语言的高抽象性与易于验证性，确保了构件装配算法的多样性，提高了算法构件库的可靠性；PAR平台自动或半自动的算法装配生成，提高了算法的开发效率，较好地展示了算法特征之间的关系，便于研究人员理解和使用算法。本文融合领域工程、产生式编程、形式化方法等理论、方法和技术在多序列比对算法族上开展的研究实践，理论上可为生物信息学中其他领域算法研究提供新的思路。

下一步工作将继续完善PAR和算法构件库，增加相应的算法构件，如隐马尔可夫模型，快速傅里叶变换等，将该方法学进一步应用于其他生物信息学研究领域中。同时也将积极开发可视化装配工具，方便算法构件的组装操作，用户通过选择不同的构件，即可生成相应的序列比对算法。运用XML文件对构件间的组成和约束关系进行刻画，装配操作只需修改XML文件的内容，而不会影响构件库中的组装代码。