体声波滤波器群时延波动的两种计算方法

袁 靖，高 杨，任万春

(1.西南科技大学 信息工程学院, 四川 绵阳 621010；2.西南科技大学 微系统中心, 四川 绵阳 621010)

0 引言

随着无线电技术的迅速发展和无线电设备应用领域的扩大，通信系统对滤波器性能提出了更高的要求[1]。与声表面波(SAW)滤波器和介质滤波器等相比，虽然体声波(BAW)滤波器具有体积小，品质因数(Q)值高及带外抑制好等优势，但也需要同时满足现代通信系统对BAW滤波器时域特性的高要求[2-4]。因为信号通过BAW滤波器后，BAW滤波器的非理想相频特性会使信号产生相位失真，这些失真会对通信系统的性能产生严重影响[5]。为了尽可能使带内信号通过BAW滤波器不失真，需要BAW滤波器有线性的相频特性，即BAW滤波器群时延波动尽可能小[6],因此需要对BAW滤波器群时延波动进行准确计算，以便根据计算结果对其性能进行评估和后续的改进。

BAW滤波器群时延波动表示为通带内群时延最大值和最小值的差。群时延可通过矢量网络分析仪测试后导出的S参数计算得到。为了从测得的S参数计算BAW滤波器群时延波动，本文分别给出了在ADS、MATLAB中计算BAW滤波器群时延波动的两种方法，并将一组测得的BAW滤波器的S2P文件分别导入ADS、MATLAB中进行计算，同时对两种方法进行对比，得到的结果基本吻合。

1 MATLAB中计算方法

1.1 S2P文件读取

首先需要创建一个m文件，m文件名和输入函数名一样都为“readS2P”；然后定义function函数和输入函数；接着找到S2P文件中数据开始存储的行；最后读取S2P中的每个频率点及对应的S参数的幅值和相位。S2P文件读取部分程序如下:

function [freq,S,magZ,angZ] =

readS2P(m,a,b)

fid = fopen(m);

tline = fgetl(fid);

i=0;j1=0;

while ischar(tline)%

if tline(1)==′!′

i=i+1;

j1=i;

elseif tline(1)==′#′

i=i+1;

else

break;

end

tline = fgetl(fid);

end

data=textread(m,″,′headerlines′,i);

freq=data([1∶1∶22000],1);

1.2 群时延波动计算

群时延波动计算同样应先创建m文件，m文件名和输入函数名一样都为“Filter_Measure”；然后定义function函数和输入函数；接着调用“readS2P”文件，并根据群时延的定义,编写群时延波动的计算程序。部分程序如下：

function [Daiwaiyizhi1]=Filter_Measure1(m)

[freq,S,Mag,Ang]=readS2P(m,2,1);

warning(′off′)

Ang=(Ang<0).*(Ang+360)+(Ang>0).*Ang;

AngPi=Ang/180*pi;

AngPi=AngPi(((freq<(2094+3.1)*1000000)&(freq>(2094-3.1)*1000000)));

oumiga=2*pi*freq;

oumiga=oumiga(((freq<(2094+3.1)*1000000)&(freq>(2094-3.1)*1000000)));

Qunyanshi=-diff(AngPi(1:1:end))./diff(oumiga(1:1:end))*10^9;

Qunyanshi1=max(Qunyanshi)-min(Qunyanshi);

str=[′....5.群时延波动=′num2str(Qunyanshi1)′ns....′];

disp(str);

end

1.3 数据输出

首先需要读取测试数据文件夹下所有测得的BAW滤波器的S2P文件；然后调用群时延的计算程序“Filter_Measure”文件；接着依此计算BAW滤波器的群时延波动；最后以excel形式输出计算数据。数据输出部分程序如下：

clc

clear

maindir = ′F:data高低温试验数据′;

subdir =dir(maindir);

for bianhao=[1 2 3 4 5 7 8]

Wendu=[];Qunyanshiall=[];

fori= 1:length(subdir)

filename=subdir(i).name;

flg=strfind(subdir(i).name,[′du_′num2str(bianhao)′#′]);

if(length(flg)～=0)

Wendu=[Wendu str2num(filename(1:flg-1))];

[Qunyanshi1]=Filter_Measure1(filename);

Qunyanshiall=[Qunyanshiall Qunyanshi1];

end

2 ADS计算方法

2.1 S2P文件读取

在ADS软件中计算BAW滤波器的群时延波动,首先在ADS软件中导入测得的BAW滤波器的S2P文件。具体方法是在ADS软件中新建一张原理图，然后放置S2P元件和相应的S参数端子，构成的电路图如图1所示。在S2P元件中导入测得的BAW滤波器S2P文件；S参数仿真设置的扫频范围和步长需要与矢量网络分析仪测量时保持一致。

图1 在ADS中导入S2P文件

2.2 “delay(S12)”计算群时延波动

在图1的基础上，双击“S-PARAMETERS”进入S参数仿真器设置中，选中计算“Group delay”；然后在ADS软件绘图框中的“Trace Expression”输入“delay(S12)”，得到BAW滤波器群时延频率曲线，如图2所示。

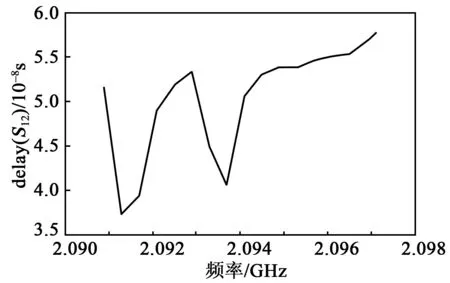
图2 “delay(S12)”计算群时延频率曲线

“delay(S12)”函数是利用群时延定义及下式计算[7]得到

(1)

式中:φ(ω)为相频特性曲线;ω为角频率;τ(ω)为群时延。

在ADS中仿真phase(S12)-频率曲线如图3所示。

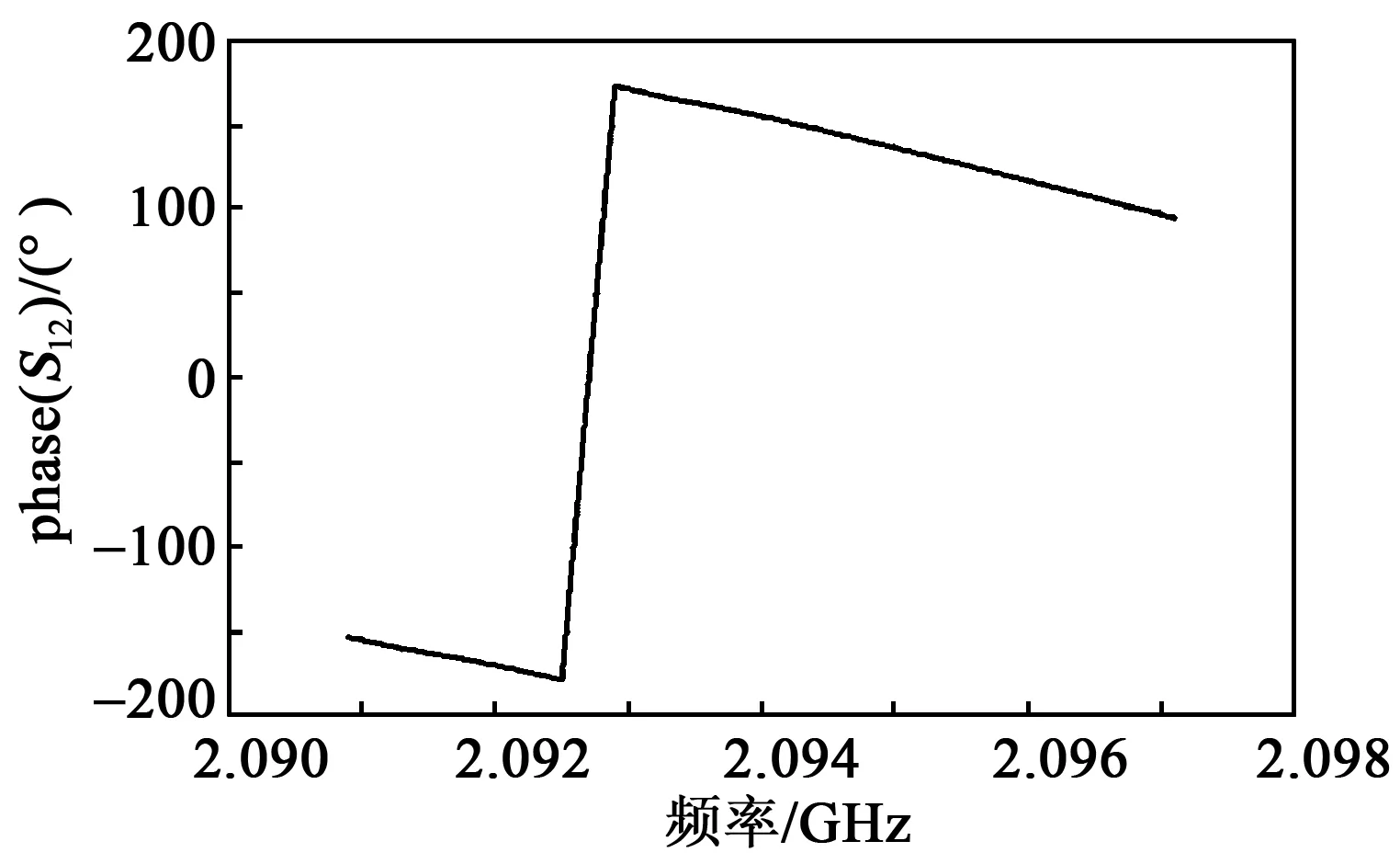
图3 phase(S12)-频率曲线

由图3可知，相位存在-180°～180°的跳变，这是因为计算一个系统相频特性时，要用到反正切函数提取相位，计算机中反正切函数规定，在一、二象限时角度为0°～180°，三、四象限时角度为0°～-180°。这使实际得到的结果发生相位跳变，跳变幅度为360°。群时延为相位变化量和频率变化量之比，相位发生跳变会使相位变化量增大，进而导致群时延增大。

2.3 “group_delay”计算群时延波动

为了避免“delay(S12)”计算时遇到的相位跳变问题，在ADS中可使用“group_delay”进行计算，即

group_delay=-diff(unwrap(phase(S12),π)/(2*π)

(2)

式中unwrap函数用于检查数据前、后两点的相位差距是否超过180°，超过为有跳变，后点的值自动减去360°。unwrap函数的作用是使相位在-180°处不发生跳变，从而反应出真实的相位变化，如图4所示。

图4 unwrap(phase(S12))-频率曲线

在ADS软件绘图框中的“Trace Expression”中输入式(2)，得到BAW滤波器群时延频率曲线如图5所示。通过计算带内群时延的最大值与最小值的差可得到群时延波动。

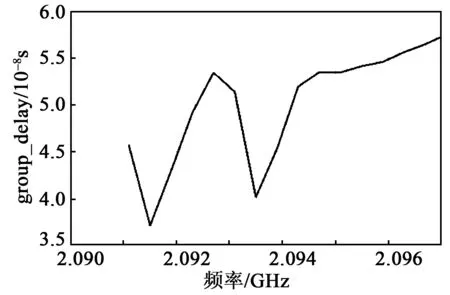
图5 “group_delay”计算群时延频率曲线

3 两种方法的算例对比

将用矢量网络分析仪实测的一个BAW滤波器S2P文件作为算例的输入数据，分别导入MATLAB、ADS中进行计算。一组S2P文件是BAW滤波器分别对8个温度点(-55 ℃、-30 ℃、0、+25 ℃、+50 ℃、+85 ℃、+100 ℃、+125 ℃)进行试验条件下测得。

BAW滤波器群时延波动在MATLAB中计算和ADS中使用“group_delay”计算的结果，如图6所示。

图6 MATLAB和ADS中使用“group_delay”计算的BAW滤波器带内群时延波动随温度的变化曲线

由图6可知，MATLAB计算和ADS使用“group_delay”计算的结果偏差≤0.8 ns,表明两种方法计算的结果基本吻合，均能正确计算BAW滤波器的群时延波动。

在ADS中分别使用“delay(S12)”和“group_delay”计算BAW滤波器群时延波动，其结果如图7所示。

图7 ADS中使用“group_delay”和“delay(S12)”计算的BAW滤波器带内群时延波动随温度的变化曲线

由图7可知，在ADS中使用“delay(S12)”计算时结果出错，这证实了相位跳变会导致计算的群时延波动偏大。

4 结论

1) 本文给出了在ADS、MATLAB中计算BAW滤波器群时延波动的两种方法。将一组测得的BAW滤波器的S2P文件分别导入ADS、MATLAB中进行计算，均能准确计算出BAW滤波器的群时延波动。

2) 在ADS中使用“delay(S12)”计算群时延波动时，因相位存在-180°～180°的跳变，当相位延时超过180°时会导致计算结果出错，因此需要使用增加unwrap函数的“group_delay”进行计算，以避免因相位跳变而导致的计算出错。