压电陶瓷驱动器迟滞建模与自适应控制
王 舟,陈远晟,王 浩,黄勤斌
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
0 引言
随着精密制造和精密工程的快速发展,微米、纳米级的定位技术成为目前精密加工、生物医学、微电子等领域的关键性技术,如压电陶瓷管扫描器、微夹持等[1-2]。压电陶瓷驱动器是理想的微位移元件,具有位移特性好,体积小等优点,但压电材料固有的迟滞非线性特性给精密定位带来影响[3]。
目前,国内外学者对于压电陶瓷的迟滞特性做了大量研究,Xianfeng Song等[4]提出了一种改进的Preisach模型, 并引入了开环控制器以消除迟滞影响。 经典的Preisach迟滞模型以积分的形式来描述迟滞特性,并且此方法还可以通过采用时间导数校正技术来处理非恒定频率依赖性。于志亮等[5]提出一种改进的Prandtl-Ishlinskii(PI)滞后模型对压电陶瓷执行器的迟滞特性进行前馈逆补偿,将迟滞特性线性度误差减小到 1% 以内,实现线性化。
为了进一步减小压电陶瓷的迟滞非线性,Chaoui H等[6]提出了一种具有滞后和干扰估计的压电驱动器自适应控制策略。自适应控制法是基于Lyapunov 的自适应定律学习压电驱动器的逆模型。可有效的在反馈回路中使用自适应估计器来估计磁滞和干扰,减小跟踪控制误差。Zhang Guoqing等[7]研究了由广义PI模型描述的具有未知非平滑滞后的不确定非线性时滞系统的跟踪问题。基于最小学习参数(MLP)的自适应神经算法,保证跟踪误差收敛到零的小邻域内,并且闭环系统的所有状态都稳定。胡力等[8]提出了一种最小二乘法与径向神经网络相结合的建模方法,用最小二乘法对迟滞曲线进行多项式拟合,得到压电执行器的迟滞数学模型,在此基础上再用径向基函数(RBF)神经网络法对该模型进行优化。最后对建立的模型进行分析发现,用最小二乘法拟合的多项式数学模型,标准方差δ=0.059 02 μm,而利用RBF神经网络优化建模后的δ=0.016 04 μm,对迟滞曲线有较好的补偿效果。
在研究压电陶瓷的物理特性时,Ruderman等[9]探索了Maxwell-slip 模型的滞后阻尼特性。考虑到经典的线性粘滞阻尼和Stribeck效应,运用运动动力学分析了力-位移滞后的非线性阻尼,并分析Lyapunov稳态特性。在此基础上,得到模型参数并消除误差。 最后,描述了预滑动滞后摩擦响应于零速度附近的相关实验示例。Maxwell-slip模型是一种基于物理现象的迟滞模型,其具有参数少,结构简单的优点,但存在弹性滑块单元的参数耦合问题,所以只能用来描述对称迟滞曲线。虽然有一定程度的控制效果,但是在高频条件下,模型所得误差还是较大。
传统的Preisach模型、PI模型和Maxwell-slip模型的离线辨识在单一频率下有良好的辨识效果,本文在经典Maxwell-slip模型的基础上引入自适应控制算法,减小跟踪控制误差,所用参数更少且适用于更宽频率,对于环境干扰能进行自动辨识,使其能够对压电陶瓷驱动器的迟滞现象进行描述,并用于实际控制系统中。
1 Maxwell-slip模型
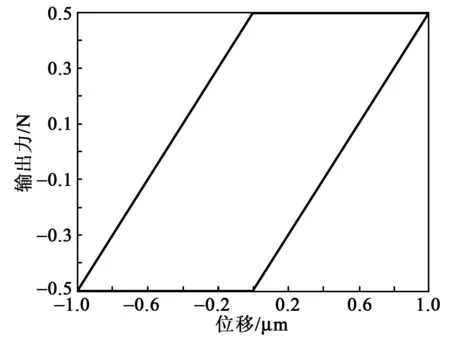
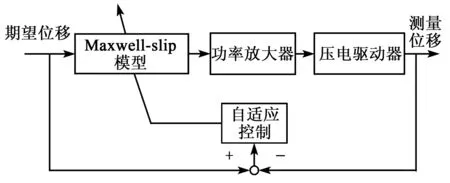
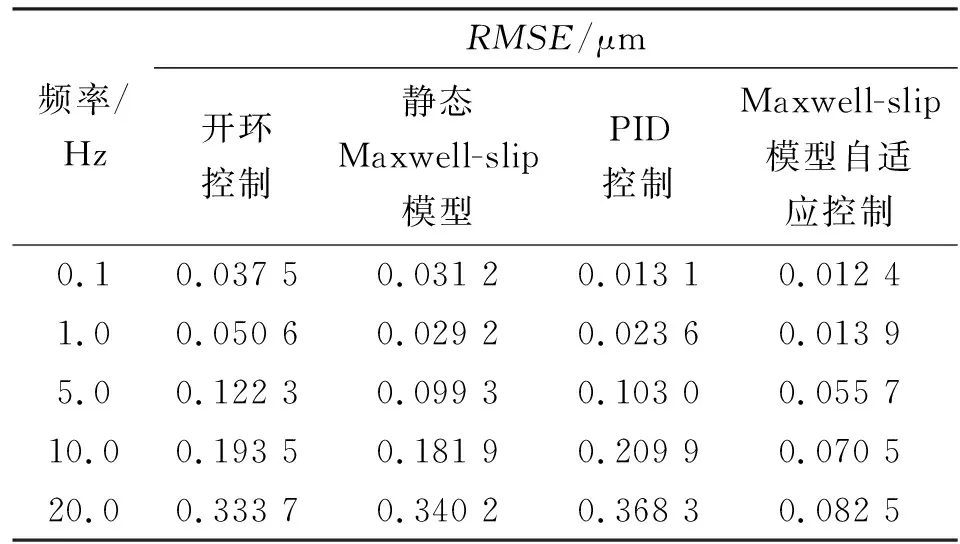
若|k(z-zi)| Fi=k(z-zi)zi不变 (1) 否则,滑块处于滑动状态,有 (2) 图1 Maxwell-slip模型 由式(1)、(2)可得到第i个单元输出力Fi,叠加到N个滑块单元后的整个系统预滑动阶段的输出力为 (3) Maxwell-slip模型的主要思想是: 假设摩擦力存在,当输入值足够大时,F与z的关系会出现迟滞现象,表现为平行四边形,如图2所示 。该弹簧阻尼系统的力与位移迟滞特性,与压电陶瓷驱动器的迟滞特性接近。另外,由于该弹簧的滑块无质量且处于并联状态,因此,增加N可无限逼近压电陶瓷迟滞特性曲线精度,却不增加模型的阶数。 图2 Maxwell-slip模型基础单元迟滞特性 若|k(z-zi)| (4) 否则,滑块处于滑动状态,有: (5) 式中wi为Fi的权值系数,叠加N个单元后的系统预滑动阶段的输出力为 (6) 图3为迟滞逆模型控制示意图。若模型精度足够高,则跟踪控制误差e(t)为 e(t)=v(t)-x(t)=v(t)-H[y](t)= (7) 式中:v(t)为Maxwell-slip模型的输入信号;x(t)为压电驱动器输出信号(Maxwell-slip模型的输出力即为压电的输出信号);y(t)为Maxwell-slip模型的输出信号和压电陶瓷驱动器的输入信号;H为Maxwell-slip模型的建立。 图3 Maxwell-slip模型控制系统示意图 神经网络在系统识别、信号处理等方面有广泛的应用,但它只能近似于一对一的映射[12-13]。为了模拟多值映射的滞后,提出了一种具有反激算子的神经网络。将反激算子引入神经网络的第一层,第一层的输出为 a1=H[wi·Fi(t)]=wi·H[Fi(t)] (8) 式中a1为第一层的输出向量。 反向传播算法是神经网络设计中最流行的训练算法之一[14-15],为了对所提出的控制算法进行参数辨识,引入文献[15]提出的神经网络中最后一层的敏感度公式,即 (9) 式(9)需要计算间隙算子的导数,H[wi·Fi(t)]是多值映射的非线性滞后函数,很难计算其导数,这使得训练算法和控制器设计复杂化。但与Maxwell-slip模型相似,由于每个单元的神经元传递函数是线性的,可以将式(9)作为最后一层进行线性迭代,那么wi将通过以下方式更新: (10) 式中:m为迭代次数;α为学习率;ai为第i层输出向量;s为式(8)的,神经网络中最后一层的敏感度,与每一时刻的位移误差有关。 为了验证Maxwell-slip模型的自适应控制算法的可用性与正确性,本文在LabVIEW软件上设计了迟滞控制模型进行实验验证。实验装置采用悬臂梁结构的压电控制平台,压电陶瓷双晶片采用嘉康公司生产的条形驱动器(51.7 mm×7.2 mm×0.83 mm),位移传感器采用IL-S025,位移分辨率1 mm对应1 mV,数据采集系统采用NI-compact RIO 9030系统,通过采集位移信号运算控制算法后,输出模拟信号-5~+5 V,实验装置如图4所示。实验输入信号选取0.1 Hz,1 Hz,5 Hz,10 Hz,20 Hz的正弦信号。经过Maxwell-slip模型自适应控制进行前馈补偿后,输入到压电双晶片后得到测量位移,Maxwell-slip模型自适应控制原理如图5所示。 图4 实验系统 图5 Maxwell-slip模型自适应控制原理图 根据上述实验方案进行测试,在压电实验平台上采集无前馈补偿控制下的测量位移,根据输入信号的期望位移与测量位移采集结果,可得到不同频率在无前馈补偿控制下的迟滞环。其中1 Hz、10 Hz、20 Hz下控制前的迟滞环如图6所示。 图6 不同频率下控制前的迟滞环 根据输入信号的期望位移与测量位移结果,可得到不同频率的Maxwell-slip模型自适应控制的迟滞环(见图7)。 图7 不同频率下的Maxwell-slip模型自适应控制迟滞环 本实验搭建悬臂梁结构的实验平台,压电双晶片驱动器共振频率较低,当压电双晶片远离共振频率时,控制效果较好,到达共振频率后,控制效果不理想。此模型与自适应控制法结合后,拓展了应用范围,在20 Hz下有一定控制效果。在本研究中,对比了在不同条件下3种控制方法的均方根误差(RMSE)和绝对值平均误差(MAE)的结果,如表1、2所示。控制方法分别为静态的Maxwell-slip模型,比例、积分、微分(PID)控制法和Maxwell-slip模型自适应控制法,并与控制前的控制误差进行对比。 表1 不同控制方法的RMSE结果 表2 不同控制方法的MAE结果 根据实验结果所示,静态Maxwell-slip模型仅在1 Hz辨识的静态权值下有一定的控制效果,当远离此频率,补偿控制效果不理想。PID控制在低频率(0.1 Hz、1 Hz)下有良好的控制效果,其中0.1 Hz频率下的RMSE降低到0.013 1 μm,随着频率的增大,跟踪控制误差也随之增大,RMSE的最大值达到0.368 3 μm。而对于Maxwell-slip模型自适应控制,在0.1~20 Hz宽频带下都具有良好的补偿控制效果,RMSE均未超过0.1 μm,说明Maxwell-slip模型引入自适应控制对压电陶瓷迟滞非线性在宽频带下有良好补偿控制效果。 本文采用一种改进的Maxwell-slip模型并引入自适应控制,对压电陶瓷驱动器的迟滞特性进行前馈逆补偿。在不同频率及不同控制方法情况下,对压电陶瓷驱动器线性度进行测试。实验结果表明,对于静态Maxwell-slip模型(经典模型)、PID控制和Maxwell-slip模型自适应控制在0.1 Hz下的控制效果接近。通过自适应控制的Maxwell-slip模型在20 Hz条件下控制效果更好,其均方根误差为0.082 μm,而其他两种控制的均方根误差分别为0.340 2 μm和0.368 3 μm,与经典模型相比,提高了压电陶瓷的控制精度和范围。有利于提高系统在宽频带下迟滞补偿效果,对于压电陶瓷驱动器在精密定位领域的研究有重要意义。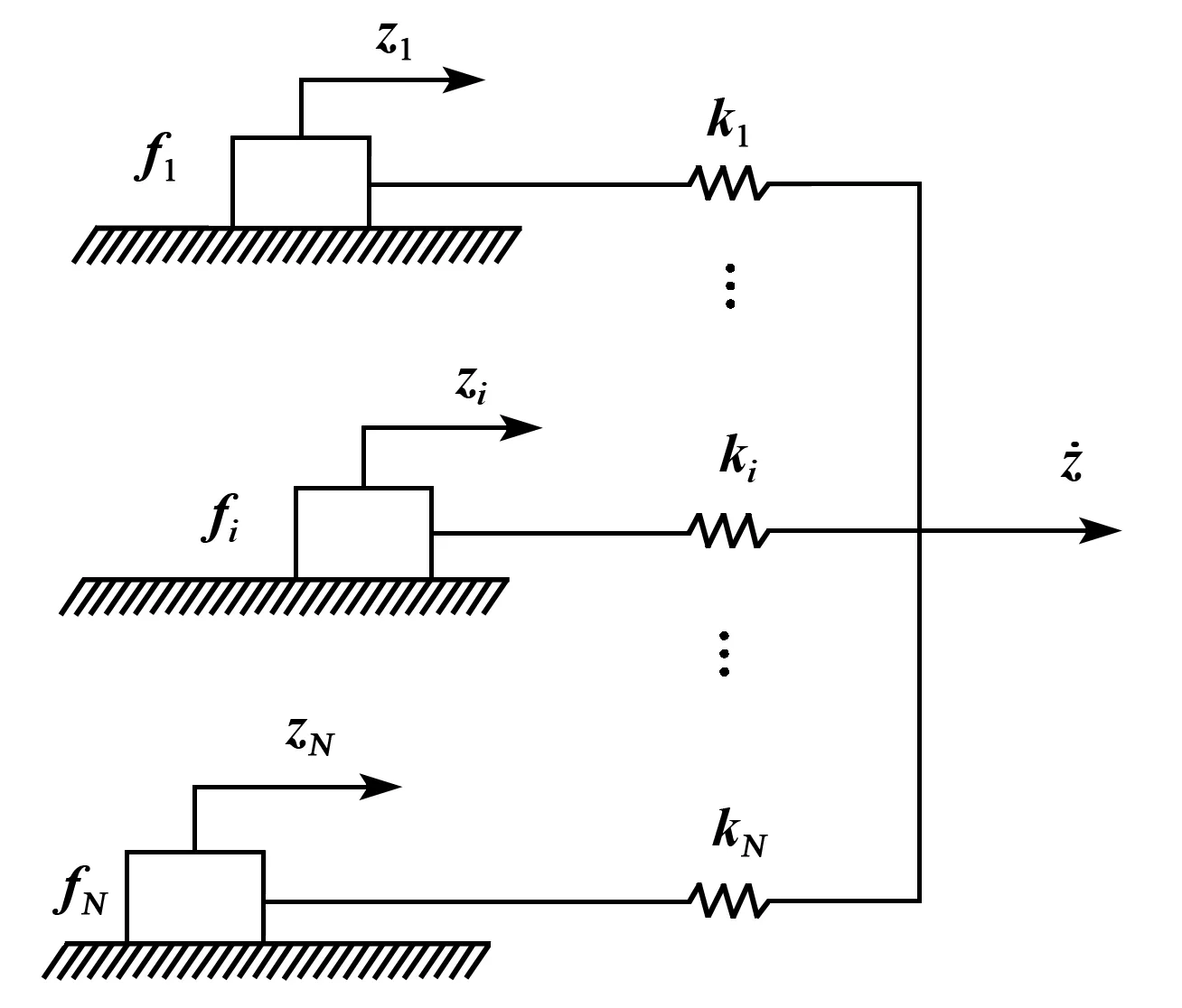
2 模型改进
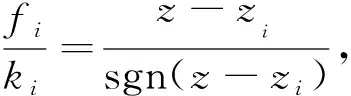

3 自适应控制算法


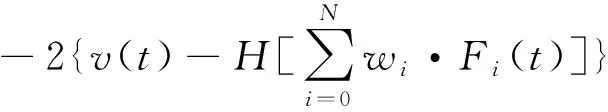
4 实验验证
4.1 实验方案

4.2 无前馈补偿的迟滞环

4.3 Maxwell-slip模型自适应控制的迟滞环

4.4 实验误差结果

5 结束语

