基于Baumolwaldf模型的家具物流中心选址应用研究*

□ 林鹏熠,姜晓红

(南京林业大学 汽车与交通工程学院，江苏 南京 210037)

家具行业近年来发展迅猛。2019年上半年，中国家具行业累计营业收入达3307.09亿元，具有相当规模以上家具企业6293家。与此同时，家具的出口量也大量增加。然而，我国家具物流在位于节点末端的城市家具配送环节中，存在分布不合理，很难形成高效有序网络的现象。因而家具物流配送中心的选址布局研究，对于家具物流和区域间经济发展具有促进作用[1-2]。

1 家具物流配送中心选址模型的确定

物流系统的合理化建设对于配送中心地域位置选择决策有着重要的作用。对于家具物流配送中心布局选址，单个仓储配送中心可能满足不了商品流通要求，因而确立多个仓储配送中心是很有必要的。供应商在其上下游的个体客户或某些家具专卖店形成一条密不可分的供应链，因此，相比起单一物流配送中心选址问题，多个物流配送中心选址问题更难，而鲍摩-瓦尔夫法是从物流成本出发，可以进行多目标、大批量运送的计算，且易于计算，能准确得出流通过程的总费用。因此，对于家具物流配送中心选址问题，采用鲍摩-瓦尔夫法进行选址分析更好[3-5]。

2 鲍摩-瓦尔夫模型的建立

假设有m个采购方向、n个区域物流服务对象和s个备选地址。满足假设：①货物在配送区域的集中或者疏散；②货源点的基点为所在区域行政中心；③供应点与路网之间考虑平路或山路。满足的约束条件有：①满足所有客户的需求；②考虑进货方向的供货能力；③货物在中转的进出流通量要相等[6]。

根据鲍摩-瓦尔夫模型建立目标函数为：

Xij>0Yij>0

其中，各参数分别为：K表示顾客，且k=1,2，…，n，Aj表示i进货方向的供应量，Bk表示k客户的需求量，Cij表示进货方向i到配送中心j的单位运输费用，Djk表示配送中心j到客户k的单位运输费用，Vj表示配送中心j的固定费用，Zj表示配送中心的货物流通量，Wj表示配送中心j每单位流通量的变动成本，Xij表示进货方向i到配送中心j的流通量，Yjk表示配送中心j到客户k的流通量。

鲍摩—瓦尔夫模型的目标函数要求配送中心选址规划方案的总成本最小，因为单位变动成本与流通量之间不符合线性关系，所以引进指数p，且0≤p≤1，以便符合规模经济的原则。此外，通过对节点数学模型的优化求解，选择一些备选地址，同时剔除一些备选地址。使已淘汰备选节点转移的货物量为零[7]：

详细计算步骤如下：

步骤1：求初始解

首先，计算从购买处到客户的所有运输费用，每两个点通过一个不同的配送中心，首先，令各候选配送中心的规模均为0，根据供应点经由配送中心再到需求点之间物资流通的所有组合求单位运输成本最小值，寻找运输成本最低的线路，其运输成本为：

引入变量表示从资源点i经由候选配送中心j再到需求点k的货物通过量，并使其受到以下约束条件约束，Uik分别等于商品的供应量与需求量：

步骤2：求二次解

设经由候选配送中心j的所有组合的集合为Zj，因此，各个候选配送中心j的货物通过量为:

以总运输成本和可变动成本之和达到最小化为目标。求得二次解为：

步骤3：求最优解

按照上面的步骤循环计算，得到结果Zj保持不变即可得到满意解。

3 实例分析与计算

以南京市某大型生产基地为例，南京某家具制造有限公司，它的生产基地占地约6万余平方米，大致分为3个生产基地，分8个客户方向，现模拟建立5个配送中心，得出合理的配送方案。已知家具配送中心的单位费用、进货方向以及家具配送中心向客户运输的费用、进货方向的供应量和客户的需求量分别如表1和表2所示，表中成本数据由各点间的相对距离确定，供应量和需求量根据各候选点员工人数和规模大小等因素决定[8-9]。

表1 家具进货方向到候选配送中心的单位运送成本

表2 候选配送中心到需求点的平均单位配送成本

已知候选配送中心存储变动费用函数如下表3所示，变动总费用由配送中心地理条件和规模大小决定。

表3 配送中心储存费用函数表

求初始解

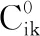
将下表4所示问题作为运输问题，将运输成本“按需就近”分派物资供应量并用表上作业法可求得到配送中心选址规划的初始解，如下表5所示。

表4 进货方向到客户方向所需的最小运输成本以及经由的候选配送中心

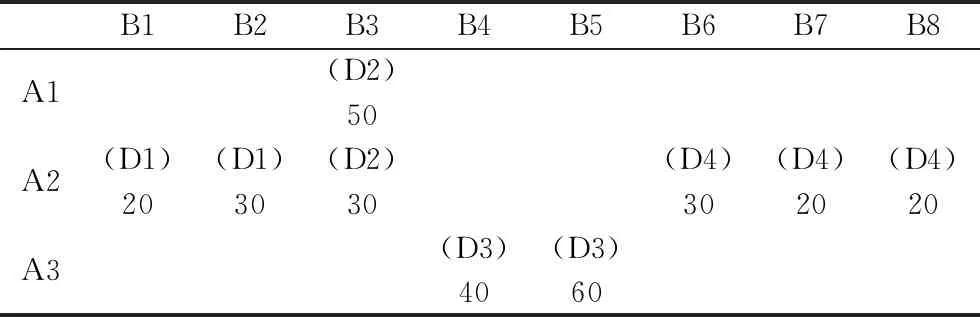
表5 配送中心选址规划初始解及经由的候选配送中心

求二次解

表6 根据初始解得出的各配送中心货物通过量和仓库变动费用率

表7 进货方向与客户方向最小运输成本及经由的候选配送中心

将上表7中数据仿照初始解，作为运输问题，计算二次解，然后计算二次解时变动费用率和货物通过量。继续迭代求多次解，计算得三次解时各配送中心候选点的货物通过量与二次解时一致，无需再进行求解计算，即得到最终解，如下表8所示。

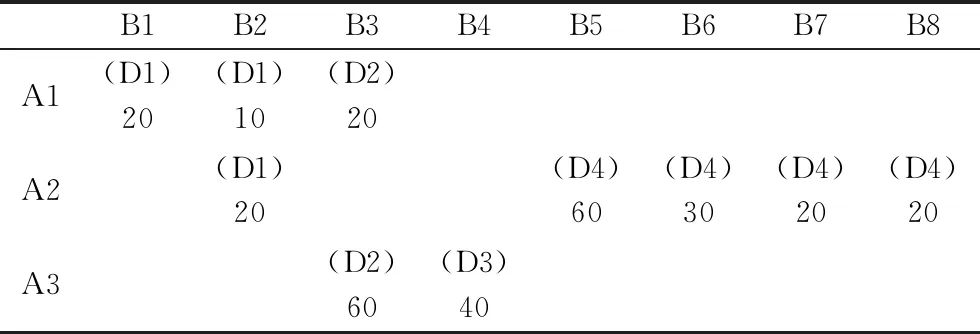
表8 配送中心选址规划最终解及经由的候选配送中心

最优方案是在候选的五个配送中心中建设D1、D2、D3、D4分配中心，其中D4仓库承担货物分配较多，应该着重建设，D3仓库起到分流的作用，承担货物分配较少。具体分配方案如下图1所示。

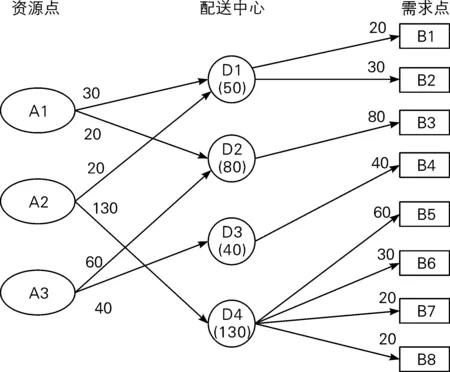
图1 选址规划分配方案示意图

4 结论与展望

本文结合相关配送中心理论，以南京市某家具企业为例，用鲍摩—瓦尔夫算法建立了一个配送中心选址的模型。通过采用迭代法进行计算，得到了运输成本最低的分配方案。由于此模型得出的结果与真实情况可能有出入，如最优位置建造地点上会有其他建筑及其他问题。因此，该方法仅为后续城市家具配送中心位置的选取提供一种参考。