10 kV线路老化与高阻接地故障对线损影响研究

丁丽丽

（新疆油田公司准东采油厂供电公司，新疆阜康 831511）

0 引言

随着中国经济与综合国力的逐渐增强，电力系统从普遍缺电逐渐变化到电力供给较为充足的局面，在这样的背景下，提高输配电系统的效率，减少各类损耗是节能减排的重要任务之一。配电网由于其线路长度长、结构复杂、分布面积广，并且各配网运行情况差异较大，其损耗占据了整个电力系统的主要部分，因此研究配网损耗来源以及提出各类降损措施十分重要。

国外对配电网线损方面的研究起步早，并且采用了多样的研究方法。文献[1]对电力网络中的有功和无功分配进行深入分析，总结提出了通过解决无功功率来降低线损的方法。文献[2]和文献[3]中提出运用潮流控制器对运行电网的电流和电压进行控制，使电力线路运行在最佳状态，从而降低线路电能损失。

由于传统理论线损计算原理简单、计算容易，在国内配电网线损方面得到了广泛的应用，传统线损计算方法主要有平均电流法、均方根电流法、最大负荷损耗小时法、损耗因数法等[4]，但考虑到的各类影响因素相对有限，并未对老化与高阻接地故障对配网线损的影响进行深入研究。一方面，从已有研究结果表明[5]，架空输电线路老化对线路阻抗有着较为明显的影响；另一方面，高阻接地故障不同于金属性接地故障[6]，其故障电流相对较小，不易被识别，其持续地对地放电会产生量级可观的损耗。因此，研究配电网的老化与高阻接地故障对网络损耗的研究十分重要。

本文基于此，首先通过拟合方法以实验数据为基础，建立了10 kV配电线路老化数学模型。然后通过实验统计数据建立了不同接地介质下的高阻接地附加损耗模型。最后采用等值电阻法，计算分析了算例配网中老化与接地故障分别对配电网线损的影响。

1 线路老化的数学模型

1.1 线路的等值模型

由于10 kV线路长度通常在100 km以内，其等值电路可以忽略分布参数对其的影响，即可用式（1）的集中参数来表示：

式中R表示总电阻；r表示单位长度电阻；X表示总电抗；x表示单位长度电抗；G表示电导；g表示单位长度电导；B表示电纳；b表示单位长度电纳。

图1 线路等值电路

通常10 kV线路不会发生电晕现象，其绝缘子泄露也很低，因而可认为G=0。此外电抗在电压等级不高时对电路计算的影响不大，也可认为X=0。因此，线路可以等值为如图1所示的Π形电路，其中Z=R+jX，故此线路被等值为总阻抗Z。

1.2 基于实测的线路老化模型

为分析线路电阻大小与老化和线路运行时间的关系，选取10kV配电线路常用的几种型号：LJ-150，LGJ-185，LGJJ-185，LGJQ-300作为实验对象，进行电阻测试。每个线路选取运行时间为2～22年的长度为10m的测试样本进行实测，为了更为直观的显著电阻的变化，将测试样本电阻折算到100 km长度，如表1所示。为更直观显示，将表1电阻变化数据绘制于图2中。

表1 折算100 km电阻值

图2 100 km线路老化过程电阻曲线

从图2中可以看出，4种线路运行4年以内的线路电阻率几乎没有变化，随后开始缓慢增加，并且10年后增速越来越快，到运行15年时，电阻率增加速度进一步加快。故线路电阻的变化基本符合指数增长规律，因此以式（2）所示的指数函数对电阻变化曲线进行拟合：

式中A，m，B为拟合参数。

利用MATLAB的拟合工具箱对4条电阻变化曲线进行拟合，拟合结果如式（3）所示，其拟合置信度均超过95%。

2 线路高阻接地故障的数学模型

在配网中，高达80%的故障类型是单相接地故障。高阻接地故障最明显的特征是故障电流很小，其值可能只有系统正常运行时负荷电流的10%，甚至更低[7]。国外研究实验数据表明，不同类型的高阻接地故障电流的典型值介于0～75A之间，具体数值如表2所示[7]。

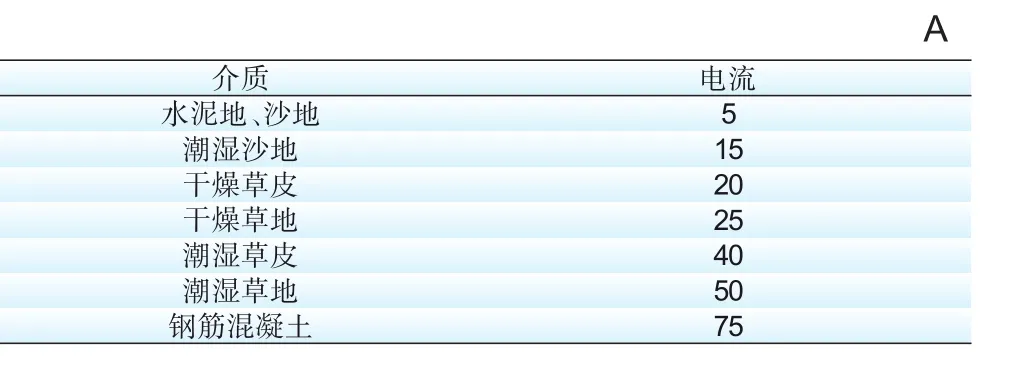
表2 高阻接地故障典型电流值

由于配电网高阻接地故障发生地点有很强的不确定性，并且其接地电阻阻值对于不同的接地介质变化也相对较大，因此建立一个确切的等值电阻模型有较大的困难。考虑到高阻接地故障的电阻值较大，其短路电流通常较为稳定，故可将故障点等效为一阻值恒定的电阻。其功率损耗可用式（4）表示，以作为线损的附加损耗。

式中PHIF为高阻接地损耗功率，IHIF为故障电流值，U为额定电压。

以额定电压10 kV计算，上述各类型高阻接地故障每处所产生的典型附加损耗如表3所示。

表3 各类型高阻接地故障典型损耗

3 配电网线损计算的等值电阻法

等值电阻法是一种近似计算线路可变损耗的方法，理论基础是平均电流法，它把配电网的可变损耗视为线路首端平均电流Iav通过线路和配电变压器的等值电阻Req所产生的损耗之和，即：

式中Ii和Ri分别为线路不同分段的电流和电阻；It和Rt分别为变压器电流和电阻。故配电线路等值电阻模型如图3所示。

图3 电阻等效模型

其中，线路导线等值电阻的计算依照绘制的单线图和各配电变压器二次侧总表抄见的电量，以线路电量递增的顺序即从线路末端到首端，从分支到骨干，按线段逐一进行计算。常用表达式为：

式中：Abi为线路上第i台10 kV/380 V变压器二次侧总表实际抄见电量；Abi·∑为第j段线路供电的变压器二次侧总表抄见电量之和；m为全线变压器的台数；n为线路分段的总段数；Rj为第j段线路导线的计算电阻。

同理，线路上所接变压器绕组总等值电阻计算的常用表达式为：

式中，RB·i是第i台变压器绕组归算到一次侧的等值电阻，由下式计算：

式中：ΔPk·i为第i台变压器的额定短路损耗功率；Se·i为第i台变压器的额定容量；U1N

4 老化与故障对线损影响算例分析

4.1 老化对线损的影响

以某地小型10 kV配电系统为例，其电网结构包含10台配电变压器，12段线路，所连变压器的总容量为490 kVA，线路平均功率因数为0.75。首先，将式（3）中100 km电阻拟合公式转化为电阻率变化公式，对应各段线路的长度，可以得到每条线路在不同年限的电阻。其次，通过等值电阻法计算得到不同年限的线路损耗与线损率，结果如表4、表5所示，并将表4和表5的数据绘制于图4、图5中。

表4 线路损耗

表5 线损率

图4 线损总量变化曲线图

图5 线损率变化曲线图

从以上计算结果可以看出，无论是配网线损总量还是线损率，都随着运行年限成指数增长。运行时间在10年以内的配网因老化带来的损耗较低，而当运行时间超过10年后，线损的增加较为明显，因此超过10年的线路是降损管理的重点。并且，负载率较低线路的线损率相较于负载率高的增长幅度要大，因此低负载的配网因老化而增加的线损更加显著。

4.2 高阻接地故障对线损的影响

由于高阻接地故障通常出现于规模较大的配网当中，以改进的IEEE-RBTSBus6测试系统中主馈线F4为算例[8]，如图6所示，包括1段母线26个馈线段，分布在乡镇、农村、山地三类区域，各区域所可能出现的故障介质如表6所示。该配网日平均负荷为4.815MW。

图6 高阻接地线损算例分析网络

表6 各类型高阻接地故障典型损耗

由于高阻接地故障发生的位置与接地介质具有不确定性，并且可能同时发生多处接地故障。为了模拟不同场景下高阻接地故障对线损的影响，本文采用配网可靠性评估中蒙特卡洛抽样故障元件的方式，随机生成几种场景。

步骤1：初始化仿真时间H＝0，故障时间TTF＝0。

步骤2：产生所有元件的正常工作持续时间TTF（TimetoFault）和故障修复时间TTR（TimetoRepair），依次排列形成每个元件在模拟总时间内的运行状态持续时间序列：

式中λi和μi分别为元件i的停运率和修复率；σ为（0，1）之间服从均匀分布的随机数。

步骤3：综合各元件的运行状态序列，确定TTF最小的一个或多个元件，认定为故障元件。

使用蒙特卡洛模拟抽样7次，抽样故障位置的同时抽样故障介质，根据表3数据计算每次抽样的接地损耗，并计算接地损耗率，结果如表7所示。

表7 各类型高阻接地故障典型损耗

从计算结果可以看出，当配网中出现多处高阻接地故障后会产生几百甚至上千千瓦的接地损耗，对于日均负荷为几个兆瓦的配网而言，其损耗率将会超过10%，考虑到线路自生的损耗，其总损耗将远远超出线损标准。而且，当配网出现高阻接地故障后，其不间断的对地放电会产生较大的功率损耗，并且产生的持续性发热将给线路周围安全带来很大的隐患。因此，无论从经济性还是安全性上，及时发现并处理高阻接地故障非常重要。

5 结语

本文一方面根据实测的配网线路老化数据建立了配电网线路的老化模型，另一方面以实验统计数据为基础建立了高阻接地故障的损耗模型，并通过算例分析了老化与高阻接地故障分别对配电网线损的影响，从而得出以下结论：

1）配电网线路的阻值随线路运行年限呈指数增长，导致线路损耗总量与线损率随运行年限也呈指数增长。

2）负载率较低的配网因老化带来的损耗增长要显著高于高负载线路，因此低负载线路也是配网减损的重点。

3）高阻接地故障带来的损耗是持续不断的，对于规模较小的配网而言，发生高阻接地故障后其线损率将大幅增加，以至于超过线损标准。