一种基于信息量的时空深度扫描模型

龙 华，王 美，杨 威，邵玉斌

(昆明理工大学 信息工程与自动化学院，昆明 650500)

E-mail：longhua@kmust.edu.cn

1 引 言

空间和时空扫描模型在预测预警模型中一直备受关注，自kulldorff[1，2]提出相应模型后，被广泛用于流行病[3-5]、生态学[6]，犯罪学[7，8]等诸多领域中.在时空扫描模型中，每个扫描窗口为一个集群对象，模型定义底面为扫描覆盖区域，高度为时间阈值的圆柱体为扫描窗口，根据窗口内外统计的发生与未发生事件得到似然函数，引入蒙特卡洛方法基于似然函数检测得到集群评估统计的显著性[9]，在最大扫描范围和最大扫描时间阈值内，不断迭代空间和时间得到各圆柱体窗口的显著性，从而获取到较高风险聚集区域.对时空扫描模型课题的研究中，决定扫描窗口的扫描半径、扫描时间阈值和扫描窗口形状，决定扫描统计量的测试统计量假设分布以及次级扫描区域即除了最大似然比对应区域以外的扫描区域处理等均是讨论的热点问题[10].

扫描窗口问题的讨论中，Patil和Taillie[11]创新性的采用上层设置的概念减小窗口大小使得能检测任意形状的簇，提升集群检测能力，Duczmal和Assunção[12]则采用模拟退火方法，基于图的算法连通子图空间找到似然比局部最大的区域，Kulldorff[13]和Christiansen[14]讨论了使用椭圆形窗口替代经典模型中圆形扫描窗口，并证明在特定数据集中有一定的优势；测试统计量假设分布的讨论中，较有代表性的是2014年Cançado[15]提出了零膨胀扫描统计量(zero-inflated Poisson ZIP)，在该模型中当数据集包含大量零时，为了提高扫描结果中的空间精确度和空间召回率，将零分为符合泊松分布的抽样零和独立随机变量得到的结构零，对该模型的有效性检验可查阅Allévius 和Höhle[16]于2019做的模拟研究实验，此外还有测试统计量符合超几何分布的情况等.在前述方法模型中均会涉及一个问题，即扫描过程会产生成千上万相互重叠的重要集群，这类集群会模糊较风险区域的判断，传统时空扫描以及前面提到的改进模型均按Satscan层次结构将其直接删除，只报告不相交不重复的集群，但很明显该方法会损失很多对信息量更有贡献的集群[17].

为了充分利用潜在集群的信息，Gangnon[18]使用加权平均似然比检验统计量，将重叠集群用似然比加权合并，该方法只适合集群相对较少的情况，集群较多时会合并成较大而无实际报告意义的集群，李小洲和王劲峰[19]用优化选择格网点间隔方法和多重排序算法，以达到减少候选聚集区域的遗漏，并在较短的时间内删除所有的重复候选聚集的目的，该方法删除的是完全重复的集群，仍然留下大量交集较大的集群模糊较风险区域的判断，同样不能达到很好处理次级区域的效果，Gangnon与李小洲各自所提方法总的来说都存在不能量化分析实际效果的问题，直到2016年Han和Junhee[17]提出使用基尼系数--一种量化分析次级区域的方法来确定最优的集群，如当一个大的集群里面包含几个小的集群时，比较大的集群根据观察数据和预期数据得到的基尼系数与其包含的小集群同样方法计算得到的基尼系数，选择报告基尼系数较大的区域，减小信息量的损失，从所举例子可知其使用对象导致Han和Junhee所提方法有一定的局限性，Han和Junhee所提方法是在保持传统方法使用层次结构删除扫描重复窗口的情况下，再次使用基尼系数做判断，所以分析的过程中会存在很多问题，如文献[19]说的他们只考虑了紧凑的簇所以显示结果良好，但实际使用中并不理想，如文献[20]提出的基于基尼系数分析时在即使单个较大的群集确实有一定意义的情况下，往往会导致报告的是多个较小的群集.

为了充分利用潜在集群的信息，同时不出现Han和Junhee误报告的问题，我们提出一种基于信息量的时空深度扫描模型IN-scan model，引入信息量I(p,G)，p为统计值，G为基尼系数，从信息量的角度出发量化每一个扫描集群，在不做删除重复扫描区域，充分利用有效信息的情况下，报告出较有意义的集群.

2 时空扫描模型相关概念

2.1 置信度

时空扫描模型，主要是找出聚集性较高，即置信度(1-p)较大的集群，模型中似然函数值反应一个窗口为聚集域的可能性，即最可能的聚集域是最大化对数似然比对应的扫描窗口，此时测试统计量T=maxZLog(LR(z)).假设我们研究区域是Z，z表示某个扫描窗口，其似然比表示如下：

(1)

其中，cz和μz分别表示扫描窗口z内的观察案例和预期案例，C=∑z∈Zcz和N=∑z∈Zμz分别表示扫描区域Z内的总观察案例和总预期案例，在模型中如果只对较高可能为聚集域的扫描分析感兴趣则使用如公式1中的指示函数I(cz>μz)，若考虑的是较不可能为聚集域的使用I(cz<μz)，若二者均考虑则删除指示函数，在本文的研究中仅考虑第一种情况.

得到各扫描域的似然比值，还需要对其进一步分析属于非随机的置信度(1-p)，求解p值目前有两个方法一个是测试统计量T看做近似服从于极值分布[21]做计算，一个是采用蒙特卡罗(Monte Carlo)假设检验方法求解，因为T真实服从的分布还有待研究，故文中选后者方法.使用Monte Carlo计算得到p=rank(LLR)/(M+1)，LLR为真实数据集扫描域计算得到的似然比，M个随机数据集是根据真实数据集采用重排算法得到的，M个随机数据集对应计算得到M个LLR′，将真实的LLR与M个LLR′放在一起由大到小排序返回排序值rank(LLR)，由此计算得到p值.p值越小对应聚集域属于非随机的置信度越大.后面提到的pi表示第i个扫描窗口对应的统计值.

2.2 LR-scan 模型

LR-scan模型是使用了对数似然比为测试统计量并引入了Junhee提出的基尼系数判别方法的最新时空扫描模型，该模型首先是根据置信度得到最大的聚集域对重复域进行一次删除，然后根据基尼系数对重复域进行再一次筛选.该方法依然存在信息浪费与报导有偏差问题，故本文提出IN-scan模型.

LR-scan模型已于SaTScan中更新，SaTScan是用于时空扫描统计分析的一个开源软件，其集成了很多时空扫描的方法.当前，LR-scan 模型是最新添加的方法，因此文中也将LR-scan方法称为最新SaTScan方法.

3 基于信息量的时空深度扫描模型

时空扫描方法属于预警模型，集群置信度越大越容易报警，即其区域内发生事件的概率越大.在IN-scan 模型中，我们将每个集群的置信度视为集群内事件发生的概率，进而计算事件均值和基尼系数，然后根据求得的p和G计算信息量.图1是我们提出模型的结构，首先与LR-scan 模型一致以对数似然比为测试统计量进行扫描计算，但IN-scan不对扫描结果进行删除，而是对其求均值，以进行二次以信息量为测试统计量的扫描计算，然后依次报导较风险的聚集域.本节将给出各个参数的计算方法.

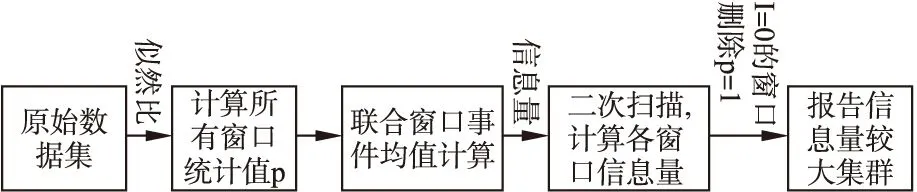
图1 基于信息量的时空深度扫描模型结构Fig.1 IN-scan model structure

模型特点为：

1)只考虑较高可能发生性事件，故始终有地点i观察案件数oi大于等于预测案件数μi；

2)使用均值数据，n′i和μ′i；

3)于L中二次扫描，测试统计量使用信息量I(p,G).

3.1 事件均值计算

假设图2中3个集群的扫描条件均一样，且扫描时间也一致，此时结合表1记录以地点A为例有：nA1=nA2=nA3=nA，μA1=μA2=μA3=μA,加入事件发生的概率，计算地点A数据的均值：

(2)

地点B和C与A分析一致.这样计算完成后相当于把cluster1、cluster2、cluster3的信息映射到扫描区域L中，二次扫描时只用分析L中的数据即可，见方法介绍模块.

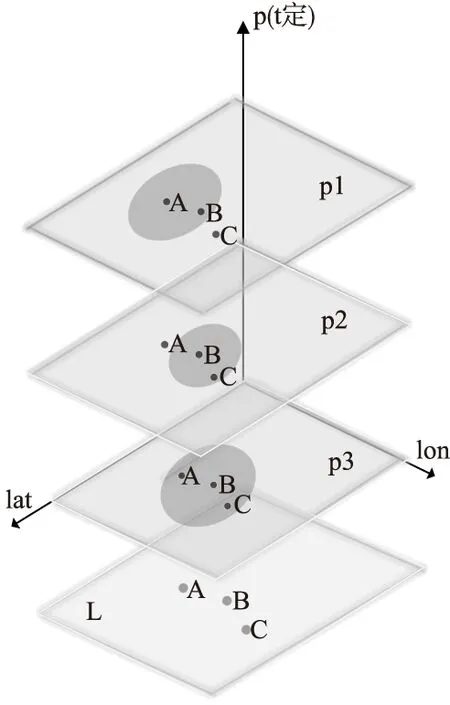
图2 均值分析-聚集域分布图Fig.2 Mean analysis-aggregation area distribution map

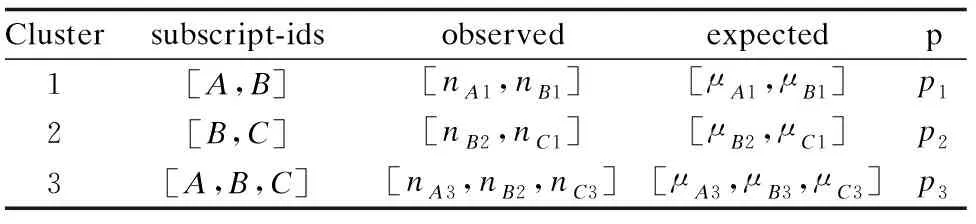
表1 均值分析-聚集域记录Table 1 Mean analysis-aggregation area recording

3.2 基于事件均值计算的基尼系数

基尼系数[22]是洛伦兹曲线的一个度量值，洛伦兹曲线[23]主要用于经济领域，如图3所示基尼系数G=S1/(S1+S2),G越大说明收入分配越不平等.Han和Junhee首次将G用于时空扫描模型中，其横纵轴分别表示观察到案例的累加

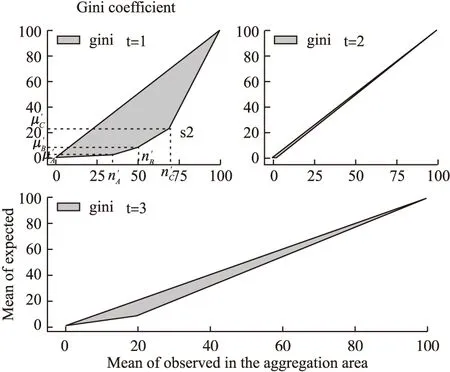
图3 聚集域基尼系数显示图Fig.3 Aggregation area of Gini coefficient

百分比和预期案例的累积百分比，G=0时，即说明该集群无显著性，而G越大，对应扫描域的置信度(1-p)越大，Han使用G是为了报告出更有意义的集群，在我们的研究模型中，研究G亦是为了报告出能提供更多信息量I的集群.

在对IN-scan model模型的研分析中，由于我们使用的是均值数据，地点i观察案件数n′i与预测案件数μ′i能综合反映i点的风险度，此时地点i与地点j信息相对独立，所以在扫描区域L中进行二次扫描时，测试统计值信息量I(p,G)中的G我们使用扫描域内的n′从小到大排序后计算得到，见图3，假设扫描域为table1中的cluster3，扫描时间为1天，此时若n′c>n′B>n′A，见图4中t=1的G显示图，图中阴影部分占下三角的面积百分比即为G值，t=2和t=3类似分析，从图3中可看出就基尼系数来说，cluster3扫描时间为1天时G较大.在IN-scan model中，结合p与G值计算各条件下的集群的信息量，报告I最大的集群.

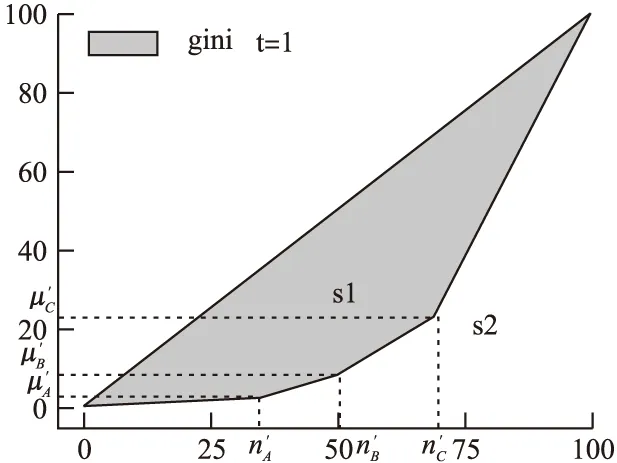
图4 t=1的G显示图Fig.4 G display of t=1

在考虑全部潜在集群的分析中，计算基尼系数时，使用事件均值计算可减小误差，如图5是基于Satscan样本数据集纽约市医院记录的发烧案例，在Satscan和我们最终模拟实验中知道图中两个扫描区域是以171为中心的窗口较异常优先报告，当直接使用观测值计算基尼系数时，见表2，169对应的基尼系数明显高于171对应的值，在传统模型中由于使用层次结构的方法提前删除了169对应窗口，所以不会报告，说明在不做删除重复扫描区域的情况下，直接使用观测结果和基尼系数做判断会产生误差，基于此问题，我们充分利用有效信息，对各扫描点做均值后再次扫描计算基尼系数，比较出基尼系数较大的窗口，表3是使用提出方法实验的结果，可看出能正确比较出171对应窗口.考虑到基尼系数和显著性统计值，均能反应信息量的大小且相互影响，所以我们将引入信息量I(p,G)分析最终结果.

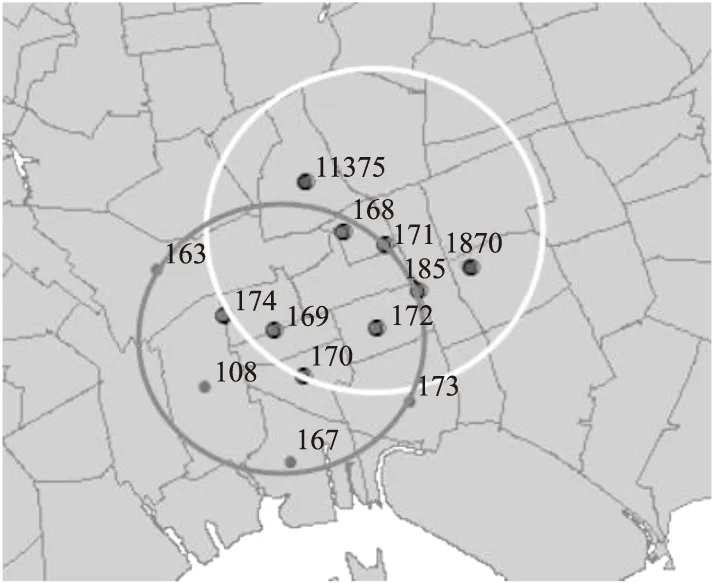
图5 相交窗口分析Fig.5 Intersection of windows with center 169 and 171

3.3 基于p和G的信息量计算

在很多领域信息量都是作为选优条件的评估指标，如地质学[24]和工程学[25]，尤其在预警领域，很多时候会由于信息量较少导致大量的假预警报告，所以更应该考虑信息量因素，信息量表达式为I(x)=-log2p(x)，其中p(x)表示事件x发生的概率，p(x)越小信息量I越大.对于我们模型来说I∝(1/p)，I∝G，所以有：

表2 Han和Junhee方法重叠圆分析结果Table 2 Analysis result of the intersecting windows by Han and Junhee

表3 使用均值方法重叠圆分析结果Table 3 Analysis result of the intersecting windows with mean value

备注：表中center:扫描中心点，r (Km):扫描半径(单位是千米)，ids:扫描窗口包含的地点集合，observed:扫描窗口内总的观察案例数，expected:扫描窗口内总的期望案例数，p：显著性统计值，G：基尼系数.

I(p,G)=-logp-log(1-G)p∈(0,1],G∈[0,1)

(3)

显著性统计值p越小，基尼系数G越大，信息量I越大.集群I越大,越优先报警.

4 评估方法

为了评估基于信息量的时空深度扫描模型的空间精度，结合机器学习中的评估方法[26]以及2012年Neil[27]提出的空间精确度SP和空间召回率SR，文中使用F-Score作为模型评估指标.此处若Z*表示检测到的聚集空间区域，ZT表示真实爆发区域，则有：

(4)

|Z*|和|ZT|分别是Z*和ZT包含的地点数，若向集群中多添加地点将有利于召回率同时精确率会有所下降，若从检测的区域移除地点会造成以召回率为代价提高精确率结果，故需要同时权衡SP和SR.在模型中我们不希望|Z*|很大，导致SP很小，但SR很大的情况，SP和SR同样重要，故评估参数F-Score表达式如下：

(5)

5 实验与分析

时空扫描统计方法应用于多领域，2008年Vadrevu[28]和Tuia应用时空扫描方法监测火灾风险区域取得一定成效，本次实验中我们将采用旧金山的火灾数据展开讨论.实验数据集来自旧金山地区数据协调网站DataSF1提供的“Fire Department Service”火灾记录公开数据集，数据集中包含旧金山18年和19年上半年共四万余条火灾记录数据，且网站在实时更新中，考虑实验的回顾性验证所以实验数据集随机提取2018年1月和3月的火灾事件进行研究.图6是数据集中旧金山火灾发生的地点标记图.

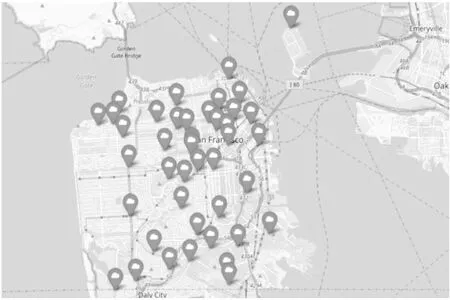
图6 旧金山火灾观测地点图Fig.6 San Francisco fire observed sites

5.1 结果与讨论

本节中用IN-scan表示我们提出的基于信息量的时空深度扫描模型，LR-scan表示现有最新时空扫描模型，实验中使用IN-scan与LR-scan的扫描结果比较，说明新模型的有效性.首先选取时间2018年1月8号-14号的数据进行分析，扫描半径设置为r=5Km，最大扫描时间t=3day，首先基于似然比测试统计量不删除重复窗口进行扫描，并使用蒙特卡罗计算扫描得到的每个扫描窗口的置信度，表4中输出前5个扫描结果.最大扫描时间为3天，故实验结果中包括扫描时间分别为1天、2天和3天的情况，实验中会分开计算，这里以分析t=1为例，如表4中第一个模块中最大似然比对应包含扫描区域为12，获取以12为圆心的所有同心圆包含的地点集合D12，之后获取以D12包含的地点为扫描中心的所有窗口，然后按照事件均值求解方法算出各地点的均值，计算结果见表5，表中obaerves和expected是地点的观测值和预期值，obaerves-mean和expected-mean是地点的观测值均值和预期值均值，表中有观测值不一定有观测期望值，如locations 2 观测值为2，但观测期望值为0，是因为包含有地点2的全部窗口置信度都为0导致，也有观测值很小，但观测期望值很大，如locations 12，因为地点12自身的观测值很大，包含有地点12的窗口置信度多数偏高，故观测期望值很大.基于期望值求取各窗口的基尼系数，使用基尼系数和置信度随之求取各窗口的信息量，表6即为表4中第一个扫描窗口计算得到的信息量I，在计算结果中留下最大信息量对应窗口，同时取剩下的第一个集群重复分析取出信息量最大的窗口，如此循环直到I=0停止.

表4 1.8-1.14，r=5Km前五个扫描结果Table 4 Top five scan results from 1.8-1.14，r=5K

表5 1.8-1.14 t=1 均值表Table 5 Mean values from 1.8-1.14，t=1

表6 地点12，t=1信息量计算Table 6 Information calculation of location 12，t=1

实验选取2018年1月8号-14号与2018年3月8号-14号做扫描对比实验，首先确定真实爆发区域ZT.实验最终比较的是模型对异常地点检测的准确性和回归率，因为我们考虑的是短期爆发事件，故文中爆发定义为扫描时间后对应的第一周内发生事件，见图7可得1.15-1.21爆发地点集[1，2，3，7，8，10，11，12，13，14，16，20，23，24，25，26，27，29，32，34]，3.15-3.21爆发地点集为[1，2，3，5，6，7，10，12，13，15，17，20，21，25，33，39].对比结果见表7-表9.

表7 1.8-1.14，r=5 km扫描结果比较Table 7 F-Score comparison from 1.8-1.14，r=5 km

表8 3.8-3.14，r=5 km扫描结果比较Table 8 F-Score comparison from 3.8-3.14，r=5 km

表9 3.8-3.14，r=3 km扫描结果比较Table 9 F-Score comparison from 3.8-3.14，r=3 km

表7扫描时间1月8号-14号，扫描半径为5km，运用评估模块的计算方法，得到相比LR-scan，IN-scan的F-Score提高14%；为了验证方法的有效性使用时间段3月8号-14号，扫描半径为5km进行扫描，见表8相比LR-scan，IN-scan的F-Score提高18%；实验3选取同一时间段3月8号-14号，但不同扫描半径(3km)进行扫描，见表9相比LR-scan，IN-scan的F-Score提高12.6%.总体比较，IN-scan模型较现时空扫描模型F-Score性能评估值提升10%以上.

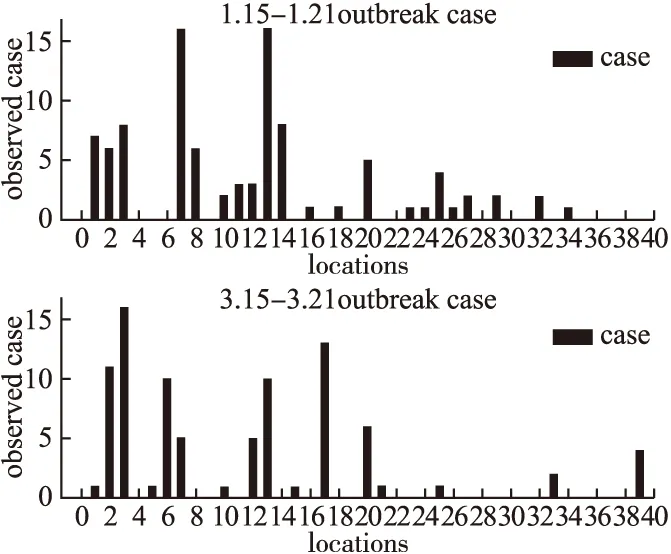
图7 1.15-21与3.15-21火灾爆发统计图Fig.7 Fire outbreak statistics comparisonbetween 1.15-21 and 3.15-21

5.2 结果分析

从实验结果来看，现存在的时空扫描方法中对扫描过程产生的大量重复域直接进行删除确实存在一定的缺陷，或是留下了置信度大但信息量很小的聚集域，或是剔除了置信度小但信息量大的聚集域，即使向LR-scan模型加入了基尼系数进行第二次判断也不能避免此类问题，一定程度上会加重该问题，因为LR-scan模型中进行基尼系数计算时，往往会报告多个较小的群集，而该类集群往往是置信度大但信息量较小.可见我们提出的IN-scan模型在综合处理权衡聚集域的置信度与信息量上有一定优势.

6 总结与展望

在时空扫描方法中，每次扫描都会产生成千上万大量有重复的集群，现有研究方法会按Satscan层次结构删除此类集群，或者用似然比加权集群分析.每个集群都会对应一个置信度，都能得到直观反应他们异常度的基尼系数值，故不应该直接删除或合并，所以为了充分利用扫描域提供的信息，量化分析选取报警区域，我们提出了一种基于信息量的时空深度扫描模型，深度是因为进行了二次扫描，基于信息量是因为我们利用每个聚集域的观测值均值和预期值均值计算得到基尼系数G和基于似然比扫描的得到的统计值p得到信息量IN展开比较报告较有意义的集群，经过实验对比，确实有一定有效性.

另外本文介绍的IN-scan模型具有很强的稳定性.现有模型中当存在多个集群时需要使用适用于多个集群的估计方法进行进一步分析，而IN-scan模型可以对重复的多个群集进行分析，直接计算相交群集中的事件所包含案例.就目前的研究来说，我们仅考虑单个事件类型，而忽略了事件间的内部结构差异造成的影响等，即考虑多元变量问题，这是我们下一个主要研究的方向.