一种面向混合型数据聚类的k-prototypes聚类算法
贾子琪,宋 玲
1(广西大学 计算机与电子信息学院,南宁 530004)2(广西多媒体通信与网络技术重点实验室,南宁 530004)
E-mail:jqian@gxu.edu.cn
1 引 言
聚类旨在找出数据集内子簇之间的相关性,并评估这些子簇内数据对象之间的相似性[1].假设数据集中的每个数据对象都由m个特征描述,聚类算法的目的可以表述为“将数据集D划分为k(k∈N+)个不同的子簇,使得每个子簇内的成员彼此之间尽可能相似,不同的子簇之间的成员彼此之间尽可能相异”.
在数值型数据聚类领域中,经典的k-means算法[2]以每个特征值的平均值表示簇中心.只能处理数值型数据.k-means算法依据待聚类数据对象和簇之间的距离进行聚类划分.在分类型数据聚类领域中,经典的k-modes算法[3]用mode向量表示簇中心,mode向量是子簇中每个特征中出现频率最大的特征值组合而来的.k-modes算法通过简单汉明距离计算待聚类数据对象和簇之间的相似性,以进行聚类划分.但是,简单汉明距离不能有效的计算高维数据的相异度.不管是k-means算法还是k-modes算法都只能处理单一类型的数据.在一些实际应用中,人们不仅要处理数值型数据还必须处理诸如性别、颜色和疾病类型等的分类型数据.换句话说,包含数值型和分类型的混合型数据集在实际任务中无处不在.但是,在聚类分析中处理混合类型数据是很复杂的,因为数值型数据和和分类型数据之间存在很大的差异.为此,论文提出了一种混合型相异度系数,以计算待聚类数据对象和簇之间的相异度.随后,论文基于混合型相异度系数提出了一种混合型数据聚类算法“一种面向混合型数据聚类的k-prototypes聚类算法(KPMD)”,为每个待聚类数据对象划分合适的簇.使用KPMD算法的优点是不需要人为的设置各种参数,并且对待聚类数据的类型没有限制,可以同时处理数值型数据、分类型数据和混合型数据.
论文的其余部分安排如下:第2节,相关工作叙述;第3节,问题陈述、相关符号描述和经典k-prototypes算法描述;第4节,论文提出的算法(KPMD);第5节,实验及结果分析;最后,第6节,论文得出的结论.
2 相关工作
本节阐述当前一些与基于相异度系数的混合型数据聚类最相关的重要聚类算法.
在实际的聚类划分中,需要处理大量的高维数据集以及由分类型数据和数值型数据组成的混合型数据集.处理混合类型数据的一种简单方法是预处理,直接将分类型特征转换为数值型特征.例如将分类型特征转换为二进制字符串,然后用基于数值型数据的聚类算法进行进一步的聚类划分.然而,用二进制编码进行预处理有四个缺点:第一,破坏了分类型数据的原始结构,导致转换后的二进制特征没有意义;第二,忽略了隐含的相异度信息,不能真实地反映数据集的结构;第三,如果特征值的值域很大,那么转换后的二进制特征值将具有更大的维数;最后一个缺点是维护困难,如果为分类型特征添加新的特征值,那么所有的数据对象都将发生更改[4].为了更好地解决这些问题,许多研究人员对基于相异度系数的聚类算法进行了研究,寻找能直接处理混合型数据的有效方法.k-prototypes算法[5]及其变形算法是基于同时考虑数值型特征和分类型特征的相异度系数的混合型数据聚类算法,此类算法可以同时处理分类型和数值型数据,但是需要人为设置聚类参数.Li[6]提出了一种基于相异度系数的聚焦聚类(SBAC)算法,该算法基于Goodall相异度[7].在不预先知道特征值基本分布的情况下,对相异度系数中出现的不寻常特征值赋予较大的权重.该方法对混合型特征的处理能力较好,并且可以避免分类型数据和数值型数据之间的参数调整,但是该算法具有很高的时间复杂度.COOLCAT算法[8]是一种基于熵的分类型数据聚类算法,使用熵初始化簇中心,旨在最小化期望熵,但在处理分类型数据时不能体现特征之间的簇内相异度.OCIL算法[9]是基于无参数的混合型聚类算法,基于熵给出了统一的相异度系数.和k-prototypes及其变体一样,OCIL算法使用k-means范例来处理混合类型数据,是一种迭代聚类算法,对初始化敏感,更适合于球形分布数据.Sangam[10]提出了一种基于相异度系数的EKACMD算法.EKACMD算法是k-prototypes的变体算法,通过对相异度系数进行改进来提高混合型数据聚类的准确率.EKACMD算法在一些情况下能较充分的考虑数据的结构特点,但在分类型数据各特征值出现频率相等的情况下不再适用.
针对上述问题,首先,论文基于簇内簇间相异度、信息熵和最大最小值标准化提出了新的混合型相异度系数.该混合型相异度系数具有统一的标准,能够自动设置分类型和数值型数据之间的权重参数,消除了分类型数据和数值型数据之间的计算差距,避免了分类型和数值型数据之间的特征变换和参数调整.接着,提出了一种面向混合型数据聚类的k-prototypes聚类算法(KPMD),KPMD算法可以进行无参数聚类分析,适用于分类型,数值型和混合行数据聚类.实验结果表明,与经典的k-prototypes算法等算法相比,KPMD可以获得更好的聚类结果,且不需要人为手动的设置各种参数.
3 经典prototypes聚类算法及问题描述
3.1 相关符号说明
为了便于表示和更好地理解问题,论文使用的一些相关符号及其含义说明如表1所示.
3.2 k-prototypes聚类算法
Huang[5]将k-means算法和k-modes算法结合起来,提出了针对混合型数据聚类的k-prototypes算法.具体方法是,将数值型部分的“means”和分类型部分“modes”组合起来,构建了一个新的混合型簇中心“prototype”,并以prototype为基础构建了一个适用于混合型数据的相异度系数公式和目标函数;引入权重γ来控制数值型特征和分类型特征对聚类过程的影响;采用k-means算法的基本思想,直接对混合型数据进行聚类.
假设使用k-prototypes算法对数据集D={xi,1≤i≤n}进行聚类.根据每个数据对象的m维特征的相异度,将数据集D划分为k个子簇,对应k个prototypes.1≤s≤p为分类型数据的维度数,p+1≤s≤m为数值型数据的维度数.k-prototypes算法是将混合型数据的相异度系数分成两个部分单独计算的,其中数值型部分采用欧氏距离的平方,分类型部分采用简单汉明距离[11].两种类型数据之间的权重采用权重系数γ来进行调节[12],如公式(1)所示.
(1)
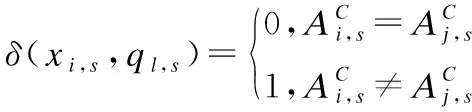
γ是用来调节两种类型数据在相异度系数中的比重,避免聚类结果值偏向分类型特征或者数值型特征,是k-prototypes算法的一个重要的可调节参数.k-prototypes算法的基本步骤描述如下
算法 1.k-prototypes聚类算法
输入:聚类个数k;包含n个对象的混合型数据集D;
输出:完成聚类的k个簇C={C1,…,Cl,…,Ck};
Step 1.在数据集D中随机选取k个数据对象作为初始簇中心;
Step 2.根据公式(1)计算数据集中的所有数据对象xi与簇中心ql之间的距离,根据最近原则将这些数据对象分配到离它最近的簇中去;
Step 3.更新簇中心.重新计算每个对象与当前簇中心之间的相异度;分类部分采用出现频率最高的值,数值部分采用求平均值的方法来确定;将xi重新分配到距离它最近的簇中去;
Step 4.确定每个簇中的簇中心不再发生变化,即目标函数的值不再发生变化;如果达到,则算法结束;否则跳至Step 2继续执行,直到目标函数值不再发生变化为止;

表1 符号说明Table 1 Symbolic description
3.3 问题描述
k-prototypes算法由于其原理简单,易复现已经在混合型数据聚类中得到了广泛的应用.但是,其相异度系数中的参数γ需要人为确定,对聚类结果影响很大;对分类型和数值型特征的相异度计算也存在缺陷,没有充分的考虑两种类型数据的结构特点和数据集整体的分布.
借助表2所示的人工数据集D1来讨论用户指定权重γ在聚类过程中的缺点.人工数据集D1包含27个数据对象,每个数据象由两个数值型特征和一个分类型特征描述.分类型特征A3具有三个特征值DOM(A3)={A,B,C}.数值型特征A1和A2的取值均在0-80的范围内.
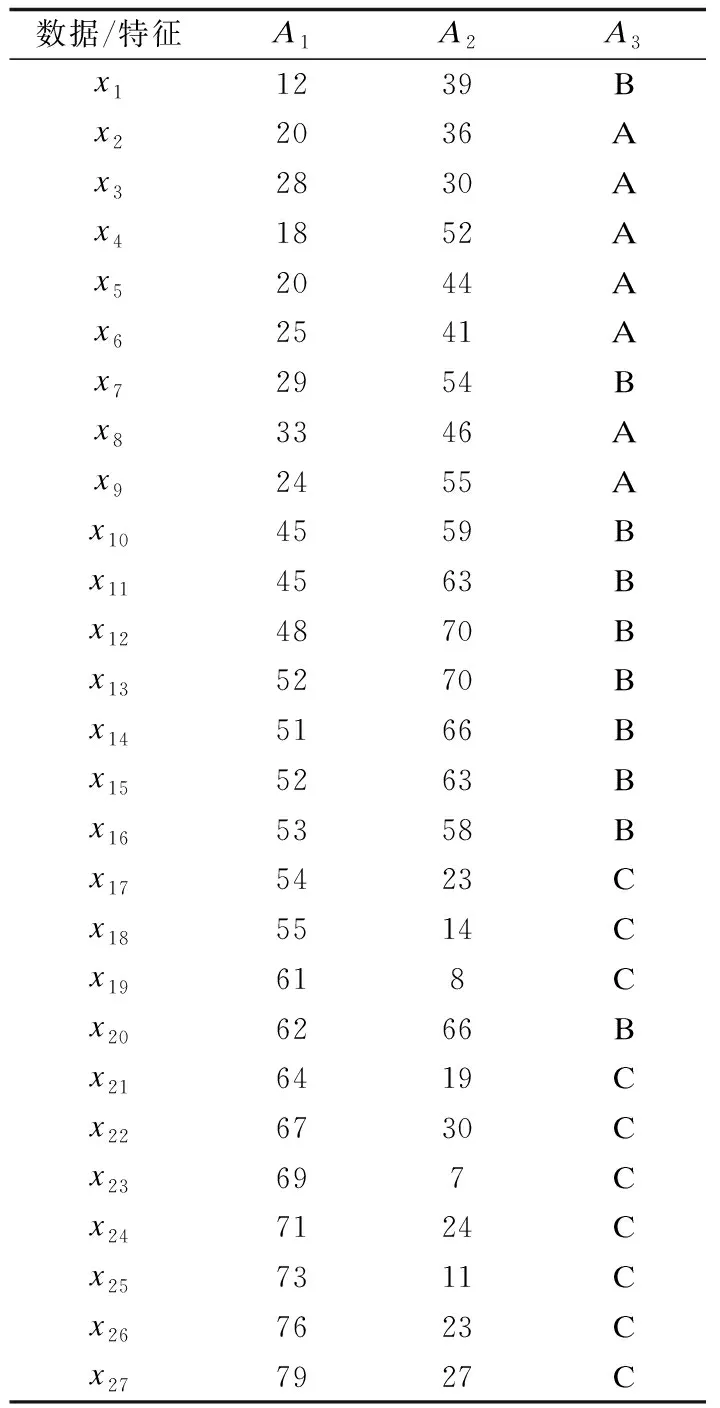
表2 人工数据集D1Table 2 Artificial data set D1
关于特征A3,规定特征值为A,B,C的数据对象分别用实心三角形、实心圆、实心正方形表示.当权重γ=0时,人工数据集D4的聚类结果只取决于A1,A2两个特征.其聚类结果如图1所示,该数据集有三个簇.为了方便观察,用虚线将三个簇分隔开.当γ>0,则数据对象x7可以移动到C2,因为对象x7和簇C2中大多数数据对象的特征A3是相同的.类似地,基于上述原因,数据对象x10可以移动到簇C1.权重γ的不确定,导致数据对象x7和x10是偏向数值型部分还是分类型部分也是不确定的.数据对象x1和x20可能仍然保留在原来的簇中,因为它们距离临近的其它簇太远了,即使它们与临近的其它簇中的数据对象有相同的特征值.综上所述,在相同尺度上定义数据特征和分类型特征的权重是很重要的.
4 一种面向混合型数据聚类的k-prototypes聚类算法(KPMD)
论文提出算法的动机主要有两个方面:是为了给混合型数据聚类提供有效的相异度系数表示方法;另一方面是考虑不同特征对聚类的重要性.基于上述动机,首先,本节基于熵理论提出了基于熵权的分类型相异度系数;然后,基于最大-最小值标准化理论提出了量化的数值型相异度系数;此外,经过综合讨论提出了适用于混合型数据聚类的混合型相异度系数;最后,将提出的混合型相异度系数应用到经典k-prototypes算法上,提出了一种面向混合型数据聚类的k-prototypes聚类算法(KPMD).

图1 人工数据集Di的聚类结果Fig.1 Clustering results of artificial data set Di
4.1 基于熵权的分类型相异度系数
为解决对信息的量化计算问题,1948年Shannon引用热力学中热熵的概念提出了“信息熵”的概念[13,14].信息熵可以用于计算数据的离散程度,可以为各维特征分配合适的权重提高聚类效果.熵与聚类的关系可以理解为,由相似数据对象组成的簇比由不相似数据对象组成的簇的总熵值要小.相反,如果相似的数据对象被分在不同的簇中,它们的熵值会更大.数据集越复杂,不同特征数据越多,数据集的信息熵就越大.将信息熵的概念引入到权重的计算中,可以定量的计算特征值构成的差异程度.Shannon的信息熵公式[15]定义如公式(2)所示.
(2)

性质 1.非负性.En(x)=-∑x∈Dp(xi)log(p(xi))≥0,公式(2)包含负号,这是为了确保信息量的值恒大于等于0.
性质 2.对称性.函数的所有变量可以互换,而不影响函数值.En(X)=En(p(x1),p(x2),p(x3),…,p(xn))=En(p(x2),p(x1),p(x3),…,p(xn))=En(p(x3),p(x1),p(x2),…,p(xn)),其中i=1,2,…,s.
在聚类过程中,某分类型特征的重要程度与该它的差异程度成反比[15].在一定程度上,每维分类型特征的信息熵反映了每维分类型特征的权重ws.因此,论文根据各维分类型特征取值的不确定性,利用信息熵来计算各维分类型特征在聚类过程中的重要程度,为相异度系数分配权重.
定义 1.特征值的簇内相对频率

(3)
定义 2.特征值的簇间分布频率
(4)
定义 3.分类型相异度系数
令dC(xi,ql)表示混合型数据集分类型数据部分的相异度,满足公式(5).
(5)
其中,δ(xi,s,ql,s)定义如公式(6)所示.此定义的前提是,每维分类型特征占有相同的权重.
(6)


(7)

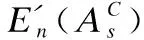

(8)
定义 6.分类型数据第s维特征上的权重ws

(9)
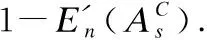
(10)

定义 7.基于熵权的分类型相异度系数
对于任意xi,ql∈D,它们之间基于熵权的分类型相异度系数定义如公式(11)所示.
(11)
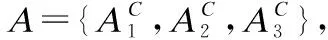
使用k-prototypes算法的相异度计算结果为:
d(x16,q1)=d(x16,q2)=0+0+0=0;
d(x16,q3)=1+0+1=2;
使用EKACMD算法的相异度计算结果为:

表3 人工数据集D2Table 3 Artificial data set D2
d(x16,q2)=1.896392;d(x16,q3)=2.836363
使用KPMD算法的相异度计算结果为:
d(x16,q2)=0.632130;d(x16,q3)=0.946240;
由上述计算可知,KPMD算法的相异度系数可以对x16进行正确的划分.
4.2 量化的数值型相异度系数
定义 8.数值型相异度系数dN(xi,ql)
令dN(xi,ql)表示混合型数据集数值型数据部分的相异度,定义如公式(12)所示.
(12)
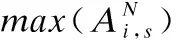
(13)
定义 9.量化的数值型相异度系数dN(xi,ql)
(14)
4.3 加权的混合型相异度系数
定义 10.加权的混合型相异度系数dw(xi,ql)
设D={xi,1≤i≤n}是待聚类的混合型数据集,该数据集有n个数对象,每个对数据象有m维特征(前p维为分类型特征,后m-p维为数值型特征),将数值型特征看作一个整体(一个向量)进行处理;将分类型特征看成p维向量处理.拿一个有p维分类型特征m-p维数值型特征的数据对象xi举例,在计算相异度的过程中,使用1个数值向量和p个分类型特征来计算,即在相异度系数过程中一共有1+p维向量参与计算.因此,对于数据集中的任意数据对象xi和xj,它们之间的相异度系数定义如公式(15)所示.
(15)
定义 11.考虑权重的目标函数Fw(U,Q)
将公式(15)中定义的相异度系数应用到k-prototypes算法的目标函数中.得到加权的目标函数Fw(U,Q),其定义如公式(16)所示.
(16)
其中,
uil∈{0,1},1≤i≤n,1≤l≤k
(17)
(18)
(19)
当目标函数Fw(U,Q)的值在满足约束条件公式(17)-公式(19)的情况下,达到极小值,此时聚类过程结束.
4.4 KPMD算法流程
KPMD算法步骤如下:
算法2.一种面向混合型数据聚类的k-prototypes聚类算法(KPMD)
输入:聚类个数k;包含n个对象的混合型数据集D;
输出:聚类完成的k个簇C={C1,…,Cl,…,Ck}
Step 1.在数据集D中随机选取k个对象作为初始簇中心Q(0)=q1,…,ql,…,qk;
Step 2.初始化过程.根据公式(1)计算数据集中的每个数据对象xi与簇中心ql之间的相异度,根据最近原则将这些数据对象分配到离它最近的簇中;
Step 3.计算数值型特征的最大最小值;
Step 4.计算每维分类型特征的权重;
Step 5.迭代过程.根据公式(15)重新计算每个数据对象xi与簇中心ql之间的相异度,根据最近原则,将xi重新分配到离它最近的簇中;
Step 6.更新簇中心,确定每个子簇中的簇中心不再发生变化,即目标函数Fw(U,Q)的值不再发生变化;如果不再变化,则算法结束,否则重复Step 3-Step 5,直到目标函数值不再发生变化为止.
KPMD算法流程图如图2所示.
KPMD算法的时间复杂度主要包括初始化阶段和迭代阶段中每次计算相异度和更新簇中心.在初始化过程中将所有数据对象划分到合适的簇所需的时间复杂度是O(nkm).根据公式(16),计算待聚类分类型数据对象与簇之间的相异度的时间复杂度是O(nsp),计算待聚类数值型数据对象与簇之间的相异度的时间复杂度是O(m-p),因此计算混合型数据的总相异度的时间复杂度是O(nsp+(m-p)).假设为所有待聚类数据对象划分合适的簇需要的迭代次数为t,n是数据集中的数据对象数,m是数据集的总特征维数,k是簇数,p是分类型特征的维数,m-p是数值型特征的维数.在通常情况下
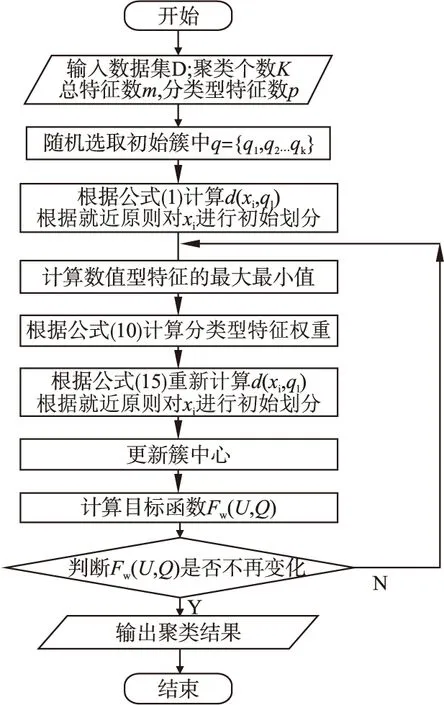
图2 KPMD算法流程图Fig.2 Flow chart of KPMD algorithm
n≫k,t,m,p,ns.则迭代过程需要的总时间复杂度是O(nkt(nsp+(m-p))).因此,KPMD算法的时间复杂度为O(nkm)+O(nkt(nsp+(m-p))).
5 实验及结果分析
5.1 性能指标
为了评估论文提出算法的有效性,论文采用指标聚类精度(accuracy,AC)对聚类结果进行评价,如公式(20)所示.NUM+表示正确分到簇Cl的对象数.聚类精度AC表示正确分到簇Cl中的对象数占总对象个数的比值.聚类正确率越高,聚类划分的正确性越高.
(20)
如果聚类结果与数据集的真实类划分越接近,AC值就越大,算法效果就越好.在下面的实验中,将论文提出的KPMD算法与Huang提出的k-prototypes算法和Sangam提出EKACMD算法进行对比实验.
5.2 实验环境
算法用Python语言实现,所有实验均在intel(R)Core(TM)处理器i7-8700K CPU@3.70GHz,Windows 10操作系统上运行.使用数据集均来自UC机器学习数据库.UCI1是加州大学欧文分校提供的专门用于机器学习的真实数据集.为了验证提出算法的有效性和可行性,论文从UCI数据集中选取Bank Marking(简称Bank),Zoo两个混合型数据集进行实验验证.选取这两个数据集作为实验数据集主要是因为混合型数据集有比纯分类型数据集和纯数值型数据集更高的复杂性.因此不可以单一的、随机的选取数据集以验证算法的有效性.选取Bank数据集做为实验数据集主要原因是为了验证在分类型和数值型特征分布均匀的情况下KPMD算法的有效性.Bank数据集的特征分布比较特殊,其分类型和数值型数据特征的个数完全一样;选取Zoo数据集做为实验数据集主要原因是为了验证在分类型和数值型特征分布不均匀的情况下KPMD算法的有效性.Zoo数据集的特征分布比较特殊,其分类型和数值型数据特征的个数差别非常大.此外,选取这两个数据集作为实验数据集的另一个原因是为了验证在数据集簇数较少和较多的情况下,KPMD算法的有效性.所选数据集的详细信息如表4所示.

表4 混合型数据集描述Table 4 Description of mixed type data set
5.3 实验结果分析
5.3.1 算法的精确度分析
实验比较了KPMD与k-prototypes,EKACMD在混合型数据集Bank和Zoo上的性能.每个算法在每个数据集上分别执行30次取平均值,聚类结果统计汇总在表5~表6中.对于k-prototypes,EKACMD和KPMD,论文分别设置k=2,k=4,k=6,k=8,k=10五种不同的聚类参数进行实验.由于EKACMD和KPMD都不需要设置聚类参数γ,因此论文只单独设置k-prototypes的聚类参数γ.
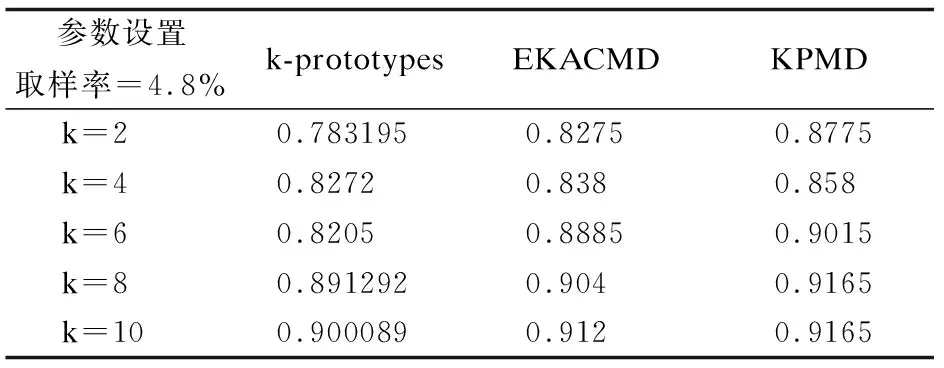
表5 银行数据集的聚类精度比较Table 5 Comparison of cluster accuracy on data set Bank

表6 动物园数据集的聚类精度比较Table 6 Comparison of cluster accuracy on data set Zoo
银行数据集有41188个数据对象,10个分类型特征,10个数值型特征,2个簇.论文对Bank数据集以4.8%的采样率进行采样.表5显示,当k=2时,KPMD的AC值分别比k-prototypes和EKACMD高9.43%,5%.
动物园数据集有101个数据对象,15个分类型特征,1个数值型特征,7个簇.表6显示,当k=7时,KPMD的AC值分别比k-prototypes和EKACMD高11.88%,4.95%.
表5和表6中的实验结果表明,就聚类精度而言,论文的算法比其他算法获得了更好的聚类结果.因为在论文算法中,簇中心的表示包含了分类型和数值型特征的分布信息.此外,论文的混合型相异度系数考虑了每个特征在聚类过程中的重要性,可以自动的计算不同特征的权重.上述原因使论文的算法可以获得更好的聚类结果.
5.3.2 提出算法与对比算法的聚类效果的直观对比
图3显示了KPMD和k-prototypes、EKACMD在不同参数k的银行数据集上的聚类精度.从图3中可以明显看到KPMD在整体上产生了良好的聚类结果,在k=4处取得最差值0.858.

图3 银行据集的聚类精度比较Fig.3 Comparison of cluster accuracy on data set Bank
图4显示了KPMD和k-prototypes、EKACMD在不同参数k的动物园数据集上的聚类精度.可以看到KPMD的曲线高于k-prototypes和EKACMD.
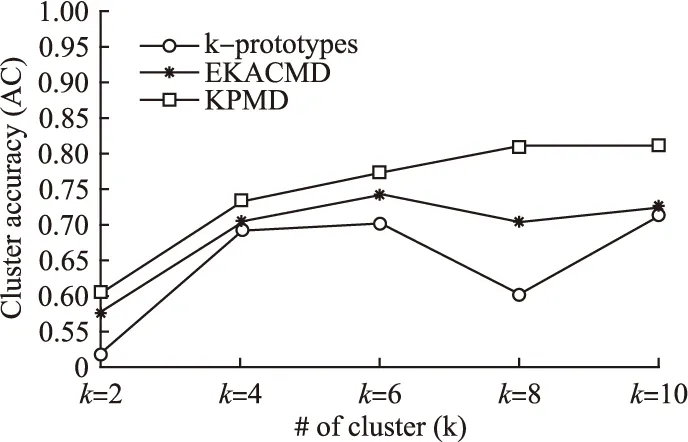
图4 动物园据集的聚类精度比较Fig.4 Comparison of cluster accuracy on data set Zoo
从图3和图4可以看出,在随机初始化的情况下,所提出的无参数算法KPMD在聚类精度方面优于k-prototypes算法和EKACMD算法.从表4所示的数据集详细信息可以看出,所选取的Zoo数据集中的分类型特征与数值型特征的个数差别很大,仅有1个数值型特征和15个分类型特征.尽管该数据集两种类型的特征分布差距很大,KPMD算法还是取得了令人满意的聚类结果.这表明所提出的混合型相异度系数适用于各种复合类型的数据集,并且不需要手动设置任何参数来调整分类型特征和数值型特征的权重.
6 结 论
k-prototypes算法是混合数据聚类中广泛使用的一种聚类算法,但聚类精度较低,聚类结果不稳定.因此论文提出了一种基于对象相异度的通用聚类框架,并通过该框架给出了统一的混合型相异度系数.对数值型数据,论文使用量化的数值型相异度系数来标准化不同的数值;对分类型数据,论文使用基于熵权的分类型相异度系数;对混合型数据,论文使用加权的混合型相异度系数.提出的混合型相异度系数不仅保留了不同类型数据的特征,还为分类型数据和数值型数据设置了合适的权重,并且基于熵理论为分类型数据内部的各个特征分配了不同的熵权,最后,论文提出了一种迭代算法(KPMD)来实现混合型数据聚类.与现有算法相比,UCI真实数据集的实验证明论文提出的相异度系数是一种更合理的混合数据聚类分析方法.总的来说,论文提出的KPMD算法不仅可以准确地找到聚类个数而且提高了聚类精度.

