一种融合评价指标相关性的多目标社区检测算法
易鑫睿,陈 昊1,,兰金明
1(南昌航空大学 无损检测技术教育部重点实验室,南昌 330063)2(南昌航空大学 信息工程学院,南昌 330063)
E-mail:18397509886@163.com
1 引 言
复杂网络将实体对象的交互关系抽象为一组顶点的连边关系,检测复杂网络的社区结构对网络犯罪、癌症监测、产品营销等现实问题具有重要意义[1,2].设计合适的社区质量评价指标是社区检测的核心问题之一.用于评价社区质量的指标,根据描述社区结构质量的角度,可以分为:基于网络拓扑特性的评价指标、基于模块度扩展的评价指标、基于节点情景特征的评价指标三类,如表1所示.
基于网络拓扑特性的评价指标,从网络内、外部连边结构对网络质量进行度量,简单易计算,包括:内部密度、平均内度、切割比、标准切割比、平均外度分数等[3];Newman等人设计的模块度指标通过网络结构强度来评价社区质量[4],至今仍是应用最广泛的指标,可以推广到无向加权网络,有向无权网络和有向加权的网络[5],之后为改进模块度存在的分辨率限制问题,扩展了包括:局部模块度函数[6]、惩罚模块密度函数[7]、Z模块度函数[8]等评价指标.第三类指标结合节点在网络图中的情景特征对社区结构进行评价,包括:单独针对网络中的顶点,量化一个顶点在分配它的社区中停留的概率,以及它被临近社区拉扯的程度的持久性指标[9]、从社区层面,考虑社区规模中每个节点和其相连的二级节点对社区贡献度的结构划分适应度[10]以及信息传播到社区内全部节点的速度为标准的紧凑度指标[11]等.
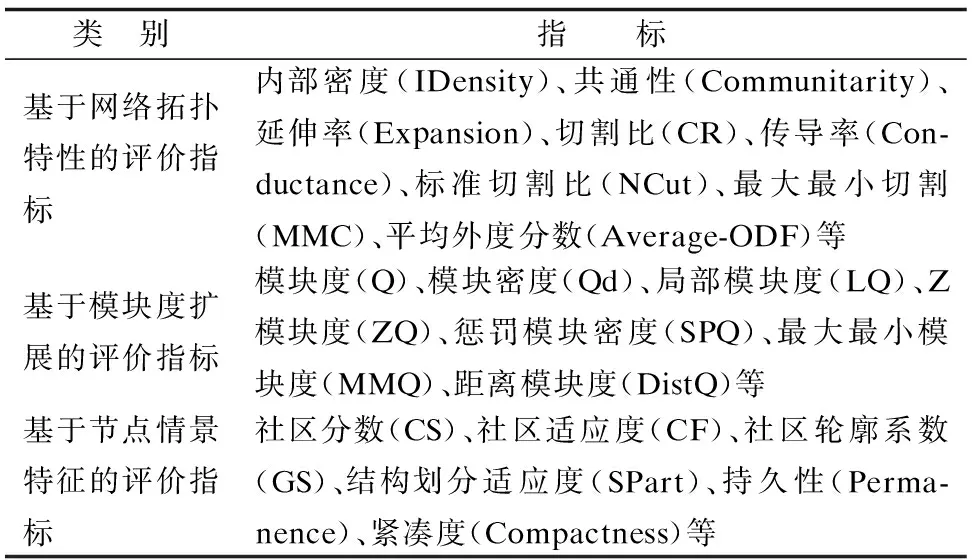
表1 社区质量评价指标Table 1 Indicators for assessing community quality
传统单目标优化的社区检测算法,检测结果受限于单一的社区结构属性.多目标社区检测算法同时选择多个评价指标,与单目标相比可以更为全面的评价社区质量,通过目标之间的权衡可以获得一组更为准确的社区检测结果.现有多目标社区检测算法有很多,其中有包括基于进化算法的MOGA-Net[12]、MOEA/D-Net[13]、NNIA-Net[14]等;基于粒子群算法的MOCD-PSO[15]、MOPSO-Net[16]等.尽管已有多种指标可供选择,但现有算法中的评价函数多依赖主观判断,严重制约社区检测的准确性与稳定性.针对这一问题,本文对社区质量评价指标间的相关性进行定义与度量,在分析目标间相关关系的基础上,构建一种新的融合评价指标相关性分析的多目标社区检测算法.
2 多目标社区检测Pareto最优解集
多目标社区检测通过优化多个度量社区结构质量的指标,以获得复杂网络中更合理的社区检测结果,其定义如下[17]:
F(Ω)=min(f1(Ω),f2(Ω),…,fr(Ω))
(1)
式中,f(·)表示第i个目标函数,Ω为已知网络G(V,E)的一种可行社区检测结果,当且仅当Ω在所有目标函数上获得最优值时,Ω被称为已知网络的绝对最优解.而在实际情况中,一般无法获得绝对最优解,通常会根据Pareto支配关系获得一组Pareto最优解.
在网络G(V,E)中,存在两种可行社区检测结果ΩA,ΩB,当满足式(2)时,称ΩA支配ΩB,记为ΩAΩB.
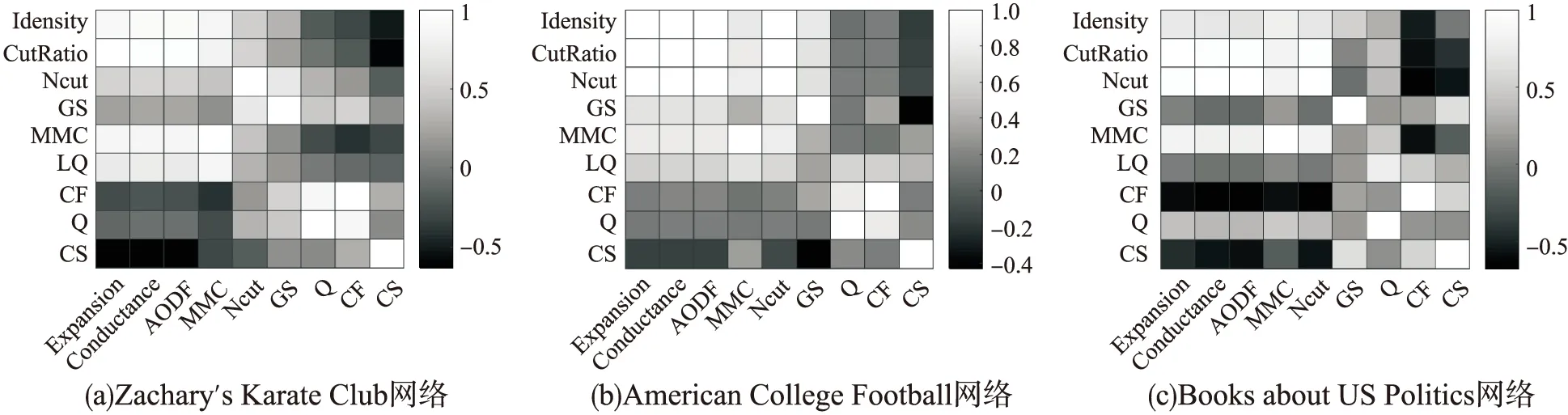
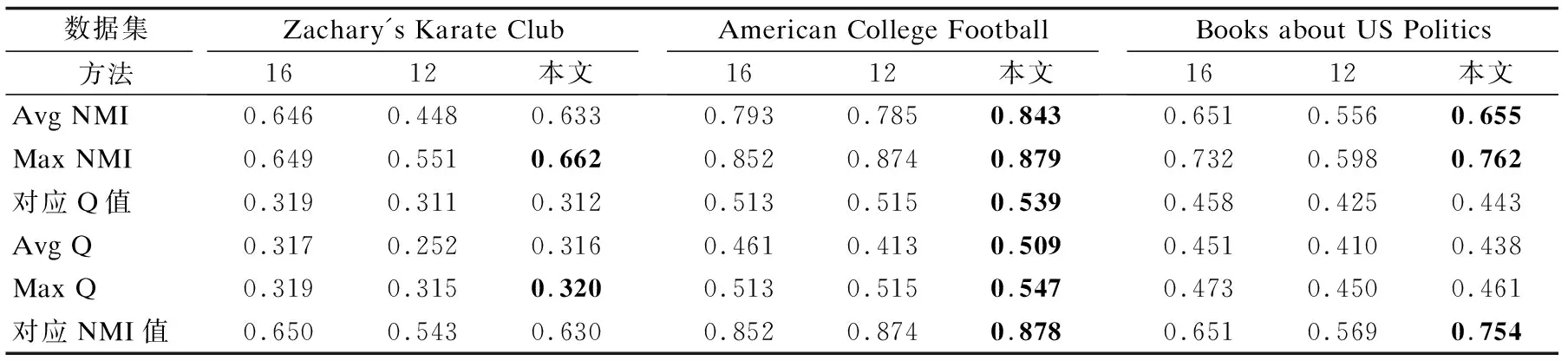
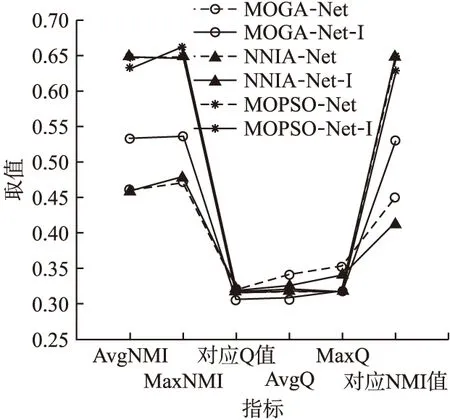
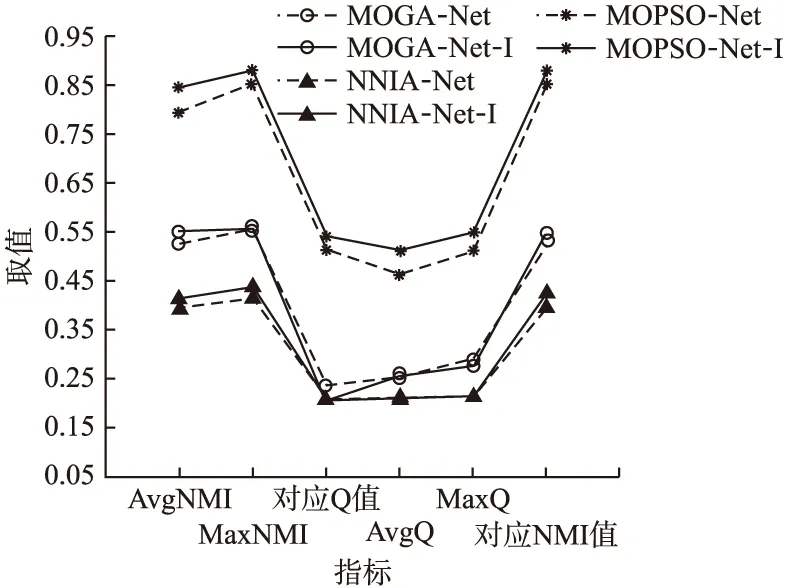
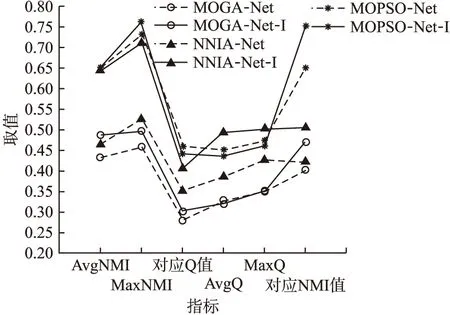
∀i:fi(ΩA)≤fi(ΩB)∧∃j:fj(ΩA) (2) 相关关系一般用于描述两个事物间存在相互作用、相互影响的关系[18].在社区检测研究中,对评价指标间存在相关关系给出如下定义. 定义1.在已知网络G(V,E)情况下,评价指标X,Y对N种不同社区结构度量结果的随机样本为(x1,y1),…,(xN,yN),如果随机变量y的取值受x的取值变化而在一定范围变化,则称Y和X之间存在相关关系. (3) 从表1中筛选部分指标,选择3个真实网络数据集验证基于Spearman系数的评价指标相关性度量方法的有效性.数据集上的随机样本数目为2000,度量结果如图1所示. 图1 评价指标之间相关性度量结果Fig.1 Correlation measurement results between evaluation indicators 观察热力图上的分布,在单个网络结构上,不同评价指标之间的相关性各不相同;在不同网络结构上,同一评价指标间的相关性存在差异.在图1(a)中,横轴上前4个评价指标与竖直方向上9个评价指标的相关性出现了较明显的分区,在分区中,Expansion等4个指标与Ncut和GS两个的相关性程度相对较低且属于正向相关影响,与CF、Q和CS则属于反向相关影响.在纵轴上,Idensity和CutRatio指标在水平方向上灰度出现渐变,其中,与横轴前6个指标属于正向相关影响,相关性逐渐减弱,与后3个指标是逐渐增强的反向相关影响.不管指标之间相关性是正向影响还是反向影响,目标函数间相关性越小,指标才能满足不同的特定目标. 比较图1(a)与图1(b)、图1(c)之间的差距.在图1(b)中,横轴上前3个度量指标在竖直方向上的分区出现了不同情况,整体呈现相关性减弱.在局部Idensity/CutRatio/Ncut与Expansion/Conductance/AODF/Ncut的相关性为1,说明指标之间在Football网络上具有等效度量能力.CF/Q两项与彼此之外的其他指标关联耦合程度相比图1(a)有所下降,平均相关性在0.18.而在图1(c)中,对比差异更加明显,相同区域评价指标之间的相关程度出现较大变化.通过以上对比实验分析说明不同的评价指标之间存在不同程度相关性,在具体多目标社区检测优化算法中,合理的选择目标函数才能保证算法获得最优解. 对以上利用Spearman相关系数度量评价指标间的相关性方法验证分析后,提出一种利用评价指标相关性模型引导求解社区检测问题的多目标社区检测算法,该算法首先利用备选评价指标间Spearman相关关系构建相似矩阵,其次,采用谱聚类算法处理相似矩阵,获得备选评价指标分类簇集,依据优选准则建模多目标社区检测问题,最后,将多目标社区检测问题与检测算法结合获得社区检测Pareto解集,通过不同准则决策获得最终社区检测结果. 多目标社区检测算法的各子目标从不同方面评价社区质量,相关性高的子目标之间实际具有等效的评价标准,按照相关性对备选评价指标分类后,更有利于选择多个不同评价标准的指标.利用谱聚类算法对备选评价指标进行分类,通过构建评价指标间的相似矩阵Wm×m,对相似矩阵进行处理,达到满足类内相似度最大,类间相似度最小划分的目的.传统相似度的计算公式以任意两样本点间的距离度量,但本文提出采用Spearman相关系数作为衡量评价指标相似度标准. 具体而言,采用第3节所提出的相关性度量方法获得备选评价指标间相关关系,将所有结果组成相关矩阵Pm×m,m是备选评价指标数目.矩阵Pm×m为对称矩阵,矩阵元素ρij的符号表示子目标i与子目标j的相关方向,数值表示子目标i与子目标j的相关性. (4) 按照评价指标组合聚类的簇类数目,提出以下两条优选准则选择评价指标,构建社区检测的多目标问题. 准则1.在任一簇内,如果当前备选评价指标与簇内其他备选评价指标之间的相关性均值fI最大,则当前备选评价指标作为目标之一被选择. 准则2.在任一簇内,如果最大相关性均值存在多个备选评价指标,则备选评价指标与簇外其他备选评价指标之间的相关性均值fII最小者被选择作为目标之一.关于相关性均值计算公式如(5)所示. (5) 根据前面组合聚类与优选准则从备选评价指标集构建多目标社区检测问题的方法流程伪代码如下所示: 方法.多目标社区检测问题构建方法MOCDP 输入:网络G(V,E),备选评价指标集合f={fi,i=1,…,m},优选评价指标数目r 输出:优选评价指标集合f′={fi,i∈1,…,m;|f′|=r} 1.初始化可行社区检测结果数据集Set={Ω1,Ω2,…,ΩN}; 2.fort=1:mdo 3.计算产生备选评价指标ft的随机样本点Ft={ft(Ω1),ft(Ω2),…,ft(ΩN)}; 4.F=F∪Ft;//F是由样本点组成的随机变量空间 5.endfor 6.fort1,t2=1:mdo 8.endfor 9.计算度矩阵D; 10.计算拉普拉斯矩阵Lm×m=D-P′; 11.计算Lm×m的k个特征向量组成Vm×k={v1,…,vk}; 12.(c1,…,cr)=Kmeans(Vm×k,r); //相关性聚类 13.forj=1:rdo 14.ifmax(fI(i),i∈cj)==1then 15.f=f∪fi; //按照准则1选择fi作为目标函数 16.else 17.fi=min(fII(i),i∈cj); 18.f=f∪fi; //按照准则2选择fi作为目标函数 19.endif 20.endfor 21.returnf′={fi,i∈1,…,m;|f′|=r} 优选获得评价指标指导多目标社区检测算法处理具体复杂网络,能使Pareto解集包含更多社区质量特征,满足不同决策需求,依据决策准则获得最后结果.结合优选评价指标的多目标社区检测算法具体实现步骤如下: Step 1.建立复杂网络G(V,E),设置种群规模popsize,最大迭代代数Maxiter; Step 2.构建备选评价指标集合f={fi,i=1,…,m},产生可行社区检测结果集合Set; Step 3.按照多目标社区检测问题构建方法MOCDP,构建f′={fi,i∈1,…,m;|f′|=r}; Step 4.初始化种群Pop,开始循环优化iter=1; Step 5.计算种群个体适应度值p=(fi(Ωp),fi∈f′); Step 6.比较种群支配关系,获得Pareto占优种群; Step 7.根据多目标社区检测算法操作算子对种群Pop进行更新; Step 8.重新计算种群适应度值,更新Pareto占优种群; Step 9.若满足最大迭代条件iter>Maxiter,结束输出Pareto占优种群,否则,返回执行Step 7; Step 10.依据决策准则从Pareto占优种群选择最终结果. (6) 通过对融合评价指标优选的多目标社区检测算法结果质量进行度量,可以反映评价指标优选对算法的影响.本文在度量多目标社区检测算法结果质量时,选择模块度函数Q和归一化互信息函数NMI. 模块度函数Q在优化算法中不仅可以作为目标指导种群进化,而且也常应用于度量结果质量,在4.3节已经具体说明.归一化互信息函数NMI[20]是在已知网络真实社区结构的前提下,用于度量网络社区检测结果和真实社区结构之间的相似性,相似性越高说明算法准确性越高.NMI的定义如下: (7) A和B分别为算法在网络G(V,E)上的检测结果和实际真实社区结果,CA(CB)是网络社区划分数目,C为混淆矩阵,C中元素Cij为中第i个社区与B中第j个社区的共同节点数目,Ci·(C·j)则表示混淆矩阵C中第i行(第j列)元素总和,N是网络的节点数目.如果A=B,则NMI(A,B)=1;如果A和B完全不同,则NMI(A,B)=0. 实验所选用的网络数据集包括Zachary′s Karate Club网络、American College Football网络、Books about US Politics网络3个真实网络数据集,各网络数据汇总如表2所示. 表2 网络数据集数据汇总表Table 2 Network dataset data 5.2.1 MOCDP方法构建多目标社区检测问题结果 共收集19种备选评价指标用于优选构建多目标社区检测问题,如表3所示.依据指标间相关性的聚类操作,每个数据集上获得的结果如表4所示. 表3 备选子目标集合汇总表Table 3 Alternative sub target set 表4 构建多目标社区检测问题结果汇总表Table 4 Build multi-target community detection problem results 5.2.2 不同目标组合对多目标社区检测算法性能影响 本文为分析MOCDP方法构建的多目标社区检测问题对于社区检测算法的性能影响,在MOPSO-Net[16]算法框架基础上,将文献[12]与文献[16]中选择的目标函数组合与采用MOCDP方法产生的目标函数组合进行了对比实验.参数设置按照MOPSO-Net中说明,在三个真实网络数据集上运行20次的实验结果如表5所示. 观察三个数据集上整体实验结果发现,基于本文MOCDP方法的MOPSO-Net算法能够取得有效的实验结果,说明MOCDP方法用于构建社区检测算法的多目标问题可行.而与此同时,可以发现不同目标组合方法指导MOPSO-Net寻优的效果在不同数据集上存在较大差异,如文献[12]中选择CS/CF指导MOPSO-Net寻优时更明显,表现在Football网络上结果更好,在Club网络上结果更差,说明在多目标社区检测处理问题时,合理选择目标函数组合十分必要. 分析MOCDP方法对MOPSO-Net寻优的影响,在处理同样网络数据集时,本文优选的目标指导MOPSO-Net算法寻优效果更好,特别在Football网络结构中,本文优选的目标函数组合是MMC/CF,获得的社区检测结果在NMI值与Q值两项指标的多次实验的最大均值与最大值都超过了另外两种目标组合结果.在Politics网络数据集上,三种组合的目标函数获得的Q值的最大均值与最大值相近,但本文MOCDP方法的优选目标组合Compactness/CS获得的检测结果NMI值更优. 表5 不同多目标组合在MOPSO-Net处理不同数据集上的实验结果Table 5 Experimental results of different multi-target combinations on different data sets processed by MOPSO-Net 对于应用同一目标函数组合处理不同网络数据集时,多目标社区检测算法寻优结果之间存在效果差别.如Club网络中,三种目标函数组合方式指导MOPSO-Net算法寻优时,普遍效果较差,而在Football网络中则普遍更好,分析原因是网络数据集的复杂度影响,网络中反映社区特征少而影响到目标函数对种群解个体的评价,致使寻优效果不好.但综合整体实验结果,本文MOCDP方法构建的多目标社区检测问题在相同算法中检测效果更好,能够发现与网络真实社区结构更相近的社区检测结果. 5.2.3 结合MOCDP方法的不同多目标社区检测算法性能分析 为验证本文MOCDP方法在不同算法上的结果影响,以下选择MOGA-Net算法、NNIA-Net算法、MOPSO-Net算法设置实验.其中,需要说明的是MOGA-Net算法中,交叉操作与变异操作的概率分别设置为0.8和0.2,采用轮盘赌选择的精英个体设置为种群规模10%.每个算法在同一网络上的种群规模设置为1000,进化代数1000代,实验算法的其他参数依据相应原文献设置,重复运行20次,获得算法结果统计如图2、图3、图4所示. 图2 在Zachary′s Karate Club网络上比较更改目标函数前后不同算法性能Fig.2 Compare the performance of different algorithms beforeand after changing the target function on Zachary′sKarate Club network 由图上显示,在相同网络上,运用MOCDP方法优选目标函数后,不同多目标社区检测算法获得结果之间存在不同差距.图2中,MOGA-Net算法和NNIA-Net算法相比MOPSO-Net算法更为明显,原有平均最大NMI值分别为0.46和0.459,平均最大模块度值分别为0.341和0.325,优选目标函数后,MOGA-Net-I、NNIA-Net-I算法在性能上出现提升,特别是,NNIA-Net-I算法在多次运行结果中,每次结果的最大NMI值与最大模块度值Q保持稳定,获得统一的网络社区划分结果.MOPSO-Net-I算法虽然平均最大NMI值和平均最大模块度值Q在结果上不及原算法,但实验结果中最大NMI值和最大Q值分别优于原算法. 图3 在American College Football网络上比较更改目标函数前后不同算法性能Fig.3 Compare the performance of different algorithms beforeand after changing the objective function on the AmericanCollege Football network 比较图3中结果,虽然MOGA-Net-I获得的最大NMI值和最大Q值略低MOGA-Net,但两项指标在均值上更优,说明MOGA-Net-I算法结果更为稳定,解集合整体质量更优秀.此外NNIA-Net-I结果中NMI值指标与Q值指标基本和原算法一致.而图4中结果显示所有算法对Politics网络数据集进行社区检测时,最大NMI值均在0.4以上,而NNIA-Net-I的最大NMI值达到0.712,与NNIA-Net的0.524相比提高35.87%.虽然MOGA-Net-I与MOPSO-Net-I相比原算法获得的结果模块度值Q有所下降,但平均最大值NMI值均有提高. 当相同算法处理不同网络数据时,通过MOCDP方法优选目标对同一多目标社区检测算法性能的影响程度存在差异.实验结果表明在三个真实网络数据集上采用MOCDP方法优选目标函数能够提升多目标社区检测算法性能,其中,MOCDP方法优选目标函数效果在MOGA-Net、NNIA-Net算法上更好.说明采用MOCDP方法优选目标函数有助于提升多目标社区检测算法准确性性能,并且在不改进算法框架的前提下,合理优选目标函数使得社区检测算法结果稳定性提高,网络社区划分结果更满足决策需求. 图4 在Books about US Politics网络上比较更改目标函数前后不同算法性能Fig.4 Comparing the performance of different algorithmsbefore and after changing the objective function on theBooks about US Politics network 针对复杂网络中社区检测算法的研究,提出一种基于评价指标相关性分析的多目标社区检测算法.首先介绍了已有度量社区质量指标的三种分类,定义评价指标的相关关系,通过基于Spearman相关系数的目标相关性度量方法,对目标函数之间关系进行验证分析,随后,在介绍基于评价指标相关性分析的多目标社区检测算法时,详细描述了评价指标组合聚类操作步骤,提出了评价指标优选准则与MOCDP方法伪代码内容.将MOCDP方法在三个真实网络数据集上进行实验,构建了不同的多目标社区检测问题.选择了MOPSO-Net算法框架,对比已有的两种目标函数组合与MOCDP方法对相同算法的结果影响,实验表明,同一算法框架下,MOCDP方法选择的目标函数组合更有利于算法寻找最优解.与此同时,MOGA-Net,NNIA-Net,MOPSO-Net三种不同算法在结合MOCDP方法之后,算法有效性出现不同程度的提升.本文考虑已有算法框架的寻优性能不足问题,下一步将结合以上研究内容设计一种更具应用价值的新的多目标社区检测算法.
3 评价指标间的相关性分析
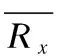
4 结合评价指标相关性分析的多目标社区检测算法
4.1 评价指标组合聚类
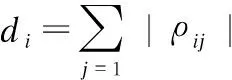
4.2 评价指标优选准则与方法描述
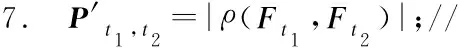
4.3 结合优选评价指标的多目标社区检测算法

5 实验与分析
5.1 实验结果度量标准
5.2 实验数据及结果


6 结 论

