基于机器学习的室内定位技术研究

郭正硕，徐舒敏，吴锦州，华 胜

（1.南京邮电大学 物联网学院，江苏 南京 210000；2.南京邮电大学 计算机软件学院，江苏 南京 210000；3.南京邮电大学 通信与信息工程学院，江苏 南京 210000）

当前，室内定位的实现方案很多，基于无线局域网（Wireless Local Area Networks，WLAN）的定位方法主要有三角形算法和位置指纹识别。三角形算法利用最少3个已知无线接入点（Access Point，AP）之间的距离信息估计目的坐标，其中，距离是通过测量来自AP的接收信号强度（Received Signal Strength，RSS）进行估计，而基于三角形算法的WLAN定位在不同环境下的传输损耗大不同，所以也很难建离精准、合适的损耗模型[1-2]。因此，基于三角形算法的定位方法在实施过程中困难重重。

WLAN具有高精度、低成本、可移动的优点，本项目基于机器学习算法，使用Matlab软件，应用Hankel矩阵和自适应卡尔曼滤波技术，将噪声信号在指纹数据库中进行过滤，实现离线和在线的室内定位。离线阶段和在线阶段共同处理，既能在指纹数据库上更好地降噪，又能提高算法的定位精度。实现方案经过实验数据检验，具有精度上的可靠性。

离线阶段的主要任务是构建一个指纹识别数据库，本文构建指纹数据库的Hankel矩阵，利用信号空间和噪声空间奇异值不同的特点，可以有效去除部分噪声，重构成较为精确的指纹数据库，以供在线阶段比对。

与传统矩阵恢复算法相比，本文所提出的基于Hankel矩阵的方法在计算复杂度和降噪性能方面具有优势。Hankel矩阵在从左到右的每个上升斜交对角线中具有相等的元素，可以通过适当的奇异值阈值，仅通过一个奇异值分解，就将信号空间与噪声空间分开。基于奇异值的分解降噪是一种分析非线性、非平稳信号的有效方法，由于Hankel矩阵结构具有特殊性，可以有效地将噪声与需要的信号分离、提高信噪比，并且能保留与噪声信号的频谱相混叠的系统信号。

在线阶段，用户终端测量来自所有AP的RSS，并将其与指纹数据库中信号强度空间的RSS进行比对，用合适的指纹匹配算法计算用户的位置。广泛使用的指纹匹配算法是WKNN算法，但传统的WKNN算法存在一定的局限性，会影响定位精度，需要进行改进。

Luo等[3]指出RSSI概率分布呈现一定的高斯分布特性，朱雪梅等[4]在其基础上提出了一种基于RSSI分布重叠相似度的WKNN室内定位方法，即利用RSSI高斯概率分布重叠相似度与距离之间的关系，设定相似度阈值选取k个近邻指纹点作为取样点，以此获取定位结果，解决传统最大相似度法可能带来的较大误差和定位时间较长等问题。但实际上，参考点上信号强度分布并不是一个标准的高斯分布，还受到各种干扰的影响，因此，需要考虑各AP信号强度之间的关系。陈淼[5]认为，AP信号强度大小主要受到AP信号发射稳定性带来的影响。在此基础上，本文基于方差进行改进算法，降低AP信号发射稳定性带来的干扰，进一步提高定位的精度。

本文在指纹数据库构建阶段，基于Hankel矩阵的特性、真实信号空间和噪声空间奇异值不同，通过特征均值法设置阈值，对离线阶段的指纹数据库进行降噪处理，提高了离线阶段指纹数据库的精确度。同时，提出了一种提高定位精度的方法，主要分为两步：第一步，利用自适应滤波方法，降低定位系统外部环境变化带来的干扰。第二步，对自适应滤波过滤后的指纹数据库使用基于方差改进的WKNN算法，降低定位系统内部AP发射功率稳定性带来的影响。利用各取样点在不同的AP下测得的方差设置权值，为不同的RP坐标分配权重，有效地降低了AP波动带来的干扰，提高了现有WKNN算法的定位精度。

1 离线阶段指纹数据库的构建

1.1 Hankel矩阵奇异值分解原理

假设存在矩阵M为m×n阶，其中的元素均属于R或者C。则存在一个分解使：

其中，U是m×m阶幺正矩阵，∑是半正定m×n阶对角矩阵；而V*是V的共轭转置矩阵，是n×n阶酉矩阵。此分解法称为矩阵的奇异值分解。对Hankel矩阵H进行奇异值分解得到：

式中，Um×m和Vn×n为正交矩阵，∑m×n为非对角矩阵，为矩阵H的奇异值。保留前K个奇异值而剩余则置零，再利用奇异值分解的逆过程得到重构矩阵H_s，将H_s依据空间重构的方法得到降噪后的信号。

本文假设信号与噪声空间互不相干、奇异值不相同、信号空间较为集中，而噪声空间相对而言较为分散，根据这些特点设置合适的阈值，将信号与噪声分离。

1.2 离线阶段指纹数据库处理

1.2.1 含噪指纹数据库到Hankel矩阵处理原理

假定含噪指纹数据库包含位置空间和信号强度空间的映射关系，其中，位置空间由所有参考点（RP）的位置构成，信号强度空间由RP从AP测得的一系列接收信号强度（RSS）值构成，每个RP的位置对应一组来自所有AP的RSS值。

将所有参考点来自同一AP的RSS向量构成Hankel矩阵H。为了实现信号和噪声的充分分离，构造的Hankel矩阵行数m和列数n的乘积应尽可能地最大。满足行数m和列数n的最大乘积主要取决于信号个数的奇偶性，所以，根据N的奇偶性和不等式原理来确定矩阵行数m。刘佳音等[6]研究发现，当N为奇数时，m＝（N＋1）/2；当N为偶数时，m＝N/2，式中，N为信号个数，n由等式n＝N＋1－m来确定。

从含噪声指纹库中提取第i（1≤i≤N）个RP对应的来自各个AP的RSS值组成的信号矢量Xi，将Xi构造成Hankel矩阵Hi。

一个Hankel矩阵H可以表示为由一个信号空间Hs和一个噪声空间Hn构成：

1.2.2 Hankel矩阵降噪原理

基于奇异值分解的信号降噪方法基本思路：根据真实信号和噪声的不同特征，将含噪的测量信号构成的Hankel矩阵分解成真实信号空间与噪声空间，利用不同的奇异值选择方法对两个空间的奇异值矩阵处理后重构信号，即可有效抑制测量信号中的噪声。

对Hankel矩阵H进行奇异值分解，得到对应关系为：

式中，U和V为正交矩阵，而∑为非对角矩阵[6]。此方法的关键是恰当地选择矩阵H的奇异值，将信空间Hs和噪声空间Hn分开。设Hs的秩为rs，Hn的秩为rn。

假设理想信号s（k）和噪声n（k）不相关，并且信号空间Hs的最小非零奇异值σsrs大于噪声空间Hn的最大奇异值σn1，则可以得到以下结果：

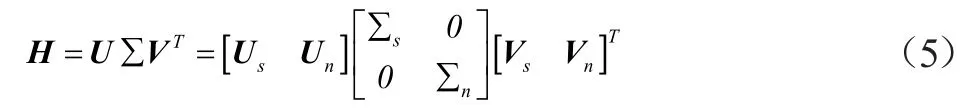
其中，H=Hs+Hn。以外积的形式重公式（6）：

可以得到：r＝rs＋rn。

比较式（6）和式（7）可以看出，从∑中选择恰当的奇异值，便可以将噪声从信号空间中分离。假设选择前l（=rs）个奇异值作为估计的理想信号空间，那么H可以被分成估计的理想信号空间，和估计的噪声空间，形式如下：

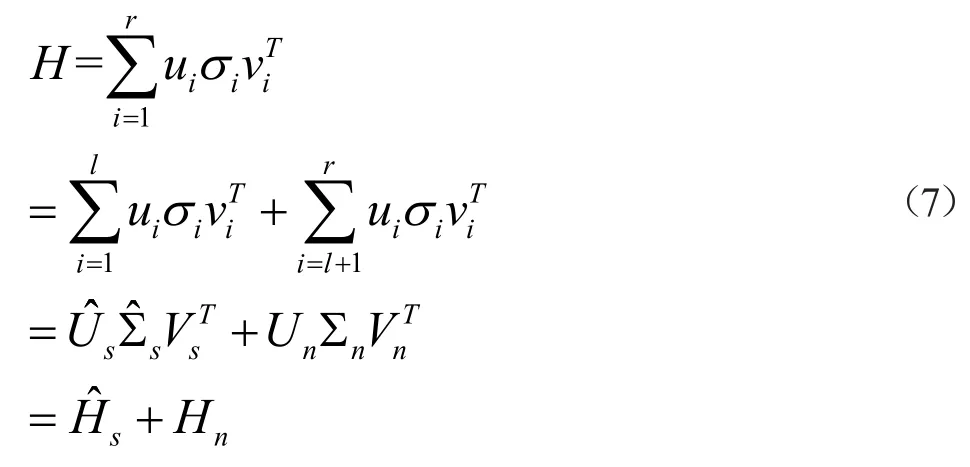
确定奇异值选择方法，进而选择奇异值个数，然后对奇异值矩阵∑进行处理，∑'为处理后的矩阵；利用U，V和∑'构造新的矩阵

奇异值阈值的选择在降噪过程中起到了决定性的作用，本文选用特征均值方法，在含噪的Hankel矩阵奇异值分解后，设得到的奇异值为σi，是方阵AAT的特征值λi的平方根，即：

将小于全体特征值均值的特征值置零，可以实现奇异值个数的准确判断；然后重构矩阵，实现信号的降噪。

1.2.3 Hankel矩阵恢复原理

根据Hankel矩阵的特性，降噪得到的理想信号空间同样是Hankel矩阵，因此，可以很方便地将对应AP的指纹数据库恢复[8]。

抽取中每一条副对角线的平均值s来重建所需要的信号序列s（k），s（k）可以表示如下，n为矩阵的列数：

对所有AP的信号向量，可以得到所估计的信号向量（i=1，2，...，M，M为矩阵行数），最后，将所有的按照顺序排列，即可得到降噪后的指纹数据库：

通过对每个Hankel矩阵中副对角线上的元素取平均值来减小误差，完成了利用Hankel矩阵奇异值分解来对指纹数据库进行的降噪处理。

2 Sage-husa AKF的应用

2.1 自适应滤波技术

在本项目中，室内是一个动态变化的系统。为了将新指纹数据库与在线RSS进行比对，在收集信号时对于RSS信号的噪声过滤尤为重要。

由于在大多数实际系统中，系统过程噪声方差矩阵Q和量测误差方差阵R无法预知，量测矩阵H和状态转移矩阵也难以确立。如果建立的模型与实际模型有出入，则会引起滤波发散。自适应滤波方法可以有效解决滤波发散，使用量测值对预测值进行修正，也对不确定系统模型中的参数和噪声统计参数进行估计修正。在线算法中AKF的使用如图1所示。

图1 在线算法中AKF的使用

自适应滤波是一种最佳滤波算法，在维纳滤波、普通卡尔曼滤波的基础上发展出了更强的适应性和更好的滤波效果，在实际应用中，尤其是在信息处理方面，得到了较好的发展[9]。

2.2 自适应卡尔曼滤波

关于自适应卡尔曼滤波，目前，使用较多的一种方法是Sage-Husa自适应滤波算法。该滤波方法在使用量测数据进行递推时，通过时变噪声估计估值器，实时估计和修正系统噪声和量测噪声的统计特性，从而修正系统模型误差，并且在一定程度上抑制滤波发散现象。现假设线性离散系统数学模型为：

其中，Xk为系统状态向量，Φk|k－1为系统状态转移矩阵，Γ为系统噪声矩阵，Wk为系统噪声向量，Zk为系统观测向量，Vk为量测噪声向量。

基于数学模型设计的sage-husa自适应滤波算法如下：

其中，式（13—14）对应预测部分，对状态量X和伴随协方差P进行预测，得到X'和P'。

式（15）为自适应卡尔曼滤波引入的一个超参数，调节更新参量dk，b被称为遗忘因子，取值在0.95～0.99之间。式（16—19）对应更新部分的增益系数K求导部分，主要区别在于观测误差R基于dk帧数k变化，Rk→Rk－1，即观测误差R趋向稳定。

式（20—21）对应更新部分的状态量更新部分需要注意的是，如果系统状态变量的维数比较高，而Sage-Husa AKF中又增加了对系统噪声统计特性的计算，计算量将大大增加，实时性也将难以得到保证。对于阶次较高的系Sage-Husa自适应滤波算法中Rk和Qk的在线估计，有时会由于计算发散失去半正定性和正定性而出现滤波发散现象，此时，Sage-Husa自适应滤波算法的稳定性和收敛性不能完全保证。

3 基于方差改进的WKNN算法

3.1 基于欧式距离的WKNN算法的局限

在使用欧氏距离进行相似性计算时，RSS信号的强度反映了物理距离的远近，理想情况下为物理位置越接近的点，RSS之间的差值就越小。由于室内是一个动态变化的系统，采样点上采集到的RSS会有一定程度的波动，而对发射信号功率稳定性差的AP，波动尤为明显。在实际情况中，信号强度的差值不一定完全由物理位置的远近造成，也可能由AP自身的波动造成，使得欧氏距离为近邻算法的权重时并不能真实反映实际的物理距离。因而需要对在基于欧式距离的近邻算法进行改进[10]。

3.2 改进WKNN算法

与传统的WKNN算法相比，改进的WKNN算法在离线阶段对多次测得的信号强度取方差，方差反映样体数据分布的离散程度，方差大的采样点，RSS的波动越大，样本集中的样本点与均值差异较大的可能性也越高；方差小的采样点，RSS的分布越集中，任意时刻的信号强度都不会脱离均值太远。将方差的倒数作为系数加人到距离的计算中，降低方差大AP的接收信号强度在距离计算时所占的权重，使用加权欧氏距离进行相似性计算时，能在一定程度上消除部分RSS波动带来的影响，提高最终的定位精度。

3.2.1 方差特征的提取

在离线阶段建立指纹库时，为了使指纹库中每个采样点的特征更为真实地反映对应物理位置的RSS特征，会在每个采样点上进行多次的样本采集。每个采样点接收到每个AP的信号强度都是一个样本集，包含在该点多次采集的信号强度。如采样点j接收到第t个AP的信号强度信息集为：

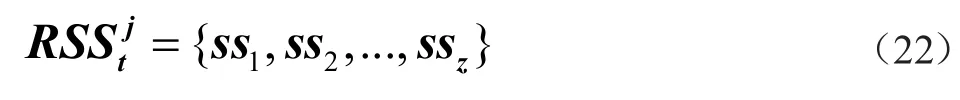
其中，Z为每个采样点的样体量。指纹库中任意采样点j的RSS向量为：

其中，N为AP的个数。由此，得到接收信号强度rssj和接收信号方差σ j的向量：

3.2.2 加权距离的计算

加权欧氏距离是针对简单欧氏距离缺点的一种改进方案，相当于为n维向量的不同维度赋予了不同权重，权重与该采样点RSS的方差相关，使用加权距离计算待定位点i与采样点j的距离dij：

4 仿真结果

本团队模拟了一间30×30 m的房间，在房间的4个顶角模拟4个AP，并选取957个RP，相邻RP之间的距离为1 m。使用的室内信道传播模型和RP测得的RSS值分别表示如下：

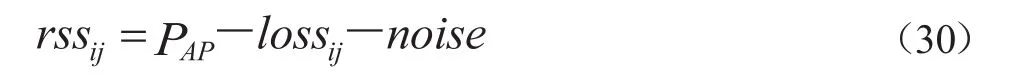
其中，lossij表示第i个AP到第j个RP的功率损耗，disij表示第i个AP与第j个RP之间的距离，i=1,…,4，j=1,…,957。PL(d0)是在参考点d0处的功率损耗，本文中d0为2 m。Gr和Gr分别是发送天线增益和接收天线增益，Gt＝Gr＝1。是自由空间，c是光速，f是载波频率，f＝2.4×109Hz。n是信道衰减因子，其范围在2～5之间，n＝2。rssij表示在第j个RP测得的第i个AP的RSS值，PAP表示AP发射功率，如无特别说明，PAP＝30 dBm，noise是均值为0、方差为0.1的高斯白噪声。

在离线阶段，基于式（28—29）在所有RP处多次模拟接收来自所有AP的RSS值，对模拟结果取平均值，构建指纹数据库，供在线阶段使用。在在线阶段，测试点测得的RSS值由同样的模型模拟产生。

本团队使用两种方法来评估定位精度：

（1）使用测试点的位置估计与其实际位置之间距离的均方根误差（RMSE，单位：m）来评估：

（2）使用定位误差的概率分布来评估。

在仿真的离线阶段，根据模拟的初始指纹数据库构建Hankel矩阵，通过仅一个奇异值分解，就可以设置适当的奇异值阈值，将信号空间与噪声空间区分开，以此过滤掉部分噪声。利用不同的奇异值选择方法对两个空间的奇异值矩阵处理后，重构信号组成指纹数据库。

降噪后，将降噪前后的RSS值进行对比。通过离线阶段的信号空间分解，可以为在线阶段信号位置的比对提供更加精准的信号定位点，受噪声的干扰较小，相比较只在在线阶段进行过滤降噪的方法有了更进一步的突破。

标准KF算法、Sage-Husa AKF算法的降噪效果对比如图2所示，其中，横坐标为算法的迭代次数，纵坐标是每一次迭代运算之后获得的降噪后的RSS数值。

可以看出，标准KF算法的迭代过程不收敛，偏差原RSS测量值较大。本文Sage-Husa AKF算法相较于标准KF算法更加接近RSS测量值，但在某些时刻的迭代过程中，RSS波动较大，会偏离RSS测量值，也验证了其缺点所在。标准KF算法过于简单，在降噪的过程中无法适应信号和噪声的统计特性，Sage-Husa AKF算法在标准KF算法的基础上加入遗忘因子b以及噪声协方差估计，利用前一时刻的降噪输出结果，调节现时刻滤波参数，相较于标准KF算法能更好地适应信号与噪声的统计特性。不降噪时与Sage-Husa AKF算法降噪定位性能RMSE的对比结果如表1所示。

表1 降噪方法使用效果

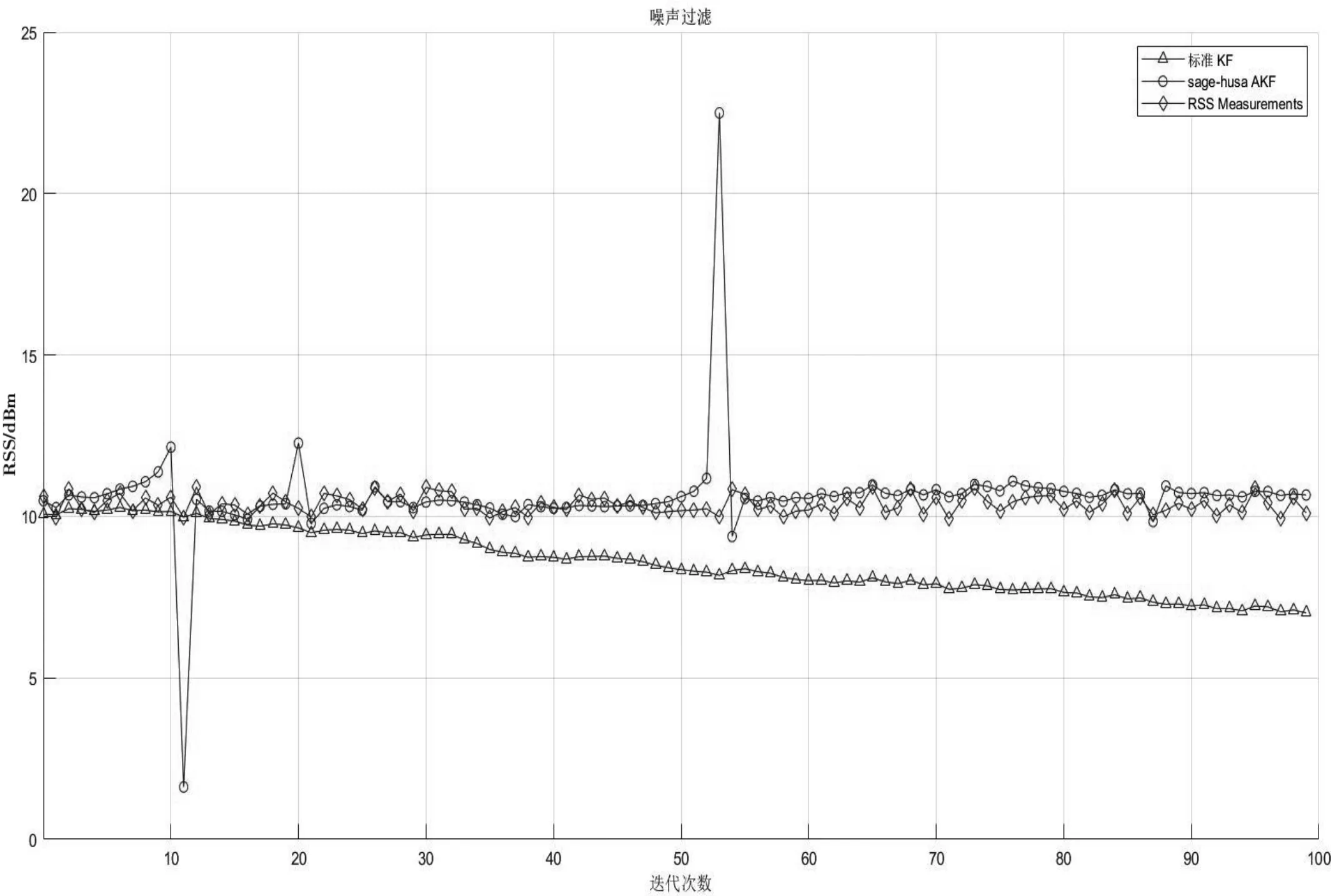
图2 标准KF算法与Sage-Husa AKF算法

为了验证改进WKNN算法对定位效果的提高作用，对所有测试点的定位误差进行统计，定位误差累积分布函数如图3所示。累积分布函数能描述变量的概率分布情况，表示变量小于或等于某个数指的概率，定位误差累积分布曲线上的点表示定位误差小于x的概率。

图3 一般WKNN与改进WKNN定位效果对比

可以看出，基于加权距离的改进WKNN算法的定位效果优于一般的WKNN算法。

仿真时采样点单次测量的信号强度标准差设置为在一个略大范围内随机提取，由此模拟AP信号不稳定的情况。从仿真结果的分布上看，改进的WKNN算法的误差集中在1～2.5 m的区间，几乎没有3 m以上的误差，相较于对同一仿真数据所使用的一般WKNN算法，本论文提出的改进WKNN算法有较为明显的提升。由此可以得出，当使用的AP信号较不稳定时，基于加权距离的改进WKNN算法的定位效果优于一般的WKNN算法。

5 结语

由于在室内环境中受到的环境影响因素较复杂，在建立指纹书库过程中难以避免地会引入许多噪声信号。本文在研究室内定位技术的过程中，提出了基于Hankel矩阵的降噪方法，关键部分是分为离线阶段和在线阶段，通过两部分不同的功能来进行去噪。在离线阶段，主要任务是利用Hankel矩阵构建一个指纹识别数据库，是指纹识别方法的基础，因为保留了信号空间和位置空间之间的映射。在在线阶段，用户终端感测RSS，并进一步将其与指纹数据库的信号空间匹配，以估计用户位置。在线阶段使用sage-husa AKF进行滤波后，使用改进WKNN算法提高定位精度。