基于等效迎角的气动融合轨道直接积分计算无控航天器轨道衰降研究

党雷宁，李志辉，2*，唐小伟，梁 杰，彭傲平

（1.中国空气动力研究与发展中心超高速空气动力研究所，绵阳621000；2.国家计算流体力学实验室，北京100191）

1 引言

低地球轨道（1000 km高度以下）运行的航天器的轨道高度因大气阻力而衰减。尤其当航天器处于300 km高度以下的超低轨时，大气密度急剧增加，空气动力引起轨道的衰降更加显著。考虑航天器超高速飞行过程空气动力对轨道模拟计算的影响，不仅对航天器寿命末期可能的再入预警、陨落坠毁分析意义重大，而且是低轨航天器轨道设计和维持的重要研究手段。轨道衰降和再入点预报的准确程度，直接影响航天器再入时间、损毁和落区预报的准确程度。目前无控航天器陨落预报依靠测站轨道星历数据支撑阻力系数的拟合及外推，精度较低，长期预报误差可达数月，临近陨落期预报精度约为1 h～10 min［1］。

大气阻力对轨道高度的影响有2个方面［2-3］：①沿飞行轨道的热层大气总质量密度；②航天器的空气动力特性，特别是阻力系数。自20世纪60年代以来，研究人员发展了Jacchia、MSIS系列、JB-2008等高层大气模式［2，4］，极大地提高了热层大气密度预测的精准度。但对于轨道预报，现有的大气模型在描述实际的大气密度变化上还存在较大误差，并依赖辐射流量和地磁指数的预报值［5］。

在轨航天器空气动力系数是航天器外形、飞行高度、速度和飞行姿态的函数［3］。当这些影响因素确定后，可通过地面试验和数值模拟等稀薄气体动力学研究手段，获得准确的空气动力特性［6-8］。在其它因素都确定或者变化小的情况下，飞行姿态对空气动力系数影响很大。当航天器正常工作、飞行姿态稳定，往往可以预测得到较准确的气动力系数。如果航天器处于无控状态，飞行器自旋，飞行姿态不确定性大，空气动力系数的预测将十分困难。

大气密度和空气动力系数预测模型较大的误差，使得失效航天器轨道衰降无法得到准确的预报，预报时间越长，误差越大。Tapley［9］、Montenbruck等［10］较多地依赖于数值手段，通过引入各种待估参数来克服大气密度和阻力系数的不确定度。苍中亚等［11］采用TLE轨道根数和SGP4/SDP4模型，发展了基于历史轨道数据的神经网络最优阻力系数外推方法，并对国际空间站等大型航天器的轨道衰降进行预测。汤靖师等［5］提出把阻力系数、迎风面积、固定高度密度的组合参数作为外推变量，以开展短弧段和长弧段的轨道预报。从研究现状看，现有的研究以历史轨道数据为基础，往往通过数学手段对阻力系数或者某种组合参数进行外推，从而开展预报，物理意义不明晰。

从空气动力学的角度看，若航天器飞行姿态确定，则空气动力系数可以准确计算得到，并随高度呈现出可用空气动力学解释的变化规律。基于这点考虑，并结合传统的基于历史数据的轨道外推预报策略，本文提出无控航天器轨道衰降遵循等效迎角的概念和与之相适应的空气动力快速计算建模方法，把稀薄气体动力学融合进航天器飞行轨道衰降数值预报，在失效航天器轨道预报的众多不确定因素中增加可计算建模确定性，提高轨道预报的有效性和精度。

2 轨道动力学计算模型与数值方法

在J2000.0坐标系Oxyz内航天器的运动方程为式（1）。

式中，r是航天器的位置矢量；F是航天器所受合外力引起质心运动的加速度矢量；t是飞行时间。

对于低轨航天器，上述轨道方程组中的外力主要是地球引力、空气动力和日月引力。本文用地球引力位函数计算地球引力，其中略去田谐项，考虑至四阶的带谐项系数J2、J3、J4。地球的引力位函数可写为式（2）。

式中，U是地球引力位，φ是地心纬度，r是飞行器质心到地球质心的距离，Re是参考椭球体赤道半径。引力加速度G可通过对引力位求梯度得到，如式（3）所示。

在日、月引力模型中，将太阳、月球视作质点，根据非惯性坐标系中的受力分析，给出日、月引力模型［2］，其中太阳、月球位置由NASA的JPL DE405星历计算得到。引力加速度计算公式可写为式（4）。

式中，GS，L为飞行器受到的日（月）的引力加速度矢量；ΔS，L为惯性系中由太阳（月球）位置指向飞行器位置的矢量，ΔS，L是其大小；μ为太阳（月球）引力常数，μS=1.327 124 38×1020m3/s2，μL=1.327 124 38×1012m3/s2。下标S代表太阳，L代表月球。

空气动力项模拟的准确性，直接决定轨道动力学方程求解的可靠性，其中大气密度采用MSIS00模型计算［4］，空气动力系数需要根据航天器当前飞行高度、速度与空间飞行姿态建模确定，详见第3节。

文献［2］讨论了航天器运动方程的选择及求解方法，认为对于方程式（1）中以r和·r为自变量的运动方程，右函数形式简单但变化快，时间步长较小。基于此，并考虑到减小数值误差的需求，本文以较小的时间步长（0.01 s），利用十阶Adams预测-校正格式对轨道方程组进行数值积分。

3 无控航天器轨道衰降模拟的等效迎角与空气动力系数一体化计算建模方法

3.1 基于空气动力精细数值模拟驱动的低轨航天器气动力特性快速算法

为了获得航天器轨道衰降与再入全过程准确的气动力特性并满足沿轨道生产海量数据的工程需要，李志辉等［12-14］建立了由跨流域空气动力学精细模拟方法驱动的当地化快速计算工具，并计算分析了大型航天器的气动力特性［12］。

高超声速空气动力特性当地化快速算法是一种基于自由分子流与连续流的当地化桥函数理论关联方法，基本思想是［7，12-13，15］：当地面元上的气动力系数只依赖于来流和当地性质，如当地迎角、当地表面作用等；在连续流和自由分子流区域，气动力特性遵从不同的物理定律，当地面元上的气动力系数分别用连续流和自由分子流的方法计算；对于连续流和自由分子流之间的稀薄过渡流区，当地的气动力系数用桥函数进行关联适应。当地气动力系数又可细分为当地压力系数和摩擦力系数。

针对航天器轨道衰降过程空气动力特性当地化快速计算，本文具体采用的方法［12］为：在连续流区域，采用修正牛顿流理论、二次激波膨胀方法以及背风真空效应法估算当地气动力系数［16］；对自由分子流区域，使用基于不同模型材料修正的Nocilla壁面反射模型进行压力与摩擦力系数计算［17］；在稀薄过渡流区域，采用修正的Boettcher/Legge非对称桥函数理论［15］，建立了可分段描述的非对称压力与摩擦力系数关联桥函数，以对连续流区和自由分子流区的气动力系数进行关联，其中包含3个压力系数关联参数Knn，p、ΔKnp1、ΔKnp2以及3个摩擦力系数关联参数Knn，τ、ΔKnτ1、ΔKnτ2。基于这些关联参数，稀薄过渡流区域的非对称压力桥函数Fb，p1和Fb，p2可写为式（5）。

稀薄过渡流区域的摩擦力桥函数Fb，τ1和Fb，τ2可写为式（6）。

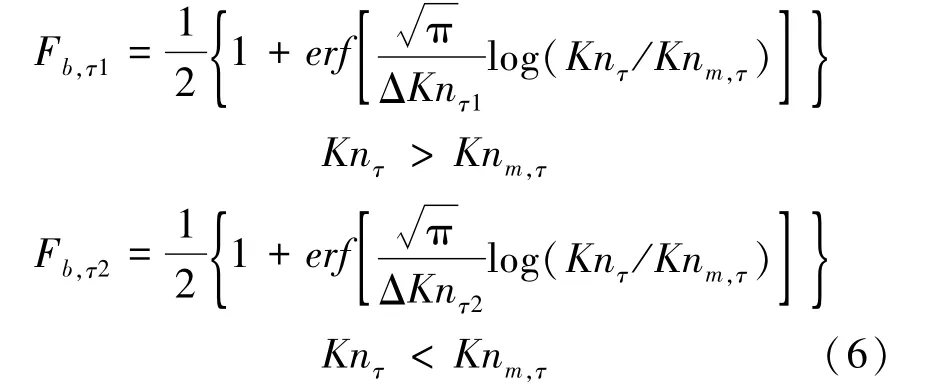
式（5）～（6）中，Kn0，∞是飞行器克努森数，。

本文首先依靠DSMC方法和求解Boltzmann模型方程气体动理论统一算法（GKUA）等跨流域气动力精细模拟手段，对高度250～110 km的流场和气动力系数进行精细模拟。然后基于气动力系数精细模拟结果，调试选择与计算修正这6个关联参数，使当地化快速预测结果最大程度地符合精细数值模拟结果。

图1给出利用前述的低轨航天器气动特性一体化快速算法得到的无控陨落大型航天器B在高度350～100 km的气动力特性。航天器B的外形包含了中间主体功能舱、两侧的太阳能电池帆板以及其他小部件（图1（a）），气动力参考面积取中间主体功能舱横截面积。由图1（b）中阻力和升力系数随迎角变化曲线可见，阻力系数和升力系数随迎角在0～180°范围变化较大，阻力系数在0°和180°迎角下最小，在90°迎角下最大；升力系数随迎角在0～180°范围呈现反对称正弦分布，且分别在8°和98°迎角改变符号。图1（b）还比较了当地化快速算法（图中标注为Local）得到的气动力特性与DSMC数值模拟结果，可以看到两者的变化规律吻合较好。由于DSMC方法是稀薄过渡流区域流场和气动特性最可靠的计算方法，本文通过与DSMC结果比较，验证了当地化快速算法的有效性和精度。由图1（c）可见，阻力系数随高度变化明显，整体上随高度的减小而减小，在高度180 km以上随高度的减小而缓慢下降，而在高度180 km往下剧烈变化。

图1 大型航天器B在高度350～100 km的气动力特性Fig.1 Aerodynam ic characteristics of large spacecraft B at 350～100 km altitude

3.2 无控航天器轨道衰降模拟的等效迎角法

在航天器受到良好控制、姿态稳定的情况下，可采用3.1节所述的空气动力学建模算法获得气动力特性并进行轨道衰降数值预报。然而很多失效航天器通常处于无控飞行状态，不仅存在随质心的三自由度轨道运动，还存在绕质心的自旋转动。自旋航天器飞行姿态上的不确定性会严重影响空气动力特性预测结果，进而影响轨道预报的精度。导致航天器自旋的因素众多，现有的观测手段很难准确甄别，且作为精确预测手段考虑转动角速度的六自由度轨道与姿态动力学计算建模有待深化研究。观测表明，作为本文研究对象的大型航天器B，因突发故障功能失效，处于无控飞行状态后，其飞行姿态逐渐失稳，处于绕质心自旋状态。研究分析同样表明，欧空局ESA的对地观测卫星ENVISAT在2012年4月失效后，在缓慢衰降的轨道上以1.5～3°/s的角速度自旋［18］。

从3.1节的计算分析可见，由于航天器B的升力随姿态角的变化而改变符号，总体上正升力的迎角区间长度与负升力的迎角区间长度相等。因此当航天器自旋转动一周后，升力对轨道的影响基本抵消。图1（b）还可看出，升力与阻力相比是小量，升阻比小于0.05，从量值上说明升力的影响小。航天器所受大气阻力，根据空气动力学理论表达为式（7）。

其中，Cd是阻力系数，S是参考面积，V是航天器相对于大气的飞行速度，ρ是大气密度。轨道动力学领域和空气动力学领域对参考面积S的定义和计算方法不同。轨道动力学通常认为［2］，S是垂直于速度V方向的迎风面积，随飞行姿态变化；而空气动力学通常把参考面积S取为飞行器不随姿态变化的特征面积［3］，如底部面积、翼面面积、横截面积等。引言部分已经分析了当前低轨航天器轨道衰降预报的国内外现状。从空气动力学角度分析，当前的研究没有充分利用稀薄气体动力学的研究成果，或者反演参数数量多，或者用于预报的数学外推缺乏物理意义。

本文基于空气动力学专业角度，把式（7）中的参考面积S作为固定不变的无量纲参考量，提出另一种方案，即结合前述的空气动力特性当地化快速算法与轨道计算模型，拟合确定航天器的姿态角，即等效迎角。等效迎角不是航天器实际飞行的姿态角，而是一种阻力姿态角，飞行器阻力系数的计算依赖于等效迎角、飞行速度和飞行高度。当采用等效迎角预报时，阻力系数随飞行高度的变化可根据稀薄气体动力学获得的气动力特性自动获取，具有实际的物理意义。利用等效迎角预报无控航天器飞行轨道的步骤为：

1）对于某航天器外形，通过3.1节所述由空气动力学精细模拟方法驱动的气动力当地化快速算法，得到以速度、高度和迎角为自变量的气动阻力系数数据表。

2）利用某一弧段的外测轨道星历数据，拟合得到等效迎角。

3）把历史弧段的等效迎角直接作为预报弧段的等效迎角；或通过连续几个历史弧段的等效迎角，优化拟合得到预报弧段的等效迎角。

4）基于预报弧段的等效迎角计算获取航天器气动力特性与飞行航迹，开展轨道预报。

等效迎角的拟合确定，作为初步研究，设计了如下迭代过程：

1）估算等效迎角 αd的范围： α1≤αd≤α2，在此范围内取n个离散点 αi（i=1，2，…，n）。

2）选择外测轨道星历数据中n个点的位置数据ro，j( j=1，2，…，n)作为比较数据。

3）选择该历史弧段的起点作为轨道计算初始点，对于每个迎角的离散值αi，都进行一次轨道计算，计算相同时刻模拟的轨道与n个要比较的历史位置数据距离的平均值Ed，i，如式（8）所示。

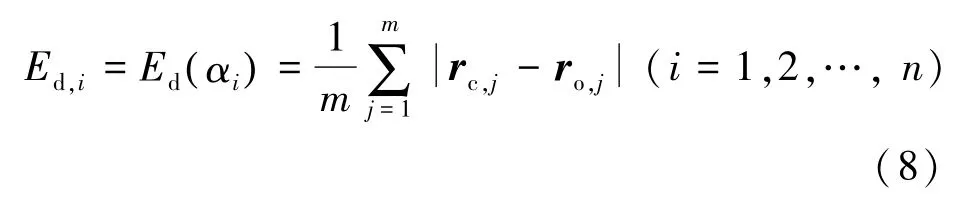
式中，rc，j是与比较数据ro，j在相同时刻的模拟数据。为了加快计算速度，可在计算集群上采用并行计算技术，用n个计算核心分别计算n条轨道。

4）获得（αi，Ed，i）序列后，则等效迎角 αd为Ed最小值对应的迎角，即式（9）。

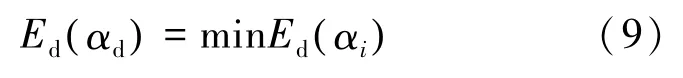
4 计算结果及分析

以大型航天器A受控再入和大型航天器B无控飞行轨道衰降为研究对象，开展计算分析，航天器B的外形如图1（a）所示，航天器A的外形与之相似。大型航天器A受控再入大气层，在最后一次变轨制动后以固定姿态稳定飞行，迎角保持不变，星上GPS装置测量到轨道衰降过程中的位置数据。大型航天器B失控后，姿态失稳并处于自旋状态，通过地面雷达等设备得到轨道衰降过程中的位置数据。

4.1 大型航天器A受控陨落轨道衰降计算分析

大型航天器A受控陨落姿态稳定不变。本文依据轨道衰降过程中固定的飞行姿态，通过3.1节所述由空气动力学精细模拟方法驱动的低轨航天器跨流域气动力特性一体化快速算法得到阻力系数，使用3.2节所述的直接积分高精度轨道计算方法进行轨道计算。大型航天器A最后一次变轨后，以固定迎角飞行220～100 km过程的飞行航迹计算结果如图2所示。由图可见，在大型航天器A飞行高度从220 km下降到100 km的过程中，计算得到的空间位置（地固坐标系）结果与GPS实测数据吻合较好。详细比较表明，计算的位置结果和GPS数据偏差不超过10 m。这说明本文发展的轨道计算以及低轨航天器气动力特性计算模型及方法具有较好的可靠性与精度。

4.2 大型航天器B无控陨落轨道衰降计算分析

4.2.1 长弧段预报

利用3.2节介绍的无控航天器轨道衰降等效迎角方法，对大型航天器B无控飞行350～300 km轨道衰降过程进行分析。图3（a）给出经过式（8）计算获得的 （αi，Ed，i）序列曲线，即计算位置平均误差随迎角变化曲线，其中所选择的历史观测数据弧长为1个月。根据式（9），图3（a）曲线最低点所在的迎角就是此弧段拟合确定的等效迎角，量值为42°。预报弧段位于等效迎角拟合弧段之后1个月。把42°等效迎角作为预报弧段的等效迎角，开展预报弧段的轨道预报，得到预报弧段同一时刻预报位置相对测量位置的误差δr，如图3（b）所示。可看出，预报的空间位置误差随预报时间的增大而增大，预报5天的位置误差约为42 km，预报10天的位置误差约为316 km，预报30天的位置误差约为1137 km。利用轨道速度估算，预报30天的位置误差相当于在时间上偏差约150 s，占轨道周期约2.8%。这说明了本文发展的等效迎角气动融合轨道直接积分高精度计算模型，可以得到较好的长弧段预报结果。

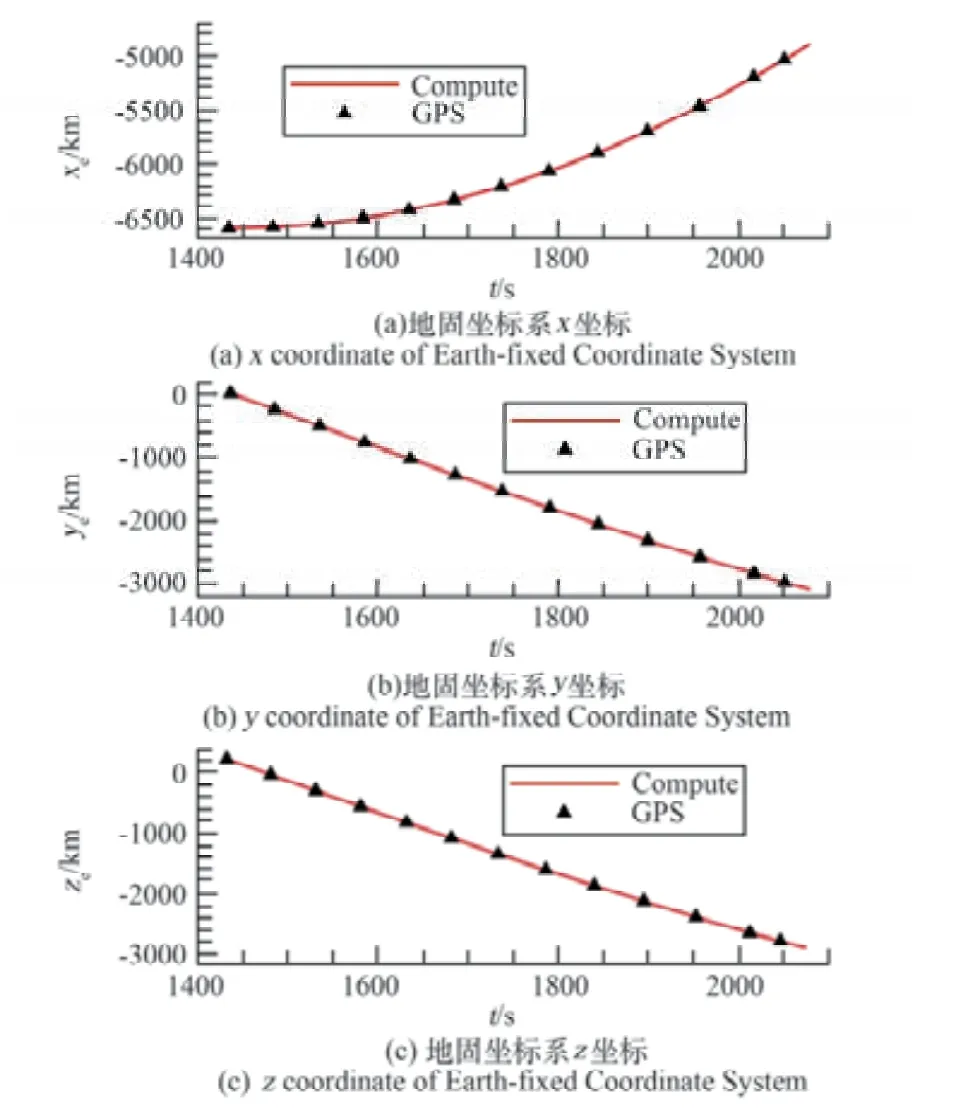
图2 大型航天器A受控陨落220～100 km高度空间位置计算与GPS测量数据比较Fig.2 Comparison of orbit position between computation and GPS measurement for controlled reentry spacecraft A at 220～100 km altitude

图3 大型航天器B无控飞行轨道衰降长弧段预报结果（预报弧段为1个月，等效迎角拟合弧段为预报弧段的前1月，轨道高度350～300 km）Fig.3 Com putational results of orbit decay for large spacecraft B（The prediction arc is onemonth and the inversion arc is onemouth before prediction arc.Orbit altitude is 350～300 km）

等效迎角反映了失稳自旋航天器在拟合弧段的平均阻力姿态角大小。当直接应用到预报弧段时，隐含的假设是预报弧段的航天器无控飞行姿态与拟合弧段的飞行姿态具有继承连续性，彼此相差不大。图3中轨道高度范围（350～300 km）变化不大，外界扰动因素有可能没有发生明显变化，使得此时的无控航天器自旋运动模式和飞行姿态没有发生明显改变。

4.2.2 短弧段预报

当利用等效迎角气动融合轨道直接积分建模方法开展短弧段预报时，拟合弧段需要保证较合适的长度，以反映等效迎角的变化。利用大型航天器B再入前5天的外测轨道星历数据与3.2节介绍的方法，得到等效迎角的变化规律，如图4所示，其中拟合弧长为1天。可看出，再入前5天等效迎角变化较大，从再入前倒数第5天的32.3°减小到再入当天的20.9°。

图4 大型航天器B无控陨落再入大气层前5日根据每日观测数据得到的等效迎角Fig.4 Equivalent-angle-of-attacks of large spacecraft B obtained from dailymeasured data during 5 days before uncontrolled re-entry

图5给出再入前倒数第3天轨道位置预报偏差，预报中采用的等效迎角通过再入前倒数第4天外测轨道星历观测数据拟合得到。可看出，预报误差随着预报时间的增大而增大，预报5 h轨道位置误差为1.3 km，预报24 h轨道位置误差为19.6 km。利用轨道速度估算，预报24 h的时间偏差约为2.6 s。这说明本文等效迎角气动融合轨道直接积分模型方法可以得到准确性高的短弧段预报结果。

图5 大型航天器B无控再入大气层前倒数第3天轨道预报结果误差（按倒数第4天外测轨道数据拟合等效迎角计算）Fig.5 Prediction error of orbit position on the 3rd day before uncotrolled re-entry of large spacecraft B（calculated by the fitted equivalent-angle-of-attack from measured orbit data on the 4th day before re-entry）

5 结论

1）对大型航天器A受控陨落220～100 km过程飞行航迹的计算分析，验证了本文由空气动力精细数值模拟驱动的低轨航天器气动特性快速算法以及轨道动力学预报模型及方法的有效性。

2）在大型航天器B无控失稳自旋飞行轨道衰降计算分析中，得到了与外测轨道星历数据吻合一致的长弧段和短弧段预报结果，在停止外测轨道数据供给5 h内，地心惯性系位置预报偏差低于1.5 km，验证了基于等效迎角的气动融合轨道直接积分计算模型对无控航天器轨道衰降预报的合理性。

3）所建立基于等效迎角的气动融合轨道数值预报模型，是一种初步的方法。下一步可结合空气动力学中的气动参数辨识理论以及轨道动力学中的反演方法，对等效迎角进行更准确合理的拟合优化确定，为大型航天器再入解体分析提供更准确的再入点数据。