连锁便利店会员最优折扣模型研究

嵩 涛，欧齐备，刘 维

(贵州烟草投资管理有限公司，贵州 贵阳 550003)

1 概述

电商早期借助互联网红利获得了飞速的发展，随着互联网的流量红利期逐步消失，该模式的发展已经遇到瓶颈。为能够获取客户流量，零售电商回归本质，通过发展线下连锁零售店，线上流量与线下体验相融合寻找新的增量，利用线上积累的消费数据和技术去赋能实体零售[1-2]。因此，连锁便利店作为新零售线下发展的重要载体在近几年得到快速发展。连锁便利店企业为吸引消费者，常通过会员制采用各种促销手段提高顾客忠诚度，其中针对会员的商品折扣促销最为常见。那么，连锁便利店如何制订最优折扣率，在同时存在积分抵现的情形下，折扣率又该如何制订，这些都是本文要研究的内容。

会员积分制是典型的非价格策略，已有研究表明积分能够对消费者的购买行为产生显著影响[3-4]，而会员折扣实际是价格策略，其实际效果已经被众多研究所证实[5-6]。在新零售背景下，连锁便利店常采用折扣且积分的形式进行促销，即采用价格与非价格策略结合的方式。基于此，本文拟从价格策略、价格策略与积分抵现结合两个角度分别建立最优折扣模型，并以黔彩便利店酒类快消品为例对模型进行验证，以期为连锁便利店会员管理提供参考。

2 统一折扣模型

黔彩连锁便利店商品成本加成定价法，设某商品进价为c，加成比例为β，无折扣情形下其需求量为d，此时该商品总利润为[(1+β)c-c]d=βcd。

便利常通过对会员打折促销的方式增加商品销量，即薄利多销的方式增加收入。假设其商品折扣率为α，且0≤α≤1此时销量增加为λd(1-α)，其中正常数为折扣因子。在不考虑其他促销成本、人力成本的情形下，不考虑积分成本时，此时商品总利润为：

maxxπ(α)=[α(1+β)c-c][λd(1-α)+d]

(1)

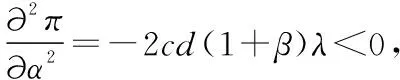
3 统一折扣与积分模型

会员购买商品的同时获得相应的积分，通常每元积分为1分，会员再通过积分兑换抵扣现金。设抵扣率为f，即每积分可抵扣现金f元，且f<1。由于抵扣率一般而言非常低，对需求量影响在本文中忽略不计。由此，得到商品的利润为：

maxxπ(α)=[α(1+β)c-c][λd(1-α)+d]-
[α(1+β)c][λd(1-α)+d]f

(2)

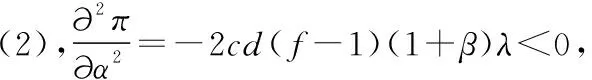
4 模型仿真

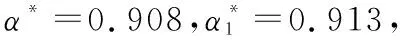
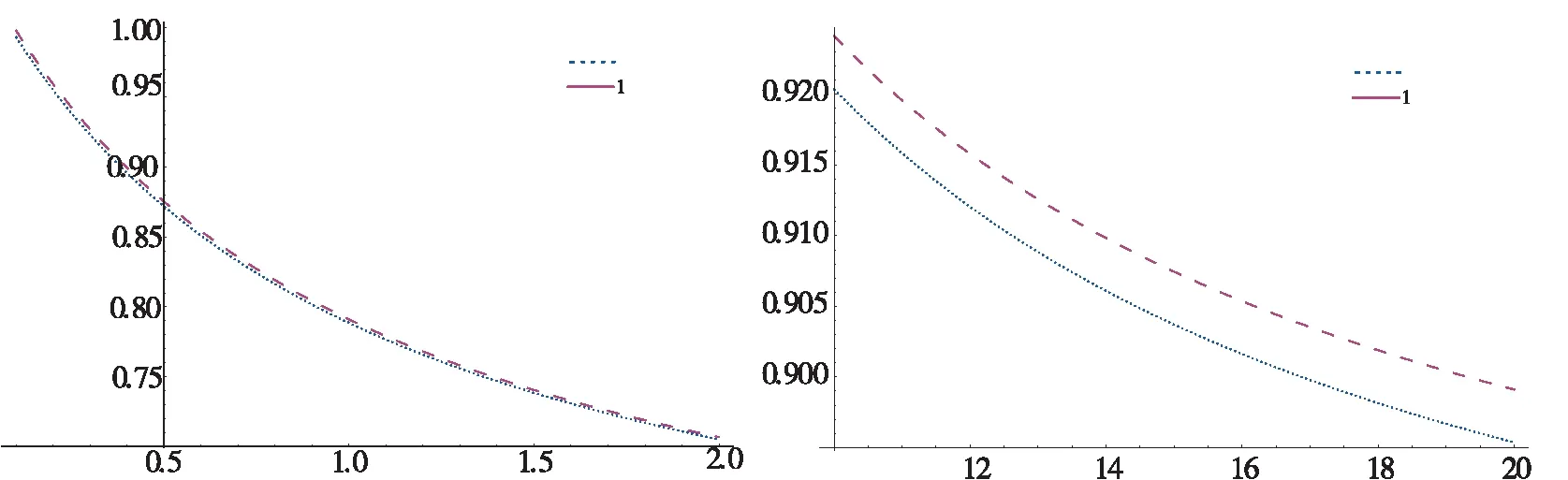
图1 最优折扣随β变化情况 图2 最优折扣随λ变化情况

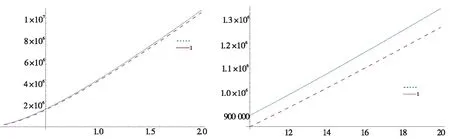
图3 最优利润随β变化情况 图4 最优利润随λ变化情况

从图1-图4中可以看出，无积分时的折扣率总是低于有积分时的折扣率，表明无积分时的折扣力度较大。随着加成定价、折扣因子的增加，折扣率降低，表明折扣力度也需要增加。从利润来看，无积分时的利润总是高于有积分时的折利润，且随着加成定价、折扣因子的增加利润也逐步增加。

5 结语

本文运用最优化理论，根据加成定价法建立了连锁便利店会员最优折扣模型，并以黔彩连锁便利店酒类快消品为例对模型进行了验证，给出了一定条件下的最优折扣率。结论表明通过会员折扣促销有利于连锁企业利润的增加，但在积分可抵扣现金的情形下最优利润会降低。由于本文只考虑到一种商品，也未考虑积分对需求的影响这可能是导致积分抵扣时出现利润下降的原因，但在实际应用中，一种商品的积分促销可能会带动其他商品需求量的上升，从而从总体上增加利润，这一问题的理论研究是下一步的研究方向。