技术站间货物列车协同配流方案研究

武 旭，杨义静

(北京交通大学交通运输学院，北京100044)

0 引 言

技术站配流问题是铁路运输生产的核心工作之一，将两个技术站看作一个整体，对其作业过程进行协同优化，必将获得更大的运输收益.在铁路市场化转型，提升铁路货物运输生产效率的背景下，研究技术站间货物列车协同配流问题具有一定的理论和现实意义.

长期以来，技术站配流问题多以单技术站进行研究.单技术站配流作业在于确定列车解编顺序及出发列车的车流来源.许多学者从优化列车解编顺序、动态配流等多方面进行研究.Yaghini等[1]通过构建混合整数规划模型优化列车解编顺序，Kraft 等[2]通过构建列车解编顺序优化模型，研究车流分配问题.呼志刚等[3]通过调整铁路编组站列车解编顺序优化配流.上述文献虽对配流方案进行优化，但其均将解体作业时间取定值，而在实际作业中，解体技术作业时间与列车编组内容有关[4].景云等[5]基于概率利用回归分析估算解体作业时间，分别在动态配流与静态配流的条件下建立配流模型.其列车解体作业时间虽接近实际情况，但列车出发条件并未考虑列车换重、换长因素的影响.

本文在考虑列车解体作业时间、列车满足换重、换长及车辆数的出发条件前提下，根据列车运行前方技术站列车出发情况，调整后方技术站列车配流作业，获得两技术站整体效益最高的配流方案.论文首先完成基于两技术站的协同配流模型的构建；其次，设计完成用于求解所建模型的启发式遗传算法；最后，通过算例验证技术站间协同作业的有利性.

1 问题描述与模型构建

1.1 问题描述

随着全路高铁、普速新线建设，既有线客货分线初见成效，线路通过能力有了较大释放，路网节点能力成为制约货物运输质量的突出因素.此外，铁路网上各技术站间作业相互关联，技术站内车流作业不仅关系到本站工作效率和效益，也对其他技术站产生影响.因此，为提高铁路网利用效率和货物运输效益，有必要考虑技术站间协同作业.

本文以图1中技术站位置为例展开研究，列车运行方向定为箭头所指方向.

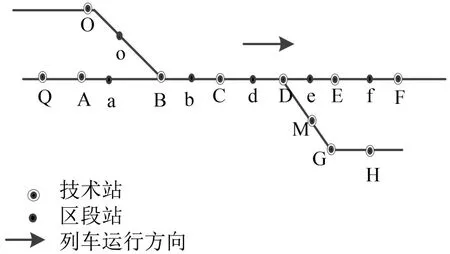
图1 技术站位置示意图Fig.1 Schematic of technical stations

以图中技术站B、C为研究对象，在阶段计划时间内组织技术站C 配流作业，其会受到上一阶段结余车流以及后方技术站B 发出到C站同方向列车的影响.同时，由于B站为C站提供车流，为使该部分车流能够较早到达C站，需调整B站开往C站的货物列车解编顺序.因此，B站的作业情况也将受到C站的影响.本文研究技术站B、C间的协同配流作业，根据C站某方向列车集结及出发情况，调整B站列车配流内容及解编顺序，使两技术站正点出发列车数最多.

在技术站间列车配流问题中，由于列车出发时间已定，若其能正点出发，则阶段内车辆在站停留时间最少[6]，因此本文以正点出发列车数最多作为评判配流方案优劣的标准.以C站开往H及其以远的车流为例，由于欠轴无法正点发车：B站阶段计划中含有由B站开往C站和H 及其以远的出发列车.此时，考虑技术站间协同配流作业.在货物列车配流作业过程中，调度人员根据C站的日班计划可预知站内车流到达情况，由此可知C站发往H及其以远方向的出发列车是否能够正点出发.若不能，则考虑相邻两站之间的距离及技术作业时间，判断B站与C站协同作业的时间阶段.若此阶段内B站到达列车含有编组去向为H 及其以远的车流，则改变到达列车的作业顺序，将该车流合并到B至C的列车，为C站H 方向列车补轴，保证C站列车正点发车.技术站B在为技术站C提供车流的同时，也会使技术站B的车流在站停留时间减少，使得两技术站配流结果都能得到优化.

1.2 模型构建

本文以技术站B为例，考虑C站车流需求对B站作业的影响，构建协同配流模型.

(1)解体技术作业时间.

本文借鉴文献[5]中考虑摘挂钩数的作业时间计算方法，TB=ax1+bx2+c，其中，TB表示到达列车解体作业时间，x1与x2分别表示非禁溜车组与禁溜车组的解体钩数，a、b为回归系数，c为随机误差项，均可根据站内历史数据分析得到，视为已知参数.

(2)假设条件.

为了简化车流组织作业的复杂度，本文将一些不确定因素转化为确定因素.提出以下假设：

①阶段计划内列车正点到达，出发列车均满足满轴条件；

②调车组织作业采用单推单溜方式；

③技术站线路能力充足，可实现站内连续接、发车.

(3)符号说明.

车流变量，用来表示到达、出发车流信息.阶段计划内到达货物列车为m列，出发货物列车为n列，列车组号最大为K.到达列车解体顺序为S1,S2,…,Sh,…,Sm(列车到达顺序1,2,…,m的随机排列)；出发列车编组顺序为R1,R2,…,Rl,…,Rn(列车出发顺序1,2,…,n的随机排列).Nik表示到达列车i编组内容为组号k的车辆数(i=1,2,…,m；k=1,2,…,K)，kj表示出发列车j所含车组号(j=1,2,…,n；kj=1,2,…,K).xijks为0-1变量，按到达列车同一组号车辆的编组顺序从头到尾依次排序.当到达列车i中组号为k的第s辆车提供给出发列车j时，xijks=1；否则为0.zijk为到达列车i为出发列车j提供组号为k的车辆数.

时间变量，用来记录车流作业相关时间.to为阶段结束时刻，为列车i到达时刻为列车j出发时刻；为到达列车i解体作业时间，TM为出发列车编组作业时间，TA为到达技术作业时间，TD为出发技术作业时间；TT表示车辆在站停留时间；表示列车i到达作业完成时刻，表示列车j出发作业完成时刻与分别表示到达列车i解体作业最早开始时刻、实际开始时刻与结束时刻；与分别表示出发列车j编组作业最晚结束时刻、实际开始时刻与结束时刻.

判断变量，用于判断列车是否满轴出发.Vj、分别表示出发列车j当前车辆数、最小车辆数和最大车辆数；Wj表示当前出发列车j的总重，表示到达列车i中组号为k的第s辆车重量，表示出发列车j最小、最大换重；Lj表示出发列车j当前换长，表示到达列车i中组号为k的第s辆车的换长表示出发列车j最小、最大换长，αj、βj、γj分别表示出发列车是否满足最小车辆数、最小换长、最小换重，满足则取值为1，否则为0.

调整变量，用来表示站内局部调整相关变量.表示B站为C站提供车流列车编组作业最早开始时间与分别表示编组排序为Rl的列车待发时间、编组作业可调整时间、调整后编组作业开始时间与结束时间表示调车机车编组空闲时间；表示提供车流列车编组作业开始时间与出发时间；D表示两相邻技术站间距离，v表示货物列车运行速度提供车流列车到达技术站C的时间.

(4)模型的目标函数为两相邻技术站正点出发列车数最多，即

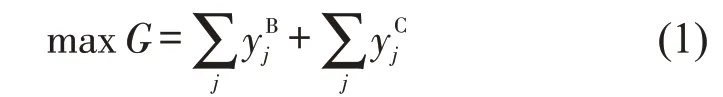
式中：为0-1变量，当B站出发列车j满足正点出发条件时，否则为0；同理，表示C站列车正点出发情况.为了便于描述，在建立约束条件时，将与统称为yj.

(5)约束条件.

到达、解体作业时刻为

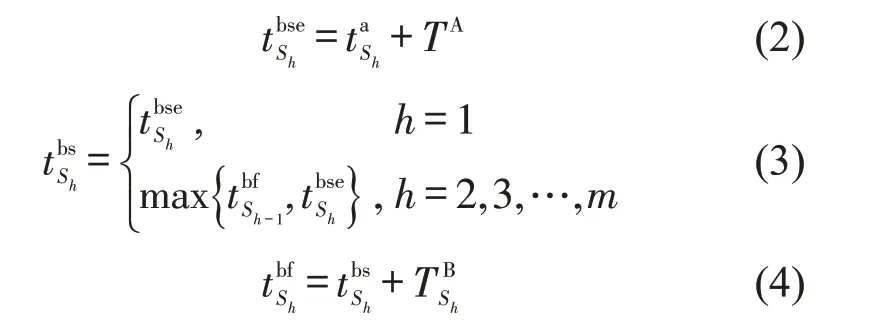
编组、出发时刻为

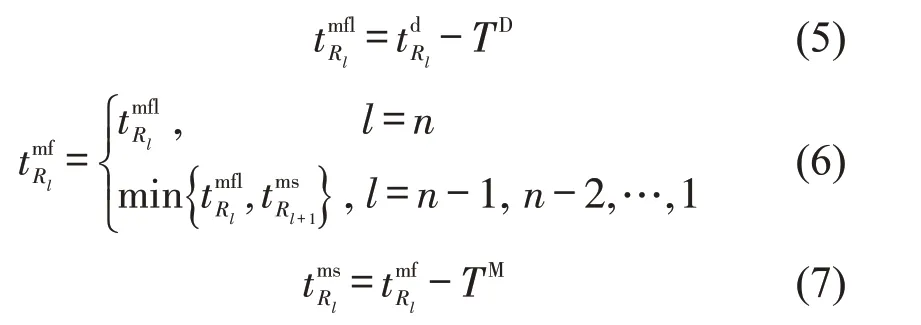
车流接续时刻为

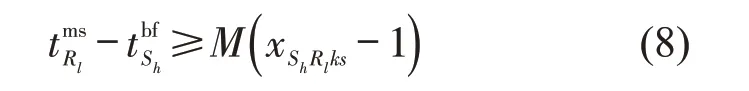
列车出发满轴条件为

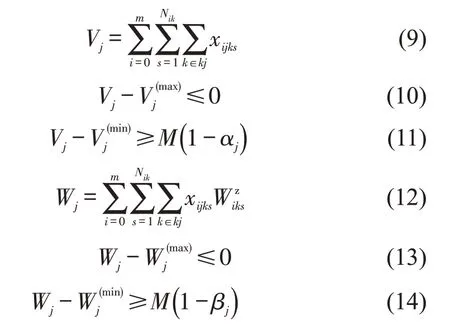
编组内容为

协同配流调整：

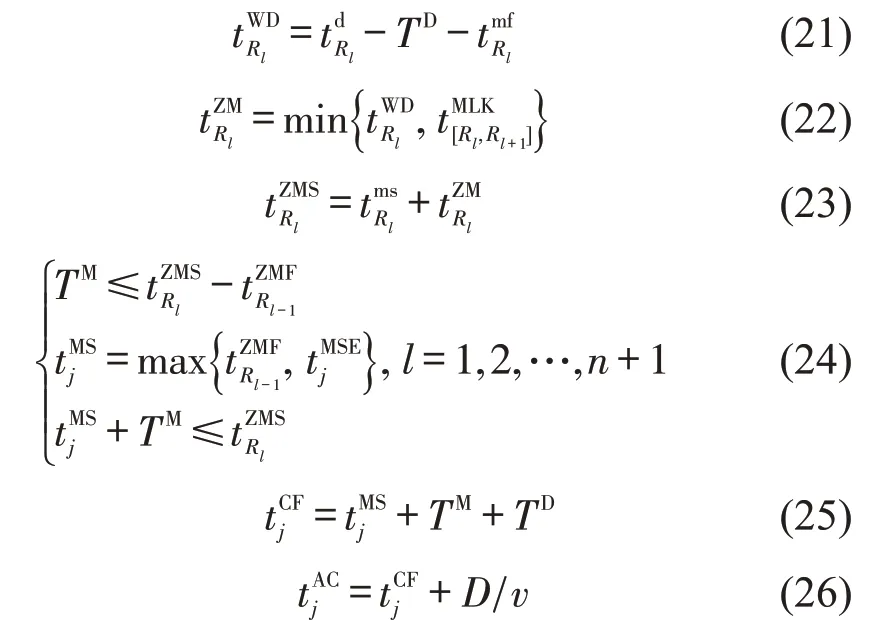
式(2)～式(4)表示到达列车解体作业最早开始时刻、实际开始时刻与实际结束时刻；式(5)表示出发列车编组作业最迟结束时刻；式(6)表示出发列车编组作业实际结束时刻；式(7)表示出发列车编组作业开始时刻；式(8)表示满足车流接续时间要求；式(9)～式(11)分别表示列车j的编成辆数(式(9))，其不得超过最大编成辆数(式(10))，不小于最小编成辆数(式(11))；类似的，式(12)～式(14)则从列车换重角度对列车满轴出发条件进行限制，式(15)～式(17)则从列车换长角度对列车满轴出发条件进行限制.式(18)表示列车只需要满足最小编成辆数、最小换重或最小换长约束式(11)、式(14)、式(17)中的一个；式(19)表示列车j是否正点出发.式(20)表示到达列车i为出发列车j提供的组号为k的车辆数必须小于到达列车i所含有的组号为k的车辆数.式(21)～式(25)表示两技术站协同配流时，技术站B 局部调整约束条件.其中，式(21)表示出发列车待发时间；式(22)表示排序为Rl的列车编组作业开始时间的可调整度；式(23)表示调整后列车编组作业开始时刻；式(24)判断提供车流列车编组作业是否可以插入在编组顺序为Rl-1与Rl之间；式(25)～式(26)表示提供车流列车出发及到达技术站C的时刻.同时设置统计指标用于考察车流在站停留时间，即

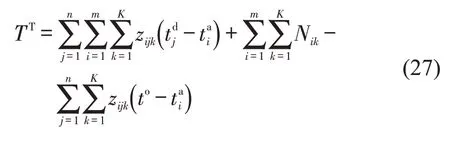
2 流程及算法分析

2.1 流程分析

两技术站间协同作业流程如图2所示.

首先，根据技术站B、C 两站的阶段计划得到各站列车出发情况及结余车流；其次，为保证C站列车正点出发，判断在该阶段B站是否需向C站提供车流.若不提供车流，则直接输出正点出发列车数；否则两技术站进行协同作业；最后，在两技术站单独作业的解编方案基础上进行局部调整.若调整后两技术站车辆在站总停留时间减少，则采用局部调整；否则，将C站所需车流组号添加到B站提供车流列车的编组内容中，并根据C站所需车流的时间条件赋予提供车流列车出发时间，进行全局调整.

2.2 算法分析

货物列车配流作业属于典型的离散型问题，在诸多启发式算法中，遗传算法以生物进化为原型，适用于求解离散问题，具有全局搜索能力，鲁棒性高且优化结果与初始值无关.此外，遗传算法以编码方式优化，具有良好的可操作性，所需辅助信息较少[7]，所以本文采用遗传算法对模型进行求解，主要步骤包括：

(1)通过编码将列车的解编顺序转换为一个遗传基因序列，该序列组成一条长度为m+n的染色体.采用十进制编码方式.染色体前m位编码为1,2,…,m的排列，表示到达列车解体顺序；染色体后n位编码为1,2,…,n的排列，表示出发列车编组顺序.

(2)读取到达列车与出发列车信息，产生初始解，依据出发列车编组开始时间、编组内容以及到达列车解体结束时间，确定出发列车车流接续来源.检验其是否满足列车出发条件，并定义正点出发列车数为算法适应度值，正点出发列车数越大，则适应度值越大.

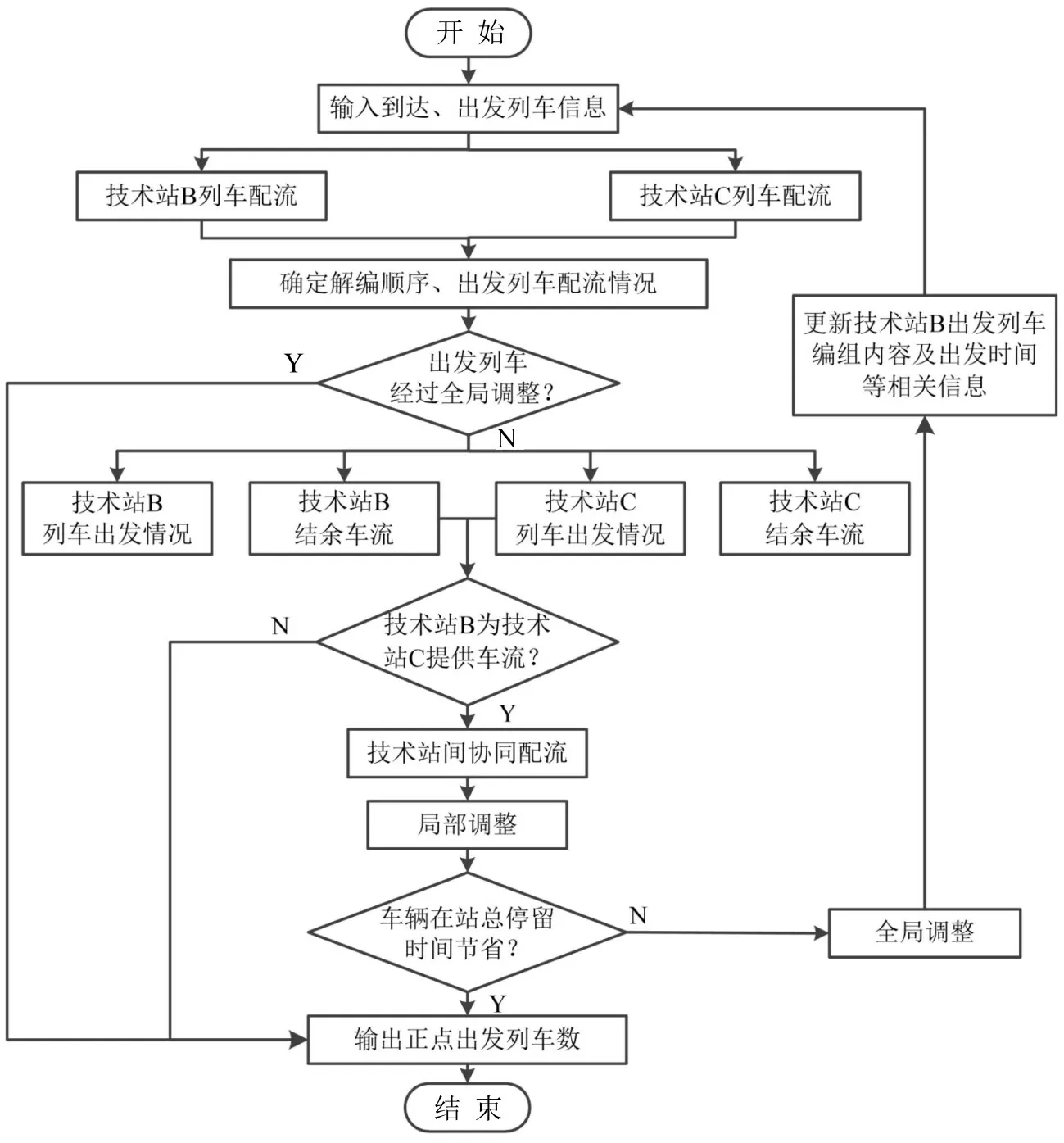
图2 技术站间货物列车配流流程图Fig.2 Flow chart of car-flow organization of freight trains for two adjacent technical stations

(3)以概率Pc选择两条染色体，采用Partial-Mapped Crossover (PMX)算子分别进行染色体前m个基因和后n个基因的交叉操作.

(4)以概率Pm选择变异染色体分别完成前m个基因和后n个基因的基本位变异操作.

(5)终止规则.当算法迭代次数达到终止迭代次数或适应度值达到阶段计划内出发列车数n时，算法终止.

3 算例分析

本节完成算例设计，并用遗传算法进行求解.算法与算例参数具体如下：种群规模为200，终止迭代次数为500，交叉概率Pc为0.80，变异概率Pm为0.05；到达列车、出发列车技检作业时间TA与TD均为30 min，列车编成辆数[50，60]，换长[55，75]，换重[5 000，6 000].列车运行前方技术站为C站，B、C两技术站间距离为280 km，普通货物列车时速80 km/h[8].

通过对基于单技术站列车配流的算法寻优，得到B、C 两站列车解编方案，如表1和表2所示.寻优过程如图3所示.

技术站B、C 协同作业后，两技术站满轴正点出发列车数增加了2列，分别为10016次列车与20024次列车，车辆在站总停留时间节省了77.5 h，两技术站单独作业与协同作业结果对比如表3所示.与技术站单独作业相比，明显提高了站内作业效率.

对比技术站单独配流(表1，表2)和两技术站协同作业结果(表4，表5)，分析发现：

(1)在基于单技术站货物列车配流时，10016次列车的编组去向只有C，不能达到满轴出发条件，而10016次列车欠轴停运增加了车辆在站停留时间.在两技术站协同作业后，10016次列车编组去向为C和H，由于有H 方向车流补轴，达到了列车满轴出发条件.并通过调整B站的列车解编顺序，使10016 能够在阶段时间内发车，为C站配流作业提供需要的车流.与技术站B 单独作业时相比，协同作业后站内车辆在B站总停留时间节省了60 h.

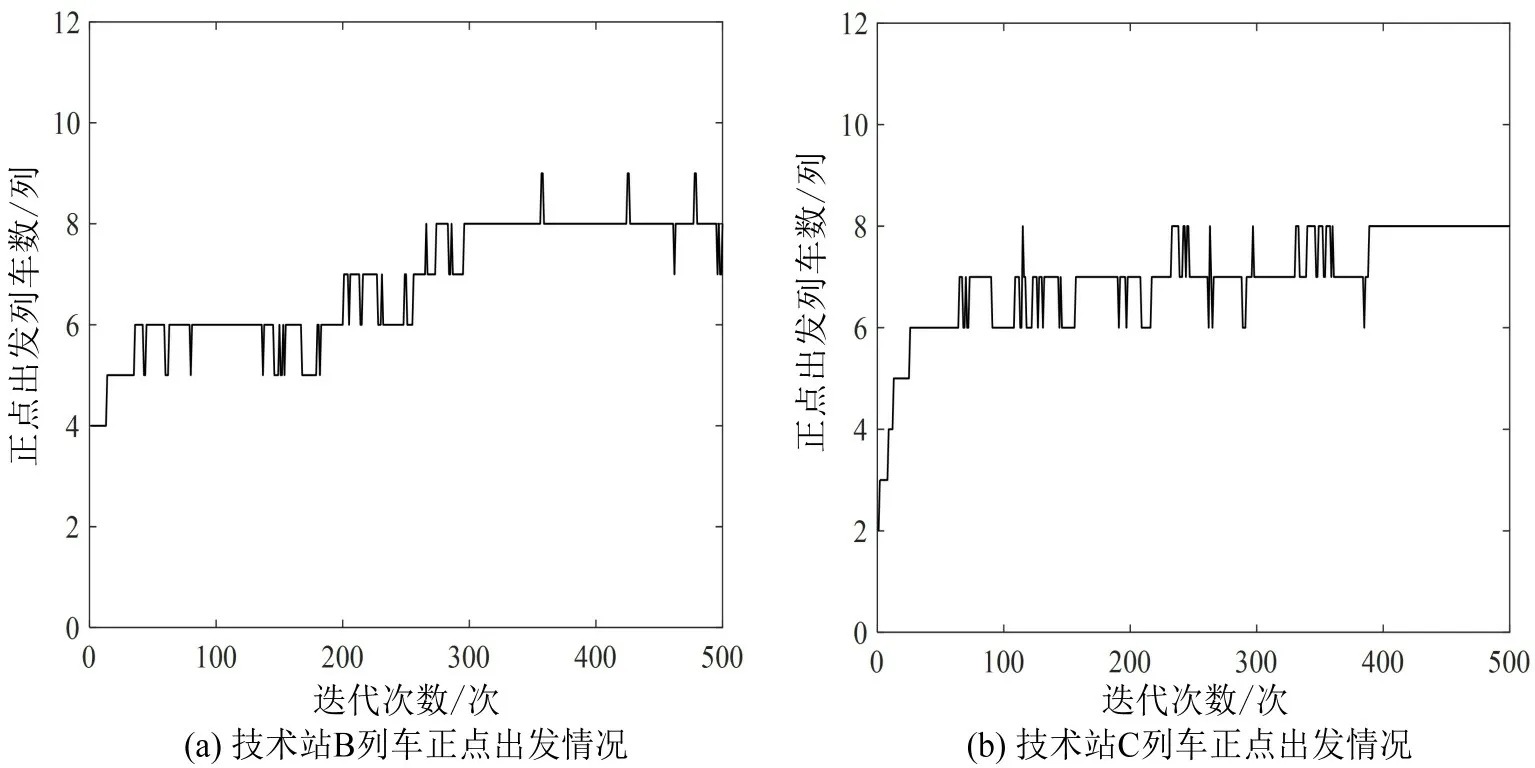
图3 技术站B、C 遗传算法仿真结果图Fig.3 Genetic algorithm simulation results of technical station B and C

(2)技术站单独配流时，C站去往H 方向的20014与20024次列车欠轴停运，而在计算阶段内，B站有H方向结余车流却未提供给C站，使得C站因只进行单独配流而不能减少车辆在站停留时间.两技术站协同作业后，B站的10016次列车为C站提供H方向车流，技术站C中20024次列车达到满轴正点出发条件.技术站C的车辆在站总停留时间比单独作业时节省了17.5 h.

通过以上分析可知，技术站间协同配流模型有助于提高站内线路利用率和货物列车运输效率，可有效避免运行图“丢线”现象.

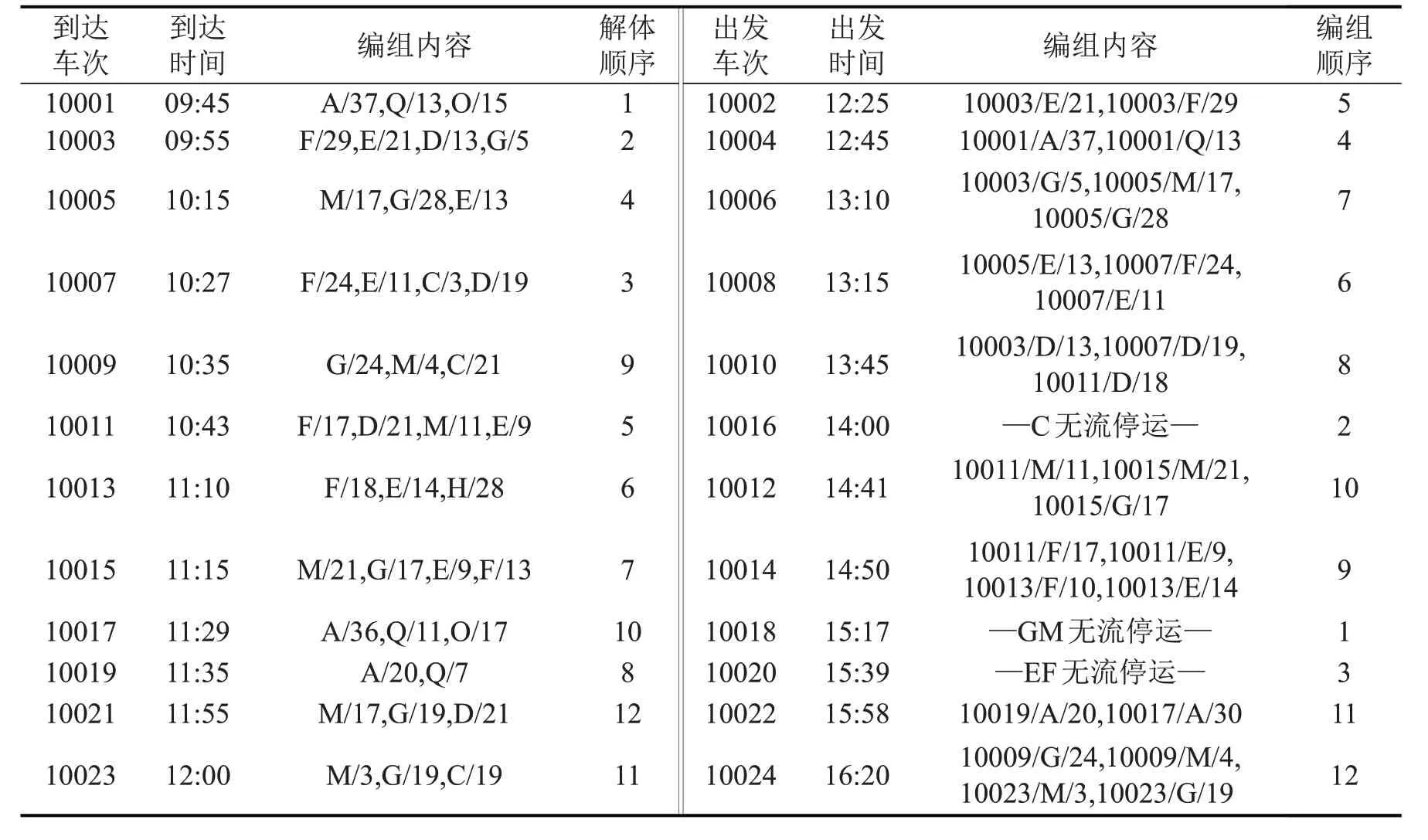
表1 技术站B列车解编方案Table1 Break-up and marshalling plans of trains at technical station B

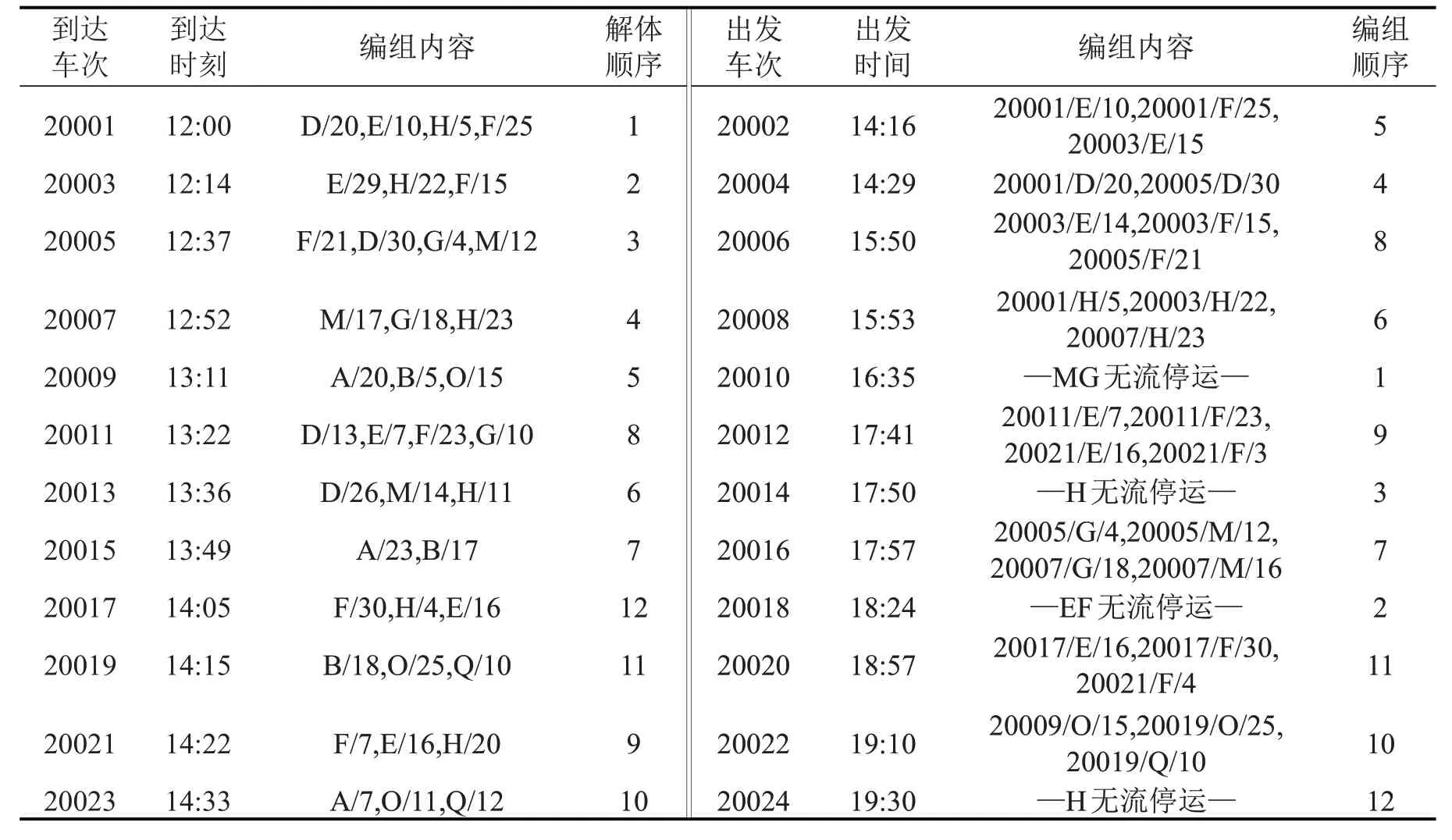
表2 技术站C列车解编方案Table2 Break-up and marshalling plans of trains at technical station C

表3 配流结果对比分析Table3 Analysis of car-flow organization results

表4 协同作业后新增正点出发列车具体信息Table4 Details of newly added trains departing on time after collaborative operations

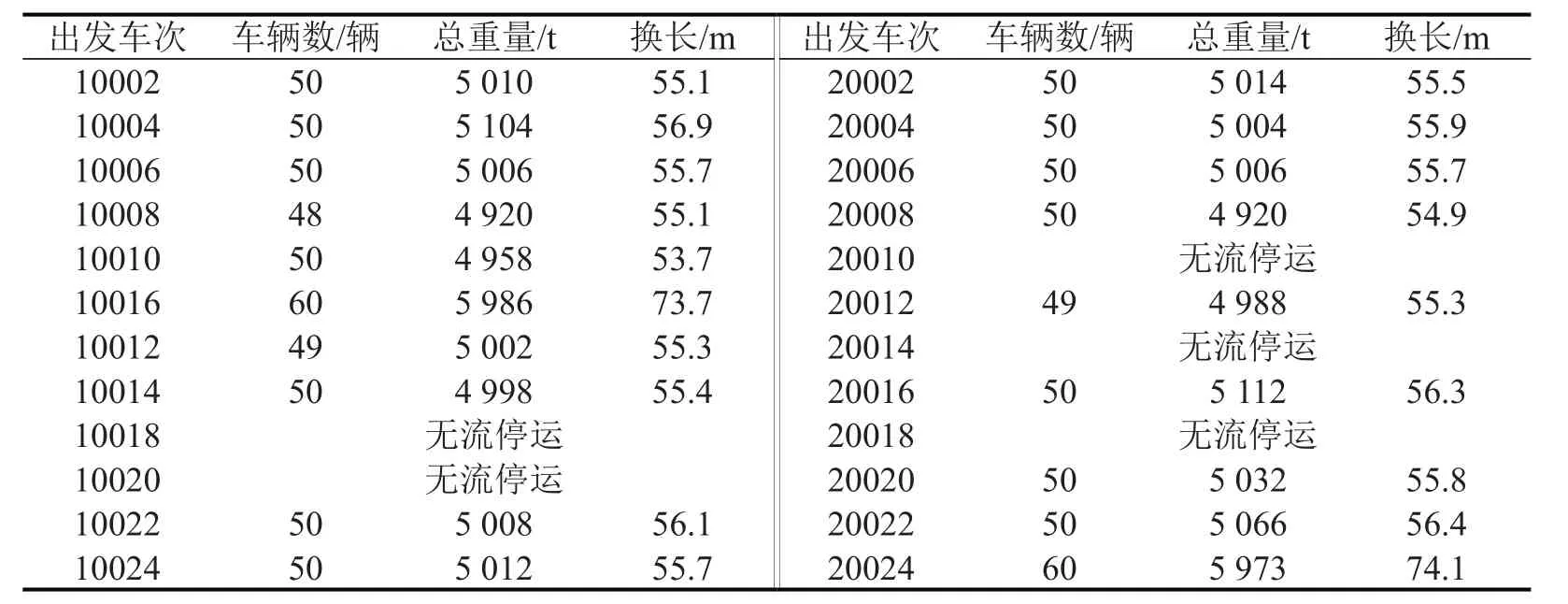
表5 协同作业后两技术站出发列车满载信息Table5 Details of outbound trains after collaborative operation at station B and C

4 结 论

本文在考虑不同满轴约束条件及根据列车实际编组内容估算列车解体作业时间的基础上，构建基于两技术站的列车协同配流模型，并用遗传算法求解模型.通过局部调整和全局调整压缩车辆在站总停留时间，增加两技术站正点出发列车数.最后通过算例证实模型的有利性.相对于单技术站配流作业，技术站间协同配流作业将两技术站正点出发列车数增加2列，车辆在站停留时间节省77.5 h.因此，本研究可有效提高铁路货物运输效率.未来研究中，应从整个铁路网出发，协同优化全路货物列车配流作业.