着陆器足垫与月壤竖向冲击简化动力学模型

钟世英,凌道盛

(1.山东建筑大学 土木工程学院, 山东 济南 250101；2.建筑结构加固改造与地下空间工程教育部重点实验室, 山东 济南 250101；3.浙江大学 岩土工程研究所，浙江 杭州 310058)

2019年1月3日嫦娥四号软着陆成功，标志着我国成为全球第一个实现航天器月球背面软着陆的国家，开启了人类月球探测与应用新篇章[1-2]。2019年4月12日以色列创世纪号撞击月球成为碎片、2019年9月7日印度月船二号着陆失败证明探测器高速降落过程中软着陆难度非常大，着陆缓冲机构的设计是各国深空探测成功的关键[3]。月壤作为着陆器的最终承载者，着陆足垫与月壤在冲击作用下相互作用的有效估算是软着陆成功的重要一环(图1)。

(来源：中国航天科技集团、探月工程)

冲击过程中足垫受力特性是着陆缓冲机构设计的重要依据。国内外学者做了大量工作对月壤特性和冲击动力学问题进行研究。凌道盛等[4]根据软着陆冲击过程的特点设计了竖向冲击模型试验系统，并采用数值模拟方法对冲击过程进行建模分析。马炜[5]针对月壤的散体材料特性，结合多刚体碰撞理论采用离散元方法研究了月壤冲击作用下的动力响应。徐海涛等[6]通过设计探测系统得到了嫦娥四号着陆过程中足垫与月壤冲击过程的影像数据。蒋明镜等[7]采用数值分析法探讨了月壤推剪破坏机制。Sahu等[8]通过振动试验发现砂土阻尼会随着土体结构的改变而变化。Swain等[9]通过土壤流变力学和Prony级数开发新的土动力学时变本构理论，探索更加有效的土体有限元动力分析模型。钱家欢等[10]采用经典结构动力学方法得到了夯击过程中力与位移的关系。王四根等[11]以结构动力学理论为基础采用能量积分法得到了强夯冲击过程中夯击能量吸收率问题的理论解，证明夯击过程中地基加固能量占比与土壤性质有关。

嫦娥三号、嫦娥四号发回的照片表明，月壤表面覆有松散月尘，月壤粗颗粒含量高、颗粒粒径差别大、棱角明显、有空洞。室内试验表明，模拟月壤颗粒在受压过程中破碎现象严重，具有显著的散体材料特性，采用波动法分析冲击过程中足垫所受冲击力时程特性异常困难。为快速、准确地获得冲击过程中足垫与月壤间的相互作用特征，尝试从能量角度建立动力学控制方程，采用精细时程积分和过程参数相结合的方法探索着陆器软着陆冲击荷载的动力响应模型。

1 基本方程

着陆器软着陆冲击过程中，足垫与月壤的相互作用可分为三个阶段[12]：冲击接触、滑移和静止(图2)。为揭示冲击运动机理，得到足垫运动的控制参数，将整个冲击过程简化为竖向冲击(A)和水平滑移(B)两个阶段。竖向冲击段是指足垫与月壤接触开始到月壤反力对加速度影响不大时结束，整个竖向冲击过程加速度改变以月壤反力为主。水平滑移段是指竖向冲击结束后，足垫相对月壤滑移运动，作用力主要来源于足垫与月壤间的动量转化。

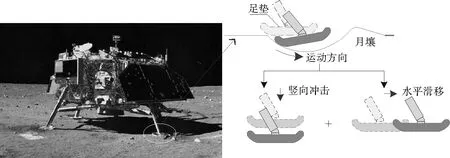
图2 软着陆过程示意图

测试结果表明[4]：竖向冲击过程中足垫接触月壤后，初始几个毫秒内，应力波在月壤内传播深度有限，表层模拟月壤形成加密区[13]。在冲击压缩位移小于临界刺入位移前，月壤呈弹性变形；超过临界刺入位移后，形成塑性破坏区，月壤呈现弹塑性。为研究竖向冲击过程足垫与月壤的相互作用力，建立足垫-月壤竖向冲击物理模型系统(图2)。根据竖向冲击模型试验中轴力和刺入位移曲线测试结果[14]，结合竖向冲击数值模拟中塑性区发展规律[4]，将竖向冲击过程中与足垫作用的月壤划分为两个区域:一个是月壤在足垫冲击作用下形成的塑性区，简称冲剪区；另一个是冲剪区外由冲击作用引起弹性变形的区域称为冲击影响区，简称影响区。

将竖向冲击模型简化为两个自由度的动力系统(图3)，给出竖向冲击过程的动力控制方程。足垫动力平衡方程为：

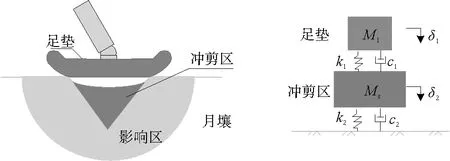
图3 足垫-月壤竖向冲击物理模型系统

(1)

其中：M1为冲击物总质量；K1为足垫与月壤间的有效接触弹簧刚度；c1为足垫与冲剪区阻尼；g为当地重力加速度；r为冲击过程中月壤与足垫接触顶面处足垫半径(0≤r≤rm)；rm为足垫最大半径；δ1为足垫的竖向刺入位移；δ2为滞后月壤的竖向位移。

冲剪区动力平衡方程：

(2)

其中：Ms为冲剪区月壤的质量；K2为冲剪区与影响区月壤的有效弹簧刚度；c2为冲剪区与影响区月壤的阻尼。

2 主要模型参数

室内试验结果表明，月壤强度参数与月壤密实状态密切相关；模型试验结果表明，竖向冲击过程中足垫对月壤具有明显的压密效应[14-15]。结合试验结果，将控制方程中的月壤材料参数与冲击过程月壤状态相关联。

2.1 冲剪区质量

竖向冲击过程中，足垫下月壤塑性区扩展使冲剪区质量不断变化，冲击力传递深度与足垫的直径有关。假定足垫与月壤接触时产生初始楔形冲剪区，则某时刻冲剪区质量Ms(图4)：

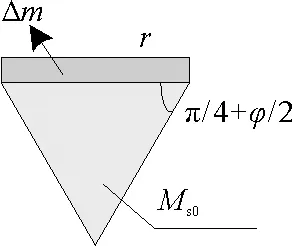
图4 冲剪区质量

Ms=Ms0+Δm。

(3)

由准静力加载下的土锥体理论可得，圆形加载板时产生锥体冲剪区，初始冲剪区Ms0为：

(4)

其中,r为刺入深度处足垫的半径，ρ为模月壤的密度，φ为模拟月壤内摩擦角。

假定时间足够短则冲剪区质量增量可以表示为应变量ε1厚度的小圆柱，则冲剪区质量增量Δm：

Δm=ε1πr2ρ。

(5)

2.2 月壤刚度

假定月壤的弹簧刚度K与应变量相关，月壤弹簧的压缩比率并非定值，与月壤状态相关。半无限弹性连续体受刚性圆盘荷载的弹性系数(弹簧的系数)可表示为：

(6)

其中：Ee为弹性模量，与月壤密实度有关；μ为泊松比；η为弹簧刚度修正系数。与刺入半径r(d)和足垫刺入位移处面积Aft与总的足垫面积Aftm比值：

(7)

其中κ为修正系数，当r(d)=rm时，κ=π。

2.3 月壤阻尼

假定冲击过程中不同状态下的月壤阻尼与月壤材料阻尼比有关，则月壤阻尼：

c=βλ。

(8)

其中：λ为动三轴试验测定的月壤材料阻尼比；β为阻尼修正系数，与月壤密实状态和冲击质量有关。

3 精细时程解

对于竖向冲击问题，需作瞬态历时分析，可采用精细时程积分法进行求解[16]。足垫-冲剪区动力系统控制方程由式(1)、式(2)合记为：

(9)

引入状态向量

(10)

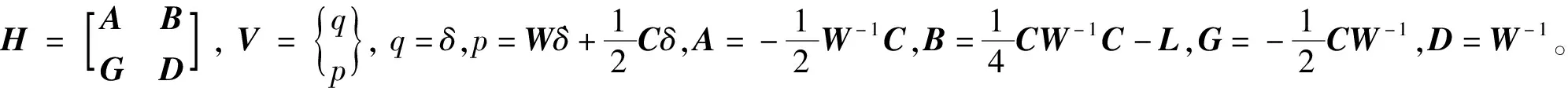
设第k时间步的V值已知，记为Vk,则Vk+1可表示为

Vk+1=T[Vk+H-1(f0+H-1f1)]-H-1(f0+H-1f1+f1Δtk),

(11)

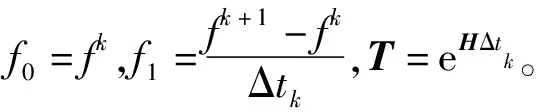
T=eHΔtk=(eHΔtk/m)m,

(12)

取n=2N，Δτk=Δtk/n。若Δτk足够小，则有

(13)

T=[eHΔtk]2N=[I+Ta]2N=[I+Ta]2N-1[I+Ta]2N-1。

(14)

且(I+Ta)×(I+Ta)=I+2Ta+Ta×Ta。

4 计算实例

以模型试验为例(图5)，取足垫直径r=8.3 cm，冲击质量M1=1.5 kg，冲击速度v=1 m/s，月壤密度为ρ=1.202 g/cm3，摩擦角为φ=40°，泊松比μ=0.33，阻尼比为λ1=0.15，λ2=0.12，β1=138.07，β2=57.96，κ=0.284，弹性模量Ee可采用式(15)计算：

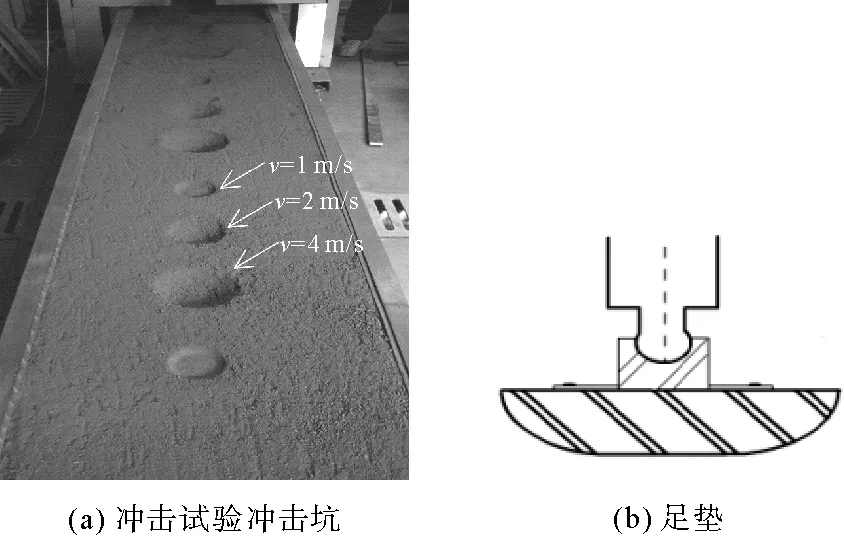
图5 足垫与冲击坑

(15)

图6给出了竖向冲击模型试验测试结果和竖向冲击力学模型计算结果。冲击力时程如图6(a)所示，力学模型能够捕捉到竖向冲击过程中冲击力急速上升至最值，然后快速下降触底反弹的特性，冲击时间基本一致。

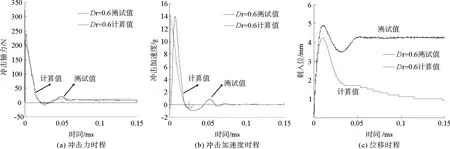
图6 竖向冲击模型试验测试值与计算值关系

冲击加速度时程见曲线6(b)，表明加速度峰值计算值与实测值基本一致。与计算值相比，实测加速度提升存在滞后渐变性，与模型设置冲剪区初始值有关，且加速度传感器本身特性也受影响，但冲击作用时间一致，计算结果可接受。

位移时程曲线如图6(c)所示，模型的计算值与实测值初始段斜率一致，峰后走势一致。最大位移值相差0.5 mm，由于模型试验模拟月壤颗粒特性铺设不能达到完全平整，因此存在测试误差，故计算模型对最大冲击位移估算误差可接受，可以为足垫尺寸设计提供依据。同时，计算模型峰后回弹略大于实测值，最终位移量估算存在改进空间。综合分析可知，本研究建立的竖向冲击力学模型计算时程与模型试验测试时程的变化规律一致，可以作为足垫-月壤竖向冲击相互作用的估算模型。

5 结论与展望

足垫与月壤动力相互作用的合理、有效预测是着陆器软着陆成功的关键一环。结合室内试验、数值模拟和模型试验测试结果构建了竖向冲击数学力学模型，将月壤状态特性，特别是力学参数的变化，通过精细时程积分算法应用于动力控制方程求解。将测试值与计算值对比，本研究建立的足垫-月壤相互作用竖向冲击力学模型可以较好地估算冲击过程中冲击力、冲击加速度和位移的时程变化规律和峰值，对冲击作用时间亦有较好估算。软着陆过程中，足垫与月壤的实际作用轨迹为三维空间曲线，复杂运动状态下的足垫-月壤系统动力模型的探索将为着陆缓冲机构优化提供重要科学依据。