TNT炸药爆炸场中三波点高度影响的数值模拟研究*

刘 欢 ,徐春冬,张建伟,孔德仁

(1 南京理工大学机械工程学院, 南京 210094; 2 北方华安工业集团有限公司, 黑龙江齐齐哈尔 161000)

0 引言

炸药在空中爆炸时,周围的介质会受到爆轰产物的作用,爆轰产物会强烈压缩周围与其接触的空气,使得压力、温度骤然升高,在空气中形成冲击波[1]。冲击波超压是衡量战斗部毁伤效能的一项重要指标。目前,主要通过地表反射压和自由场超压评价冲击波超压的大小。实际试验中,由于对三波点轨迹并没有清晰的认识,传感器的安装位置也没有一定的规范,使得测出的自由场冲击波压力并不准确,因而不能有效的评估战斗部的威力。而要准确测量自由场冲击波压力,必须了解三波点的轨迹变化规律,才能合理的确定自由场冲击波压力传感器的安装位置。

国内学者对爆炸场中三波点的高度进行了不少研究。乔登江将大量化爆试验结果分析归纳后发现,三波点高度随距离大体变化的经验公式[2]。郭炜等人通过实测炸药爆炸的冲击波超压,研究了三波点的高度,得到了爆炸冲击波传播过程中三波点的轨迹变化规律[3]。段晓瑜等人研究了RDX基含铝炸药三波点高度的数值模拟,得到了3种不同组分炸药空中爆炸的三波点特性[4]。曲艳东等人研究了炸高、药量以及炸药形状对三波点高度的影响,得到了炸高和药量对三波点高度的影响比炸药形状对三波点高度影响较大的结论[5]。但对于装药尺寸、起爆点位置以及反射界面对三波点高度的影响,并没有学者进行相关的研究。

对于带壳炸药爆炸,根据能量守恒原理将其等效为裸露装药的当量计算;其他类型的炸药在空中爆炸时,根据能量相似原理将装药换算成等效的TNT当量[6]。因此,文中将基于AUTODYN有限元分析软件研究TNT炸药在空中爆炸时,柱形炸药的不同装药尺寸、起爆点位置以及反射界面对三波点高度的影响,并拟合出特定工况下三波点的轨迹,为准确测量战斗部在空中爆炸形成的自由场冲击波压力提供参考。

1 三波点的形成

战斗部多数为圆柱形装药,近似为球形装药爆炸。战斗部在空中爆炸时,会产生以球形向外传播的冲击波。由于地面的存在,随着冲击波不断向外扩展,当冲击波与地面接触时,会从地面产生反射,形成反射波。空气冲击波在地面上的反射可根据入射波波阵面法线与反射面法线之间的夹角(入射角θ)不同分为正入射和斜入射。当入射角θ为0时,冲击波在刚性面上发生正反射;当入射角超过某一极限角度时,入射波和反射波会在反射表面合成一个垂直地面并不断向前推进的新击波,也就是马赫波[7-8]。

入射波、反射波和马赫波的交点,称为三波点。图1是炸药在空中爆炸时在地面不同位置处的冲击波压力变化曲线。由图1可知,三波点的高度是以一条上凹的曲线变化的。在实际测试中,若在三波点及其下方布放传感器,测的是马赫波压力随时间变化的曲线;如果在三波点上方布置传感器,将会测得具有两个波峰的压力随时间的变化曲线,其中第一个波峰是入射冲击波的压力随时间的变化曲线,第二个波峰是反射冲击波的压力随时间变化的曲线[3]。

图1 爆炸冲击波的近地面传播示意图

2 数值模拟

2.1 建立模型

以TNT药柱在空中爆炸为试验方案建立物理模型,以此进行数值模拟。整体模型分为空气域和反射界面模型两部分,反射界面选择混凝土,均采用BOX结构。其中空气域为6 m×10 m,混凝土模型为0.6 m×10 m,总体网格划分为330×500=165 000。空气采用多物质Euler算法,混凝土模型采用Lagrange算法,炸药以填充的方式置于空气域中,并在空气域的上表面和前表面施加外围流出边界,即允许空气介质流出。

由于在实际试验中是用自由场压力传感器测量自由场超压。将传感器安装在距地面不同高度处,会测得不同的冲击波压力曲线。因此,本次建模将设置不同高斯点以获得距地面不同高度处的压力时程曲线。其中高斯点1、2分别为距爆心投影点7 m处且距地面高度分别为0.5 m、1 m处测点的位置。为了简化建模过程,采用二维轴对称计算模型。计算模型如图2所示。

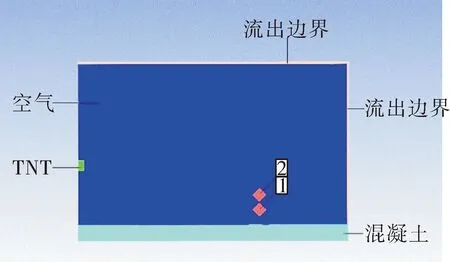
图2 计算模型

由于研究装药尺寸、起爆点位置以及反射界面对三波点高度的影响,因此本次建模过程中,对无关变量TNT炸药当量选取为100 kg、装药离地高度为2 m,TNT药柱的长径比分别为1∶1、3∶1、5∶1,起爆点位置分为顶端中点起爆、药柱中心点起爆和底端中点起爆,反射界面取混凝土地面和刚性反射界面。如图3所示,为TNT药柱3个不同起爆点位置示意图。

图3 TNT药柱不同起爆点示意图

2.2 材料模型与状态方程

TNT炸药的爆轰过程采用JWL状态方程进行数值模拟。JWL状态方程的表达式为:

(1)

式中:P为炸药爆炸产生的压力;V是相对体积;E为单位体积内能;A、B、R1、R2、ω为材料常数,可由试验拟合得到。

由状态方程可知,JWL状态方程由3部分组成,其中第一项对高压段起控制作用,第二项对中压段起作用,第三项对低压段起作用。

TNT的材料输入参数[9]如表1所示,表中ρ为炸药密度,D为炸药爆速。

表1 TNT炸药材料参数

空气介质采用AIR材料模型和Ideal Gas状态方程来描述空气材料的本构关系和状态,Ideal Gas状态方程的表达式为:

P=(γ-1)ρe+pshift

(2)

式中：γ为理想气体常数,取1.4;ρ为密度,取0.001 293 g/cm3;e为内能;pshift为初始压强,取100 kPa。

混凝土模型拟选用材料库中的CONC-35MPA,本构模型采用RHT本构模型,RHT参数[10]选择如表2所示。

表2 混凝土材料参数

2.3 计算结果

由AUTODYN有限元软件运行建立的模型,可以观测到距爆心投影点不同距离处TNT爆炸压力云图。图4为药柱长径比为3∶1,起爆点设置为顶端中点起爆后不同爆心距处的压力云图。从云图上可以直观的看出三波点的高度变化。随着入射冲击波的不断扩展,马赫波向前推进,三波点的高度不断升高。

图4 不同爆心距TNT爆炸压力云图

3 结果分析

3.1 TNT装药尺寸对三波点高度的影响

选取当量为100 kg的TNT,起爆位置均为顶端中点起爆,爆高为2 m,利用柱形装药(长径比分别为1∶1、3∶1、5∶1 )3种方式进行数值模拟。由爆炸压力云图得到距爆心投影点(爆心距)不同距离处三波点的高度,通过MATLAB对所得到的数据进行拟合,得出3种不同装药尺寸下三波点的轨迹变化规律,如图5所示。

图5 不同装药尺寸爆炸三波点的高度对比

由不同装药尺寸爆炸三波点的高度对比图可知,不同装药尺寸柱形药柱爆炸得到的对应三波点高度上升快慢也不同。在同一测点处,不同长径比柱形装药爆炸的三波点高度顺序依次为:1∶1>3∶1>5∶1,表明对于柱形装药,长径比和三波点高度成负相关性。长径比越小,同一测点处,三波点的高度越高。

3.2 TNT装药起爆点位置对三波点高度的影响

选取当量为100 kg的TNT,柱形装药长径比为1∶1,爆高为2 m,起爆位置分别为顶端中点起爆、药柱中心点起爆、底端中点起爆3种起爆方式起爆进行数值模拟。计算得出不同起爆点位置起爆下三波点的轨迹变化规律,如图6所示。

图6 不同起爆位置爆炸三波点的高度对比

由不同起爆位置爆炸三波点高度对比图可知。由于起爆位置的不同,对应的三波点高度上升快慢也不同。在同一测点处不同起爆位置爆炸三波点高度顺序依次为:顶端中点起爆>药柱中心点起爆>底端中点起爆,表明起爆点越高,在同一测点处,三波点的高度越高。

3.3 反射界面对三波点高度的影响

选取当量为100 kg的 TNT,柱形装药长径比为1∶1,爆高为2 m,起爆位置均为底端中点起爆,反射界面分别取混凝土地面和刚性界面进行数值模拟。得到爆炸冲击波在不同界面反射得到的三波点轨迹变化规律如图7所示。

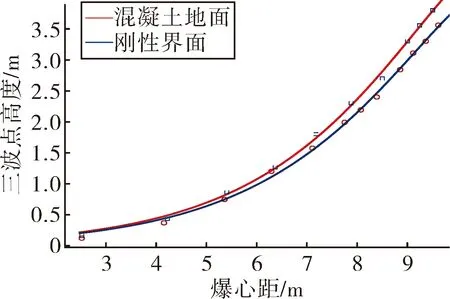
图7 不同反射界面爆炸三波点的高度对比

由于地面的存在,使得爆炸冲击波的冲击传播规律会变得相当复杂[11]。由图7可知,同一测点处,爆炸冲击波在刚性界面上反射三波点的高度大于在混凝土地面上反射三波点的高度。由于两个反射界面的不同,对爆炸冲击波能量的吸收能力也不同。因此,不同界面的反射对三波点高度的影响甚大。

3.4 传感器布设对冲击波超压测试的影响

本次建模设置了不同高斯点以模拟实际测试中传感器的安装位置。高斯点处的压力-时程曲线即对应于实际测试中传感器测得的冲击波压力-时程曲线。图8所示为装药尺寸为3 ∶1,顶端中点爆炸时距爆心投影点7 m处,距离地面高度为0.5 m处的高斯点处的压力-时程曲线。

图9所示为装药尺寸为3 ∶1,顶端中心点爆炸时距爆心投影点7 m处,距离地面高度为1 m处的高斯点的压力时程曲线。

由图5、图8和图9可知,高斯点1在三波点曲线的下方,测得是单波峰,即马赫波压力随时间变化的曲线;高斯点2在三波点曲线的上方,测得是具有双波峰的压力随时间变化的曲线;其中前面的峰值超压为入射冲击波超压,后面的峰值超压为反射冲击波超压,并且反射冲击波超压相对入射冲击波超压较大。由于高斯点2位于马赫反射区,入射冲击波将会在地面不同位置发生不同种类的反射,并使压力不断提高,反射波压力大于入射波压力。在实际试验中,想要更加精确的测得爆炸冲击波的参数,即准确的测得入射波的冲击波压力,需将传感器布设于三波点的上方位置。

图8 压力时程曲线

图9 压力时程曲线

4 结论

文中利用AUTODYN有限元分析软件数值仿真计算了装药尺寸、起爆点位置以及反射界面对爆炸场中三波点高度的影响,对实际爆炸场中准确测量自由场超压具有指导意义。

1)同等装药当量、相同起爆位置下,对于柱形装药,长径比越小,三波点高度越高且三波点的上升趋势越明显。

2)同等装药当量、相同装药尺寸下,对于柱形装药,起爆点越高,三波点高度也越高且增速越明显。

3)不同反射界面对三波点高度的影响较大。实际试验中,反射界面为沙土地面,由于沙土地面的组分比较复杂,在数值模拟中,较难确定其参数。因此,实际试验中沙土地面对三波点高度的影响有待进一步研究。