无人机MEMS加速度计的混合误差补偿

吴镇 宋宇

摘 要：针对惯性导航系统中三轴MEMS加速度计的零位偏移误差、非正交误差、灵敏度误差等多种误差，提出一种基于最大似然估计的混合误差补偿方法，建立三轴加速度计混合误差模型。采集实际惯性传导系统输出数据作为样本，通过梯度下降法进行迭代，以达到算法收敛。该算法对三轴加速度计的混合误差进行隐式求解，其结果包括已知误差与未知误差，是一种包含加速度计全部误差的补偿算法。实验对比误差补偿前后加速度计输出在空间坐标系的分布和在姿态解算中的估算结果，实验结果表明，该算法能对三轴加速度的混合误差进行有效补偿，是一种有效且易于实现的方法。

关键词：惯性导航系统;加速度计;混合误差;隐式求解;空间分布;误差补偿

0 引 言

惯性导航系统（Inertial Navigation System，INS）是无人机的基本组成部分，是无人机维持正常飞行的重要依赖。惯性导航系统多由多个不同类型的惯性传感器件组成，通过多个传感器返回不同数据进行数据融合，从而得到较为精确的姿态参数。加速度计是惯性导航系统中常见的组成部分。常用的MEMS加速度计由于制造工艺与传感器安装等条件限制，加速度计的数据输出中含有固定存在或者周期性存在的噪声，噪声在后续的数据融合、姿态估算中参与计算，将会给后续计算带来较大误差，进而影响导航系统的正常工作。

因此，对未参与数据融合的加速度计的数据进行预处理，是一种目前常见的手段。国内外学者会根据不同需求，对加速度计存在的不同误差进行针对性测量与修正，以达到工作目标。文献[1-3]中，对加速度计进行重力法标定，适合对静态灵敏度误差和零位偏移误差进行测量与标定。文献[4-6]中采用极限学习机、BP神经网络进行误差修正，得出一组隐式补偿参数，利用这组补偿参数对加速度计输出进行补偿。文献[7-8]中对振动状态下加速度计的输出数据进行分析，滤除振动条件下特有的高频噪声。文献[9-10]中针对重力法中需要大型标定台的缺陷，采用椭球拟合方法，进一步简化了误差测量对设备的需求。

本文将针对加速度计的零位偏移误差、灵敏度误差、非正交误差以及轴间串扰进行误差分析，并通过MEMS加速度计传感器进行试验，证明算法的有效性。试验结果表明，该算法可以有效滤除加速度计中的误差，大幅提高加速度计在飞行运动中的测量精度。

1 三轴加速度计误差模型

1.1 三轴加速度计误差分析

文獻[11-13]中描述了三轴MEMS加速度计的测量结果受生产技术与制作工艺的限制，产生的固有误差主要包括零位偏移误差、灵敏度误差、非正交误差以及轴间串扰。

零位偏移误差受制作工艺的影响，无加速度输入时，加速度计也会存在一定非零输出，可以使用常量a0表示，a0∈R3。

灵敏度误差产生的原因在于三轴模拟信号与数字输出比例不完全一致，可以采用一个对角矩阵Sa=diag（Sax，Say，Saz）表示。

非正交误差同样由于工艺限制，因三轴不能实现完全正交而产生误差。正交坐标p其坐标轴为Xp，Yp，Zp，加速度坐标轴为Xa，Ya，Za，两者原点重合，且Xp与Xa重合，如图1所示。

三轴加速度计的轴间串扰原因在于各轴输出间相互影响，可采用一组常数表示。

1.2 三轴加速度计误差参数模型

假定三轴加速度计噪声不随传感器姿态变化，结合上述可以获得三轴加速度计误差模型：

式中：ak为加速度计读数;矩阵S为灵敏度误差与非正交误差;矩阵C为非正交误差矩阵;atrue， k为加速度计的真实值;a0为加速度计的零位偏移误差;na为加速度计的随机误差。

2 椭球拟合算法的误差补偿

文献[14-15]中所述，传统加速度计重力标定方法存在对设备要求高、标定成本高，在普通无人机惯性导航系统上难以应用等问题，本文采用椭球拟合算法对三轴加速度计数据进行补偿。利用加速度计静止时只承受重力作用的特点，使加速度计处于静止但非特定姿态下进行测量。该方法无需借助昂贵的外部设备，通过大量采集不同姿态下的数据进行测定，同样具有较高的精度。

2.1 椭球拟合算法原理

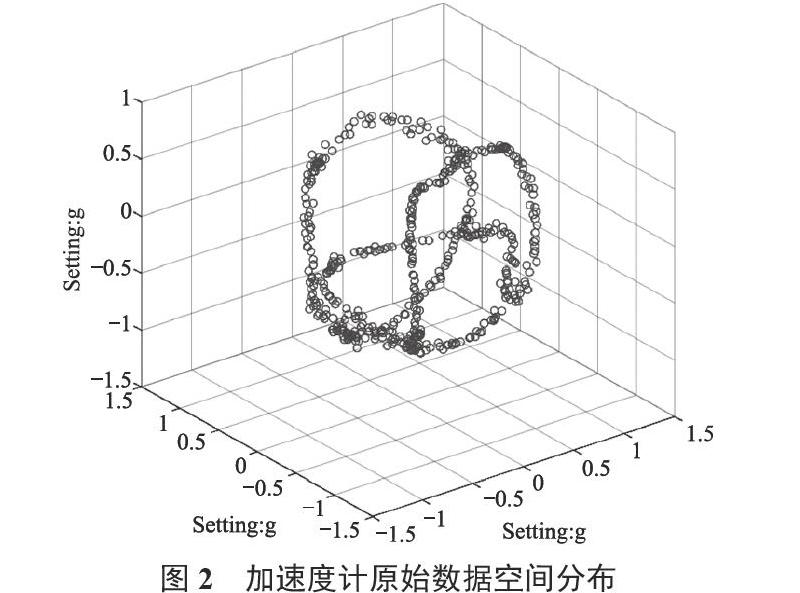
在理想状态下，加速度计处于静止状态时只受重力作用，对各轴的测量值进行合成后将得出一个方向向地心，大小为g的加速度。因此，理想状态下不同姿态下的加速度计输出在空间坐标系上的分布将呈现为一个半径为g，球心与坐标系圆点重合的球形。非理想状态下，在加速度计的误差噪声影响下，加速度计输出数据在空间坐标系上的分布将不再是一个完全的球形，与此同时，对加速度计误差模型产生的超定方程使用最大似然估计法进行椭球拟合，求解得到包括随机误差在内的隐式误差参数，利用该参数对加速度计误差进行混合补偿。

2.2 最大似然估计的椭球拟合算法

本文利用最大似然法求解三轴加速度计误差参数。

2.3 最大似然估计原理

最大似然估计函数在采样的样本总数区域无穷时能达到最小方差，本文利用FPGA作为通信控制手段，自MEMS传感器模块中采集大量样本数据，以实现方差最小化。假定加速度计噪声是一种服从正态分布，方差为σ2a，k，均值为零的高斯过程，则可知加速度计的测量值同样服从高斯分布：

当满足条件||xk-xk-1||≤ε时，迭代完成，算法收敛，此时的xk为较为理想的估计值。式（9）的迭代需要对初始参数进行设定，本文采用最小二乘法对参数进行预拟合，获取初始参数x0。

3 结果与分析

本文采用三轴加速度传感器输出作为样本，以FPGA作为对传感器进行数据采集并与PC端通信的中枢。通过PC端在MATLAB中对三轴加速度计利用上述算法进行误差估计，对比修正前后的数据在空间坐标系下的分布，并将误差数据导入实际惯性导航系统中，对比加速度计输出数据修正前后对姿态解算的影响。

目前常见的三轴MEMS加速度计都具有输出修正功能，即通过人为设置零位偏移误差数值，对三轴加速度计的输出进行预处理。本文中的三轴加速度计传感器中预设零位偏移误差值均为零，以保证三轴加速度计数据的原始性。

为了获取迭代数据的初始值，先采集三轴加速度计不同静止姿态下的数据，选取其中20组数据，采用最小二乘法拟合数据，获取初始参数x0。其三轴加速度计的原始输出在空间坐标系下的分布如图2所示。

将x0作为初始参数，重新采集数据作为样本数据，取惯性导航系统在同一姿态下静止5 s时数据的平均值作为一份样本，采集200组数据样本。在式（9）中进行迭代，结果见表1所列。

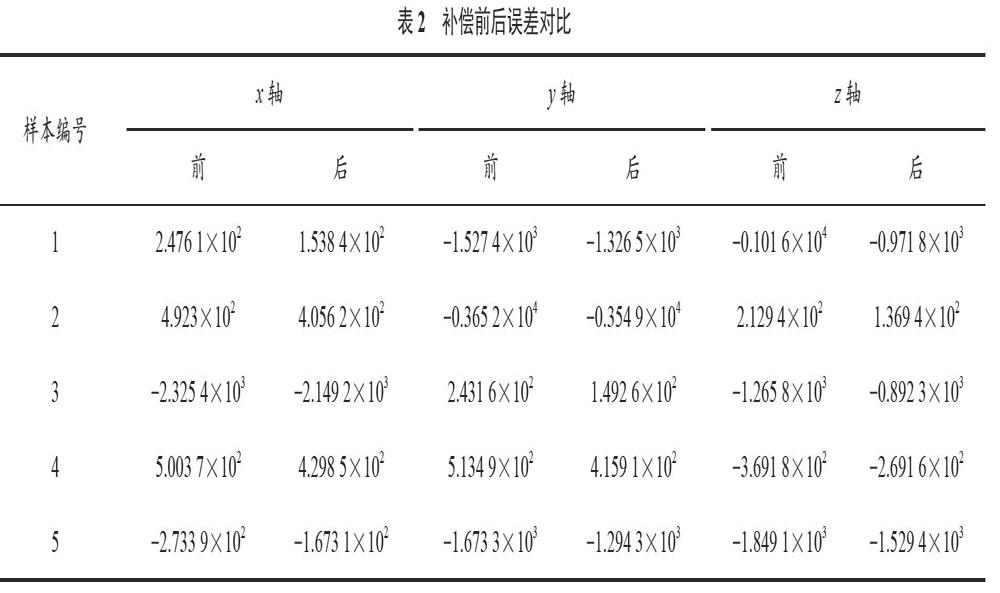
将修正后的结果导入比力方程中进行位移误差实验。理想状态下根据比力方程计算加速度的二次积分结果应为零，具体见表2所列。

4 结 语

本文采用椭球拟合法对三轴加速度计误差进行标定，解决常见重力法标定带来的成本高与条件苛刻等问题，并采用最大似然估计法对误差参数进行隐式求解。有别于传统最小二乘法对指定目标误差参数求解时需假定未指定误差参数为零的做法，采用最大似然估计法对三轴加速度计混合误差进行误差参数求解，其结果能隐式表示三轴加速度计中已知与未知的误差。实验结果表明，本文采用的加速度计误差补偿方法有效、方便。

参考文献

[1] Yu Mingbiao，Cai Tijing.Erratum："Calibration of a rotating accelerometer gravity gradiometer using centrifugal gradients"[J].The review of scientific instruments，2018，89（10）.

[2] RANJBARAN S，EBADOLLAHI S. Fast and precise solving of non-linear optimisation problem for field calibration of triaxial accelerometer[J].Electronics letters，2018，54（3）：148-150.

[3]劉宇，余跃，路永乐，等.MEMS加速度计混合误差标定补偿方案[J].压电与声光，2018，40（4）：589-593.

[4] Xu H E，Zhen Hai Z，Ke Jie L I，et al. Triaxial high-g accelerometer of microelectro mechanical systems[J].北京理工大学学报（英文版），2015（4）：427-431.

[5]杭义军.多旋翼无人机微导航系统误差补偿与信息融合技术研究[D].南京：南京航空航天大学，2017.

[6]石岗.惯性与磁传感器组合航向估计方法研究[D].北京：北京科技大学，2019.

[7]高畅.基于MEMS的IMU误差建模与温度补偿技术研究[D].哈尔滨：哈尔滨工程大学，2017.

[8]刘艳霞，方建军，石岗.基于改进极限学习机的三轴加速度计误差补偿算法[J].传感器与微系统，2019，38（7）：138-141.

[9]王向军，张朝阳，刘峰.基于加速度分离算法的姿态测量方法研究[J].传感技术学报，2018，31（12）：1848-1892.

[10]高爽，张若愚.基于自适应遗传算法的MEMS加速度计快速标定方法[J].北京航空航天大学学报，2019，45（10）：1982-1989.

[11]黄钦文，杨少华，董显山，等.加速度计标定中静态半径误差项的消除技术[J].中国惯性技术学报，2018，26（1）：122-126.

[12]崔智军.微型捷联航姿系统误差分析与补偿[J].仪表技术与传感器，2018（8）：98-102.

[13]鲁瀚杰，刘亚斌，周强.一种基于惯导系统的线加速度计动态性能测试方法[J].兵器装备工程学报，2019，40（12）：165-170.

[14]占伟伟，蔡莉.一种减小加速度计重力法标定中安装误差影响的方法[J].振动与冲击，2019，38（13）：249-252.

[15]于沛，闫禄，张金云，等.振动条件下陀螺加速度计误差抑制技术[J].噪声与振动控制，2019，39（2）：37-41.

[16]李久顺.捷联惯导系统误差抑制及补偿方法研究[D].哈尔滨：哈尔滨工程大学，2018.