应用回归分析改善A面板工厂SiH4日常供应管理

姜昌日

摘要：作为危险化学品的SiH4在液晶面板制造中主要用于化学气相沉淀工艺，是重要的原材料之一。为了生产的安全和稳定，甚至控制成本，需要建立该原材料的日常供应控制管理。用SPC控制图管理日常供应量是非常有效的方法，但是日常供应量数据有时出现失效，无法正确地反映日常供应现状。本文通过回归分析，改善每日供应量的计算方法。建立有效的SPC控制图，并且监控每日供应量是否稳定，受控;及时反馈信息。当出现异常时经过正确的分析和合理的措施，实现供应的安全和稳定，甚至控制成本。

Abstract： SiH4 as a hazardous chemical is mainly used in the chemical vapor deposition process in the manufacture of liquid crystal panels， and is one of the important raw materials. For the safety and stability of production， and even to control costs， it is necessary to establish the daily supply control management of the raw materials. Using SPC control charts to manage daily supply is a very effective method， but the daily supply data sometimes fails and cannot accurately reflect the current status of daily supply. This article improves the calculation method of daily supply through regression analysis. It establishes an effective SPC control chart， and monitors whether the daily supply is stable， controlled， and timely feedbacks information. When abnormality occurs， correct analysis and reasonable adjustments are made to realize the safety and stability of supply and control costs.

關键词：回归分析;供应量;SiH4;SPC

Key words： regression analysis;supply;SiH4;SPC

中图分类号：F253                                       文献标识码：A                                  文章编号：1006-4311（2020）24-0079-06

0  引言

近几年，国家大力推动和支持高端制造业的政策下，面临着市场对电子产品的需求不断升级的现实，作为制造人机交互重要窗口的液晶面板行业而言，其规模持续扩大，产品种类多样化，制程工艺越来越复杂。随着制程工艺的复杂化，工艺中所需要的化学品种类越来越多。这些大多数属于易燃易爆，有毒，剧毒的危险化学品。对于危险化学品的特有的危险性，加上运营过程中需要大量贮存和使用危险化学品的液晶面板工厂来说管理上面对着不小的挑战。其中SiH4属于易燃易爆的工业大宗气体，主要用于化学气相沉淀工艺，是整个制造过程中重要的原材料。按照我国目前的安全生产，消防等法律方面的规范，SiH4供应站属于重大危险源，不仅对其贮存场所的防火设施，贮存和供应的设备，泄露系统等硬件设施和设备有严格的法律要求，还对相关企业在贮存和供应SiH4的日常管理上也有严格的机制要求。每日供应量数据是日常供应管理中重要指标，有效的数据可以直观的反映安全和使用方面的问题，也可以适当的预测未来的使用量，管理库存，使得减少浪费，控制成本的效果。因此需要建立每日供应量的控制管理。

统计过程控制（Statistical Process Control，SPC）是一种借助数理统计方法的过程控制工具。根据中心极限定理，检测量的统计值一般都服从正态分布;根据正态分布3δ准则计算上控制线（Upper Control Limit，UCL）与下控制线（Lower Control Limit，LCL），统计值落入上下控制线外的概率为0.27%，按照小概率不发生原理，当此情况出现则认为过程处于不稳定失控状态[1]。这种控制图可以对供应情况进行分析，根据反馈信息及时发现系统性因素出现的征兆，采取适当的改善措施消除异常影响;使得过程始终维持在仅受随机性因素影响的受控状态，从而达到供应的安全和稳定，控制成本的目的。统计过程控制理论的研究虽从加工过程开始，但其研究成果适应于各种过程，如设计过程，管理过程，生产过程，服务过程;统计过程控制已成为企业质量管理必不可少的工具和质量保证手段。液晶面板行业的Samsung Display，LG Display，京东方等面板企业早在20实际90年代开始引进6δ质量管理理论，并且把统计过程控制理论运营到制程过程的各领域。特别是设备参数设定，工艺能力评价中广泛利用。

本文以问题为导向，通过回归分析提高SiH4每日供应量数据的有效性，在拟合值的基础上建立“单值-移动极差控制图”，有效控制SiH4供应过程，根据反馈信息及时发现系统性因素出现的征兆，采取适当的改善管理消除异常影响。使过程始终维持在仅受随机性因素影响的受控状态，从而达到供应的安全和稳定，控制成本的目的。

1  SiH4供应量管理中存在的问题

1.1 SiH4供应系统构成及管理现状

A工厂SiH4供应系统主要由SiH4供应站内的长管拖车，BSGS，连接到生产设备的管道设施，生产厂房内的VMB和泄露探测器等部分构成。其中，SiH4供应站是甲级防火等级的生产附属建筑。长管拖车是储存高压SiH4的容器，BSGS设备主要作用是快速降压SiH4的压力，实现稳定的供应压力。降压后的SiH4通过双重管道，在VMB设备进行分配管路并供应到生产设备[2]。SiH4供应系统请见图1。整个供应系统每隔30米距离安装了泄露探测器的探测感应器，探测感应器主要利用化学反应检测气体泄露，再把光信号转化为电子信号的方式工作。另外，整个系统采用SSM集成信息系统实时监控供应和泄露的状态。

对于SiH4供应量的管理，每日供应量数据的计算和共享是主要管理对象。SiH4系统供应量的计算是通过信息系统收集的每日凌晨0点的SiH4供应站室内温度和安装在BSGS管道中的压力表的压力值来计算。由于BSGS与长管拖车是紧密连接，并且相关压力表都符合测量要求;测量数值能够精准的反映容器内SiH4的压力值。收集数据后，利用范华德方程[3]计算当日0点的容器内剩余重量。最后，减去前天0点的剩余重量，得出SiH4的日供应量。图2是某月供应量的趋势图。

可以看出，某月供应量数据波动大，供应量为0的天数多达17天。但是经确认当月每天都使用SiH4，说明现有的供应量数据无法反映实际使用情况，数据严重存在无效性。因此，以现有的数据不能进行过程控制管理。

1.2 供应量问题分析

表1中剩余重量值是以温度测量值和压力测量值为自变量，通过范德华方程计算的数据。当日供应值是由当前剩余量减去前天剩余量而得出的差值。显然，当日重量值中的存在负数。经确认现场统计人员因负数没有现实意义，直接修改负的数值为0。因此计算结果为负数的数据导致供应量为0的无效结果。当日供应值不仅是负值，并且偏差也很大。原因主要是无法直接测量重量数据的情况下，采用范德华方程计算过程中，本应该利用在压力一定时重量与温度负相关关系或者温度一定时重量与压力的正相关关系，但是当前环境中很难控制温度或者压力相对稳定的状态;另一个原因是当月产量的波动也影响了剩余重量值的计算。因此，计算剩余重量值过程中适当控制温度，压力，使用量的波动可能成为一种理想的解决方法。

2  数据研究与回归分析

2.1 数据研究

由于现有可收集的产量值，温度测量值，压力测量值等数据不能够计算出有效的每日供应量，所以对已收集的数据进行适当的变化，使得温度和使用量的波动尽可能得到控制。

t日的？驻Pt实际上t日，凌晨0点时的温度下，剩余重量值没有变化时的压力P′t与剩余重量值按照产量变化时的压力Pt的差值。计算中温度都统一使用了t日，凌晨0点的测量温度，很大程度上控制了温度的变化。在温度和体积相对稳定的情况下，压力与重量成正相关关系。因此，？驻Pt与Mp成正相关关系。而通过式（3）得知，Mp与产量Ct是存在正比关系;所以，？驻Pt与Ct可能存在正相关关系。

2.2 数据收集

以过去某8个月的数据为基础，利用2.1数据研究章节的6个式得出？驻Pt。其中，单位产量的平均期望使用量U值是根据生产部门的相关生产数据和实际生产经验得出。U值的验证不是本文研究范围，因此不进行相关验证;只利用产量与原材料的使用量成正比，并且存在单位产量平均期望使用量的一般性结论。由于化学气相沉淀是关键工艺，工艺中参数都有长期稳定性，所以假设期望值U值具有稳定性，长期不变。表2是某8个月统计量的部分数据。

2.3 回归分析

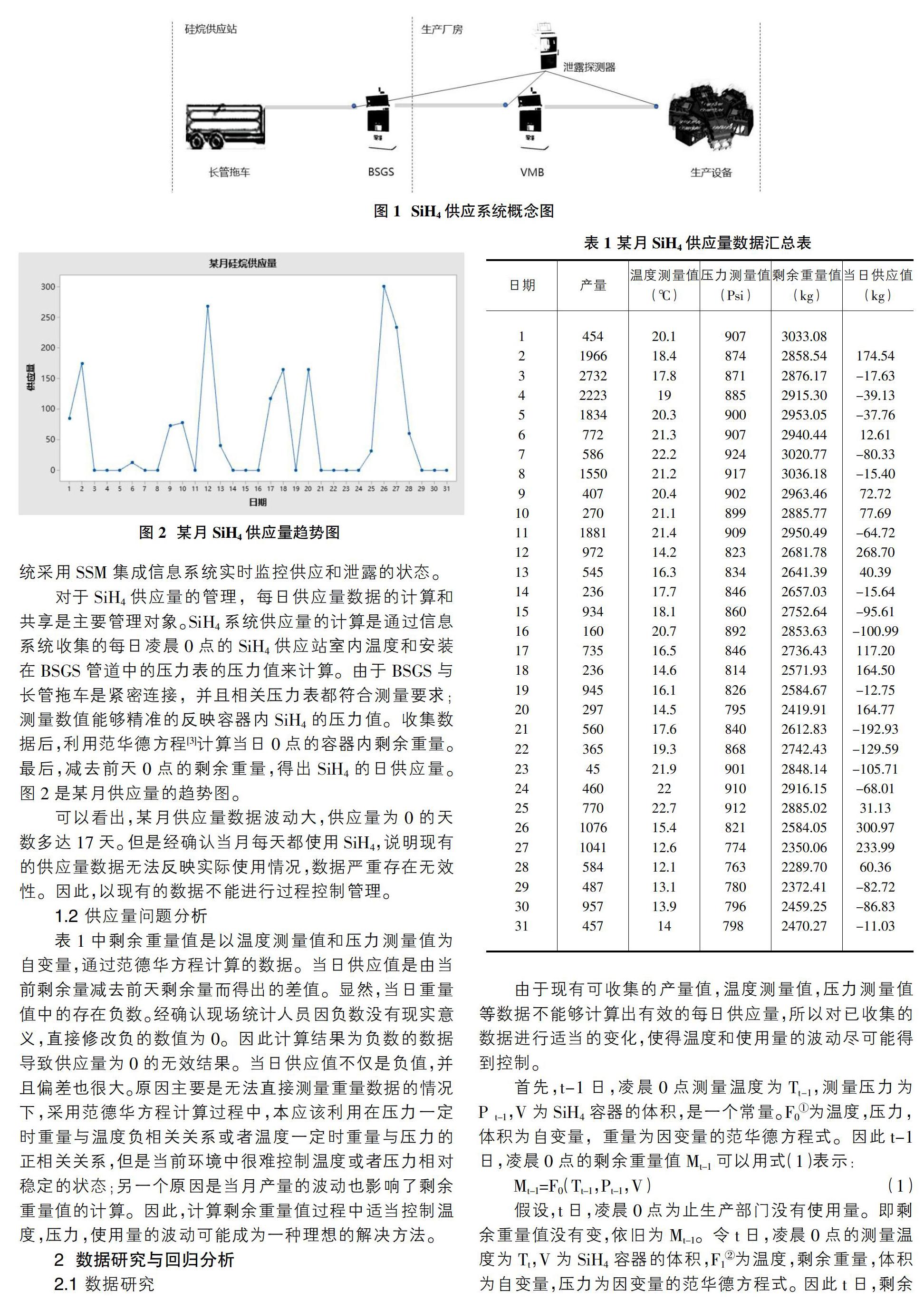
首先，对？驻Pt与Ct进行相关关系验证，图3是通过软件得出的结果。关系系数R为0.946说明？驻Pt与Ct之间存在强正相关关系，需要有必要进一步的研究。

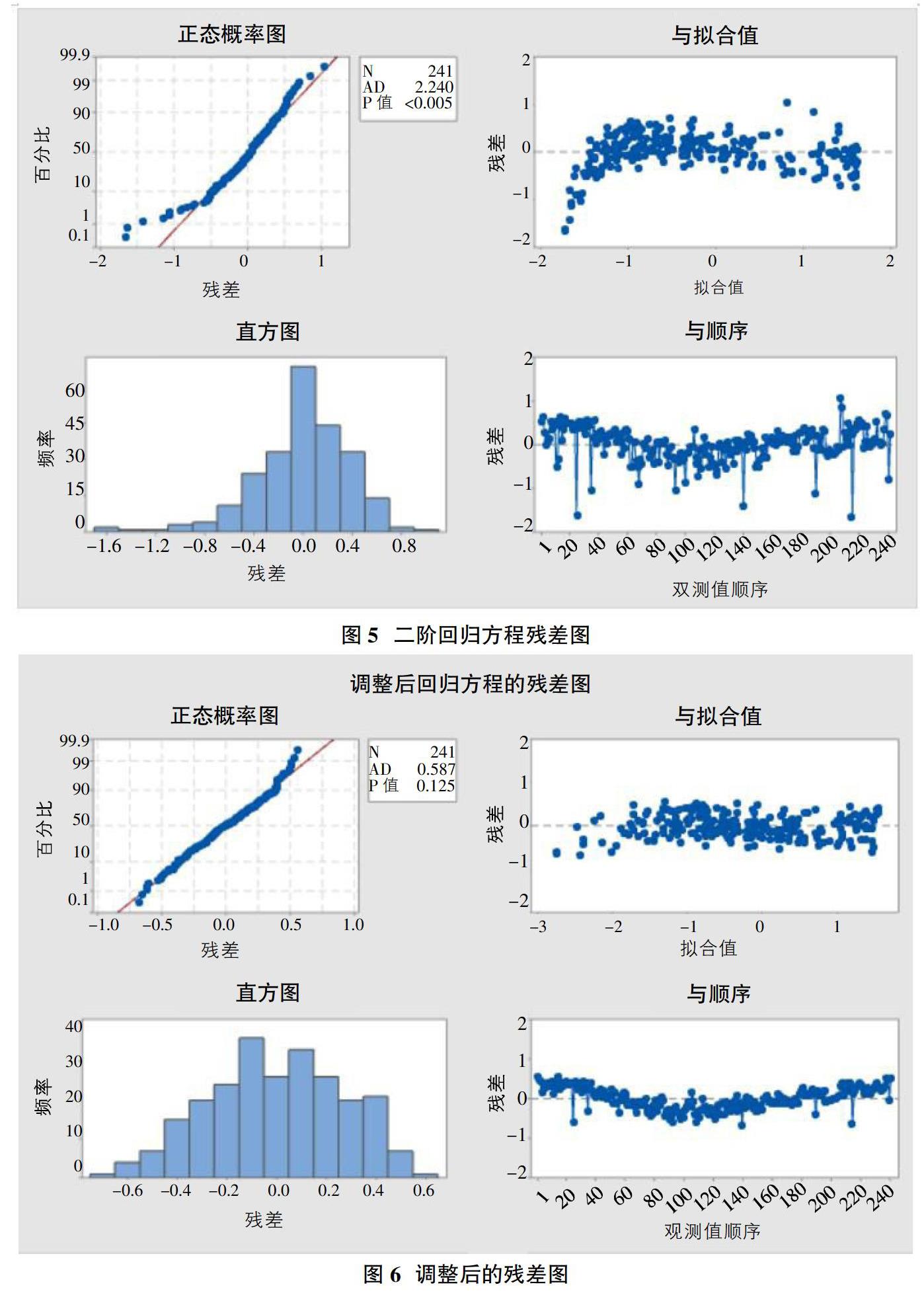
图6是调整后的残差图。正态概率图中可以看出P值为0.125大于0.05，说明残差服从正态分布。残差与拟合值的散点图中可以看出，残差值基本上随机分布，没有异常形态。

残差与顺序的散点图中可以看出，残差略微具有自相关性;但是实际数据为压力值，压力受温度波动影响，温度呈现一定的时间序列模型。考虑作为自变量的产量对回归方程已经贡献多达93.7%的信息量，再加上最终控制管理的对象为每日供应量即重量。综合上述情况，现存在的自然对数转换后压力差值残差的自相关性可以视为白噪声，即非控制因素。

3  检验模型

3.1 模型的现实意义

3.2 模型预测

以1.2章节的表1的数据为基础，利用3.1拟合回归的模型，重新预测存在问题月份的每日供应量。表3为预测结果。

预测结果显示与实际情况一致，每日都存在供应量数据。比起改善前17天的供应量数据为0的统计结果，数据有效性有了显著的进步。经过生产部门和采购部门的数据验证，此预测数据基本上符合同一时期的采購量和使用量的预估数据。因此，通过回归模型得到的预测数据可以使用到日常供应管理过程。

4  控制管理

改善后的每日供应量数据可以反应实际生产情况。由于供应量自身的管理特征，一个统计周期内只有一个数据，是属于子组只存在一个观测值的情况。可以采用“单值-移动极差”（x-Rs）控制图分析供应过程的统计受控情况[5]。

根据供应量数据的实际意义，采用控制图上有一个点位于控制线以外的规则1和连续6点递增或者递减的规则3为供应是否受控状态的判断规则。图7为3.2章节预测数据的单值-移动极差控制图。

控制图中可以发现，第三天的供应量超过了上限值。经确认，这天由于反品加工量多，新产品开发测试的安排，使用量增多;也比前天供应量的差值略大，从而导致发生了失控状态，控制管理的作用在于通过每天分析最近31天供应量的单值-移动极差控制图，根据其反馈信息找出失控出现的原因，并及时改善处理;减少不必要的浪费，从而完成适当供应，达到供应的安全和稳定，甚至控制成本的目的。

5  结论

SiH4日常供应量数据存在无效现象，不能够反映实际生产使用情况。由于温度，压力，使用量等因素的同时变化，导致已有的计算方法的结果会出现负数。通过范华德公式的推导，有效控制温度和使用量的波动，利用压力差和产量的正相关关系，拟合出回归方程。并通过回归分析和残差分析完善模型。通过模型检验，验证了改善后的预测数据比改善前的数据更具备有效性，也基本上符合与生产和采购的预估数据。根据供应量数据的实际意义，采用单值-移动极差控制图分析供应过程。对于失控进行原因分析，并及时进行改善措施。今后，可以采用同样的方法持续监控SiH4的供应量。

本文的SiH4每日供应量计算方法和控制图分析方法对于其他高压气体的供应量控制具有一定的扩展性。

注释：

①F0为荷兰化学家范德华研究了许多气体之后，提出了修正气体方程式，其形式为：P+a（V-nb）=nRT，其中a，b为范华德常数，P为压力，V为体积，T为温度，n为摩尔质量，R为比例系数。

②F1为F0推导公式，其形式为：

参考文献：

[1]林文康，吴丽娜.基于ARIMA模型烧结脱硫烟气指标的统计过程控制[J].烧结球团，2019，44（05）：76-82.

[2]李建辉，张宁，李爽，许浩宾.浅谈特气的安全运行与管理[M].中国新技术新产品，2017（06）.

[3]张祖德.无机化学[M].二版.中国科学技术大学出版社，2014：8-9.

[4]威廉·M门登霍尔，特里·L.辛西奇.统计学[M].六版.机械工业出版社，2018：415-416.

[5]賈新章，等.统计过程控制理论与实践——SPC、Cpk、DOE、MSA、PPM技术[M].电子工业出版社，2017：78-79.