基于KPCA与KFDA的国六柴油机EGR系统故障诊断

王彦岩，马腾飞，沈义涛，张正兴，郝宝玉

(1.哈尔滨工业大学(威海)，山东 威海 264209;2.一汽解放商用车开发院，吉林 长春 130011)

废气再循环(EGR)技术是柴油机降低排放采取的重要技术手段之一，随着国六排放标准进一步提高，系统的复杂性也大大增加，恶劣的工作环境更易使EGR系统出现故障，从而对排放性及经济性带来较大的影响。同时随着柴油机的智能化，大量传感器的使用使得信息融合技术应用更加广泛，其通过对从多个信息源获取的数据进行关联和综合来完成最终所需决策，可提高故障诊断的准确性。在此基础上，基于数据驱动的故障诊断方法被广泛应用，且目前正处于学术界和工业界全面重视的阶段[1]。目前柴油机在线诊断是通过车载自诊断系统OBD(On Board Diagnostics)实现故障检测，此方法对于电子类故障有较好的诊断效率和精度，但对机械故障的诊断精度低，机械故障更多依赖于线下人工诊断，已经无法满足车主越来越高的需求[2-3]。SAE的IVHM(Integrated Vehicle Health Management)标准委员会定义了IVHM能力水平的进展，即从0级的基本“不自动化”到最终5级的“自适应健康管理”的目标[4]，而对数据的综合处理在此过程起着至关重要的作用，也将是未来智能化发展的基石。

1 诊断方法及原理

主成分分析法(Principal Component Analysis, PCA)和Fisher判别分析法(FDA)都是基于数据驱动的多元统计方法，PCA是目前应用最广泛的降维技术[5]，Fisher判别是一种常用的数据分类技术，已应用于许多工业过程的故障检测和分类[6]，但在柴油机故障诊断方面以上两种方法的使用并不多见。柴油机的结构及工作特性均十分复杂，EGR系统的过程变量众多，各变量之间往往呈现出强耦合性和非线性[7]，无法根据变量变化直接获得故障结果，故本研究在PCA和FDA的基础上引入了核(Kernel)函数，组成了KPCA与KFDA相结合的多变量故障诊断方法。对于不同EGR故障下的过程数据，监测参数众多，其数据的结构特点和分布特性具有差异性，从整个多元统计的角度来看，多变量的监测与分析弱化了部分数据之间的耦合性，这也是此类方法在大数据分析及机器学习领域的一个特点。

KPCA与KFDA相结合的柴油机EGR故障诊断方法原理见图1。首先对数据进行采集，确定用于诊断的特征变量，然后提取出典型工况下各类故障的数据样本，利用KPCA对高维数据样本进行降维，再根据样本故障类别定义数据标签，将数据分为训练集和测试集，分别用于训练及测试KFDA分类器，最终通过KFDA分类器输出测试集的数据标签，确定故障类型，完成柴油机EGR系统故障的诊断。结果表明，与未使用核函数的线性方法(PCA+FDA)相比较，此方法具有更高的诊断精确度。

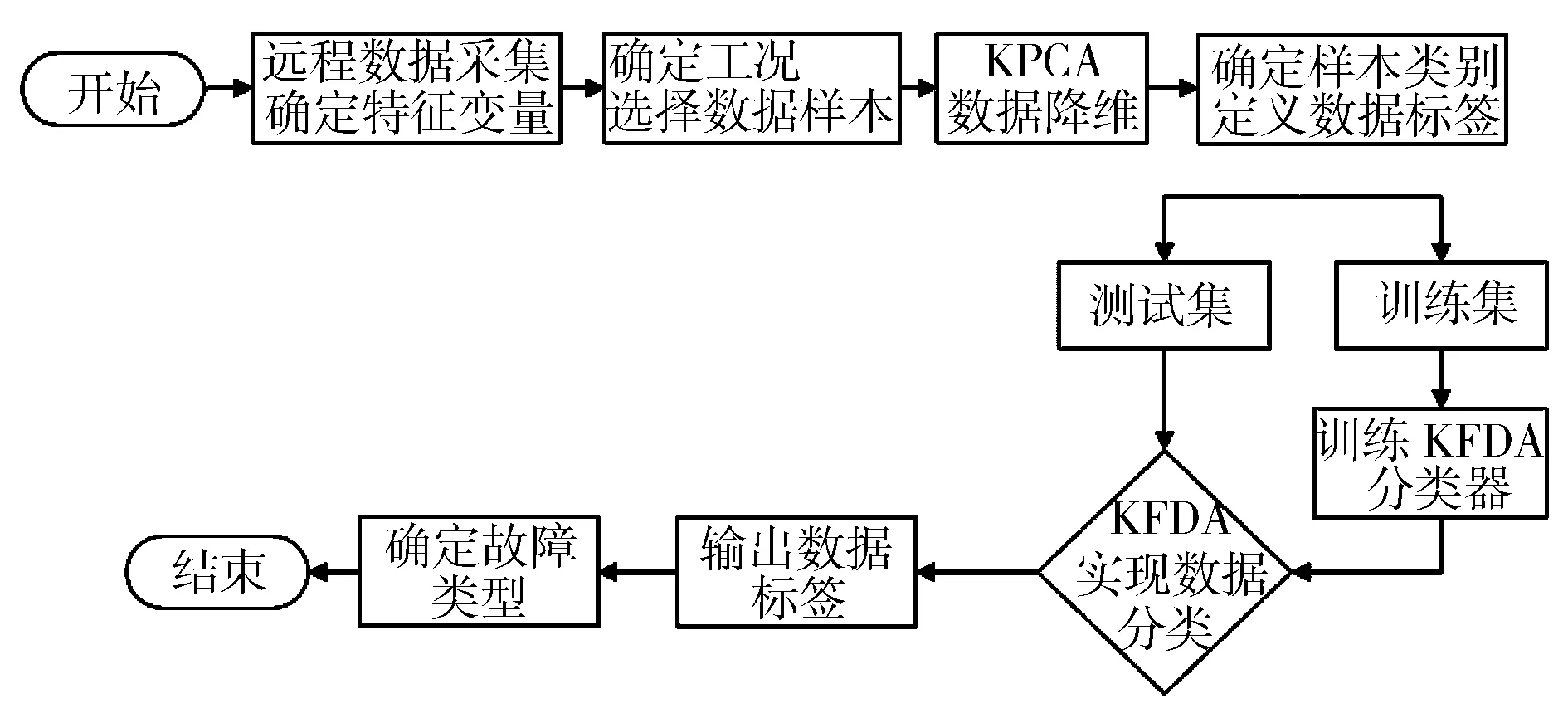
图1 KPCA结合KFDA故障诊断原理

2 算法

2.1 核函数

核函数可增强对非线性数据的处理能力[8]，其主要思想是将原始输入空间里的非线性数据映射到高维空间中，将非线性问题转换为高维空间里的线性问题后再进行线性求解，思路见图2，并且不同的核函数在处理不同的非线性数据时具有各自的效果及独特的优点[9-10]。

图2 核函数映射示意

常见核函数有以下几种：

线性核函数：

K(x,y)=xTy+c。

(1)

式中：c为常数。

多项式核函数：

K(x,y)=(axTy+c)d。

(2)

式中：c为常数；d为多项式阶数。

高斯核函数：

(3)

式中：σ为函数的宽度参数,控制函数的径向作用范围。

2.2 KPCA

KPCA可以实现降维与提取非线性数据特征的双重目标[10]。设原始数据集有n个样本数，m个维度，经核方法将数据映射到高维空间后，计算其协方差矩阵，求得协方差矩阵的特征值λ及特征向量p，存在相关系数ai(i=1,2,…n)，使得

(4)

进一步简化得

nλa=Ka。

(5)

式中：K为n×n的核矩阵;a为核矩阵K的特征向量。

Kjk=K(xj,xk)=φ(xj)Tφ(xk),

(6)

a=[a1,a2,…an]T。

(7)

通过求解核矩阵K，将特征值从大到小排列，以85%的累积方差贡献率标准[11-12]，选取各特征值对应的特征向量组成特征空间的降维矩阵，新数据x在特征空间中为

(8)

2.3 KFDA

(9)

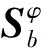
(10)

(11)

引入内积核函数替代特征空间里的内积计算：

K(xi,xj)=kij=φ(xi)φ(xj)。

(12)

wφ可以表示为

(13)

KFDA的目标可转换为

(14)

其中：

(15)

(16)

ξx=[K(x1,x),…,K(xN,x)]T。

(17)

进行广义特征值分析得到:

(18)

式中与特征值λ对应的特征向量a就是投影方向。求出投影方向后，确定分类的判别阈值yφ：

(19)

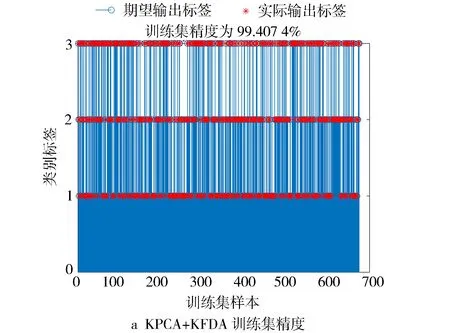
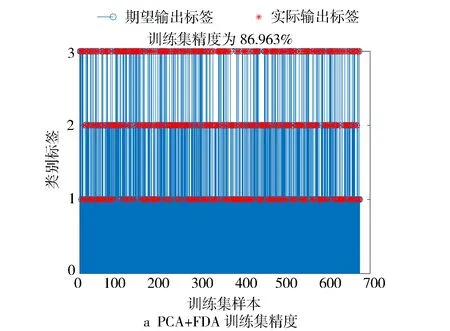
对于新数据x*的投影点y，若y>yφ，则新样本属于第0类；若y

3 故障监测及数据采集

对10辆搭载国六排放标准柴油机的车队进行远程在线监测，实时采集车辆运行状态、ECU控制参数等共计100个参数，样本采样时间间隔为1 s，形成了车辆运行参数的大数据样本集。试验中单车行驶里程为5 000 km，监测中柴油机EGR系统出现了2个频发故障，故障1为EGR冷却效率低，故障2为EGR流量低，形成了一定数量的故障样本。由于EGR率由新鲜进气量与再循环废气量决定，又会受到温度、压力等的影响，故选择进、排气系统中的11个监测参数作为EGR故障诊断数据模型中的特征变量，分别为新鲜进气量、总进气量、进气歧管压力、进气歧管温度、排气流量、涡前排温、中冷后温度、EGR温度、EGR压力值、EGR位置输出值、EGR压差输出值。经过多次诊断试验，结果证明能够利用这11个变量实现对不同故障数据的有效识别，可以达到对故障进行诊断的需求。选取了柴油机运行中常出现的两个典型工况(工况1：转速为1 400±50 r/min，扭矩为2 200～2 400 N·m；工况2：转速为1 200±50 r/min，扭矩为2 200～2 400 N·m)作为诊断工况。

4 故障诊断

EGR系统中选择的11个特征变量与故障之间无线性对应关系，同时PCA是一种线性算法[15-16]，不能有效抽取出数据中的非线性结构特征[7]，而KPCA方法可以很好地解决此问题[17-18]，且它提供的特征数目更多、特征质量更高[19]，对于通过信息融合后的复杂数据源仍能够有效完成数据降维。同理，针对非线性问题，KFDA可以更好地对非线性数据样本进行处理[7-8,20-21]。经过使用不同核函数进行多次试验，最终确定KPCA中的核函数使用线性核函数，KFDA中的核函数使用高斯核函数。

将图1的诊断方法用于EGR系统故障诊断。故障诊断流程基于Matlab平台，采集到数据后为避免噪声干扰进行了去噪处理，然后通过Matlab软件载入数据样本，每个样本均由11个过程变量的监测值组成；利用KPCA算法对数据实施降维，然后对正常状态、EGR冷却效率低、EGR流量低状态下的三类数据定义类别标签，分别为1、2、3，在此基础上利用KFDA算法对训练集数据训练得到分类器；将测试集数据输入分类器后，分类器根据判别阈值输出每个数据对应的类别标签，结果以茎状图的形式进行可视化，可根据茎状图里的类别标签确定样本数据对应的故障状态，完成诊断。

选取工况1正常状态、EGR冷却效率低、EGR流量低状态下的数据样本各300个，对数据进行降维并标注类别标签后按照3∶1的比例随机分为训练集和测试集，利用训练集数据进行KFDA分类器训练，最终分类器的训练集精度达到99.41%。然后利用训练好的分类器对测试集数据进行分类，测试集精度达到99.11%，结果见图3。

图3 工况1 KPCA+KFDA诊断结果

而PCA+FDA组合成的线性方法，对于柴油机参数中的非线性数据不能很好地进行判别，其训练集精度为86.96%，测试集精度只有88%，结果见图4。

图4 工况1 PCA+FDA诊断结果

同理，选取工况2正常状态、EGR冷却效率低、EGR流量低状态下的数据样本，样本数分别为161、187、183个，降维并标注类别标签后按照3∶1的比例随机分为训练集和测试集，利用训练集数据进行KFDA分类器训练，最终训练集精度达到95.98%。然后利用分类器对测试集数据进行分类，测试集精度达到了90.98%，受到工况及样本数量的影响，其精确度略低于工况1，结果见图5。而PCA+FDA组合成的线性方法，其训练集精度为82.41%，测试集精度为87.97%，结果见图6。

图5 工况2 KPCA+KFDA诊断结果

图6 工况2 PCA+FDA诊断结

由诊断结果可知，在原有线性方法的基础上结合核函数，可以有效处理EGR系统中的非线性过程变量，进一步提高故障的诊断精确度，并能够较为准确地诊断出EGR系统的冷却效率低故障和流量低故障。

5 结束语

针对柴油机EGR系统的非线性问题，引入了核方法，可提高对EGR系统非线性问题的处理能力。提出基于KPCA与KFDA结合的柴油机EGR系统故障诊断方法，对EGR冷却效率低和EGR流量低两类故障多次验证后，诊断精度最高达到99.11%。将此方法向柴油机其他系统拓展，对于建立柴油机整机在线健康管理系统，提高柴油机运行可靠性，具有重要意义。