一种国际跳棋的博弈系统研究

桂义勇

（北京信息科技大学 计算机学院， 北京100101）

0 引 言

一直以来人们都想让计算机来战胜人类，从战胜世界棋王卡斯帕罗夫的国际象棋深蓝到战胜李世石的围棋博弈程序AlphaGo［1］。 人们一直以来都在为了这个目标而不懈努力。 国际跳棋是在全世界热门的一个棋种，因为其简单的规则和多样的走棋方式在世界范围内备受欢迎。 目前国际跳棋8×8 的研究已经被完善，但10×10 的研究还在进行中。 本文研究的是国际跳棋10×10，通过棋盘界面的构建、棋盘局面的评估和对局面的搜索，实现了一个国际跳棋的计算机博弈系统。

1 国际跳棋规则简述

1.1 棋盘表示

西洋跳棋的棋盘为10×10 黑白相间的方格棋盘，每个玩家的右下角应该是白色格子，如图1所示。

黑格为合理棋位，棋位统一编码如图2 所示。开局时黑白双方的棋子各摆在棋盘靠近自己一方的4 行黑格当中，如图3 所示。 黑方先手，然后双方轮流走动自己一方的棋子。

1.2 走棋规则

在整个对弈过程中，浅色格子是用不到的。 棋子自始至终都是在黑格子中沿对角线方向移动和停止。 对弈的目标是将对方所有的棋子吃掉或者形成一个局面逼使对方棋子不能移动。

图1 国际跳棋棋盘Fig.1 Checkers board

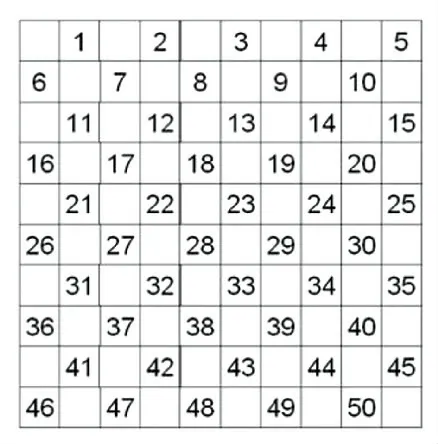
图2 棋盘统一编码Fig.2 Checkerboard unified coding

图3 开局的布局Fig.3 Start layout

只要对角线方向邻近的黑格内有对方的棋子并且再过去的黑格是空位，就可以跳过对方的棋子并将对方棋子吃掉。 如果没有跳吃的着法，就只能沿对角线方向前移一格。 当某一着法结束之后才将吃掉的棋子从棋盘上移出，任何被吃掉的棋子虽然还没有从棋盘上移出也不许再跳经该棋子。 跳吃的时候，在具有多种选择的情况下，必须选择吃子最多的着法。

任何一个棋子到达对方底线便立刻加冕，从此便成为“王”。 只有停止在对方底线上的棋子才能加冕。 所以，如果一个棋子在跳吃过程中行进到底线又离开了底线，最后没有停止在底线上，则该棋子不能升王。 王可以在对角线方向上移动任意多个空格。 同样在跳吃的时候，王可以跳过对方棋子前后任意数量的空格。

2 国际跳棋博弈系统的结构设计

2.1 博弈系统设计

国际跳棋博弈系统主要由两个方面组成，博弈平台和博弈算法。 计算机博弈系统的目的是让计算机能够像人一样进行分析、判断和作出决策的智能系统。 博弈平台的主要功能是信息的传递、规则判断和界面显示等；博弈算法主要研究的是搜索算法、局面评估算法和走法生成等工作。 博弈算法是整个博弈系统中的核心部分，是一个博弈系统的大脑［2］，决定了系统的能力。 博弈系统架构如图4 所示。

图4 博弈系统架构图Fig.4 Game system architecture diagram

架构设计完成后，需要进行博弈流程的设计。根据国际跳棋的规则对弈双方需要交替下棋，每次交替后换手。 在每次下棋时搜索棋子位置并返回到前端的界面，显示能够下棋的位置，行棋结束后更新棋盘界面。 如在连续跳吃的情况下，每次行棋时先不换手，当连续跳吃结束之后再轮到对方下棋。 博弈流程如图5 所示。

图5 对弈流程图Fig.5 Game flow chart

2.2 数据结构设计

结构设计包括：棋盘存储类型的设计、棋盘、棋子以及对棋盘规则的实现。 变量的定义对程序的编写有着重要的作用，合理设计变量不仅能够提高程序的可读性，而且还能在之后对程序的维护中提供更加清晰标识。 棋盘通过一个二维矩阵来记录局面，其中黑子表示为1、黑王表示为10、白棋表示为－1、白王表示为－10。 这种设计的方式在后面的评估函数设计时，便于评估棋盘中棋子的棋力。

3 系统后端详细设计

3.1 局面评估算法

不同的走棋方法就会产生不同的局面，如何对棋盘局面进行有效的评估，判断当前的下棋方法是否对己方有利，是评估函数需要考虑的地方。 如果设定好了博弈程序的评估函数，那么博弈模型下棋的方式就会按照设计的权重来对所有可以下棋的位置进行判断，选择对己方利益最大的位置。 因此一个评估函数的优劣在很大程度上决定了计算机博弈程序的好坏。

在国际跳棋中吃子的策略往往是最有效的策略。 进攻可以把棋子的可活动空间变大，让更多棋子能够活动。 棋子防守策略会让棋子的可活动空间减少，使局面变得被动。 王棋的数量在很大的程度上决定了棋局的输赢。 如果能够形成王棋，则该方对棋盘的掌控就会有很大提升，棋子活动的范围也能大幅度增加。 通过对国际跳棋的分析，找出了6个能够代表棋子能力的因子： x1己方棋子数量；x2对方棋子数量；x3己方王棋数量；x4对方王棋数量；x5己方可以跳吃的棋子个数；x6对方可以跳吃的棋子个数。 通过对评估函数的设计，对棋盘局面的好坏进行判断。 评估函数为：

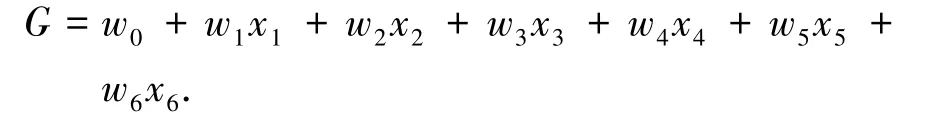
其中：w0是一个固定的偏移量，w1～w6是每个因子的权重。 x1～x4可通过棋子列表得出，参数x5和x6可通过棋盘的走子算法得出。

3.2 棋盘价值矩阵

棋子分布在棋盘的不位置会有着不同的价值，分布在棋盘中心的棋子能够活动的空间也往往最大。 经过人们对国际跳棋的认识，总结出了棋盘对应位置的价值矩阵，通过对当前棋子落点位置计算出当前局面的棋盘价值。

黑棋的价值矩阵为

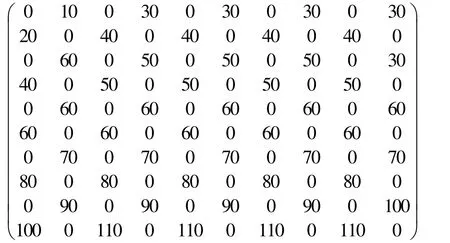
白棋的价值矩阵为

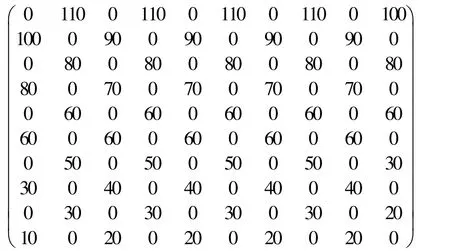
通过对两种方法相结合得到局面评估函数：

如果只是通过静态评估算法会造成送子太多、不积极称王和兵落后等问题。 对这些问题通过增加棋子的价值矩阵，能够有效的改善静态评估算法出现的问题，对己方的棋子起到保护防守的作用；能有效地向对方发起进攻，提高了棋子称王的积极性；能够对局面的棋子的移动趋势更加准确和有效，选择出最优的落子方法。

3.3 搜索算法

搜索是一个计算机博弈程序的核心，在国际跳棋中搜索算法有很多，比如Min Max 搜索、负极大值搜索和Alpha Beta 搜索等等。 Min Max 算法又叫做极大极小算法［8］，是一种找出失败的最大可能性中的最小值的算法，即最小化对手的最大收益的算法。极大极小算法是一种穷尽搜索方法的典型代表，通过搜索在所有的走法中找到最优的走子方法。

Alpha Beta 树搜索算法是一种在Min Max 算法的基础上改的博弈搜索算法，是一种深度优先的搜索算法。 Alpha Beta 算法与Min Max 算法相比最大的优点是增加搜索的深度。 Alpha Beta 算法通过减少博弈树的分支，将搜索资源用于更有希望的子树上的方法，来增加搜索的深度，当遇到没有必要再去搜索的子树时进行剪枝。

图6 Alpha Beta 剪枝算法Fig.6 Alpha Beta pruning algorithm

4 结束语

博弈程序设计主要由3 个部分组成，棋盘的结构设计、评估函数的选定和搜索算法。 棋盘结构的设计是通过二维矩阵来就棋盘局面进行保存，移动棋子是通过对棋子类型的判断，来选择棋子的走子选择。 评估函数通过对棋盘局面诸多因素的判定，得出当前局面的优劣情况，以此来提高模型对棋局的掌控状态。 在对棋局进行搜索时总希望己方处于更加有利的地位，就需要加深搜索的深度。但是随着搜索层数的加深，搜索的局面也会成指数级别的增加。 然而对于一些局面没有必要再去对它们进行搜索。 本文选择Alpha Beta 剪枝算法，从而增加搜索的层数，提高博弈模型的强度。

虽然本文的设计达到一定的使用效果，但还有待进一步完善。 如评估函数的设计还较为朴素，静态评估考虑的棋盘因素有限。 在设计博弈模型时还可采用深度学习和强化学习相结合的方法；可采用Alpha Zero 的方法来对博弈模型进行自博弈训练，通过大量的自对弈让模型通过自我学习的方式提升棋力。