深水钻井隔水管外多普勒超声波气侵早期监测方法

尹邦堂，林英松，王志远，孙宝江，刘书杰，孙金声，侯健，任美鹏，王宁

（1.非常规油气开发教育部重点实验室，山东青岛 266580；2.中国石油大学（华东）石油工程学院，山东青岛 266580；3.中海油研究总院有限责任公司，北京 100028）

0 引言

深水钻井过程多钻遇异常高压地层，气侵易发，甚至诱发严重井喷，如2011年美国深水地平线钻井平台井喷[1]，不仅造成了巨大经济损失、人员伤亡，还对生态环境造成了恶劣影响。气侵早期监测是井控技术的一个重要组成部分，越早监测到气侵，侵入气体体积膨胀越少，井底压力变化越小，成功井控的概率越大。

目前，常用的气侵早期监测方法主要有3大类：平台监测法、海水段监测法和井下随钻监测法[2-3]。平台监测法操作简单方便，但精度和准确性较低，监测时间严重滞后于发生时间；井下随钻监测法弥补了常规气侵监测法结果失真和滞后的问题，但该方法信号在传播过程中会发生衰减甚至消失，同时服务成本高，不适用于高温、高压条件；海水段监测法主要包括声波监测法等，能及时监测到气侵，但平台的起伏运动会对监测设备造成干扰，特征信号识别较困难。由于深水钻井会有500～3 000 m的隔水管暴露在海水中[4]，相对于在井下使用昂贵的测量仪器，在隔水管外进行监测更加安全和高效。

多普勒超声波技术已被广泛应用于医疗成像[5-6]、无损检测[7-8]、流量测量[9-10]等领域，具有与测量流体不接触、成本低、结构简单的特点。Nguyen等[10]建立了一种基于超声波传播速度剖面的综合测量泡状流流速及含气率的方法。Abbagoni等[11]利用超声波传感器和人工神经网络进行两相流流型的识别。隋秀香、耿亚楠、李轶明等前期进行了部分超声波多普勒气侵监测实验研究[12-14]，发现侵入气体会使多普勒超声波发生衰减，因实验装置及方法的局限性、信号处理方法等问题，仅对含气率与多普勒信号的关系进行了定性描述，并没有找到它们之间的定量表征关系，且不适用于停钻不循环工况，也未考虑钻井液黏度的影响。

本文在以上研究的基础上，首先基于气液多相流理论，验证了在泥线以上、隔水管外进行气侵早期监测的可行性；然后根据多普勒超声波的传播特征，研发了气侵早期监测模拟实验平台，进行了多普勒在气、清水（蔗糖溶液）两相流中的传播实验，对信号进行了时域和频域分析，得到了多普勒信号与含气率的定量表征关系，验证了隔水管外多普勒超声波气侵早期监测方法的合理性和准确性。

1 隔水管外气侵早期监测合理性分析

气侵发生后，井筒环空中出现钻井液、岩屑、侵入气等多相流动。目前已有较多学者针对该过程进行了研究[15-17]，Sun等[17]考虑了气体的溶解与相变，建立了多组分多相流动模型，并对流型转化进行了详细描述，结果与现场数据吻合较好。因此，采用该模型进行气侵模拟。以南海某深水井为例，水深1 500 m，井深3 500 m，泵排量30 L/s，钻井液密度1.2 g/cm3，地层压力33 MPa，地层温度105 ℃。当初始含气率为1%、3%、5%时，预测的含气率随井深变化曲线如图1所示、钻井液池钻井液增量（简称钻井液池增量）随气侵时间的变化曲线如图2所示。

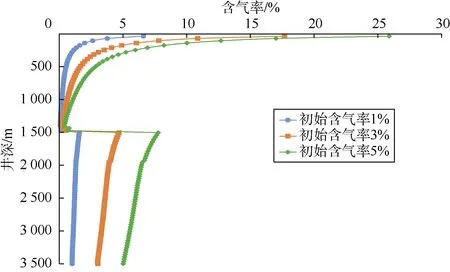
图1 含气率随井深变化曲线

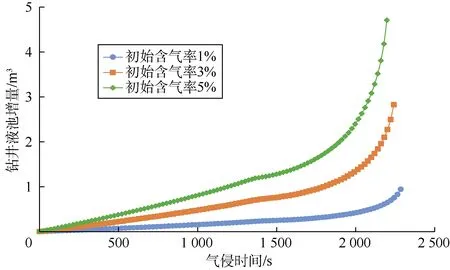
图2 钻井液池增量随气侵时间变化曲线

由图1可知当井深小于500 m时，含气率急剧增加，这时监测到气侵已难以控制，易导致井喷失控。由模拟结果及图2可知3种含气率条件下侵入气从井底到达海平面的时间分别是2 304.93，2 259.46，2 214.24 s。常规溢流监测方法中，钻井液池增量超过1 m3则报警。然而当含气率为1%时，侵入气从井底到达海平面时钻井液池增量总共不超过1 m3，该方法不适用。当含气率为3%时，侵入气运移至井深803 m处钻井液池增量为1 m3，气侵时间1 796.32 s，如果此时监测到气侵，处理时间剩余463.14 s；如果在泥线1 500 m处监测到气侵，钻井液池增量为0.73 m3，气侵时间为1 376.11 s，处理时间剩余883.35 s，比常规监测方法提前420.21 s。因此，在隔水管外进行气侵监测，发现时间更早，可供处理时间更长，控制更安全。

2 气侵早期监测模拟实验平台构建

2.1 多普勒超声波气侵监测原理

如图3所示，多普勒超声波发射器作为固定声源将超声波发射到管路中，当射入的超声波在传播过程中遇到与流体一起运动的气泡时会在其表面形成反射，接收器接收到的反射超声波频率与发射频率之间存在差异，该频率差为由流体中气泡运动而引起的多普勒频移。单个反射波的多普勒频移为：

因超声波在流体中的传播速度远大于流体流动速度，故ucosα可以省去，（1）式可以简化为：

图3 超声波多普勒法测量原理图

气液两相流体系中，气泡是多普勒信号的反射体，气泡的速度、体积和数量均为影响多普勒信号的主要因素；发生气侵时，气泡是一部分多普勒信号的反射源，使多普勒信号频率发生变化。多普勒超声波监测法正是利用这种变化对隔水管内部气体含量进行监测。当气体侵入钻井液中时，超声波发射频率和接收频率之间存在频率差，并且气体含量不同频率差也不同，从而可以对含气率进行监测。

2.2 模拟实验平台构建

基于上述原理，构建了溢流早期监测模拟实验平台（见图4），主要包括主体循环管路、液体注入与排出系统，气泡破碎装置及信号检测系统。

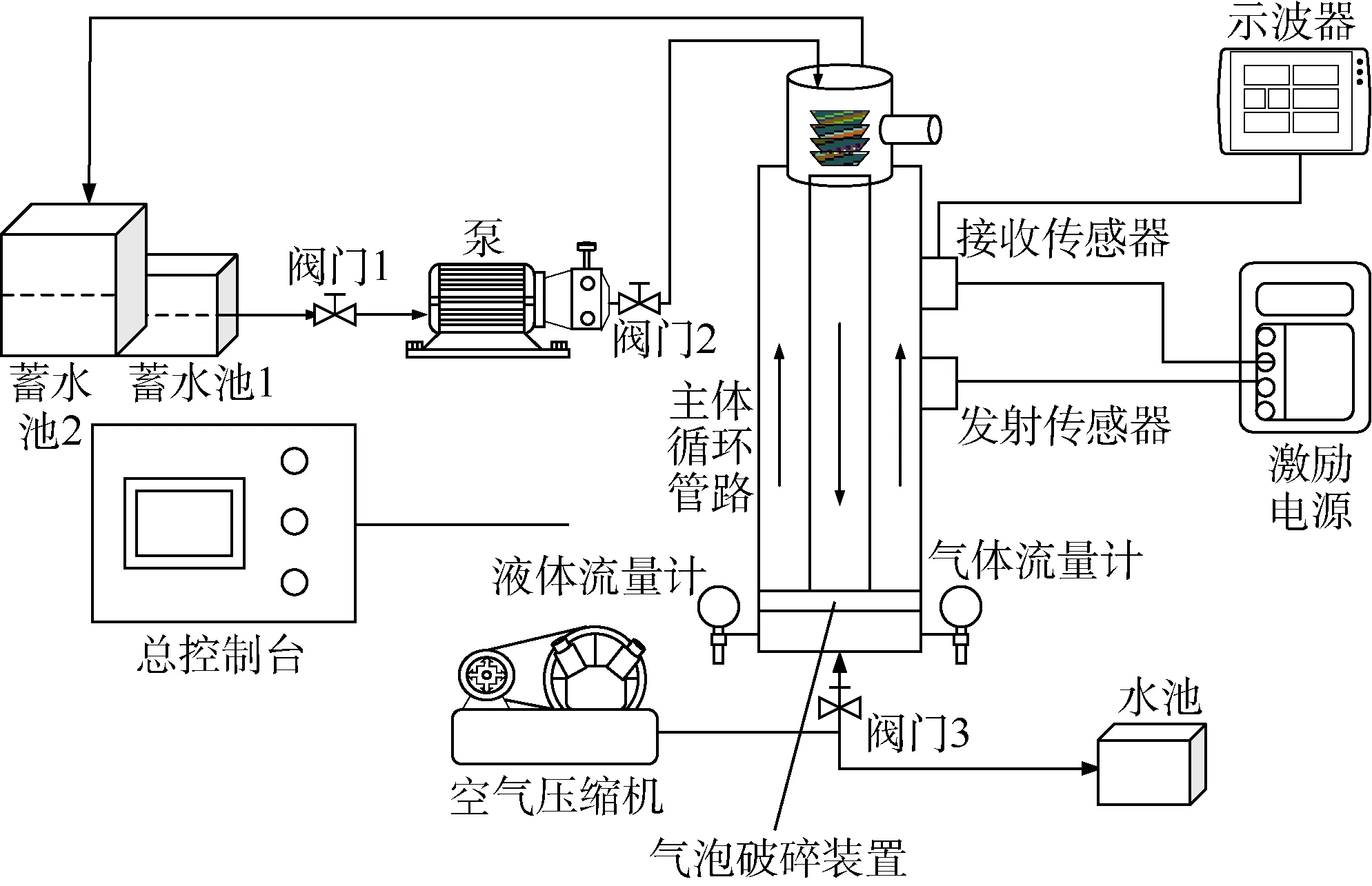
图4 实验平台装置图

该平台可用来研究多普勒超声波信号随管内流速、含气率、液体性质（如密度、黏度等）的变化规律，以及循环管内流型随含气率的变化规律。

3 气侵早期监测方法

3.1 多普勒超声波在清水-气两相流中的传播实验

在停泵和开泵状态下进行清水条件下的多普勒超声波传播实验，利用时域分析和频域分析[18]方法对获得的多普勒信号数据进行处理。

3.1.1 多普勒超声波时域信号分析

①停泵状态下的时域信号分析：在循环管中注满清水且在停泵状态下进行实验，含气率变化范围为0～46%，共获取22组不同含气率条件下的电压监测信号。选取含气率为2.4%和35.2%的信号数据，分别对0.1 s内的10 000个点在不同电压区间内的信号出现次数进行计数并作直方图（见图5）。可以看到电压幅值主要出现在-1～1 V，随含气率增加，低幅值电压区间（绝对值为0～1 V）的计数减小，高幅值电压区间（绝对值为1～2 V）的计数增加，曲线形状随含气率增加越来越扁平。

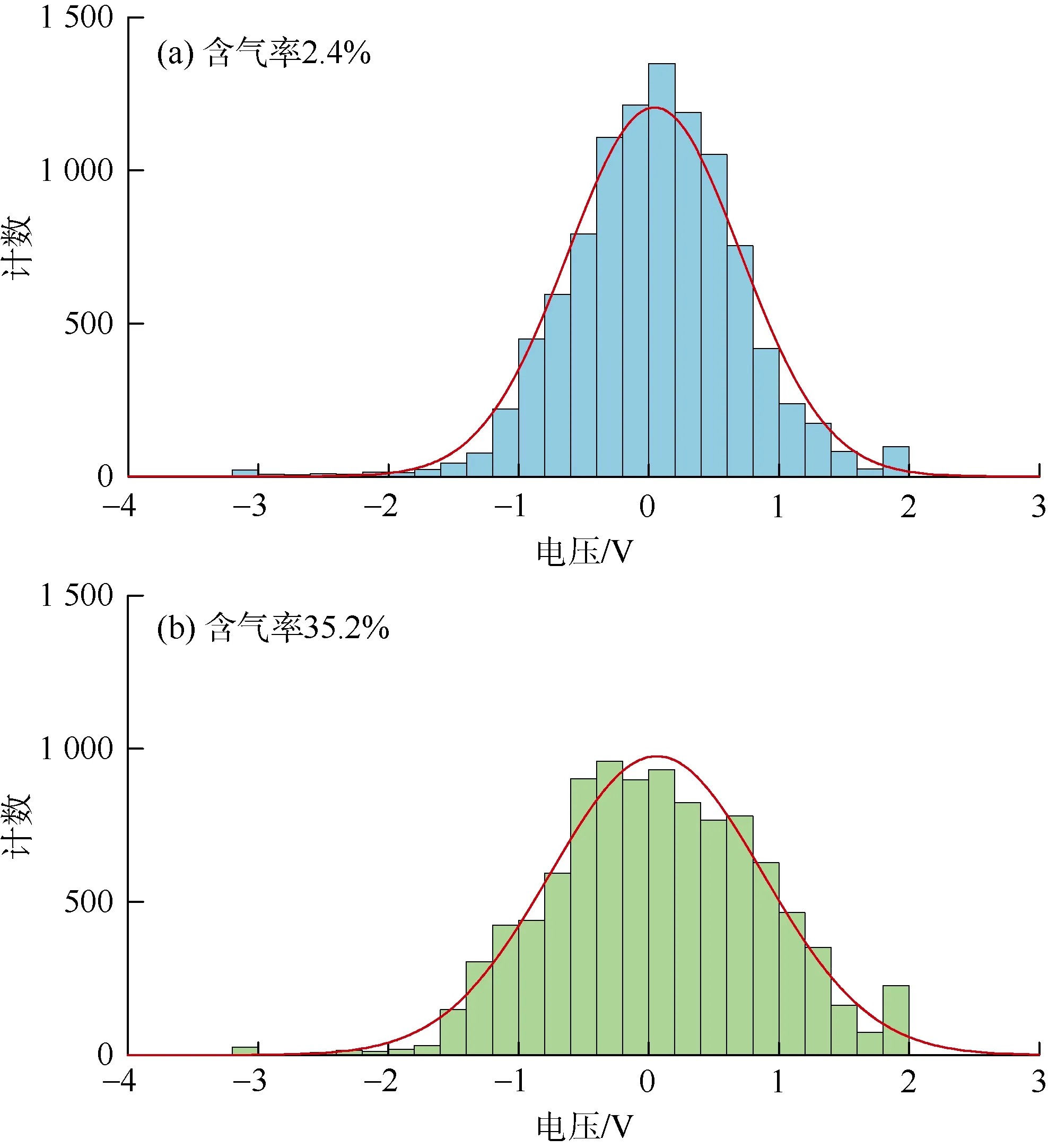
图5 不同含气率条件下各电压区间信号计数

对固定含气率条件下0.1 s内的10 000个点取信号电压绝对值的平均值，作其与含气率的关系曲线（见图6），可以看出，随含气率增加，信号电压均值先上升后下降。当含气率小于22.5%时，因多重反射对信号电压均值的增幅大于超声波的衰减程度，导致信号电压均值随着含气率的增加而增大；当含气率大于22.5%时，因气相所占体积越来越大，超声波的衰减程度大于多重反射的增幅作用，并且随着含气率增加这种趋势会不断加剧，导致信号电压均值不断减小。

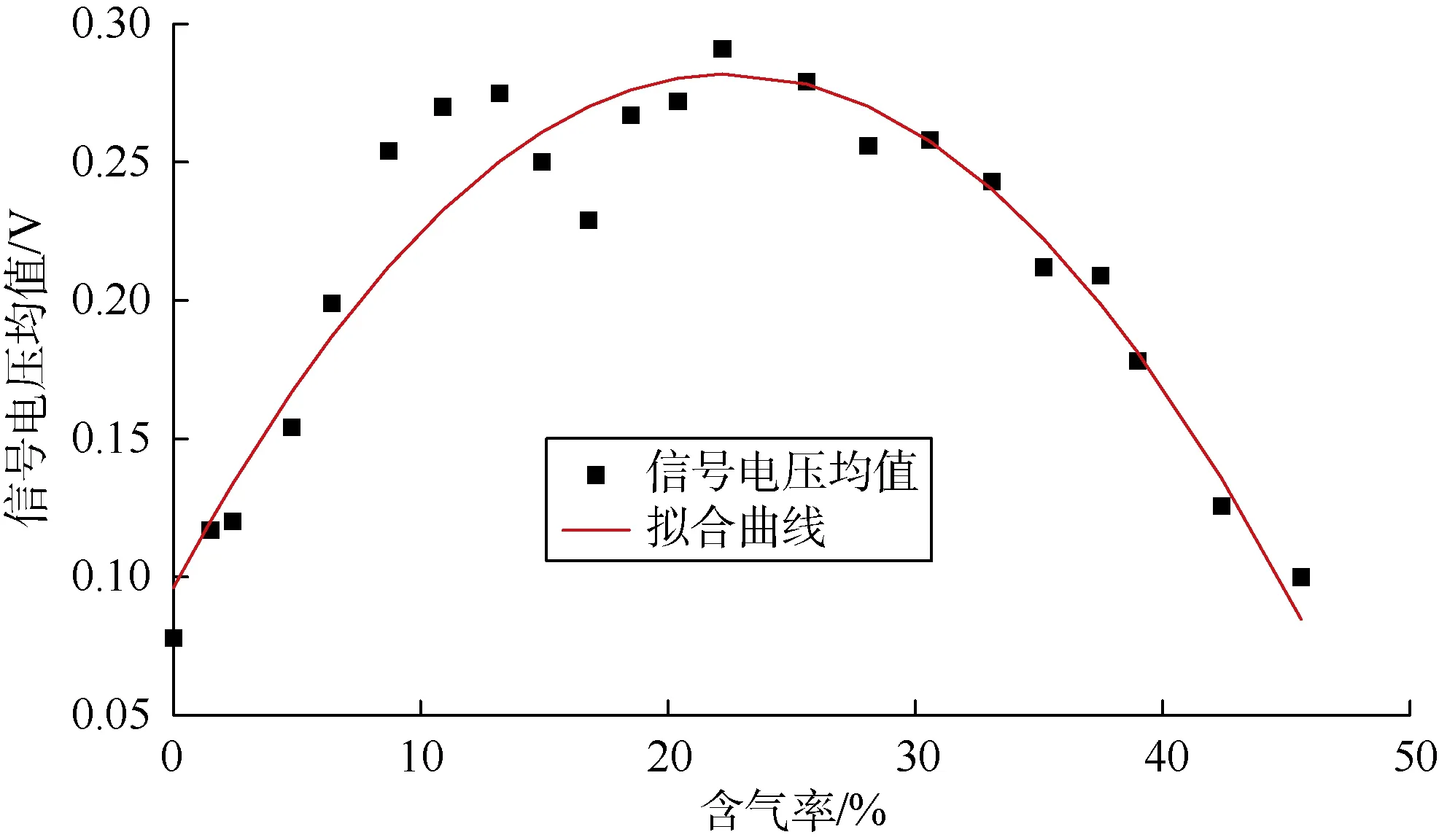
图6 停泵状态下信号电压均值随含气率的变化

拟合含气率和信号电压均值构成的散点曲线，得到二项式形式的函数表达式：

据此公式，在已知信号电压均值的情况下，可以定量反推对应含气率的近似值。

②开泵状态下的时域信号分析：开泵进行循环，管内流速分别稳定在0.40 m/s和0.65 m/s，逐渐增加管内通气量，模拟不同含气率下多普勒信号的变化，每个流速下各取22组电压监测信号。信号电压均值与含气率的关系如图7所示，信号变化与停泵时类似，随着含气率增加，信号电压均值先增大后减小。

图7 开泵状态下信号电压均值随含气率的变化

开泵时信号电压均值比不开泵时大，但变化规律基本相同。信号电压均值峰值点均出现在含气率为20%～25%，与停泵时峰值点含气率22.5%接近。拟合0.40、0.65 m/s流速下含气率和信号电压均值构成的散点曲线，得到二项式形式的函数表达式：

（3）式、（4）式和（5）式的对称轴分别为22.5%，21.0%和20.2%。可以看到，3个拟合公式形式相同，因此可以采用同一个二次函数来表达：

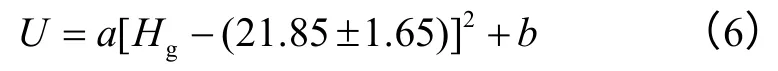
该二次函数中，对称轴为（21.85±1.65）%，a、b值与流速、信号电压强度有关。（6）式可以定量反映信号电压均值与含气率之间的对应关系。

3.1.2 多普勒超声波频域信号分析

①停泵状态下的频域信号分析：对采集到的停泵状态下的22组信号数据进行傅利叶变换，得到相应的幅度谱。由于幅值对应的纵坐标数值太小，不利于比较观察，因此对幅值进行对数变换，图8为经对数变换后的幅度谱变化曲线（含气率为0）。为探究含气率对多普勒频移的影响，需要一个参照点，图中18 000 Hz附近峰值点的横坐标是18 620 Hz，可取该区域的峰值点作为参照点，用于比较不同含气率条件下与参照点对应的频率变化。含气率为0时循环管内只有清水一种介质，超声波在传播过程中频率变化不大，接收频率与发射频率的频率差接近为0。当循环管内通入气体，超声波遇到气泡将产生多普勒频移。分析含气率为2.4%时的幅度谱可发现，其主频峰值点同样出现在18 000 Hz附近，该峰值点对应的频率是18 630 Hz。与含气率为0时对应的频率18 620 Hz相减，即为多普勒频移量，为10 Hz。

图8 含气率为0时经对数变换的幅度谱变化曲线

利用同种方法，对剩余20组不同含气率下的数据进行傅利叶变换和目标区域峰值点查找后，得到了不同含气率下的多普勒频移量，结果如图9所示，可以发现随着含气率上升，多普勒频移量增大，当含气率达到45%时，多普勒频移量已经达到150 Hz。

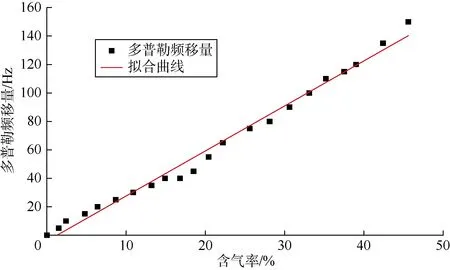
图9 停泵状态多普勒频移量随含气率的变化曲线

拟合含气率与多普勒频移量构成的散点曲线，得一次函数：

因此，也可以通过多普勒频移量来定量描述停泵不循环工况下的含气率变化。

②开泵状态下的频域信号分析：对先前采集到的开泵循环条件下的22组信号数据进行傅利叶变换和对数变换，得到相应的幅度谱（见图10）。与停泵状态下相比，开泵状态下的幅度值有了明显增大，且流速为0.65 m/s时的幅度值总体比流速为0.40 m/s时的幅度值略高，这主要是因为泵的排量取决于泵压大小，泵压越大，变频器频率越大，工作过程中产生的能量对幅度值的贡献越大。分析流速为0.40，0.65 m/s时的幅度谱，发现两种流速下，含气率为0时的主频相同，对应的频率均为16 000 Hz。

图10 开泵与关泵状态下的幅度谱对比（含气率为0）

图11为不同含气率时的频谱变化数据（含气率分别为0，10%，20%，30%和40%；流速为0.65 m/s），可以看到5组幅度谱曲线的构型基本相同，没有发生主频偏移现象，峰值点所对应的频率均为16 000 Hz，含气率的变化对峰值点无影响。流速为0.40 m/s时也呈现相同的变化规律。说明在开泵状态下，变频器工作产生的声能对幅度谱的贡献程度超过了含气率的影响。因此，无法通过该方法判断是否发生气侵。

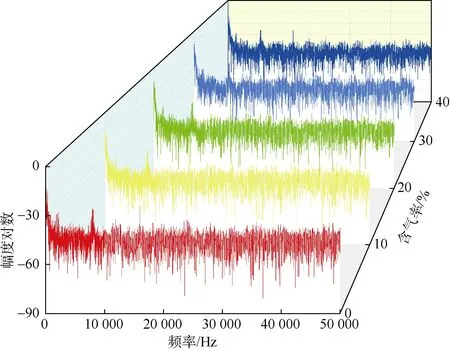
图11 溶液中含气率对幅度谱的影响（流速为0.65 m/s）

3.2 多普勒超声波在蔗糖-气两相流中的传播实验

Harker等[19]研究发现多普勒超声波的传播主要受钻井液黏度、固体颗粒等的影响。由于主体循环管下部气泡破碎装置的缝隙空间小，循环过程中固相颗粒极易堵塞装置使实验无法正常进行，因此无法模拟固相颗粒对多普勒超声波传播的影响。本实验通过增加蔗糖含量改变钻井液密度，通过加入聚丙烯酰胺（PAM）改变钻井液黏度，进而模拟密度、黏度对声波传播的影响。

在蓄液池中配制密度为1.15 g/cm3的蔗糖溶液并进行多普勒超声波传播实验，该组实验完毕，再将密度提高到1.22，1.30 g/cm3。采用布氏黏度计测试3种溶液的黏度，密度为1.15，1.22，1.30 g/cm3的蔗糖溶液黏度分别为2.5，3.6，4.8 mPa·s。

采用前述相同的时域、频域信号分析方法对蔗糖溶液停泵、开泵条件下的多普勒超声波信号进行分析。

3.2.1 多普勒超声波时域信号分析

①停泵状态下的时域信号分析：分别在不同密度、含气率（0～45%）条件下进行了23组实验。绘制含气率为20%时，4种密度溶液（清水及前述3种溶液）的信号电压随时间的变化关系图（见图12），可以发现同一含气率条件下，随溶液密度增大，信号电压幅值略微减小，说明随溶液密度增大，超声波传播时的衰减略微增大，信号电压幅值略微减小，可见溶液密度对信号的影响不大。

图12 溶液密度对多普勒信号电压的影响（含气率20%）

选取密度为1.30 g/cm3的溶液，研究黏度对多普勒信号传播的影响。向该溶液中加入PAM，使其黏度增加到35.46 mPa·s。原溶液中管内气泡体积很小，而加入PAM后管内气泡体积明显增大（见图13）。

图13 加入PAM前后蔗糖溶液中气泡大小对比（含气率18%）

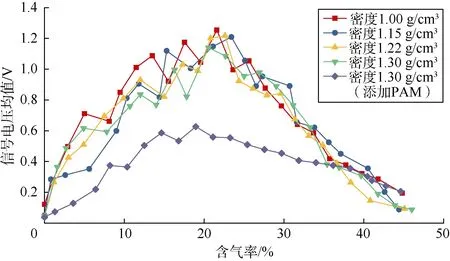
图14 不同溶液信号电压均值随含气率的变化

图14为5种溶液的信号电压均值与含气率的关系曲线，可以看到随含气率增加，信号电压均值均先上升后下降。未加PAM的4种溶液的信号电压均值在幅值上相差很小，随密度增大，信号电压均值略微减小，且均在含气率为20%～25%时出现最大值；加入PAM后，信号电压均值发生明显下降。当含气率小于20%时，由于受黏度影响，气泡多以大气泡形式向上运动，单位体积内气泡数量减小，总气液界面面积减少，超声波在气液界面处的多重反射作用减弱，因此信号电压均值小于其他4种溶液；当含气率超过20%时，管内气泡增多、气液界面面积增加，但衰减对信号电压幅值的降幅作用大于多重反射的影响，且随含气率增大，超声波衰减程度增大，信号电压均值随之减小。

拟合图14中除清水外的信号电压均值与含气率的散点曲线可得溶液在不同密度条件下的关系式。

（8）式—（11）式的对称轴值分别为21.6%，20.5%，20.9%和23.5%。可以看到拟合所得表达式均为二次函数形式，可综合表示为（6）式的形式。

②开泵状态下的时域信号分析：同样采用密度为1.22，1.30 g/cm3的蔗糖溶液及密度为1.30 g/cm3、添加PAM的蔗糖溶液共3种溶液进行实验，得到含气率变化范围为0～45%、液相流速分别为0，0.40，0.65 m/s时的信号电压随含气率变化曲线（见图15）。由图可知，随着流速增加，信号电压均值整体增大；随着含气率增加，信号电压均值先增大后减小，且3种流速下信号电压均在含气率为20%～25%时出现最大值；无气和含气率超过40%时，信号电压均值都很小；添加了PAM的蔗糖溶液因为黏度增大，在不同流速下的信号电压均值与纯蔗糖溶液相比都有一定程度的减小，且上升与下降的趋势变缓。

图15 不同密度蔗糖溶液信号电压均值随含气率的变化

拟合密度为1.30 g/cm3的两种溶液在不同流速条件下的信号电压均值与含气率的散点曲线（见图16），可以看到曲线形态与前述实验结果相同，拟合所得表达式均为二次函数形式，可综合表示为（6）式的形式。同样密度为1.22 g/cm3的溶液信号电压均值与含气率的关系拟合曲线的函数式也可用（6）式表示，说明蔗糖溶液中的气侵情况也可通过时域分析方法进行定量表征。

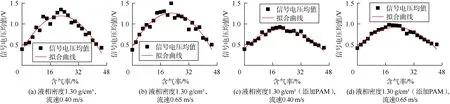
图16 不同密度、流速下蔗糖溶液信号电压均值与含气率拟合曲线

3.2.2 多普勒超声波频域信号分析

①停泵状态下的频域信号分析：在频域信号分析方法的基础上，查找含气率为0时，密度为1.00，1.15，1.22，1.30 g/cm3的溶液及密度为1.30 g/cm3、添加PAM的溶液共5种溶液的幅度谱实验数据，得到对应的5个主频频率分别为17 938，17 928，18 058，18 048，18 018 Hz，可以看到5种溶液的主频频率相差不大。进一步统计不同含气率条件下的多普勒频移量，得到多普勒频移量随含气率的变化关系曲线（见图17）。图中显示多普勒频移量随着含气率的增大而增大，未加PAM的溶液多普勒频移量曲线大部分重合在一起，基本呈相同的线性关系；而加入PAM溶液的多普勒频移量曲线上升趋势变缓，幅值在相同含气率下明显下降，但依然基本呈线性关系。因此，蔗糖溶液停泵状态下同样可以用频域信号分析的方法对含气率进行定量表征。

图17 蔗糖溶液多普勒频移量与含气率拟合曲线

②开泵状态下的频域信号分析：图18为流速0.65 m/s，含气率为0时，5种溶液的幅度谱与信号频率的关系曲线。可以发现，5条幅度谱曲线构型基本相同，仅在幅值上有细微差别，且均在15 000 Hz附近存在主频，经查找实验数据主频频率均为16 000 Hz，且含气率对多普勒频移基本无影响。当流速为0.4 m/s时，所得结果基本与此相同。这说明开泵状态下，溶液性质改变不会对主频频率产生影响；与停泵状态下的实验结果进行对比可知，变频器工作产生的声能对幅度谱幅度值的贡献程度超过了含气率的影响，主频频率不再随含气率的增大而产生偏移。因此，蔗糖溶液开泵条件下，不能通过频域信号分析方法进行含气率的定量表征。

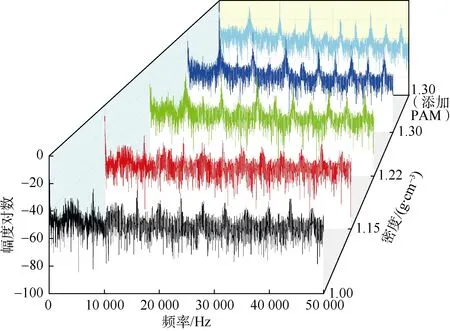
图18 溶液密度（黏度）对幅度谱的影响（含气率为0）

基于上述分析，可以将隔水管外多普勒超声波气侵早期监测方法归纳为：①在隔水管外沿程安装多普勒发射及接收模块，由发射模块发出多普勒超声波信号，经隔水管壁穿透到钻井液中，由接收模块接收信号；②平台上的信号采集及分析系统对接收到的信号进行初步分析，如果与发出信号波形一致，则无气侵发生，如果信号波形发生变化，则进行时域、频域信号分析；③根据时域、频域分析法建立的多普勒信号与含气率的关系式，定量求出含气率的值，从而指导下一步的压井作业。

4 结论

无论开泵循环或停泵，深水钻井隔水管外多普勒超声波信号电压均值均随着含气率上升先上升后下降，并与含气率具有二次函数关系，采用监测信号电压均值可定量反推对应含气率的近似值；多普勒超声波信号在黏度较大的溶液中幅值明显减小且变化趋势变缓，黏度的影响远大于密度。

停泵状态下多普勒频移量随含气率的增大而增大，二者基本呈线性关系，采用监测多普勒频移量可定量描述含气率的变化；开泵循环状态下变频器产生的声能对幅度谱的影响超过了含气率，频域信号分析不能判断是否发生气侵。

隔水管外多普勒超声波法气侵早期监测为非接触式测量手段，不直接接触流体、不受钻井工况影响，可根据多普勒超声波信号的变化对含气率进行定量表征，实现深水钻井气侵的早期监测。

符号注释：

a，b——拟合常数；c——超声波在流体中的传播速度，m；f1——发射传感器发射的超声波频率，Hz；f2——流体中气泡接收到的超声波频率，Hz；f3——接收传感器接收到的超声波频率，Hz；Hg——含气率，%；u——流体流动速度，m/s；U——多普勒超声波信号电压均值，V；α——超声波入射角度，（°）；Δf——多普勒频移量，Hz。