PVA-ECC徐变性能试验研究

王玉清, 刘 潇, 刘曙光, 孙 亮

(1.内蒙古工业大学 土木工程学院, 内蒙古 呼和浩特 010051; 2.内蒙古工业大学 矿业学院, 内蒙古呼和浩特 010051; 3.国网内蒙古东部电力有限公司兴安供电公司, 内蒙古 乌兰浩特 137400)

在持续恒定荷载作用下,水泥基材料的变形随时间延长而不断增长的现象称为徐变.徐变是水泥基材料的重要特性,一般徐变变形比瞬时弹性变形大1～3倍.徐变的存在会引起预应力混凝土结构的预应力损失,使结构构件的变形增加,在构件中引起应力重分布等,对结构构件在长期荷载作用下的开裂、变形等性能有较大影响.1907年,Hatt[1]发现了混凝土材料在应力不增加的情况下变形会缓慢增长的现象,并称之为徐变.同年,美国材料试验学会(ASTM)首先报道了钢筋混凝土梁的徐变.1917年,Smith[2]在美国混凝土学会(ACI)杂志上发表了混凝土徐变与徐变恢复的试验结果.直到1931年,Davis等[3]对混凝土徐变性能进行了系统研究之后,大家才对混凝土的徐变性能有了较为明确的认识.100多年来,国内外学者对混凝土徐变进行了大量的研究,并取得一些成果[4-7].一般认为水泥基材料徐变的产生与其中胶凝体、水分的迁移等有关;影响水泥基材料徐变的因素较多,主要有原材料的性质及其含量、加荷龄期、加荷应力比、持荷时间、养护条件、环境相对温湿度和几何尺寸等[8-14].但是到目前为止,对混凝土等水泥基材料徐变机理的认识尚不够深入,理论也不够完善.

同时,随着人们对结构功能和材料性能要求的不断提高,近年来对改性水泥基材料的研究与应用日益增多,纤维水泥基材料越来越得到重视,聚乙烯醇纤维增强水泥基复合材料(engineered cementitious composite with polyvinyl alcohol fiber,PVA-ECC)便是其中之一.聚乙烯醇(PVA)纤维具有高强、高弹性模量、耐酸、耐碱等优点,且与聚乙烯(PE)等纤维相比,价格更加低廉.将其添加到水泥基材料中,可以大大改善基材性质,提高基材的抗裂、抗渗、抗冲击韧性及耐久、耐高温、耐腐蚀等性能,故近年来受到工程界人士的关注,成为工程材料研究的热点之一[15-17].但目前国内外学者对于PVA-ECC材料短期力学性能的研究较多,对其长期性能的研究主要集中在耐久性、侵蚀等方面,而对PVA-ECC材料徐变性能的研究尚少.在现有的研究成果中,Boshoff等[18-19]、Kong等[20]将PVA-ECC假定为一种均质材料,并进行了拉伸荷载作用下的徐变性能研究,提出了PVA-ECC拉伸徐变模型;Benny等[21]根据PVA-ECC材料短期力学性能预测了高拉应力下的徐变;张为民等[22]对PVA纤维增强水泥基复合材料的轴压徐变性能进行了研究,得出了纤维掺量大于1%时,徐变系数随纤维掺量的变化规律.另外,部分学者研究了纤维混凝土的徐变性能,如于俊超[23]研究了加入不同种类纤维混凝土的徐变性能,得出了纤维混凝土试件徐变度随龄期的变化关系;何智海等[24-25]研究总结了2种PVA纤维掺量及减缩剂对高强混凝土徐变性能的影响规律,发现在所研究纤维掺量范围内,PVA纤维的掺入提高了混凝土的徐变系数,掺用过量的纤维显著增大了材料的徐变系数.在以上研究中,所考虑工况比较单一,研究不够深入,成果也不够丰富.除此之外,未见到其他公开发表的关于PVA-ECC徐变性能的研究文献.而PVA-ECC结构构件的长期力学性能分析、裂缝及变形计算、预应力损失计算、非线性有限元分析等又需要以材料徐变性能的研究结果为基础[26-27].因此,PVA-ECC材料徐变性能研究成果的匮乏阻碍了PVA-ECC材料后续其他性能的研究及工程应用.

基于上述情况,本文对7组不同纤维掺量和加荷龄期下的PVA-ECC试件进行了恒定轴压作用下的徐变试验研究,结合国内外对水泥基材料徐变性能的研究理论与计算方法,确定了能够反映PVA-ECC材料徐变性能的评价指标,并根据试验结果提出了徐变评价指标的估算模型.以期为PVA-ECC构件的徐变计算及构件设计方法的制定提供参考,从而促进PVA-ECC材料的工程应用.

1 试验概况

1.1 试验设计

本试验参照GB/T 50082—2009《普通混凝土长期性能和耐久性能试验方法标准》,共设计7组PVA-ECC试件.由于无粗骨料,按照砂浆徐变试验的尺寸要求,确定采用尺寸为40mm×40mm×160mm的棱柱体试件,每组试件分为徐变和收缩2类,每类试件各2个且每组试件均为同一批次制作,收缩试件作为对比试件以得到徐变试件在同一时期的收缩值.试验加载应力水平均为0.4fc,其中fc是尺寸为40mm×40mm×160mm的棱柱体试件28d抗压强度.PVA-ECC材料配合比为m(水泥)∶m(粉煤灰)∶m(标准砂)∶m(水)∶m(增稠剂)∶m(消泡剂)∶m(增塑剂)∶=600∶400∶600∶260∶1∶2∶20,纤维掺量(体积分数,以PVA-ECC材料总体积计)为0%、1.0%、1.5%、2.0%.纤维采用日本Kuraray公司生产的REC15型PVA纤维,其性能参数见表1.

表1 PVA纤维性能

1.2 加载方案及数据采集

所有试件均在标准养护室中养护至7d龄期后移入徐变试验环境,收缩试件与徐变试件始终放置于同一环境中.试件在实验室放置到14、28、90、180d 时进行加载,在对徐变试件加载的过程中,收缩试件自然搁置于台面,下垫塑料布,以避免试件下部与台面进行水分交换.徐变试验环境为实验室常温环境,加载装置如图1所示,加载通过机械千斤顶在试件底部持力.加载设备采用天津多维克贸易有限公司生产的20t机械千斤顶,力值监控采用力传感器连接测力仪进行,其中传感器采用广州电测生产的轮辐式yzc-219传感器,测力仪采用WTB2116C多通道测力仪,试验加载程序参照GB/T 50152—2012《混凝土结构试验方法标准》执行.试验中涉及徐变及收缩的变形均采用电测法粘贴应变片进行测量,在试件的1对平行侧面中部贴纵向应变片,以量测试件的纵向变形,在试件另一对平行侧面中部贴横向应变片,以量测试件的横向变形,任何一个方向的应变取2个应变值的平均值,2个方向的应变片长度均为20mm.采用江苏东华公司生产的DH3816静态电阻应变仪采集应变数据并记录保存.

图1 加载装置示意图Fig.1 Diagram of loading equipment

1.3 试验工况

本文针对PVA纤维掺量、加荷龄期各影响因素进行工况设计,如表2所示.表中F0-28-270表示纤维掺量为0,加荷龄期为28d,持荷时间为270d,其余以此类推.PVA-ECC材料28d力学性能见表3,表中E为弹性模量,μ为泊松比.每组试件应变采集的持荷时间点定为1、3、7、14、28、45、60、90、120、150、180、270d,试验加载应力水平均为0.4fc.采用电测法以每1h采集1次的频率对试件变形进行连续采集,最后根据持荷时间节点统计试件的徐变值.

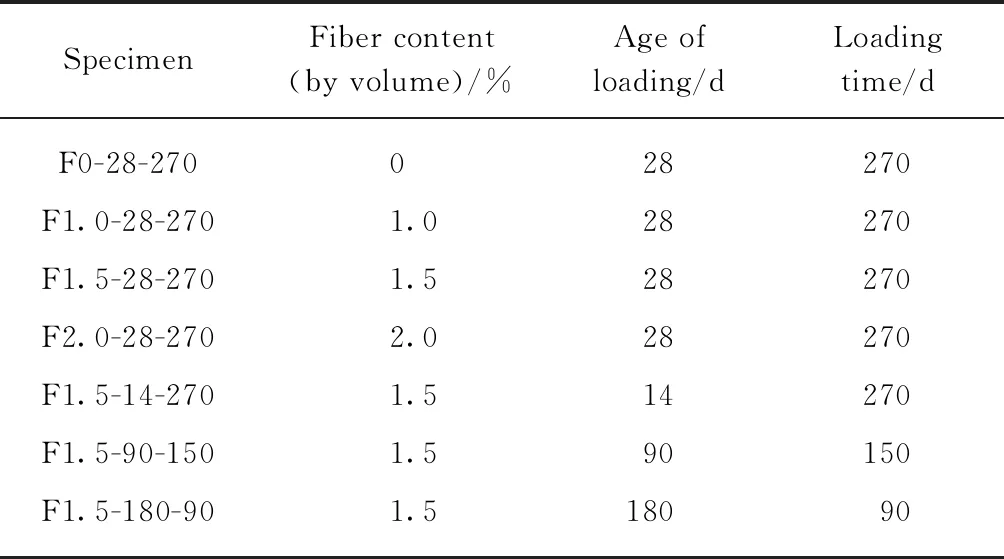
表2 试验工况

表3 PVA-ECC力学性能

2 徐变性能分析

PVA-ECC的徐变应变可由轴向总变形减去其加荷后的瞬时轴向变形以及相应对比试件的轴向收缩变形得到；徐变系数为单位弹性瞬时应变下的徐变应变,可由徐变应变除以弹性瞬时应变计算而得,如式(1)所示:

φ(t,t0)=εc(t,t0)/ε0

(1)

式中：φ(t,t0)为试件在龄期t0(d)加荷,t(d)时刻的徐变系数;εc(t,t0)为试件的受压徐变应变,μm/m;ε0为加载至应力σ(MPa)时试件的瞬时轴向应变,其值为加载后数据稳定时所读轴向受压应变值，μm/m.

图2～5为各工况下PVA-ECC材料徐变应变- 持荷时间与徐变系数-持荷时间曲线.图2～5显示：徐变发展的整个过程大致经历了3个阶段,在徐变初期,各组试件的徐变值相差较小,曲线几乎重合,徐变系数呈近似线性增长,且曲线斜率较大,说明加载初期PVA-ECC材料徐变增长迅速,将这一阶段称为徐变快速增长阶段；随着持荷时间的延长,各工况的曲线逐渐分离,且徐变增长速率均开始下降,徐变应变与徐变系数曲线逐渐偏向横轴,将此阶段称为徐变第2发展阶段；之后徐变增长趋于平缓,徐变应变与徐变系数曲线开始收敛,曲线斜率大大降低,将此阶段称为徐变收敛阶段.总结徐变随持荷时间的变化特征,可将之概况为：前期快,后期慢,持荷约60d时徐变的大部分基本完成.将PVA-ECC材料与混凝土的徐变-时间关系进行比较,发现混凝土的徐变终值普遍较小,且其徐变系数-时间关系曲线普遍具有第1阶段较短且曲线斜率较小,第2阶段曲线较平缓、持续时间长,第3阶段曲线斜率稍大,收敛较慢的特征.这说明，与混凝土相比,PVA-ECC材料早期徐变发展速率较快,徐变发生量较大;中晚期收敛较快,徐变发生量较小[28-34].下文将围绕以上3个阶段,对本试验各工况下PVA-ECC材料的徐变性能进行讨论.

图2 不同纤维掺量下PVA-ECC徐变应变随持荷时间变化曲线Fig.2 Variations of creep strain with loading time of PVA-ECC under different fiber contents

图4 不同加荷龄期下PVA-ECC徐变应变随持荷时间变化曲线Fig.4 Variations of creep strain with loading time of PVA-ECC under different age of loading

图5 不同加荷龄期下PVA-ECC徐变系数随持荷时间变化曲线Fig.5 Variations of creep coefficient with loading time of PVA-ECC under different age of loading

2.1 PVA纤维掺量的影响

由图2、3可见：PVA-ECC的徐变应变和徐变系数随持荷时间变化曲线的走势及发展规律基本一致,在纤维掺量范围内(0%～2.0%),PVA纤维降低了基材抵抗徐变的能力,使试件的徐变增加;纤维掺量越高,材料的徐变越大,纤维掺量为1.0%、1.5%、2.0%的试件在持荷时间为60d时的徐变应变和徐变系数分别是纤维掺量为0%的1.13、1.44倍，1.42、1.09倍，1.56、1.55倍；各组试件在60d时的大部分徐变已发生,纤维掺量为0%、1.0%、1.5%、2.0%的试件在60d时的徐变系数是270d的82%、80%、93%、91%,且纤维掺量越大,60d内发生的徐变占总量的比例越大；随着持荷时间的进一步延长,60d后徐变增长速度大大降低,曲线趋于平缓,270d 时纤维掺量为1.0%、1.5%、2.0%的试件的徐变应变和徐变系数分别是纤维掺量为0%的1.15、1.27倍，1.29、1.12倍，1.38、1.40倍.由图2、3还可见：各组试件在第1阶段的徐变速率相差极小,曲线几乎重合,但从第2阶段开始,掺纤维试件的徐变增长速率明显高于基材的徐变增长速率,且纤维掺量越高,试件的徐变增长速度越快.产生这一现象的原因是PVA纤维加入水泥基后,水泥基材与纤维2种材料的界面难以紧密结合,在水泥结硬过程中产生初始微裂缝;加之PVA纤维掺量较大时,纤维容易结团、难以分散均匀,使得材料内部出现较多原始缺陷,降低了材料的密实性,在荷载作用下材料的变形增加.同时,初始微裂缝和缺陷在加荷初期发展不充分,故4组试件在第1阶段的变形差距甚微;但随着荷载的增加,初始微裂缝和缺陷的发展越来越充分,且PVA纤维掺量越大,微裂缝和缺陷越多,材料的变形速率也越大,故曲线在第2阶段出现分离.另外,纤维掺量在1.5%和2.0%时试件的徐变始终相差较小,2种纤维掺量下的2条曲线基本重合,且与F1.0-28-270试件的曲线相差较大,说明纤维掺量较高时,纤维掺量变化对试件徐变性能的影响程度变化不大,且结合材料基本力学性能的研究成果[35],说明PVA纤维掺量达到2.0%以后,再提高纤维掺量,PVA-ECC的各项性能均有所下降,且经济性降低,故在PVA-ECC的实际工程应用中,纤维掺量不宜过大.

2.2 加荷龄期的影响

由图4、5可以看出,在加荷龄期范围内(14～180d),在同一持荷时间下徐变应变随加荷龄期的推迟而减小,即加荷龄期越早,同一持荷时间内发生的徐变越大,此特征与混凝土材料的徐变特性相似.同时,180d加荷龄期时进行加载的试件,徐变系数曲线较徐变应变曲线斜率更大,而其他加荷龄期的试件2类曲线斜率相近,说明随加荷龄期的推迟,材料的瞬时弹性变形减小.这是因为加荷龄期较早的试件材料成分中水泥水化反应程度不充分,弹性模量偏低,加载后短期内产生较大变形,使瞬时弹性变形量增加;加荷龄期较晚的试件在加载时基材中水泥的水化反应相对进行得较充分,更多的水泥胶凝体向结晶体转化,基材的弹性模量提高,材料抵抗变形的能力较高,加载后瞬时弹性变形量减小,故同一持荷时间下材料徐变系数提高.另外,与纤维组不同的是,本组试验中徐变应变曲线与徐变系数曲线从加荷初期便有一定分离,说明在加荷初期,加荷龄期对试件徐变的影响程度大于纤维掺量的影响.

以28d加荷龄期为对照组,14、90、180d加荷龄期各试件与28d加荷龄期试件的徐变比例关系,如图6所示.

图6 不同加荷龄期下PVA-ECC相对徐变随持荷时间变化曲线Fig.6 Variations of relative creep with age of loading of PVA-ECC under different age of loading

通过图6可知,在90d持荷时间内,不同加荷龄期下的徐变相对28d加荷龄期的徐变比值并不是一定值,加荷龄期越早的试件,加荷初期徐变相对比值越大,说明在加载初期徐变增长速度越快;60d 后徐变增长速度基本趋于一致,相对值稳定在某一定值左右,稳定后14、90、180d加荷龄期与28d 加荷龄期的相对徐变比值约为1.2、0.7和0.4.

3 PVA-ECC徐变的估算

为了能够获得普遍适用的徐变计算方法,研究人员提出了较多徐变估算模型.目前国际上对混凝土徐变性能的研究较为成熟,常用的混凝土徐变计算模型有ACI 209R-92模型[36]、CEB-FIP90模型[37]、B3模型[38]和GL2000模型[39].JTG D62—2004《公路钢筋混凝土与预应力桥涵设计规范》,借鉴了CEB-FIP90模型方法来计算混凝土的徐变系数.而关于PVA-ECC徐变计算模型的研究较少,尚未形成成熟的计算理论.因此本文拟在试验研究的基础上,以徐变系数为指标,总结PVA-ECC的徐变发展规律,在已有混凝土徐变计算模型的基础上，通过与本试验数据进行对比,对现有的徐变计算模型进行修正与改进,从而得到更符合PVA-ECC的徐变估算模型.下面将着重针对使用较多的ACI 209R-92和CEB-FIP902种模型与本试验结果进行对比分析.

ACI 209R-92模型可由式(2)表示：

(2)

可以看出徐变系数由持荷时间参数βc(t-t0)与徐变修正系数γcr这2部分组成,其中γcr考虑了加荷龄期、环境相对湿度、混凝土构件平均厚度、混凝土稠度、骨料含量及混凝土中所含空气体积等因素的影响[38].

CEB-FIP90模型可由式(3)～(5)表示：

φ(t,t0)=φ0βc(t-t0)

(3)

φ0=φRHβ(fcm)β(t0)

(4)

(5)

式中：φ0为各义徐变系数；β(fcm)为混凝土强度修正系数；β(t0)为加载龄期修正系数.

可以看出徐变系数由βc(t-t0)和φ0这2部分组成,其中名义徐变系数φ0考虑了加荷龄期、环境相对湿度、混凝土强度、混凝土构件体表比等因素的影响[37].

通过式(2)～(5)可以看出,ACI 209R-92和CEB-FIP90这2种模型都是由持荷时间参数乘以各因素对徐变的影响系数.本文在建立PVA-ECC徐变估算模型时,参考已有混凝土材料徐变计算模型的建立方法,拟采取如下路线进行研究：先排除其他因素对徐变的影响,只考虑持荷时间的影响,得出持荷时间参数βc(t-t0),在此基础上再考虑各相关因素的影响,乘以各因素的徐变影响系数,得到各工况下PVA-ECC的徐变估算模型.

由试验结果可知,PVA-ECC材料的徐变前期发展较快,后期发展速度逐步减小，最后趋于收敛,经历了明显的3个发展阶段.为了更好地反映PVA-ECC材料徐变随持荷时间的变化特点,在确定徐变估算模型时,本文拟将徐变随时间发展的函数以分段函数的形式表示.通过对本文试验数据进行拟合,排除其他因素的影响,得到了PVA-ECC材料的持荷时间参数表达式(模型Ⅰ),如式(6)所示：

(6)

计算在持荷时间为5～14d及45～60d之间的徐变时采用线性内插法.

另外,将式(6)确定的曲线与ACI209R-92和CEB-FIP90模型的持荷时间参数曲线绘于图7.由图7可见,在持荷约45d之前时,由式(6)确定的模型曲线与ACI209R-92模型曲线非常接近,但在后期,ACI209R-92模型曲线收敛较慢,二者相差较大;在持荷约60d之后,由式(6)确定的模型曲线与CEB-FIP90模型曲线虽数值相差较大,但斜率非常接近,2条曲线几乎平行.由此,本文提出PVA-ECC材料徐变估算的第2种计算方法：将ACI209R-92和CEB-FIP90模型中各自能较好反映PVA-ECC材料徐变发展趋势的曲线段进行组合,形成PVA-ECC材料的徐变计算模型(模型Ⅱ),即持荷45d之前采用ACI209R-92模型计算,持荷60d之后采用CEB-FIP90模型计算值加常数项进行计算,经与本试验数据进行对比分析,建议取常数项为0.60.模型Ⅱ计算式如式(7)所示：

(7)

图7 各模型下持荷时间参数曲线关系Fig.7 Curve relation of loading time parameter of different models

计算持荷时间为45～60d期间的徐变时采用线性内插法.

将模型Ⅰ、模型Ⅱ确定的持荷时间参数曲线与由本文试验数据确定的曲线统一绘于图8.由图8可知：模型Ⅰ的计算结果在整个徐变发展过程中与试验结果吻合程度较高;模型Ⅱ在计算前期徐变时与试验结果吻合较好,计算稳定后的持荷时间参数时计算结果略大于模型Ⅰ,但由于模型Ⅱ前2个阶段的徐变函数由1个公式表达,故其计算相对较简便.

图8 式(6)、(7)与试验数据对比关系Fig.8 Comparisons between equation (6), equation (7) and experimental data

在此基础上进一步考虑纤维掺量与加荷龄期的影响,在式(6)、(7)的基础上乘以影响系数,得到关于PVA-ECC徐变系数φ(t,t0)的计算式：

φ(t,t0)=kf·kd·βc(t-t0)

(8)

其中，

(9)

kd=1.622-0.012t0+0.00004t02

(10)

式中：kf为PVA纤维体积掺量修正系数;kd为加荷龄期修正系数;Vf为PVA纤维掺量,纤维掺量大于1.5%时按照1.5%取值.

通过式(8)～(10)计算出的PVA-ECC受压徐变系数计算值与试验值的比值见表4,除个别点外,计算值与试验值吻合度较高.通过与试验数据进行比较,由模型Ⅰ与模型Ⅱ建立的PVA-ECC材料徐变估算公式计算值与试验值的比值均值为1.09、1.18,方差为0.04、0.07,误差满足工程精度要求,且相对于模型Ⅱ,模型Ⅰ具有更高的精度.

表4 PVA-ECC徐变系数计算值与试验值的比值

4 结论

(1)与混凝土徐变发展过程类似,PVA-ECC的徐变发展也呈现出前期快、后期慢,最后逐渐趋于稳定的变化规律.

(2)在设计工况条件下,PVA-ECC材料的徐变应变和徐变系数随纤维掺量的增加而增大,随加荷龄期的延长而减小.

(3)结合已有的混凝土徐变预测模型和本文试验结果,提出PVA-ECC材料徐变估算的2种模型,且2种模型的计算值与试验值均具有较好的吻合度,误差满足工程精度要求.模型Ⅰ的计算结果比模型Ⅱ具有更高的精度,但模型Ⅱ的计算过程相对简便.本文提出的徐变估算模型可为今后PVA-ECC结构构件在长期荷载作用下的徐变计算及变形验算等提供参考依据.