基于PCA的桥梁静态监测数据频域分析方法

唐 浩， 梁 杨， 余 建

(1.招商局重庆交通科研设计院有限公司， 重庆 400067；2.重庆市市政设施运行保障中心， 重庆 400015)

近年来，由于结构老化、车辆超载、船撞、自然灾害等影响因素导致桥梁安全问题频出[1-5]。2000年以来，许多桥梁都陆续建立了远程实时监测系统[6-9]，技术人员通过对实时监测数据的综合分析，以确保桥梁的安全运营[10-15]。面对海量监测数据，本文提出一种基于PCA的桥梁静态监测数据频域分析方法，通过分析时间序列信号在频域中的分布特征，有效去除或减小活荷载效应、短时温差(日温差及骤变温差)效应以及随机干扰误差的影响，提高信噪比，利用PCA得到的主分量信息构建频域评价指标，进而更加准确地描述桥梁结构运营状态，为在役桥梁的管养提供科学参考依据。

1 桥梁监测信号频域分析

在桥梁长期运营监测中，实测得到的结构响应信号R是桥梁在各种作用下的综合响应，可表述为：

R=F(t,T,D,L,S,O)

(1)

式中：F(·)为函数关系；t为时间作用；T为温度作用；D为结构恒载作用；L为活荷载作用；S为测试误差作用；O为其它作用。

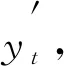
y0=xT0+xD+ε0

(2)

y1=xT1+xD+xL1+ε1

(3)

式中：y0、y1分别为初始化t0时刻和其它t1时刻传感器采集到的绝对响应；xT0、xT1分别为初始化t0时刻和其它t1时刻温度荷载响应；xD为结构恒载响应；xL1为活荷载响应；ε为测试误差及其它综合作用。

一般情况下，选择桥上无通行车辆时刻作为初始化时刻，近似忽略活荷载影响。因此，当结构恒载未发生改变时，t1时刻响应信号相对值为：

(4)

若结构恒载发生改变，则t2时刻响应信号相对值为：

y2=xT2+(xD+ΔxD2)+xL2+ε2

(5)

(6)

式中：ΔxD2为t2时刻结构恒载变化量。

由上可见，采集到的桥梁结构监测信号主要成分如式(6)，当ΔxD2=0，式(6)变为式(4)。实际工程应用中，以上信号在时间域内很难直接分离，本文通过快速傅里叶变换FFT(Fast Fourier Transform)将桥梁结构综合响应转换为频域信息，实现了各种信号在频域内的有效分离。

对于离散的数字信号进行傅里叶变换，需借助离散傅里叶变换公式DFT(Discrete Fourier Transform)：

(7)

WN=e-j2π/N

(8)

式中：N为序列点数；n为频域离散值的序号；k为时域离散值的序号。

1965年美国学者Cooley和Tukey提出了傅里叶变换快速算法FFT，其基本思想是把整个数据序列{xk}按奇、偶分成2个较短的序列分别进行变换，然后再把它们合并起来，得到整个序列{xk}的离散傅里叶变换。

2 多组分信号频域分离

以下分析研究中，将时间尺度h近似为s，则每隔1 h采样的静态监测数据采样率为1 Hz。公式(6)中，ε2-ε0表示测试误差及其它综合效应影响，其作用的时间尺度很广，可认为在信号幅值谱的各个频带均有分布。xL2表示活荷载效应影响，其变化可以用min作为度量尺度，即特征频带范围集中在60 Hz附近，由于桥梁静态监测数据采样率为1 Hz，不满足采样定理，活荷载效应会产生频谱混叠现象。但是，本文所分析的静态监测数据实际是每隔10 min采样得到的监测数据预处理后的信号。提取中值的预处理方式一定程度上已经大大消除或减弱了活荷载效应的影响。ΔxD2表示结构恒载变化的影响，不会出现周期“波动”现象，可认为在信号幅值谱接近0频率的低频带有分布。xT2-xT0表示温度作用的影响，包含日温差影响、骤变温差影响以及年温差影响。其中，日温差变化的时间尺度最短，以d为度量尺度，具有周期性；骤变温差的时间尺度较短，一般在几d内完成，其出现及持续的时间具有随机性；年温差主要随一年四季更替而发生变化，以年为度量尺度，也具有周期性。

对于年温差效应，重现周期为1年，约8 760 h，故频率为0.000 141 Hz；对于日温差效应，每隔24 h变动1次，故频率为0.041 67 Hz；对于骤变温差效应，在1年中通常发生多次，且每次骤变过程往往需要从数d至1月左右的时间，故频率分布介于年温差效应和日温差效应之间。图1、图2分别是自2014年3月27日至2016年1月22日国内某实桥D1-1测点温度、挠度监测数据的时域、频域图。从图1(b)和图2(b)幅值谱中可以看到，温度和挠度信号均在0.041 68 Hz处有一个明显的幅值集中，该频率与前述理论分析的日温差效应频率基本一致。

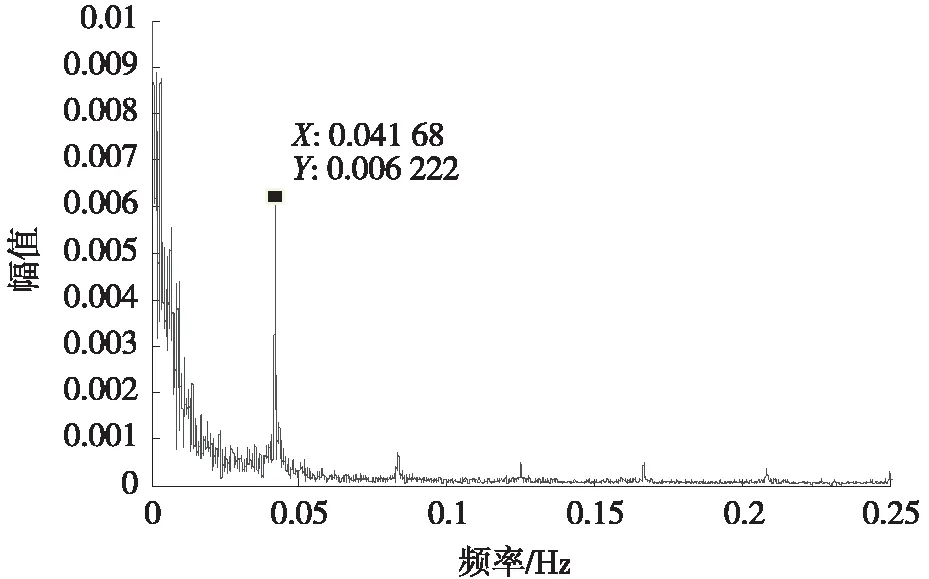
(b) 挠度幅值谱

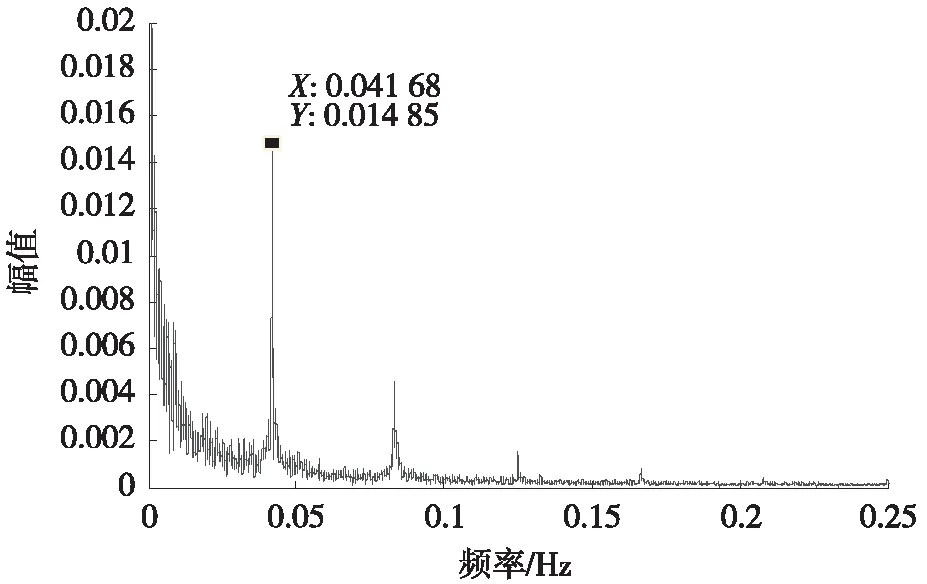
(b) 温度幅值谱

通过以上分析可将桥梁结构时域信号按照不同组分在频域内有效区分开来，如表1所示，保留低频段幅值信息并采用PCA提取主分量信息构建桥梁结构监测数据频域评价指标。

3 PCA提取主分量信息

主分量分析PCA(Principal Component Analysis)是一种用于探索高维数据结构的技术，主要思路是将n维数据投影到k(n>k)维空间超平面上，使各个样本点到超平面的投影距离最小且方差最大。它可以把可能具有相关性的高维变量合成线性无关的低维变量，新的低维数据集尽可能保留了原始数据的特征。具体步骤如下：

(a) 温度实测曲线

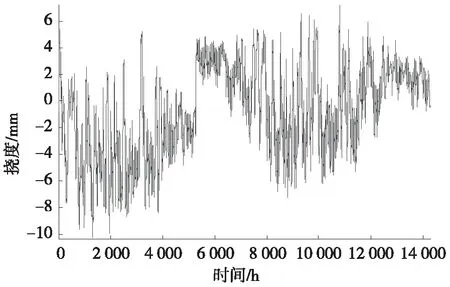
(a) 挠度实测曲线

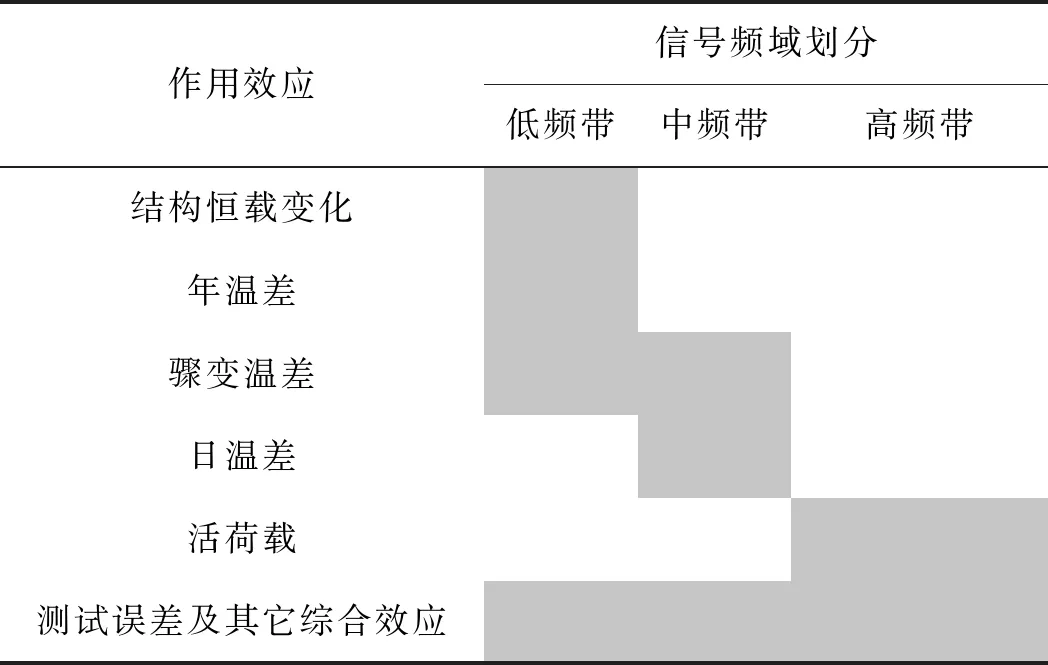
作用效应信号频域划分低频带中频带高频带结构恒载变化年温差骤变温差日温差活荷载测试误差及其它综合效应

1) 将原始数据中每个样本用一个向量表示，然后把所有样本组合起来构成一个矩阵X；

2) 计算该矩阵的协方差矩阵；

3) 求协方差矩阵的特征值和特征向量；

4) 将特征向量按特征值由大到小降序排列；

5) 计算贡献度，贡献度=前k个特征值之和/总特征值之和；

6) 取前k个特征向量组成矩阵P，通过计算XP得到重构(降维)后的数据Y。

通过前述方法去除或减小活荷载效应、短时温差(日温差及骤变温差)效应以及随机干扰误差的影响后，利用PCA对低频段信息进行降维，以保留90%原始信息的主分量作为最终评价指标。

4 工程应用

图3是自2015年11月4日至2017年2月26日国内某实桥应变测点S1-4的监测曲线。由图3可知，在2016年8月前应变值随温度变化而变化，其中最小值为88 με，最大值为404 με，均值为235 με，波动量为316 με，标准差为84 με，呈现出较为明显的正相关特性。但此后，尽管温度值不断减小，应变监测值也有减小趋势，但明显有异于历史监测规律，应变值始终处在一个高位水平(300 με)。

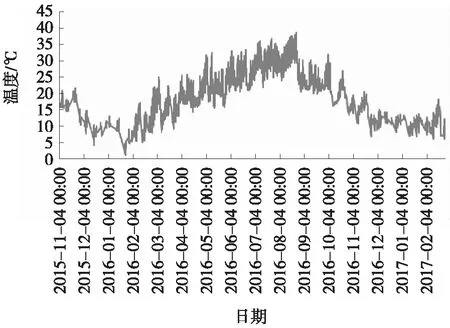
图3 S1-4实测曲线

图4是采用PCA频域分析方法考察测点S1-4在监测周期内主分量信息的变化情况，曲线反映的是恒载作用与长周期温度荷载作用下结构的综合响应。从图4可以看出，曲线呈现不断上升趋势，在2016年8月17日后始终处于一个较高水平，曲线变化规律与历史监测情况明显不同。出现这一现象的原因可能是该测点附近产生了微裂纹，使得应变监测值不再反映桥梁结构的真实响应。

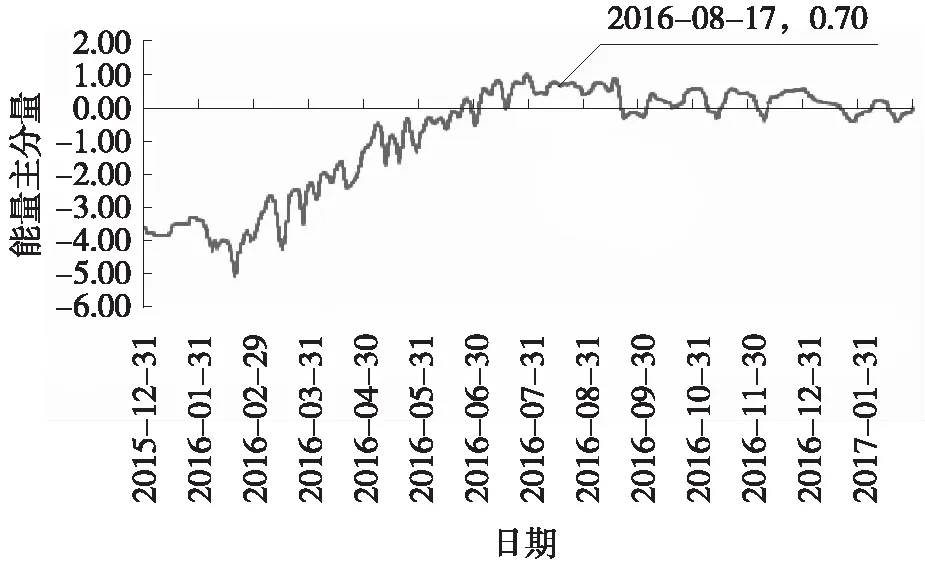
图4 S1-4主分量变化情况

图5是该测点温度与应变值在监测周期内互相关系数的变化情况(以5 000个采样点为一个数据段，依次递进进行互相关分析)。从图5可以看出，前期应变与温度具有强正相关特性(相关系数大于0.8)，但从2016年8月17日开始，相关系数不断减小(已低于0.8)，说明应变与温度逐渐偏离，应变受其他因素影响，已逐渐失去与温度的强相关特性。这一现象同样验证了前述PCA频域分析结论。

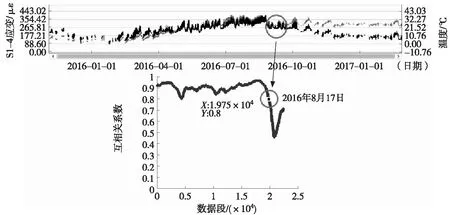
图5 S1-4应变与温度相关系数

5 结束语

为了从海量监测数据中找出直观评价桥梁结构运营实况的有效信息，基于PCA桥梁静态监测数据，通过理论推导提出了频域分析方法，经综合研究，对该法认识如下：

1) 频域分析方法能有效分离响应信号中的多种组成成分，在保留关键信息的同时能提高信噪比，凭此所构建的主分量评价指标能更加准确地表征桥梁运营状态。

2) 数值仿真计算也验证了该法对结构监测综合响应可在频域内完成多组分分离的情况，表明了该法的可行性。

3) 该法从原始监测综合响应中可去除短时温差效应、减小活荷载及随机干扰误差的影响，实桥应用案例验证了其有效性，为桥梁安全监测数据分析提供了一种新颖、有效的途径。