考虑风电场集群效应的高比例风电电力系统稳定性研究

池瑞枫，刘 莉，王 铎

（1.沈阳工程学院a.研究生部；b.学术委员会，辽宁沈阳 110136；2.国网辽宁省电力有限公司，辽宁沈阳 110006）

1 高比例风电电力系统稳定性分析原理

目前，适用于含有高比例风电电力系统暂态稳定性分析方法大致分为两种。一种是直接法中的暂态能量函数法，该方法是将系统构建成一个关于暂态能量的函数，并通过检查该函数的时变性来确定非线性系统的稳定性质。直接法是一种定性的方法，仅限于比较简单的数学模型，因此，在高比例风电电力系统中其分析结果尚不能令人满意。在高比例风电电力系统中风电不可控，风电系统中逆变器使得风机与系统解耦，这在高比例风电系统中就导致了系统的暂态稳定分析机理发生变化，吸引域无法确定，使得原本分析暂态稳定性的直接法不再适用于高比例风电电力系统。而第二种是时域分析方法，其基本思想是用数值积分方法求出描述受扰动微分方程的时间解，适用于各种不同详细程度的元件数学模型，可以通过选取不同精确的模型来满足不同的研究目的，分析结果准确、可靠。

高比例风电电力系统的暂态稳定分析常用微分-代数方程来进行求解，其中微分方程组用来描述系统动态特性，而隐式梯形法从计算速度、精度、数值稳定性、对刚性微分方程的适应性及计算的灵活性等方面考虑都较其他方法在高比例风电电力系统中有着更好的适应性。

隐式梯形法首先需要构建元件的一阶微分方程：

对于式（1），当tn初函数值xn已知时，可以按下式求出tn+1=tn+h处的函数值xn+1：

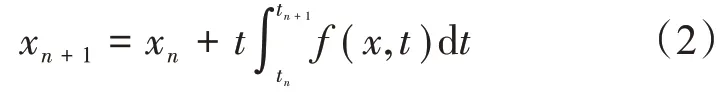
当步长h取值极小时，函数f(x,t)在tn～tn+1之间的曲线可以近似地用较短的直线来代替。因此，采用这种逐步逼近的方法，式（2）可改写为

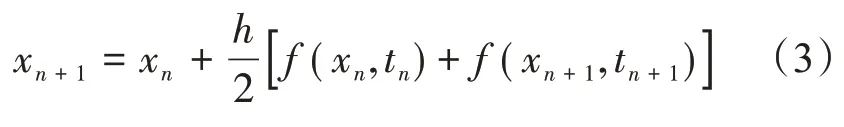
式（3）为隐式梯形法的差分方程，因为等式两边都存在xn+1，所以需要采用求解代数方程式的方法求解xn+1。

当初值t0、x0一定时，根据式（3）可以求得第一次迭代的方程：

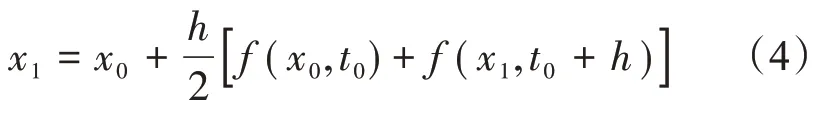
式（4）中只有x1未知，通过迭代可以解出x2，依次类推。

当用式（3）求解微分方程组时，整个计算工作变为求如下方程的联立解：

对此，非线性方程组的交替迭代求解步骤如下：

1）给定yt+Δt的初始估计值，应用式（5）得到xt+Δt的估计值，即求解方程=x(t)+

2 考虑集群效应的风电机组模型

2.1 考虑转动惯量的风机模型

因双馈风力发电机可实现有功、无功解耦控制，且照价维护成本较低，在未来很长一段时间内将会是风电机组的主要机型，因此本文所做研究皆以双馈风电机组为例。在高比例风电电力系统中，当发生故障而导致电压急剧降低时，风力发电机机组中的风轮机及转动轴的机械暂态特性与风力发电机的电磁暂态特性存在强相关性。但是，在暂态过程中，电磁暂态的持续时间要远远小于机械暂态的持续时间，而且风轮机及传动轴的转动惯量（即惯性时间常数）仅与其自身质量、机械转矩等自然物理特性有关，不会随着系统故障后发电机电磁转矩的变化而变化。因此，在系统中发生故障导致电压降落时，可以忽略电磁暂态对风电机组的影响。在分析对风电机组的影响时，可将机械转矩的变化看作类似阶跃响应的突变量：

式中，U=[Tm-Teo]T。

传动系统的初始状态为

阶跃输入下状态方程的通解为

由式（8）可知，风轮机转速、发电机转速、传动轴转矩可以分别表示为式（9）、式（10）、式（11）：

式中，Ht、Hg分别表示风轮机及齿轮箱低速侧（以下简称风轮机）、感应发电机及齿轮箱高速轴侧的惯性常数，同时Ht=Ht1+Ht2；ωt、ωg分别表示风轮机侧、发电机侧的角速度；Dt、Dg分别表示风轮机侧、发电机侧的阻尼系数；Dtg为传动轴的阻尼系数；Ktg为传动轴的刚性系数；Ttg为传动轴的扭矩；ω0为风力发电机组中传动轴的固有频率；τm为风力发电机组在受到扰动后的机械暂态过程的惯性时间常数。

通过式（9）和（11）可以看出在系统中发生电压降落时，风电机组的转动惯量具有如下特性：

1）传动轴的刚性系数和风轮机、发电机侧的惯性时间常数等自然属性决定了传动系统的固有频率。由于Ht＞＞Hg，固有频率近似为，从而可知随着传动轴刚性系数的增加、发电机侧的惯性时间常数的减小，传动轴的固有频率越大，发电机的转动惯量越小，受到扰动后的反应更为剧烈。

2）传动轴扭矩包含按ω0交变衰减分量和恒定的分量。由于Dtg很小，忽略Dtg和Hg，由式（11）可得：

由式（12）可见，无论传动系统是否处于稳定运行状态，传动轴扭矩最终接近电磁转矩。由于电压跌落时Ttg0＜Te，则由式（12）可知，在ω0t=π时，扭矩达到最大值，其最大值为

在电压跌落时，传动轴上存在很大的扭矩，因此在高比例风电电力系统中，如要对系统的稳定性进行分析，则风电机组的自身转动惯量不容忽视，否则会影响系统稳定性分析的准确性。转动惯量的体现可以更好地表现出风电场间在受到系统扰动影响后的不同的反映状态。

2.2 风电场集群效应原理及模型

在高比例风电电力系统中，风电装机容量占系统中总装机容量比例较大，此时如果忽略风电机场的集群效应（即在扰动后风电场间、风电场与系统间的互动），则对系统进行稳定性分析时，势必会对结果的准确性、可靠性产生影响。双馈风电机组的转子侧励磁电压来自电网，机组对机端电压的跌落非常敏感，当系统中发生大扰动而造成电压急剧跌落时，双馈风电机组的内部电气震荡会变得更加剧烈。在原有对高比例风电系统的仿真过程中，风电机组均被当作电源或负的负荷进行处理。本文考虑了电压保护控制策略，可以使风机响应系统发生大扰动后的暂态变化，以此来体现出风电场间的集群效应。

改进的发电机模型包括电压保护控制策略，如图1 所示。低压有功控制模拟实际系统的快速调节器及变流器锁相环控制功能，可以跟随系统故障后风电场并网点的电压变化，降低有功功率输出，减轻系统压力，增加无功出力，抬升风机出口电压，使得风机不至于发生解列情况，同时有功电流控制信号具有顶值限制和爬坡速度限制。在系统中发生故障导致风电场电压升高时，可以调整风机以减少无功电流，限制机端电压升高。电压保护曲线如图2所示。

图1 电压保护策略

图2 电压保护策略响应

考虑风电场集群效应后，使各风电场在系统中发生扰动时能体现不同的反映状态，而这种有功无功的快速变化对系统产生二次冲击，使系统的稳定性较未考虑集群效应时变得更加复杂，虽稳定性会变差，但更接近于真实情况。风电场响应集群效应流程如图3所示。

图3 风电场响应集群效应流程

3 仿真分析

通过CYME 电力系统仿真软件搭建辽西某市220 kV 仿真模型，其中220 kV 以下系统均等效为负荷进行处理，负荷模型采用40%恒阻抗、60%感应电机模型，发电厂调速机模型采用IEEE 模型，仿真如图4所示。

图4 220 kV实例仿真

故障设置为系统内L68 点发生三相短路，故障切除时间为0.12 s，将风机模型改变前、后的暂态稳定性情况进行比较。图5 为发生三相故障后风机出口母线电压的变化情况。

在电压恢复期间，不同风电场因受到扰动的程度不同，所导致电压抬升结果不同，距离故障点较近的风电场电压抬升较快，而较远的风电场受到扰动较小则变化相对较慢，并且在电压恢复到1.0 标幺值附近时，风电场无功减少，有功增加，导致电压会发生二次跌落现象，之后电压随着系统及风电场间共同调节作用逐渐趋于稳定。

图5 故障后风电场出口母线电压变化情况

表1 仿真对比分析

仿真对比分析情况如表1 所示，在考虑风电场集群效应和未考虑风电场集群效应情况下的频率、电压、功角的变化曲线如图6～图11所示。

图6 考虑风电场集群效应频率变化曲线

图7 未考虑风电场集群效应频率变化曲线

通过仿真对比分析表1及图6～图11可以看出，考虑风电场集群效应后，系统的稳定性较未考虑之前变得更加复杂和严重，未考虑集群效应之前，风电场仅仅被当作一个可变电源，无法参与到系统的稳定性调整中来，因此仿真分析出的结果过于片面。在低比例风电电力系统中也许对仿真结果影响不大，但在高比例风电电力中风电场间的特性会直接影响系统的稳定性，集群效应的体现使各风电场在分析中不再是独立的个体，而是成为影响系统稳定甚至参与系统稳定性调整的一部分。在稳定性分析中，考虑风电场集群效应后得到的结果更准确、可靠、更接近于真实值。

图8 考虑风电场集群效应电压变化曲线

图9 未考虑风电场集群效应电压变化曲线

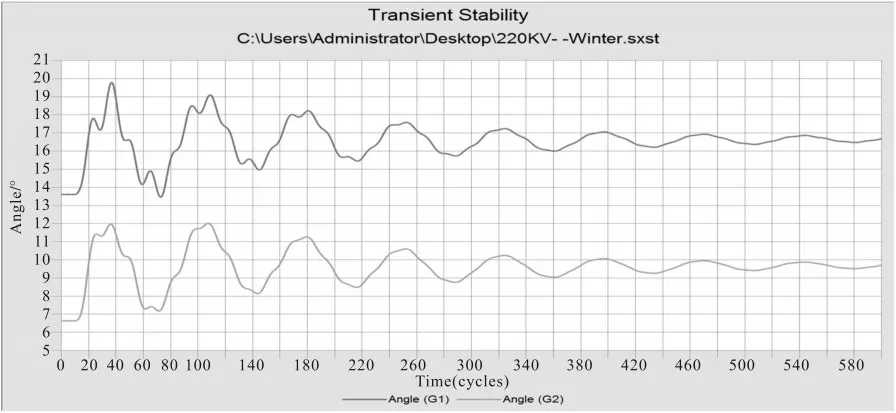
图10 考虑风电场集群效应功角变化曲线

图11 未考虑风电场集群效应功角变化曲线

4 结论

本文针对高比例风电电力系统在发生大扰动后风电场间集群效应无法体现的问题，在风电系统模型中考虑了电压保护策略，体现出各风电场在故障发生后功率变化的情况，解决了原有含风电电力系统在仿真中风电场间作为独立个体，不参与到系统稳定性影响中的缺点。通过220 kV 实例仿真验证，在考虑风电场集群效应后，系统的稳定性变差，与未考虑风电场集群效应时相比变得更加复杂。因为在系统发生扰动后，考虑集群效应时，风电场的有功无功出力受到电压保护策略的影响而发生变化，会对系统的稳定造成二次冲击，所得仿真结果更接近于实际情况。