面向安全威胁的铁路网络防御策略研究
朱广劼
(中国铁道科学研究院集团有限公司 电子计算技术研究所,北京 100081)
当前,铁路网络攻击行为在规模与攻击手段上不断升级,带来的安全威胁日益严峻。针对铁路网络规模庞大、结构复杂度高、安全要求高等特点,基于动态攻防博弈模型,初步探讨面向安全威胁的铁路网络防御策略。
1 网络安全策略研究现状
当前,关于网络安全的研究已经从传统的互联网安全延伸到特定的网络领域[1-3]。针对网络安全问题,学术界以及工业界从技术和实际应用的角度研究关键信息基础设施的特点,结合实际应用场景以及安全防护需求,给出工程上的安全防护方案或理论上的前期探索[4-8]。在网络安全威胁研究方面,有学者对网络攻击行为进行宏观建模并给出实际分析,通过建立宏观网络攻击模型,提出社交网络攻击的传播模型[9]。在网络安全态势感知方面,有学者根据恶意攻击下的网络设备受到的影响,提出态势感知策略,利用KDD Cup99进行数据仿真,给出网络安全感知效果。在电力系统领域,有研究人员在分析其信息物理系统模型的基础上,对网络攻击建模,研究系统的脆弱性[3]。还有研究人员对拒绝服务攻击下信息物理系统的脆弱环节进行预测与研判[10-11]。在风电系统领域,有研究人员针对系统网络安全的控制与趋势预测,利用攻击树的概念,分析系统中受到的安全威胁,研究攻击防御对策,对攻击树叶子节点进行量化分析,给出安全威胁因素的入侵路径[12]。
2 铁路网络系统复杂性特点与安全要求
作为我国关键行业之一,铁路在完成货物运输、旅客服务等任务过程中,铁路网络系统发挥着关键作用,铁路安全生产对网络性能和安全均有较高要求。目前,铁路在国内重点地区实现完全可达,要求铁路网络系统实现全面覆盖,铁路网络所承载的应用种类多、数量大。由于各类应用的业务需求差别较大,导致铁路网络规模大、结构复杂,如执行运输、列车调度等任务的应用要求闭合网络结构,而旅客服务应用则要求接口开放、多终端接入。
3 面向铁路网络的层次动态攻防博弈模型
3.1 层次攻防博弈模型简介
在解决复杂问题建模以及计算方面,复杂系统理论以及动态规划模型给出一种可行的解决策略。随着防护策略的可用性不断增强以及博弈论的研究深入,有研究提出多层规划模型[13]。
对于一个层次决策模型,根据其决策层的功能以及决策流程,表达式如下所示:
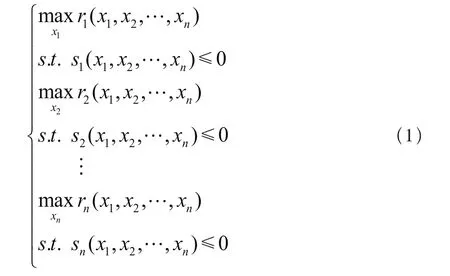
其中,xi(i=1,2,…,n)是每一层的决策变量,ri(x1,x2,…,xn)(i=1,2,…,n)表示第i层的决策函数;si(x1,x2,…,xn)(i=1,2,…,n)表示第i层决策函数需要满足的约束条件。
由式(1)定义的层次决策模式采用从上至下的分层决策方式:(1)由在满足第1层约束条件的前提下确定决策变量值x1;(2)由第2决策层即确定该层的决策变量值x2;(3)在此基础上,依次由下一层分别确定各自的决策变量,最终完成本轮攻防博弈模型中的决策变量值求解。一轮决策过程完成后,根据实际决策效果,从上至下由上层根据下层的决策效果反馈进行相应的决策值调节,通过多次循环执行,使得整个系统达到最优化状态。
3.2 面向铁路网络的层次动态攻防博弈模型
根据层次攻防博弈模型的构建思想,可按功能层次将面向铁路网络的动态攻防博弈模型的构建划分为网络防御与资源控制、攻击方案以及攻击造成的损失3个步骤:(1)在构建攻防博弈模型时,首先进行防御方案制定和防御资源分配,且需要考虑当前网络实际情况,如防御资源限制等因素;(2)当攻击者获得防御策略部署及防御资源分配后,制定相应的攻击效果最大化方案;(3)在攻击者发起攻击的基础上,针对攻击者的策略以及防御策略和资源分配,采取相应的措施来降低最终损失。
在防御策略部署及资源分配中,可考虑网络防御者综合已有的防御资源和可以执行的防御策略,以区域分布或地理位置分布的方式将防御资源部署在相应的运行系统中。在防御策略上,通过决策者调用防御资源,可以在网络系统局部遭到攻击后实现快速资源调动和支援响应。在防御策略部署和资源分配中,要在有限资源和防御策略的限制下最大程度保障网络的运行。
非法用户针对网络防御策略制定攻击方案,根据已有的防御资源和掌握的信息,尽可能最大化自身的攻击效果。
在网络遭到攻击后,根据攻击的形式及可能造成的后果来降低损失。在生成该层策略时,若通过优化已有的防御资源配置等方案仍然不能满足网络正常运行的要求时,应及时采取应急措施。在该层模型中,需要研究已有的资源分配和攻击方案,通过合理的措施使攻击造成的影响最小。
显然,枝节的改革无补于大局。诚如有学者肯定其良好的愿望和一定的实际成效后指出:“它的改良主义的政治出发点、依赖地方政府和国内外社会力量资助的经费来源,及其所推行地区和所取得实际成效的局限性,相对于当时半殖民地半封建社会的国情背景和普遍贫穷的广大农村,显然不能成为乡村建设派所期望的解决近代中国农村问题的有效途径,更不能成为解决近代中国问题的根本之路。”[34]
4 铁路网络3层攻防博弈模型及其求解方法
4.1 铁路网络3层动态攻防博弈模型的构建
铁路网络3层动态攻防博弈建模涉及防御方案制定以及防御资源分配、攻击者实施攻击和降低攻击所造成的损失3个环节。
防御方案制定和防御资源分配:假设铁路网络内的攻击目标有ND个,对于铁路网络内第i个攻击目标,令Imin表示降低该目标被攻击概率所需要的最小资源分配,Im表示该目标的实际资源分配,Pm(Im)表示该目标遭到攻击的概率,则可以得:

其中,αm=-ln(qm0)/Imin。
根据实际防御中的防御资源调控,设防御资源的最大值为Itotal,防御资源分配需满足以下约束条件:

针对具体防御方案,其遭到网络攻击后所造成的综合损失定义为:

其中,PC,i表示第i个终端节点遭到攻击后造成的损失。
该层的目标函数为:

其中,PC为该防御方案下,攻击者在成功攻击且防御者采取措施后造成的损失。
攻击者选择攻击效果最大化的方案,而防御者则在遭到攻击后采取最优化的措施来减少攻击造成的损失。根据当前非法入侵者的实际情况,假设非法攻击者已经掌握防御层的防御策略和防御资源分配,该层的目标函数可以表示为:

攻击者采用非法入侵的方式,在一定程度上会引起网络流量的变化,其约束条件表示为:

其中,μ是调节因子,可以根据已有的情况来设定,Qi表示第i个终端节点正常运行时的流量。
该层模型在研究防御策略以及攻击者攻击方式的基础上,最大程度地降低攻击所造成的损失,其目标函数为:

其中,PC,i表示第i个终端节点受到攻击后造成的损失。非法入侵最直接的影响是引起网络流量的变化,对流量进行约束可从源头上实现对攻击的识别,以及对现有资源误差的建模,其约束条件可以表示为:

其中,PS,i表示入侵后的网络流量,PD,i表示网络正常运行时的流量,Qmax表示当前节点能够容纳的最大流量,λ是调节因子,表示由非法入侵者造成的流量与其造成的损失之间的关系,且λ∈R。
4.2 铁路网络3层动态攻防博弈模型求解方法
非线性多层模型的直接求解方式效率较低,且求解过程中收敛性较差。对于铁路网络,由于网络节点有限,且防御资源与防御决策、攻击方案等均有限,在攻击方和防御方都采用对自身最优化的方式时,通过计算攻击造成的损失并采取相应的防护措施,可达到两者的平衡,即可求得相应的均衡解;求解流程见图1所示。
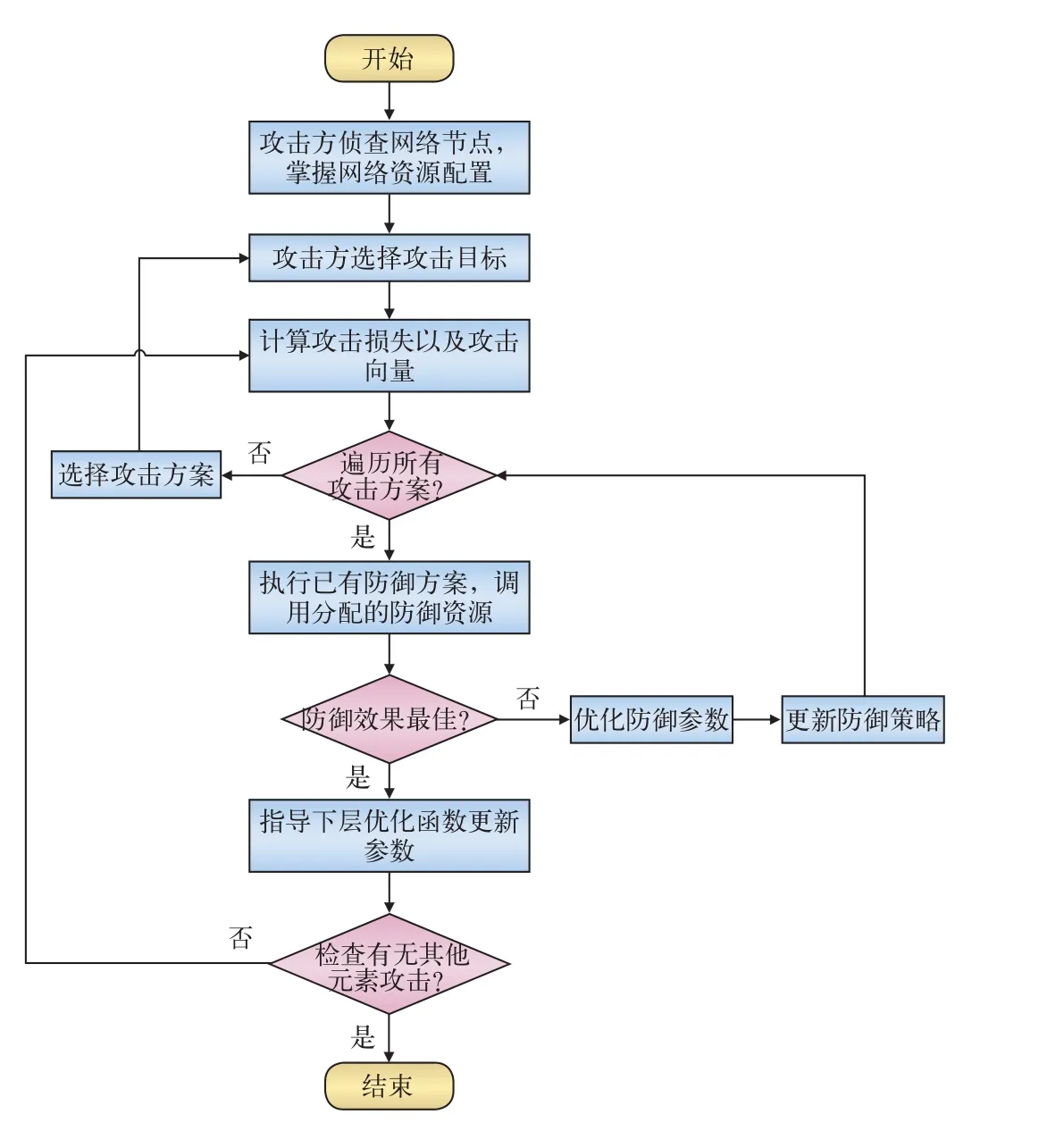
图1 铁路网络3层动态攻防博弈模型的求解流程
5 结束语
研究面向安全威胁的铁路网络防御策略,基于层次攻防博弈模型,提出铁路网络3层动态攻防博弈模型的构建方法,给出各层优化函数与求解流程。
今后需要结合铁路网络不同层次的具体防御资源配置与安全要求,研究制定具有针对性的可行求解策略。

