路堤荷载下短混凝土芯碎石桩复合地基的固结特性

翁嘉蔚, 杨 涛

(上海理工大学 土木工程系， 上海 200093)

混凝土芯砂石桩是在砂桩或碎石桩的中心插入预制混凝土桩形成的复合材料桩，它作为不排水的刚性桩与排水的散体材料桩相结合的产物与桩间土一起形成复合地基。由于混凝土芯砂石桩复合地基具备刚性桩复合地基承载力高和散体材料桩复合地基固结快的双重优点，在国内外开始得到应用[1-2]。

许多学者对混凝土芯砂石桩复合地基的承载特性展开了研究。陈俊生等[3]、唐彤芝等[4-5]和程万钊等[6]进行了路(坝)堤荷载下悬浮混凝土芯砂桩复合地基的现场试验，通过实测芯桩、砂桩壳和桩间土的荷载分担、桩间土表面沉降和分层沉降、桩-土差异沉降、桩间土孔压和坡脚处地基土的水平位移发现：刚性芯桩承担了大部分路堤荷载，砂桩桩壳的存在使复合地基的固结远快于刚性桩复合地基，芯桩上部出现负摩阻力。鲁绪文等[7]、唐彤芝等[8]和叶观宝等[9]分别利用圆孔扩张理论、现场试验和有限元法研究了振动沉管法施工的混凝土芯砂石桩的挤土效应，研究发现：混凝土芯砂石桩的挤土效应远小于刚性桩，砂石桩壳对沉桩引起的超静孔压和深层水平位移累积有明显的消散作用。叶观宝等[9]还研究了刚性基础下混凝土芯砂石桩复合地基的荷载传递特性，发现芯桩为摩擦桩，它承担了大部分荷载并通过桩侧摩阻力传递给地基土。近些年来，混凝土芯砂石桩复合地基的固结特性和固结计算方法受到学者们的高度关注。Zheng等[10]和Jiang等[11]采用三维有限元方法研究了刚性基础下端承水泥土芯砂桩复合地基的固结特性，计算发现：同等条件下水泥土芯砂桩复合地基的固结速率与砂桩复合地基较为接近，显著快于水泥土桩复合地基，它随芯桩刚度的增加而增大。此外，Jiang等[11]还获得了荷载在桩间土-芯桩-砂桩壳间的传递规律。一些学者在等应变假设下建立了混凝土芯砂石桩复合地基的固结解析解[12-17]，可以考虑涂抹效应、砂石桩壳的径向渗流、地基土中附加应力不均布和非线性、荷载随时间变化、复合地基顶面和底面部分排水等因素的影响。杨燕伟[18]建立的固结解答可以考虑芯桩与砂石桩壳和桩间土间有不同的沉降。叶观宝等[19]基于等应变假设，提出了真空联合堆载作用下混凝土芯砂石桩复合地基固结解析解。张绍勇等[20]、冯艳辉等[21]和袁展强等[22]推导单一材料桩的固结解答，学者们利用这些固结解析解分析了一些主要因素对复合地基固结速率的影响。

虽然混凝土芯砂石桩复合地基固结问题的研究已取得了相当进展，但数值分析成果和固结解析解大都是针对刚性基础下的端承等芯混凝土芯砂石桩(芯桩与砂石桩壳长度相等)复合地基取得的。目前，路堤下的软基常采用悬浮混凝土芯砂石桩复合地基加固，工程设计中芯桩长度需要结合工程地质条件等多因素确定，芯桩不一定穿透砂石桩壳。为了深化混凝土芯砂石桩复合地基固结特性的认知，很有必要深入研究柔性基础(路堤)下短混凝土芯碎石桩(芯桩长度小于碎石桩壳，本文简称“SCCS桩”)复合地基的固结特性。鉴于此，本文采用有限元法数值模拟方法，研究路堤荷载下悬浮和端承短混凝土芯碎石桩复合地基的固结特性，成果可为今后短混凝土芯砂石桩复合地基固结计算模型的建立奠定基础，为类似工程设计提供参考。

1 有限元模型的建立

(1) 几何模型与荷载施加。大面积路堤荷载下的软土地基采用短混凝土芯碎石桩(SCCS桩)加固。利用对称性，基于Unit Cell概念，选取轴对称复合地基有限元固结分析模型如图1所示。复合地基总厚度H=20 m，路堤高度h=4 m，120 d完成填筑。短混凝土芯碎石桩复合地基几何基准参数如下：单个SCCS桩影响区半径re=1 m，碎石桩壳半径rp=0.25 m，SCCS桩的置换率m=(rp/re)2=0.0625。混凝土芯桩半径rc=0.115 m，芯桩截面含芯率ρ=(rc/rp)2=21.16%。涂抹区半径rs=1.5rp=0.375 m。考虑SCCS桩悬浮和打穿软土地基二种情况：① SCCS桩悬浮，长度H2=17 m，其贯入比α=H2/H=0.85。芯桩长度H1=12 m，芯长比β=H1/H2=0.71；② SCCS桩打穿软土，H2=H=20 m， SCCS桩的贯入比α=1.0，芯长比β=0.71。

图1 有限元模型

(2) 边界条件。利用对称性，取图1几何区域二分之一计算。模型左侧边界为对称轴，右侧边界为模型外边界，这两个边界上的径向位移约束，不排水；模型底边界径向和竖向均约束，不排水；复合地基顶面为自由边界，排水。

(3) 材料本构模型及参数。混凝土芯桩采用线弹性模型，碎石桩、地基土和路堤土采用摩尔-库仑模型。各材料模型参数和渗透系数见表1，表中kph和kpv分别为碎石桩壳的径向和竖向渗透系数，kh1和kv1分别为未扰动桩间土的径向和竖向渗透系数。桩间扰动区土的径向渗透系数为ks=5×10-9m/s，其竖向渗透系数和其他力学参数与未扰动区桩间土相同。表中括号中的数据为材料的压缩模量。各材料弹性模量E可由其压缩模量Es和泊松比μ按式E=(1+μ)(1-2μ)Es/(1-μ)近似换算。

表1 材料模型参数

碎石桩壳-芯桩之间和碎石桩壳-土交界处设置摩擦接触对，参照文献[9]，芯桩与碎石间摩擦系数为0.4，碎石桩壳与地基土间的摩擦系数为0.3。

(4) 网格划分。采用大型有限元软件ABAQUS进行数值计算。混凝土芯桩和路堤土采用4结点四边形单元CAX4划分，碎石桩和地基土采用应力-孔压耦合4结点四边形单元CAX4P划分。图2给出悬浮SCCS桩复合地基有限元网格，结点总数为2 892个，单元总数为2 640个。

图2 有限元网格图

2 有限元模型验证

为评价所建SCCS桩复合地基固结分析有限元模型的合理性，采用上述建模方法建立轴对称有限元模型分析文献[11]中刚性基础下端承水泥土芯砂桩复合地基固结特性。水泥土芯砂桩复合地基厚度10 m，单桩影响半径为1.25 m。砂桩壳长10 m，半径为0.425 m。水泥土芯桩与桩壳长度相等，半径为0.25 m。复合地基表面设置厚度0.5 m的刚性板，板上均布荷载100 kPa瞬时施加。模型底边界各方向全约束，不排水，左、右两个侧面法向位移约束，不排水。复合地基顶面为自由边界，排水。水泥土芯桩-砂桩壳之间和砂石桩壳-地基土之间为完全接触。水泥土桩和砂桩壳采用摩尔-库仑模型，地基土采用线弹性模型。桩和地基土的本构模型、模型参数和渗透系数均与文献[11]相同。考虑水泥土桩渗透性，水泥土芯桩和砂桩壳采用应力-孔压耦合4结点四边形单元CAX4P划分，地基土采用4结点四边形单元CAX4划分。图3给出本文有限元和文献[11] 3D有限元计算的按沉降定义的复合地基固结度Us随无量纲时间Tv=cv1t/H2变化曲线，cv为地基土的固结系数。由图3可知，本文有限元计算获得的复合地基固结度曲线与文献[11]计算结果较为一致，二者最大差值约为4%。算例表明本文有限元模型具有较高的计算精度，可用于短混凝土芯碎石桩复合地基固结特性的数值分析。

图3 不同有限元法固结度曲线的比较

3 复合地基固结特性

下面从两方面研究端承和悬浮SCCS桩复合地基的固结特性:首先对比混凝土桩复合地基、碎石桩复合地基和SCCS桩复合地基的固结速率，然后对SCCS桩复合地基进行参数分析，研究几何和力学参数的变化对其固结速率的影响，基准的几何和力学参数见前述有限元模型。

3.1 不同复合地基固结速率的比较

图4给出有限元计算获得的悬浮与端承SCCS桩复合地基固结速率与相同长度和直径的混凝土桩复合地基和碎石桩复合地基计算结果的比较，横坐标采用无量纲时间因数Th=ch1t/de2，ch1=kh1Es1/γw。图4表明，无论桩体是否打穿软土，混凝土桩复合地基固结最慢，SCCS桩复合地基的固结速率次之，碎石桩复合地基固结最快，但SCCS桩的固结速率与碎石桩复合地基非常接近。可见，在碎石桩中插入刚性芯桩，不仅大幅提高了复合地基承载力，也几乎没有降低原来碎石桩复合地基的固结速率。

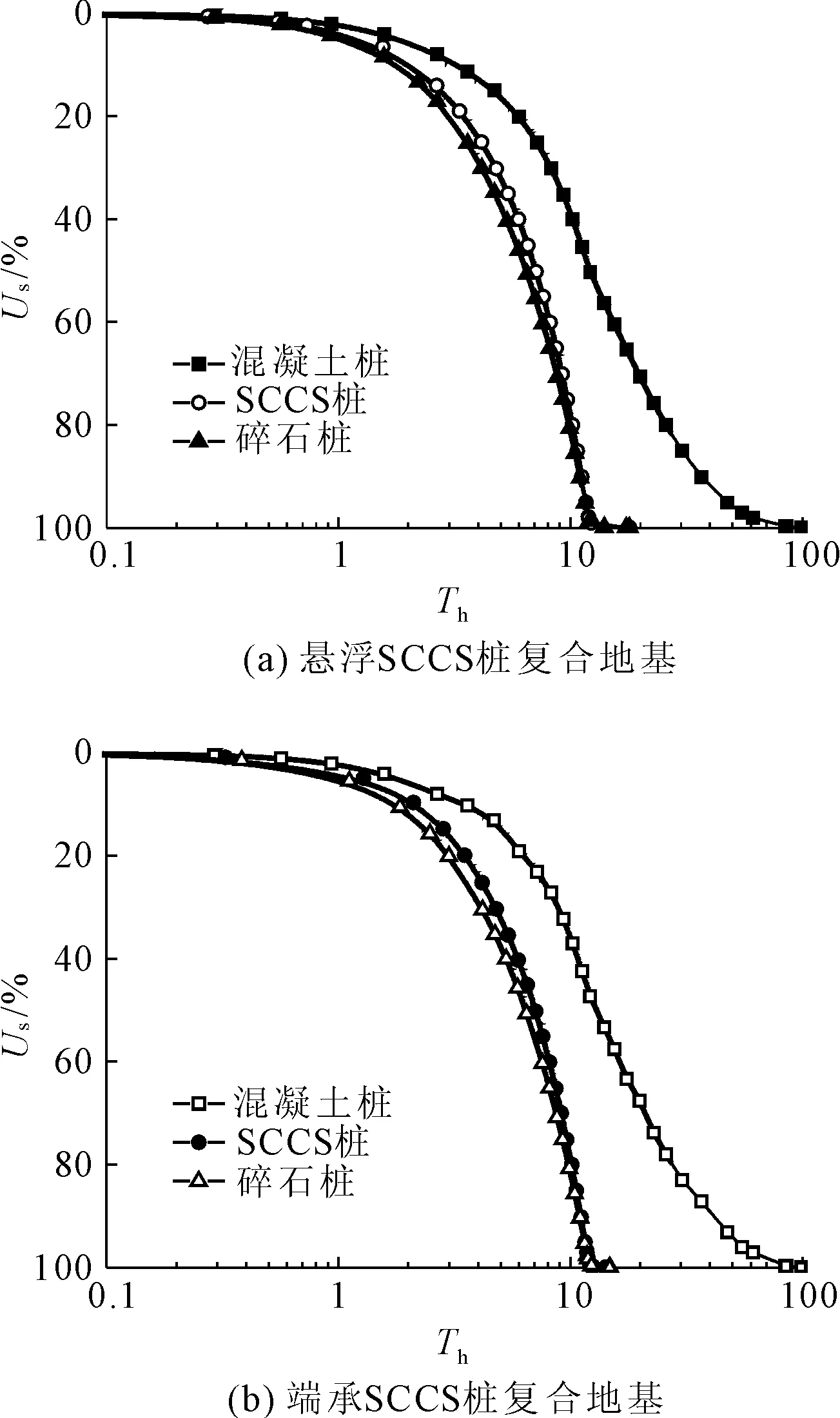
图4 不同竖向增强体复合地基固结速率的比较

3.2 固结速率影响因素分析

(1) 混凝土芯碎石桩贯入比。图5给出不同SCCS桩贯入比下悬浮SCCS桩复合地基的固结度曲线，计算时地基土均质，压缩模量为3 MPa，芯桩长度H1=9 m保持不变。从图5可见，悬浮SCCS桩复合地基的固结速率随其贯入比的增加而增大。这是由于随着碎石桩壳长度的不断增加，越来越多的桩间土和下卧层土的排水距离逐渐缩短从而加快桩间土固结。这说明，端承SCCS桩复合地基的固结要快于悬浮SCCS桩复合地基。

图5 SCCS桩贯入比α对固结速率的影响

(2) 芯长比。图6给出不同芯长比β下端承和悬浮SCCS桩复合地基的固结度曲线。图6(a)是悬浮SCCS桩复合地基的计算结果，计算中SCCS桩贯入比α=0.85保持不变。β=0代表碎石桩复合地基，β=1时芯桩与碎石桩壳长度相等，为悬浮等混凝土芯碎石桩复合地基。

图6 芯长比β对固结速率的影响

从图6(a)中可以看出，随着芯长比的增加，悬浮SCCS桩复合地基的固结速率逐渐变小。原因在于芯长比增加，不排水芯桩的长度增大。由于芯桩是悬浮桩，悬浮芯桩长度的增加只能使SCCS桩复合桩地基的固结速率小幅增大。然而，其下碎石桩壳长度的缩短会使SCCS 桩复合地基的固结速率减小，其减小幅度超过了前者增加的幅度。总的来看，混凝土芯桩长度的变化对悬浮SCCS桩复合地基的固结速率影响较小。图6(b) 给出端承SCCS桩复合地基的计算结果。由图6(b)可见，对于端承SCCS桩复合地基，其固结速率随芯长比的增加先减小后增大。β=0时为碎石桩，此时复合地基固结速率最大，β>0时桩由碎石桩变为SCCS桩，复合地基的固结速率开始变小。芯长比β>0.5以后，悬浮不排水芯桩长度的增加加快了复合地基的固结，故桩端承SCCS桩复合地基固结速率又开始增大。总的来看，芯长比对端承SCCS桩复合地基固结速率的影响很小。综合图6(a)和图6(b)可知，无论是SCCS桩是否打穿软土，芯长比的变化对复合地基的固结速率的影响很小。

(3) 芯桩截面含芯率。为研究芯桩截面含芯率ρ的变化对SCCS桩复合地基固结速率的影响，图7给出不同芯桩截面含芯率下端承和悬浮SCCS桩复合地基的固结度曲线，计算中芯长比保持β=0.71不变。由图7(a)可知，悬浮SCCS桩复合地基的固结速率随芯桩截面含芯率的增加而略微变小。图7(b)表明，ρ从0.04增加到0.64时由于端承芯桩刚度的增加使复合地基的固结速率增大，但ρ>0.64以后复合地基固结速率反而减小，这是由于碎石桩体积减小引起复合地基固结速率减小的幅度超过了端承芯桩刚度增加引起复合地基固结速率增加的幅度。端承SCCS桩复合地基固结度曲线彼此靠的很近，说明端承SCCS桩复合地基固结速率受芯桩截面含芯率的影响较小。综合图7(a)和图7(b)可知，芯桩截面含芯率的变化对端承和悬浮SCCS桩复合地基固结速率的影响都很小。

(4) 芯桩刚度。图8给出芯桩-桩间土模量比Esp/Es1的变化对悬浮和端承SCCS桩复合地基固结速率的影响，Es1=3 MPa。考虑芯桩材料从水泥土变化到混凝土，Esp/Es1的变化范围取50～9 000。端承SCCS桩复合地基固结计算中考虑SCCS桩贯入比β取0.30和0.71二种情况。图 8(a)表明，由于芯桩和SCCS桩都是悬浮桩，随着Esp/Es1的增加，悬浮SCCS桩复合地基固结速率仅略微增大，芯桩刚度的变化对悬浮SCCS桩复合地基的固结速率影响较小。从图8(b)和图8(c)可见，与悬浮SCCS桩复合地基不同，芯桩刚度的影响与其长度有关：当芯长比较小(β=0.30)即芯桩较短时，随着芯桩刚度的增加，端承SCCS桩复合地基的固结速率仅略微增大此时芯桩刚度的影响较小；当芯长比较大(β=0.71)也就是芯桩长度较长时，端承SCCS桩复合地基的固结速率随Esp/Es1的增加显著增大。

图8 Esp/Es1对固结速率的影响

(5) 碎石桩壳刚度。为分析碎石桩壳刚度的变化对SCCS桩复合地基固结速率的影响，图9给出不同碎石桩壳-桩间土模量比Ep/Es1下悬浮和端承SCCS桩复合地基固结度曲线，Es1=3 MPa保持不变。由于实际工程中碎石桩压缩模量的变化幅度不大，计算中Ep/Es1变化范围取10～30。总的来看，碎石桩壳模量的变化对悬浮和端承SCCS桩复合地基固结速率影响很小。

4 结 论

(1) 无论SCCS桩是否打穿软土，SCCS桩复合地基的固结速率与相同尺寸的碎石桩复合地基非常接近，远大于同尺寸的混凝土桩复合地基。

(2) 悬浮SCCS桩复合地基的固结特性的固结速率主要取决于SCCS桩贯入比，贯入比越大，复合地基的固结就越快。芯长比、芯桩截面含芯率、芯桩刚度的变化影响很小。

(3) 端承SCCS桩复合地基的固结速率主要与芯桩的刚度有关。当芯长比较大时，芯桩刚度越大，复合地基固结速率的增加越显著。芯长比、芯桩截面含芯率的变化对端承SCCS桩复合地基的固结速率几乎没有影响。芯长比较小时，芯桩刚度的变化也不会影响复合地基的固结速率。