一题多空型数学填空题命制摭谈

余建国

填空题被称为数学高考命题的“试验田”，其命题形式、内容等方面都处在不断变革和完善之中，一题多空是命题技术创新的形式之一。［1］2004 年北京市数学高考试卷中开始出现一题两空，此后无论是分省命题，还是相对统一的三份全国卷都或多或少出现一题两空型填空题。本文在分析2019 年高考数学填空题的基础上，结合笔者的命题实践，［2］探讨一题多空型填空题的命制方法。

一、2019 年高考数学填空题“一题多空”分析

2019年高考数学试卷全国共计13 份：北京卷（文、理），天津卷（文、理），全国卷Ⅰ（文、理），全国卷Ⅱ（文、理），全国卷Ⅲ（文、理），以及文理合卷的上海、江苏和浙江。填空题均为“一空型”的有全国卷Ⅰ（文、理）、全国卷Ⅲ（文、理）、天津卷（文、理）以及文理合卷的上海卷和江苏卷，其余5 份试卷中都存在多空型的填空题，且均为一题两空。表1统计了5份含一题多空试题的填空题。

从表1 可以看出，一题多空型填空题都是一题两空，但试题的数量不一样，其中北京文、理卷中试题数量也有区别；从试题位置来看，命题人一般根据素材的类型和难度预估，按照难度次序从易到难排列，几乎都与一题一空混合排列，没有固定次序；考查的知识点或方法都是高中数学中的基础知识和基本方法，属于“双基”范畴。

试卷名称北京卷（文）北京卷（理）全国卷Ⅱ（文、理）浙江卷填空题个数多空题考查内容6 6 4 7多空题个数2（第14题文理同题）3（第14题文理同题）1（文理同题）4线性规划；二元一次不等式应用题等差数列的通项与求和公式应用；函数的奇偶性与单调性；二元一次不等式应用题有文化背景的立体几何计算题直线与圆的位置关系；二项式定理应用；解三角形；平面向量模的最值

选择题和大多数填空题属于“客观题”，这种题型在考查双基方面具有优势。而相对于解答题，由于没有过程分，填空题不能区别“一笔失误”与“根本不会”，因此区分度受到一定影响。为了保证信度，提升区分度，一题多空型试题在发挥一题一空题型优势的同时，设立了“中间站”，或体现局部结果，或作难度递进，既可以增加考查内容，扩大知识覆盖面，又可以将难度较大的问题让学生“分步得分”，如全国Ⅱ卷（文、理）第16 题，在卷面上明确了“本题第一空2分，第二空3分”。

二、一题多空型填空题的结构与命制

填空题通过提供一个不完整的叙述，让考生根据要求填写空缺的部分（定量或者定性），形成一个正确的命题，填写内容可以是条件，也可以是结论。在一空型填空题的基础上，一题多空试题设计形式更加多样化，结构上更加丰富多彩。

1.知识点并列式。

在一个主干知识下考查几个相关的知识点，使主干知识的考查更加突出，这在计算型填空题中比较普遍，如在等差数列中，先计算通项公式或特定项，再计算前n项和或计算前n项和的最值，难度上略有递进。并列式的多空问题之间知识内容、思维层次前后关系不紧密，各自独立求解，只是增加考查知识的覆盖面。

例1 设等差数列{an}的前n项和为Sn，若a2＝-3，S5＝-10，则a5＝____，Sn的 最 小 值 为____。（2019年北京卷理科第10题）

例2 在△ABC中，∠ABC＝90°，AB＝4，BC＝3，点D在线段AC上，若∠BDC＝45°，则BD＝____，cos∠ABD＝________。（2019 年浙江卷第14题）

从这两个例题可以看出，两空共享基本量的计算结果，但又各自独立求解，增加了考生得分的机会，同时使主干知识的考查更加全面。研究历年高考试题可以发现，这样的多空型填空题最多。

与此类似的试题还有2019 年北京卷理科第13题，2019年浙江卷第12、13题。

2.问题并列式。

这种并列式多空题，所考查的两个或多个问题往往是有关联的，它们是同一数学模型的多方面结果呈现。所以，在解题时数学模型的建立或解题方法的选择必须是正确的，在此基础上各个击破，先易后难。

与此类似的试题还有2018 年北京卷理科第14题，2018年浙江卷第12、13题。

3.阅读理解式。

这类问题往往给出较多的背景，尤以实际背景为多，题干较长，文字叙述较多，背景中蕴含某个数学问题（模型），考生通过阅读、理解、抽象及建模，才能得到通常意义上的数学习题。通过一题多空设问，考查学生对问题理解和解决的层次深浅，可以更真实地反映考生的阅读理解以及进一步学习的潜能。

例5 李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃。价格依次为60 元/盒、65 元/盒、80 元/盒、90 元/盒，为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120 元，顾客就少付x元，每笔订单顾客网上支付成功后，李明会得到支付款的80%。

①当x＝10 时，顾客一次购买草莓和西瓜各1盒，需要支付________元；

②在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为______。（2019 年北京卷理科及文科第14题）

除了与实际问题紧密相关的应用题，“新定义”题也能考查学生的阅读、理解和解决问题的能力，这类问题在填空题中，为了最大限度地发挥其甄别学生学习能力的作用，往往也设置成一题多空型。

类似的试题还有2019 年全国卷Ⅱ理科及文科第16题、2014年湖北卷理科第14题。

三、命制一题多空型填空题的新探索

纵观从2004 年开始出现的历年一题多空型填空题，除了上面粗浅的分类外，显然还有其他的命题技术。下面结合笔者的命题实践，从多空的结构角度例说若干命制方法。

1.从特殊到一般。

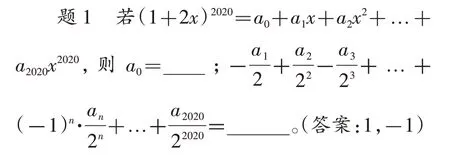
2.从静止到运动。

题3 斜率为k的直线l经过抛物线y2＝4x的焦点F，且与抛物线相交于A，B两点，①当k＝1 时，AB＝________；②点B关于x轴的对称点为B′，直线AB′过定点________。（答案：8，（1，0））

静止是运动的定格，运动是静止的连续。在函数、解析几何中，运动变化是永恒的主题，第1空设计为某特定的变量（位置）的问题，第2空研究变量（位置）任意取值（运动）时的问题，这类问题的结论往往与定量或定性有关。与此类似的还有——

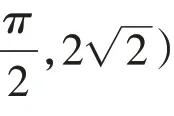
3.从确定到最值。

第1空需要解可行域的交点，并确定可行域的形状，为第2空数形结合奠定基础。两空由浅入深，由易到难，内在逻辑相连。在求最值类问题中，可设置前置问题，意在引导考生共享运算结果，防止重复计算。与此类似的还有——

题6 已知抛物线y2＝4x，过点P（4，0）的直线与抛物线相交于A（x1，y1），B（x2，y2）两点，则y1y2＝______，y12＋y22的最小值是______。（答案：16，32）

4.从正向到逆向。

一个命题的题设和结论都可能包含若干要素，只要部分或整体地交换这些要素，就可以构造原来命题的一个“逆向”命题，将难度小的放第1 空，难度大的放第2 空。这种逆向构造，既可检测学生对原有概念或命题的理解，又能促使他们发现一些有意义的新命题。事实上，本题中离心率、斜率与向量关系“3 倍”三者有着内在的联系，这种关系可以拓展到双曲线和抛物线，是解析几何久考不竭的“金矿”。与此类似的还有——

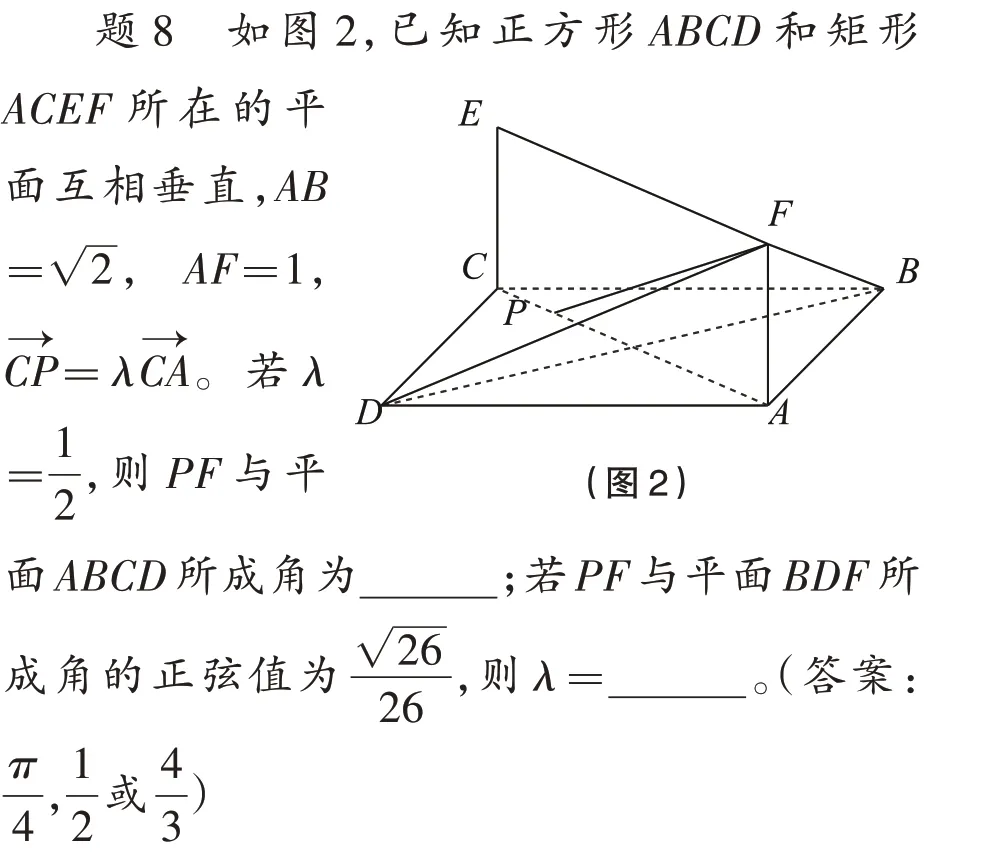
另外，开放性问题和探究性问题也已逐步进入数学试题，如前几年比较多见的类比和归纳，考查学生的归纳、类比、猜想、顿悟等非逻辑的推理能力，其特点正好适用于不需表达过程的填空题，但如何借助一题多空优势呈现，仍需命题者潜心研究。

题型是题目的呈现方式，是实现考查目的的重要手段。高考的考查目标和考查重点进行改革以后，需要新的题型呈现考查要求，实现考查目的。［3］笔者认为，命题技术能体现教师把握数学本质规律的能力，研究命题能够促进教师教学方式的变革。一题多空型填空题会因更多教师的参与研究而变得更加精彩。