高效安全的可审计盲混币服务方案

乔康，汤红波，游伟，李海涛

高效安全的可审计盲混币服务方案

乔康，汤红波，游伟，李海涛

（信息工程大学，河南 郑州 450001）

混币服务能够为区块链隐私泄露问题提供解决方案，但仍然面临效率瓶颈和安全风险，为进一步提升混币服务的效率和安全防护能力，提出一种高效安全的可审计盲混币服务方案。该方案首先增加了审计措施，在传统的混币模型基础上，增加审计区块链，以记录用户和混币器行为，实现可追溯和可问责；然后利用椭圆曲线算法构造盲签名，替代现有研究中基于双线性对或RSA的盲签名算法；最后基于可审计的混币模型和新构造的盲签名算法，提出可审计的盲混币服务协议。仿真分析表明，所提方案在提供隐私保护的同时，具有可审计性、抗盗窃攻击等6种安全特性；在同等安全强度下，较对比方案，所提方法能够有效降低计算开销和存储开销。

区块链；可审计；混币服务；隐私保护

1 引言

区块链作为一种公开的账本系统，交易信息被收集并详细记录在其中，任何参与者都可以查询链上信息，故其面临严重的隐私泄露风险。为保护用户隐私，区块链提供一定的假名性，用户可以在本地，通过一系列密码学变换，自行生成与身份信息无关的随机地址。这类随机地址（或假名）通常作为交易输入和输出的账号，虽然与传统账号相比，具有较好的匿名性，但只能提供有限的隐私保护。攻击者通过跟踪和分析区块链交易，配合地址ID、IP信息等可以追查到账户和交易的关联性，进而推测出交易隐私和身份隐私。例如，Dorit等[1]通过分析比特币的历史账本，得出相关交易之间的许多统计特征。Reid等[2]证明多个假名地址可以链接到单个用户地址。Koshy等[3]介绍了将比特币地址直接映射到IP地址的方法。Miller等[4]公布了一种发现比特币网络拓扑以及关键节点的技术AddressProbe。和传统领域不同，区块链上记录的信息不可删除和篡改，敏感信息一旦泄露，无法挽救，因此，区块链系统应该更加重视隐私防护问题，同时迫切需要为区块链用户提供完整的隐私保护服务。

一种直观的区块链隐私保护方法被称为混币。混币是在不改变交易结果的前提下，通过对交易内容进行混淆，从而增加攻击难度的隐私保护方法。2013年，Maxwell等[5]提出第一个混币方案CoinJoin，通过割裂输入地址和输出地址的联系，达到保护用户交易隐私的目的。2014年，Bonneau等[6]提出一种改进的混币方案Mixcoin，增加审计功能，监管混币服务器的行为，防止混币服务器违规操作。2015年，Valenta等[7]在Mixcoin的基础上，提出一种采用盲签名技术的方案Blindcoin，以防止混币服务器泄露混币地址的链接关系。2016年，Heilman等[8]采用盲签名和智能合约技术，通过智能合约提供可自动强制执行的协议，能同时为链上区块链交易和链下区块链交易提供匿名保护。2018年，Bao等[9]在Blindcoin的基础之上，利用多签名技术对混币方案进一步优化，他们设计的Lockcoin方案不仅能够防止混币服务器建立输入地址和输出地址间的映射关系，而且能够预防混币服务器篡改输出地址来盗窃用户资金。

在早期的混币方案中，如CoinJoin[5]和Mixcoin[6]方案，为正确完成混币操作且输出到相应的用户地址，混币服务器了解全部的混币信息，用户的输入地址和输出地址对于混币服务器而言是透明的，存在严重的隐私泄露风险。为防御这类隐私泄露风险，研究者提出采用盲签名技术的改进方案，确保混币服务器在正常提供混淆服务的同时，无法建立输入和输出地址之间的关联性，如Blindcoin[7]、Lockcoin[9]、RSA-Coinmix[10]方案。这些采用盲签名技术的方案能够有效抵御混币器泄露区块链用户隐私的风险，但存在计算和存储开销较大的问题。例如，Blindcoin和Heilman采用基于双线性对（bilinear pairing）的盲签名方案，RSA-Coinmix和Lockcoin则采用基于RSA算法的盲签名方案。基于双线性对问题构造的签名单位安全强度高，同等安全强度下，所需密钥长度短，但双线性对运算计算开销较大。而RSA算法基于大整数因子分解问题，基于RSA算法构造的签名计算开销较小，但签名的单位安全强度较低，同等安全强度下，所需密钥长度较长，存储开销较大。目前，计算和存储开销是限制区块链发展的瓶颈，因此在满足安全强度的条件下，需要设计更高效节能的盲签名方案。此外，混币服务器存在盗窃资金的风险，而用户也存在拖延支付的可能，任何一方的违规操作，都会造成安全性和执行效率下降，因此，需要设计可审计的混币协议来同时监管混币器和用户两方的行为，确保混币服务的安全高效。

本文首先在Blindcoin[7]方案的基础之上，设计了包含用户、混币器、审计区块链三类实体的混币服务系统模型；其次，利用仿射变换构造盲签名的方法，将Schnorr盲签名方案在椭圆曲线上进行模拟，并采用3个随机盲化参数，构造基于椭圆曲线的Schnorr强盲签名方案；最后，在混币服务系统模型下，应用所构造的Schnorr强盲签名方案，并采用经济惩罚机制和公共日志审计措施，提出了高效安全的可审计盲混币服务协议。

2 背景

2.1 区块链的隐私需求

为了保护用户隐私，区块链需要满足以下要求：①交易之间的链接关系式不可见或不可被分析；②交易内容仅对实际参与者可见。对于私有链或许可链而言，通过设置访问控制策略，可以增加非法节点进入区块链系统的难度，降低数据透明度，从而提升隐私防护能力。但是，区块链中的节点通常是个人计算机或手机，安全防护能力低，容易遭受攻击者的攻击。此外，在公有链场景下，每个用户都可以自由地访问区块链系统，能够查看并下载全局账本信息，存在极大的隐私泄露风险。为抵御风险，文献[11]将区块链的隐私需求划分为身份隐私和交易隐私两方面。

身份隐私指区块链中的用户信息（包括地址信息和交易内容）和用户真实身份之间的映射关系。在区块链中，用户可以在本地通过一系列密码学变换，自行生成与身份信息无关的随机地址。该地址通常作为交易输入和输出的账号，虽然与传统账号相比，具有较好的匿名性，但这类随机地址（或假名）只能提供有限的身份隐私保护。当用户通过随机地址参与区块链交易时，攻击者通过遍历账本信息，分析区块链交易的网络传播规律[12]，配合使用一些行为分析策略[13]，能够推测出区块链用户的真实身份信息。

交易隐私指区块链交易内容和交易内容背后的敏感信息之间的关联性。公开的交易记录能够反映一些敏感信息，如用户的购买记录，能够反映用户的消费水平和购买喜好。此外，在许多基于区块链的应用中，如电子医疗记录管理[14]、匿名的身份验证和授权[15]等，区块链上存储的交易记录涉及重要的用户敏感信息。和传统领域不同，区块链上记录的信息不可删除和篡改，敏感信息一旦泄露就无法挽救，因此区块链系统应该更加重视隐私防护问题。

为提高区块链系统隐私防护的能力，理想的解决方案应该包括以下几种特征。

1) 匿名性：用户是唯一知道输入地址和输出地址链接关系的实体。

2) 可扩展性：该系统具备良好的可扩展性，能容纳多个用户。

3) 兼容性：该系统能够兼容现有的区块链系统，如比特币、以太坊。

4) 可审计性（仅限混币服务）：当协议无法正常执行时，参与混币的双方都能获取错误操作的证据。

2.2 混币服务

在区块链中，交易的输入地址和输出地址是可链接的，通过分析公开账本的内容，能够推断出一些隐私信息。针对此类攻击，一种直观的防护方案是借助中间混币器来混淆交易地址的关系。1981年，Chaum首次提出混币服务的思想[16]，起初的目的是通过混币器来隐藏参与者的通信内容，从而实现匿名通信。混币服务的基本思想可表达为

文献[13]介绍了混币服务的基础架构，如图1所示，多个输入经中间混币服务器执行混淆操作后依次输出，为了隐藏输入到达的顺序，混币器将通过随机排序的方式打乱输出顺序。此外，为尽可能减小单个混币器受攻击的风险，可以将多个混币器连接在一起，构成级联混币器，提升防护能力。

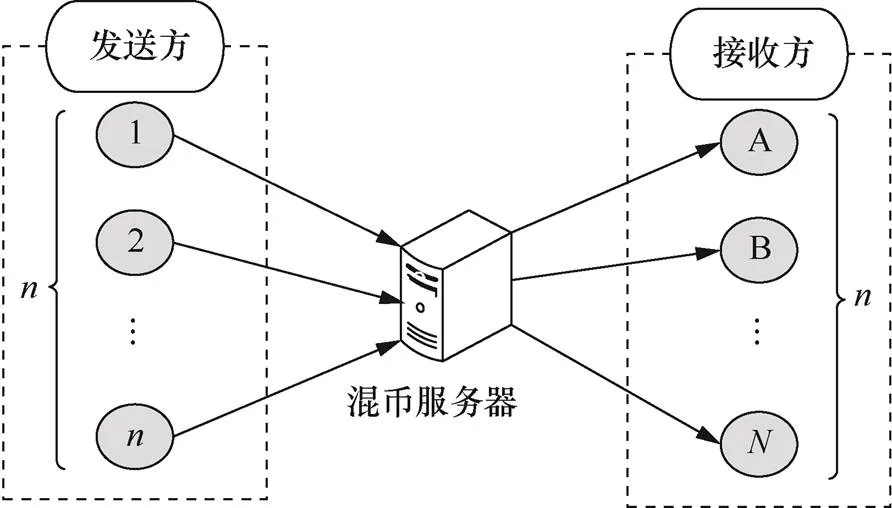
图1 混币服务的基础架构

Figure 1 Infrastructure of mixed-coin service

2.3 盲签名

盲签名是由Chaum[17]在1983年提出的一种数字签名方式，其通过允许文档提供者在签名者对文档不可见的情况下，获得“盲”文档签名的方式，来为实际文档内容提供隐私。由于文档内容在签名之前对签名者而言是不可见的（或盲化的），因此盲签名可有效保护签名内容，在电子选举和数字金融领域已有广泛应用[18]。文献[19]介绍了一般签名方案和盲签名方案的对比，如图2所示。在图2(a)所示的一般签名方案中，签名者根据已知的消息内容产生数字签名。与一般的签名方案相比，盲签名的过程如图2(b)所示。签名请求方对消息执行盲化操作，并将盲消息发送给签名者。签名者签署盲消息并将盲签名返回给请求方，然后请求方解盲签名以获得原始消息上的签名。

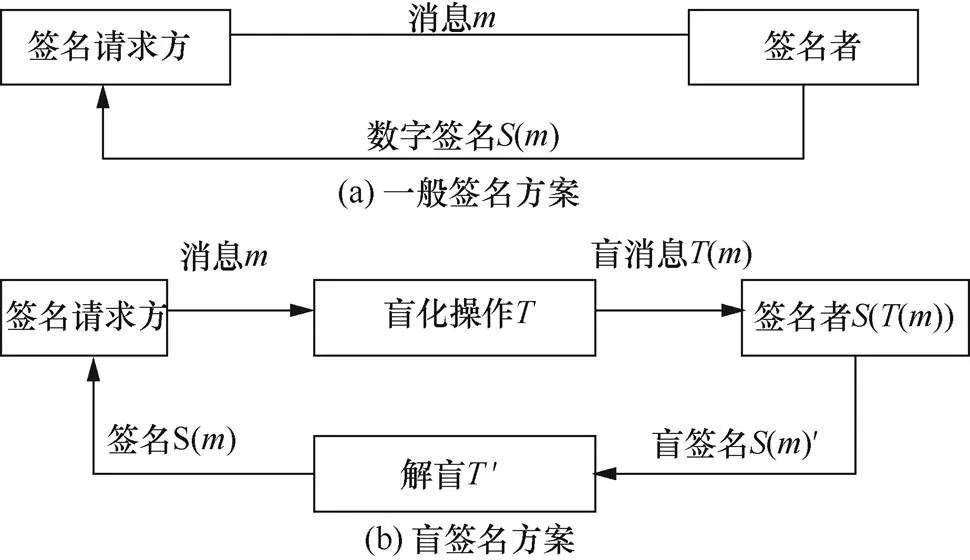
图2 一般签名方案和盲签名方案的对比

Figure 2 Comparison of general signature scheme and blind signature scheme

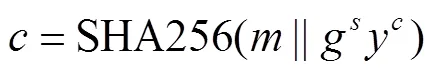
该方案有效的原因如下。

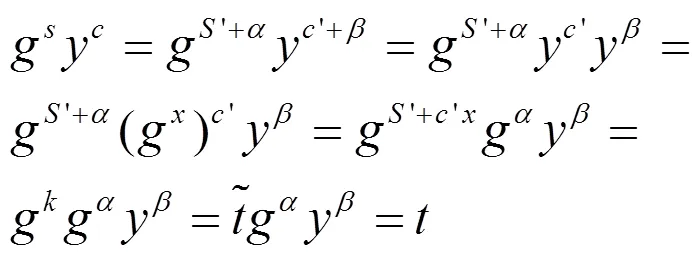
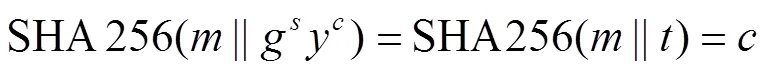
3 盲混币服务方案

3.1 盲混币服务的系统模型

在Blindcoin[7]方案的基础上，本文设计了盲混币服务的系统模型，如图3所示，该模型包含3个主要实体，分别是混币服务器（M，mixer）、用户（U，user）和审计区块链（audit blockchain）。

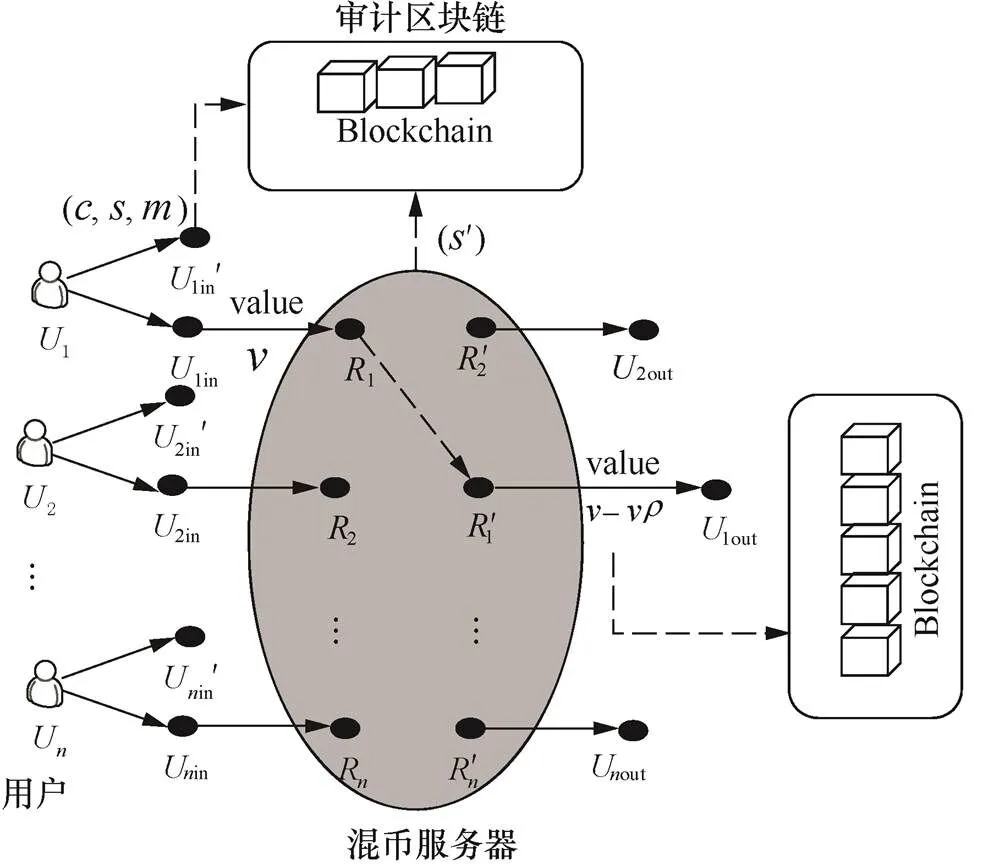
图3 盲混币服务的系统模型

Figure 3 System model of blind mixed-coin service

审计区块链：审计区块链是混币服务的监督者，可看作一块只可添加不可更改的公告板，用于第三方验证。审计区块链以区块链的形式分享信息，发送方可通过交易的方式将证据信息记录在区块链上。用户和混币器均可发布区块链消息，并且消息一经发布不可删除。如果用户和混币器中任何一方违反协议，通过审计区块链中包含的公开信息，可证明违规方的行为。

盲混币服务系统模型包含许多参数，具体如表1所示，除了模型图中涉及的参数外，还将在3.3节盲混币服务协议中被大量应用。

3.2 基于椭圆曲线的Schnorr强盲签名

表1 盲混币服务系统模型参数

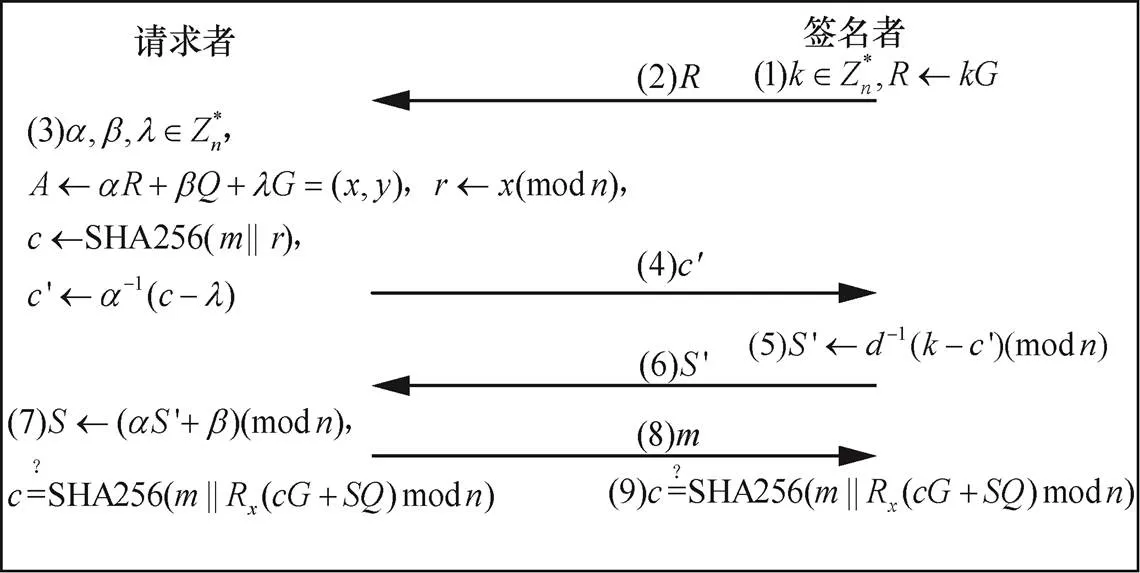
图4 Schnorr强盲签名协议

Figure 4 Schnorr strong blind signature protocol

Schnorr强盲签名协议执行步骤如下。

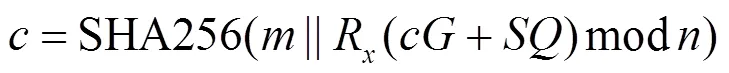
可用性证明如下。

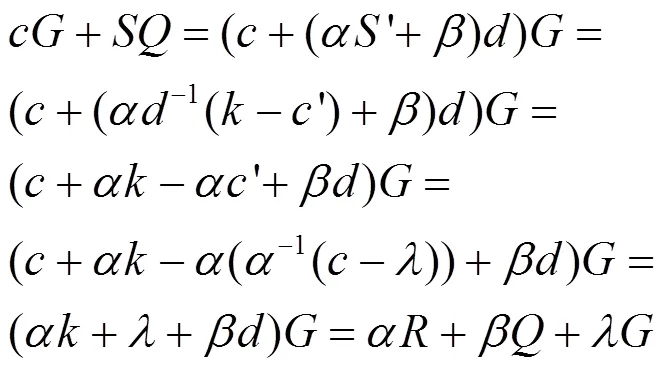
一般来说，不可伪造性、不可抵赖性、盲性、不可跟踪性4条性质既是设计盲签名所遵循的标准，也是判断盲签名安全性的依据。因此，以这4条性质为标准，对基于椭圆曲线的Schnorr强盲签名方案进行安全分析，该方案具有以下安全特性。

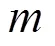
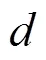
3.3 可审计的盲混币服务协议

本节介绍可审计的盲混币服务协议，该协议是在3.1节介绍的盲混币服务系统模型下，应用3.2节提出的基于椭圆曲线的Schnorr强盲签名方案，并采用经济惩罚机制和审计措施，设计的一种高效安全的服务协议。经济惩罚机制指利用博弈论的思想，通过经济奖惩来制约混币服务器和用户双方的行为。一方面，针对混币服务器，在混币服务器提供混币服务之前，要求混币服务器预置大额诚信押金（远超单次混币金额）作为信用担保。若混币服务器正常提供服务，则在每次混币服务后可获取相应奖励，并且诚信押金可赎回，若混币服务器执行违规操作，故意延迟或者盗用资金，一经核实，诚信押金将被全部罚没。另一方面，针对用户，混币服务之前用户将混币资金转移到混币服务器，若正常执行流程，则完成混币需求，若故意延迟或恶意发起申请（DoS攻击），一经核实，混币资金将被罚没作为混币服务器的费用。为最大化收益，混币服务器和用户都会遵守协议规则，确保协议的正常执行。审计措施指利用审计区块链不可篡改的特性，记录混币服务器和用户的混币信息，作为审核其行为的可信证据。与现有的方案相比，本文提出的可审计盲混币服务协议，主要的特点是高效性，通过应用基于椭圆曲线的Schnorr强盲签名，降低了签名过程的存储开销和计算开销。可审计盲混币服务协议流程如图5所示。

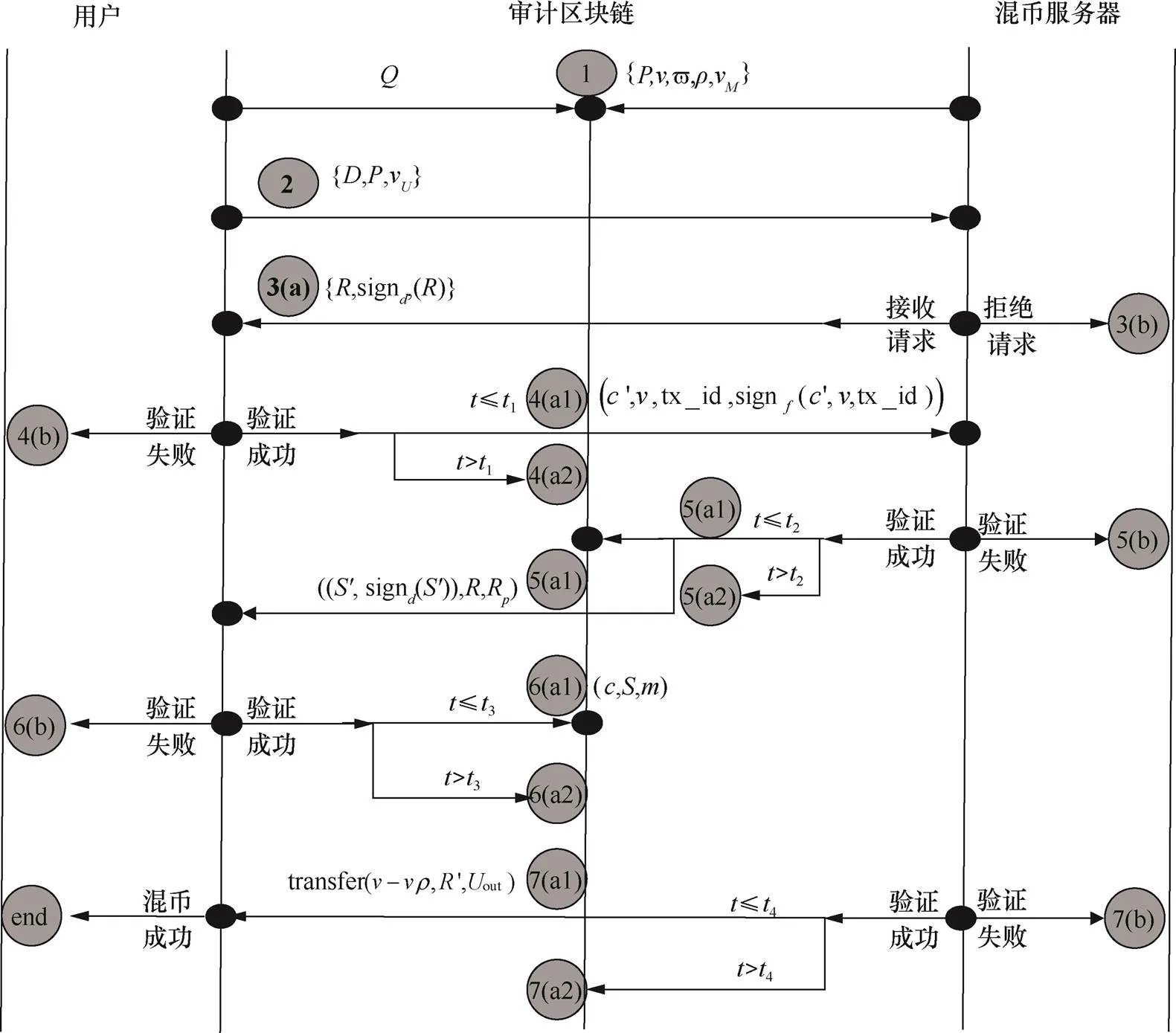
图5 可审计的盲混币服务协议

Figure 5 Auditable blind mixed-coin service protocol

可审计的盲混币服务协议过程具体步骤如下。

Step1 系统初始化。

Step2 混币服务请求。

Step3(a) 托管地址分发。

Step3(b) 混币服务拒绝。

Step4(a1) 盲化。

Step4(b) 验证。

Step5(a1) 盲签名。

Step5(b) 验证。

Step6(a1) 解盲。

Step6(b) 验证。

Step7(a1) 混币服务完成。

Step7(b) 验证。

4 实验与分析

4.1 强盲签名算法的有效性验证

强盲签名算法实现流程如图6所示，主要包括获取全局参数、生成公钥和私钥、获取随机数和盲化因子、盲化、盲签名、解盲、验证这7个流程。

盲签名算法的有效性验证实验在配置为Intel Core i3-3110M @2.40 GHz CPU和4 GB内存的计算机上进行，操作系统为64位Windows7系统。在Eclipse平台上用Java语言编程实现基于椭圆曲线的Schnorr强盲签名算法，算法实现如图7所示。

实验表明，经过盲化、盲签名、解盲、验证后，得到结果为true，说明本文设计的基于椭圆曲线的Schnorr强盲签名算法是可行有效的。

4.2 盲混币服务方案的性能分析

盲混币服务方案的性能分析包括盲签名方案的效率分析和混币服务的开销分析两方面。下面介绍盲签名方案的效率分析，盲签名算法主要分为密钥生成、盲化、盲签名、解盲和验证5个步骤，每个步骤都会产生计算开销和存储开销。计算开销以计算时间来衡量，存储开销以密钥长度和盲签名长度来衡量。为保证安全强度，本文设计的基于椭圆曲线的Schnorr强盲签名方案采用256位密钥长度。为评估本文盲签名算法的计算效率，以程序运行时间作为计算时间的实验统计值，在4.1节实验条件下，分别取用户数目为10、100、500、1 000、3 000、5 000、7 000、10 000进行测试，每次测试重复10次取均值，统计各步骤的运行时间，统计结果如表2所示。

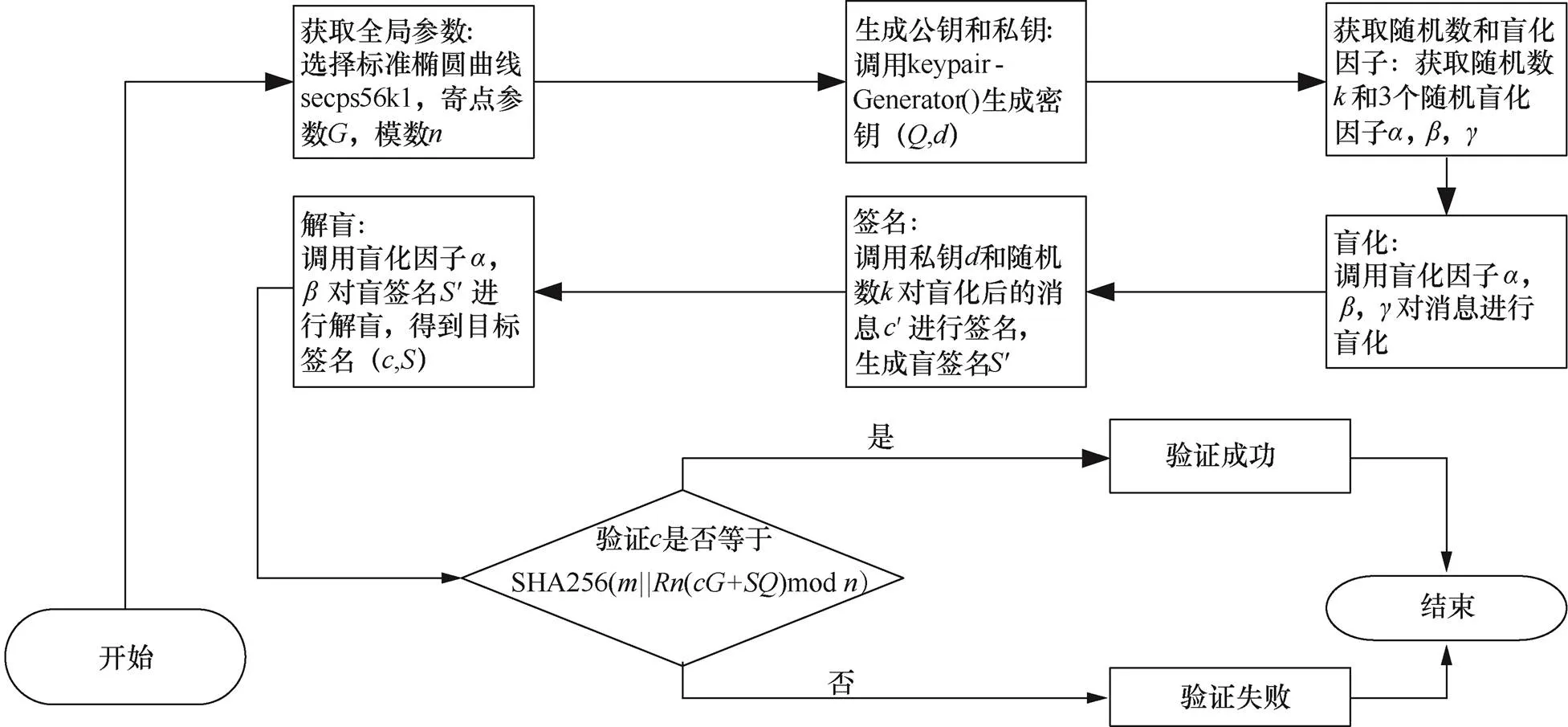
图6 强盲签名算法实现流程

Figure 6 Strong blind signature algorithm implementation process

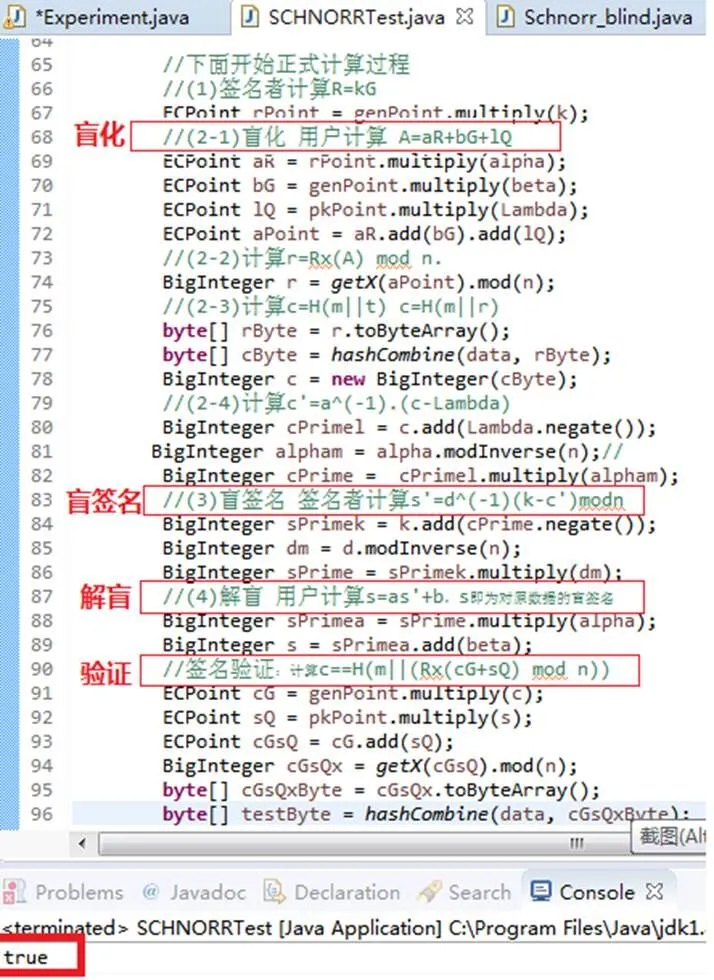
图7 强盲签名的算法实现

Figure 7 Algorithm implementation of strong blind signature

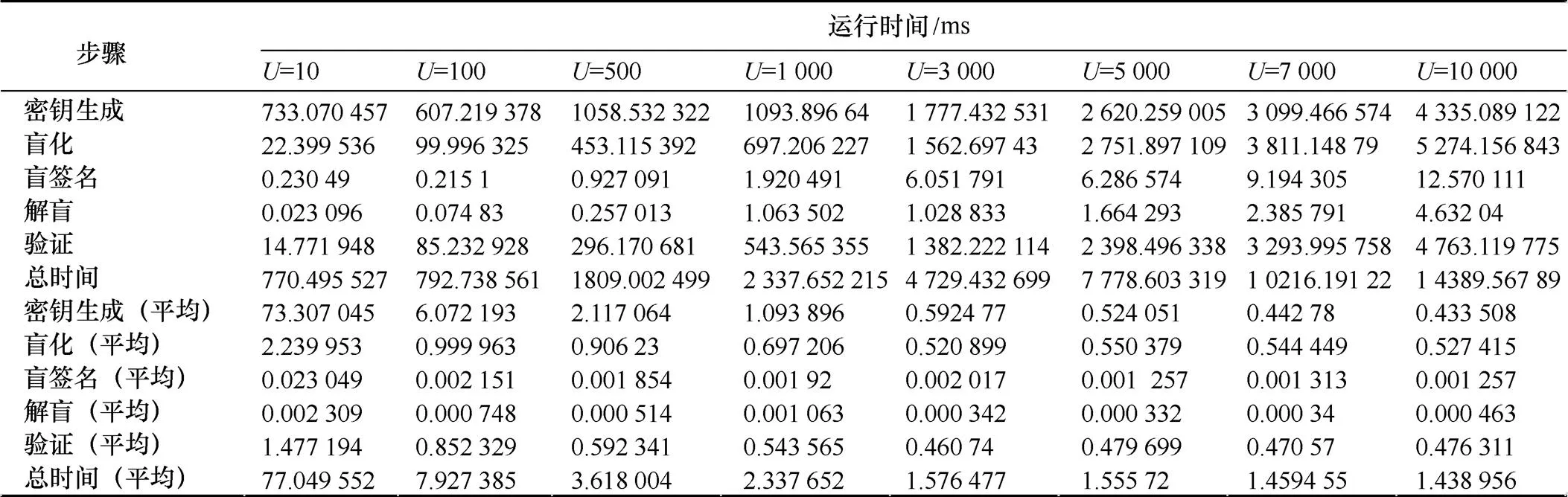
表2 盲签名方案的计算开销统计

从表2的统计结果可以看出各步骤运行时间和用户数目的关系，为更直观展示其中的关系变化和趋势，通过Matlab绘制分析图，结果如图8、图9所示。图8展示了运行时间占比和用户数目的关系，当用户数低于500时，密钥生成的运行时间占比最大，超过0.5，随着用户数目的增加，密钥生成的运行时间占比逐渐减少，而盲化和验证过程的运行时间占比逐渐增加，当用户数超过7 000时，密钥生成、盲化和验证的运行时间占比趋于稳定，都为0.3左右。图9(a)展示了运行总时间和用户数目的关系，随着用户数目的增加，总的运行时间逐渐增加，大致呈线性趋势；图9(b)展示了平均运行总时间和用户数目的关系，随着用户数目的增加，平均每个用户的运行时间逐渐减少，且当用户数大于1 000以后，平均每个用户的运行时间趋于稳定。图8、图9的结果说明本文盲签名方案具有一定的可扩展性，能够支持大规模的用户请求。

图8 运行时间占比和用户数目的关系

Figure 8 The relationship between the proportion of running time and the number of users

为进一步评估盲签名方案的效率，选择采用基于双线性对盲签名的Heilman[8]方案和基于RSA算法盲签名的RSA-Mixing[10]方案作为对比，对比结果如表3所示。

本文的盲签名算法是基于椭圆曲线上的离散对数问题构造签名密钥，Heilman[8]方案是基于椭圆曲线上的双线性对问题构造密钥，而双线性对问题是依赖群上的离散对数问题，因此，本质上本文方案和Heilman[8]方案都基于椭圆曲线上的离散对数问题构造签名密钥。RSA-Mixing[10]方案则基于大整数因子分解问题构造密钥。因为基于椭圆曲线上的离散对数问题构造的签名单位安全强度高于基于大整数因子分解问题构造的签名，所以在提供同等安全强度时，前者所需密钥长度更短。在本文的对比实验中，本文方案和Heilman[8]方案选择256 bit的密钥长度，RSA-Mixing[10]方案则选择1 024 bit密钥长度。

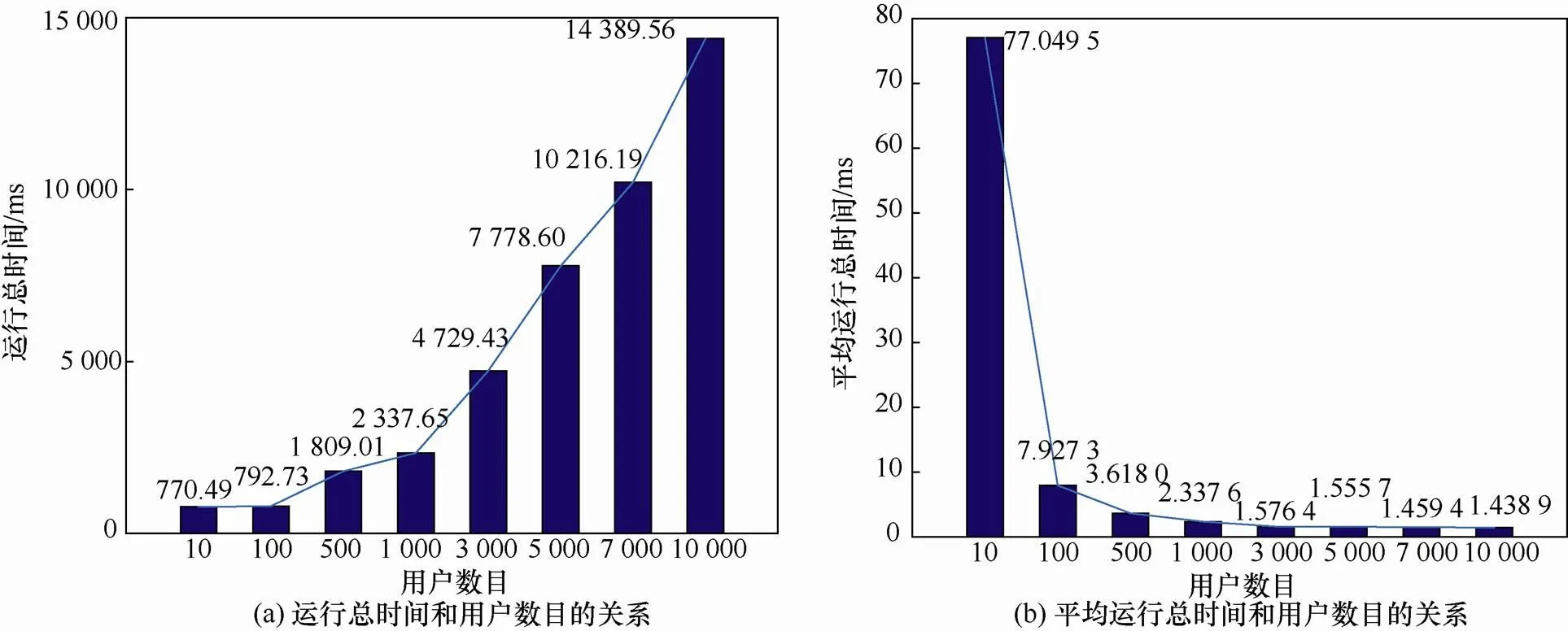
图9 运行总时间和用户数目的关系

Figure 9 The relationship between the total running time and the number of users requested

表3 盲签名方案的算法运算过程

取=1 000，代表10 000个用户请求盲签名，在4.1节实验条件下，分别部署3个盲签名算法，每次实验重复10次取均值，得出的对比结果如图10所示。

从对比结果可以看出，RSA-Mixing[10]方案计算时间最长，且耗时集中在密钥生成阶段，这是因为该方案基于大整数因子分解问题，签名的单位安全强度较低，同等安全强度下，所需的密钥长度最长，而密钥长度的增加会导致加解密速度大大降低；Heilman[8]方案和本文方案计算时间较少，且耗时主要在盲化、盲签名和验证阶段，其中盲化和盲签名阶段两方案耗时相近，验证阶段Heilman[8]耗时约为本文方案的10倍，这是由于在验证阶段，Heilman[8]方案中双线对运算的计算量较大。此外，Heilman[8]方案和本文方案的签名单位安全强度较高，同等安全强度下，所需的密钥长度较短，因此存储开销小于RSA-Mixing[10]方案。

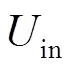
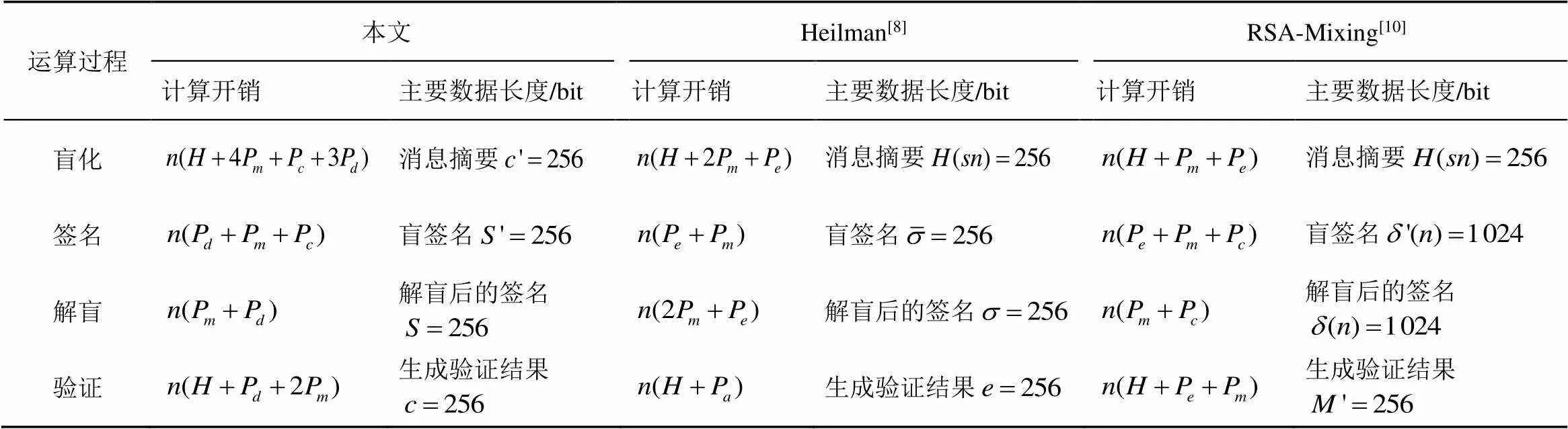
表4 计算和存储开销的量化比较

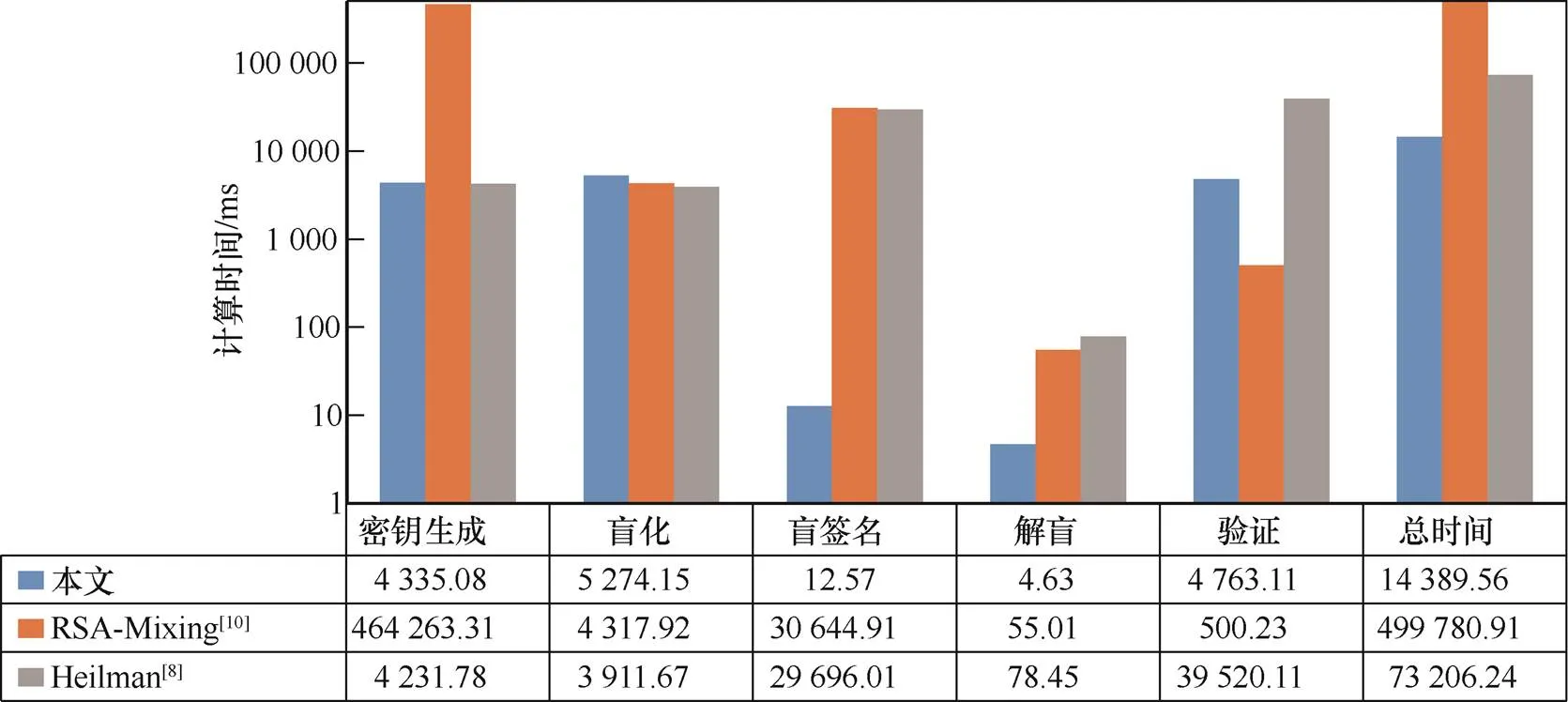
图10 各盲签名方案计算时间对比

Figure 10 Comparison of computing time of each blind signature scheme

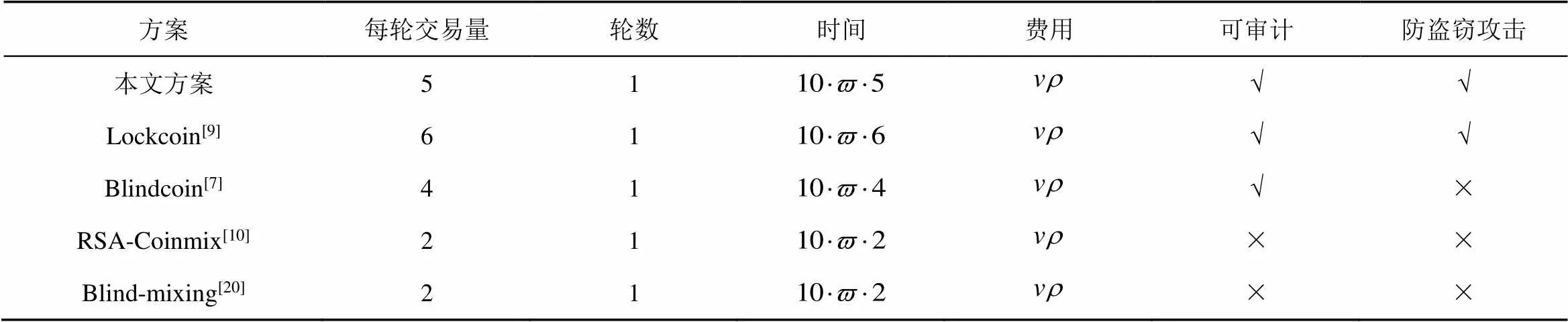
表5 混币服务开销对比

表5中所列方案都是基于盲签名的混币服务方案，在所有对比方案中，RSA-Coinmix[10]和Blind-mixing[19]时间开销最少，但不可审计，也不能防止盗窃攻击，安全性较低。Lockcoin[9]、Blindcoin[7]和本文方案都具有可审计性，且Blindcoin[7]时间开销最少，但Blindcoin[7]不能防止盗窃攻击，存在风险。Lockcoin[9]和本文方案都具有可审计性，也能防止盗窃攻击，但本文方案的时间开销更低，效率更高。此外，所有对比方案的混币费用开销相同。

4.3 混币服务方案的特性分析

以理想的区块链隐私匿名解决方案为衡量标准，讨论本文所提可审计盲混币服务方案，分析其具有的特性，包括匿名性、防DoS攻击、防盗窃攻击、可审计性、可扩展性和兼容性。

匿名性：混币服务协议最重要的特性是匿名性，而匿名程度则以不可链接性和不可追踪性来衡量。

（1）不可追踪性

（2）不可链接性

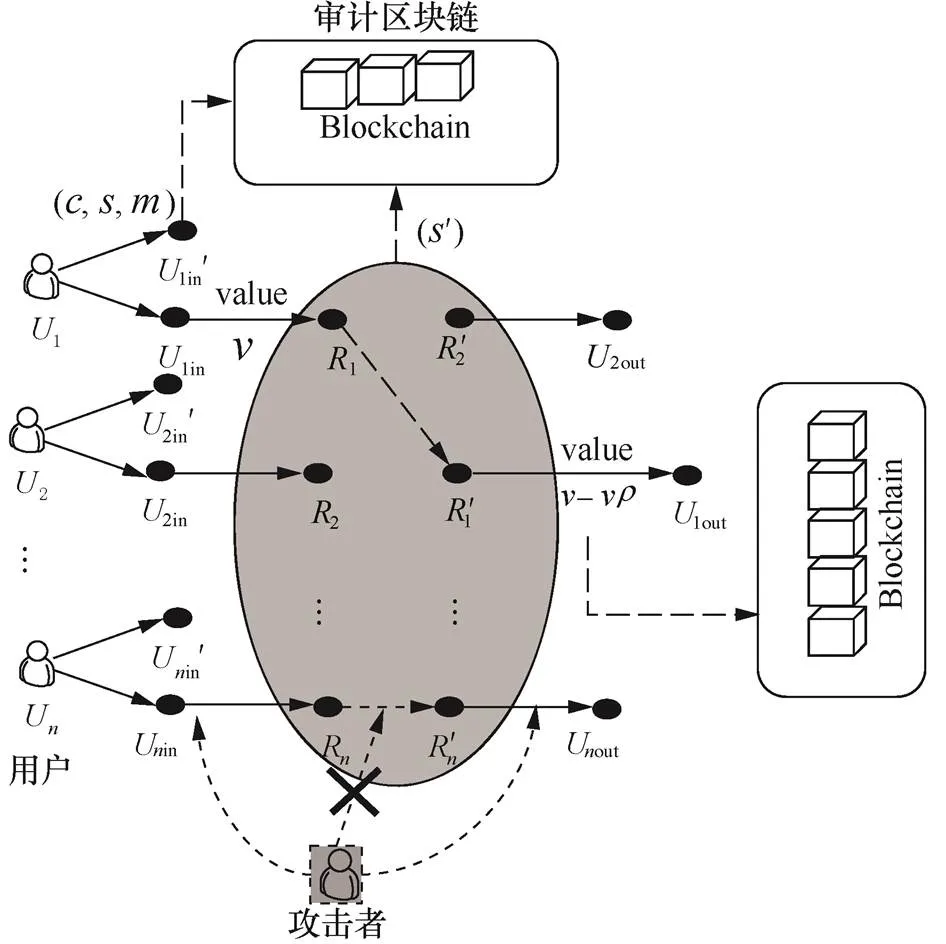
图11 追踪攻击分析

Figure 11 Tracking attack analysis

防DoS攻击：在许多分布式混币协议中，攻击者进行DoS攻击主要通过用户参与协议到一定程度后，拒绝转移资金，导致操作失败。在本文方案中，每个用户只与混币器交互，拒绝遵守协议，不影响其他用户或减慢混币过程。攻击者还可以尝试通过阻止资金交易和审计区块链信息上链的方式，来进行DoS攻击。但这种方式是很难实际操作的，因为攻击者很难控制大部分的矿池算力。此外，由于参与混币服务需要收取费用，针对混币器发动DoS攻击，会给攻击者带来巨大的经济负担。

防盗窃攻击：由于混币服务器支付了远超过单次混币金额的押金，且协议中包含可审计的问责机制，混币器违规盗用混币资金将得不偿失，从经济角度防止服务器盗窃混币资金。

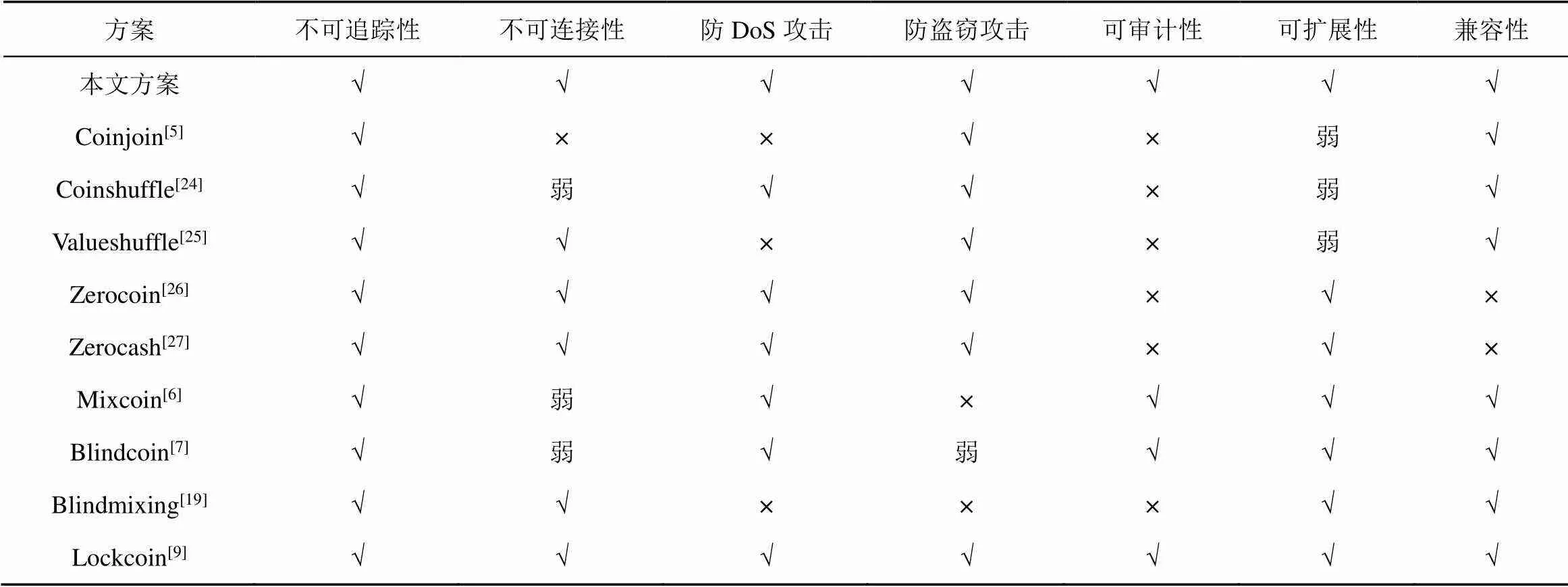
表6 不同方案的特性比较

可审计性：本文方案中使用审计区块链作为审计日志，用户和混币服务器都需要遵守协议，在规定的时间，执行相应步骤。当某一方违反协议时，第3.3节中的步骤5(a2)、步骤6(a2)、步骤7(a2)可以确保协议被正确问责。

可扩展性：与Blindcoin[7]方案相似，混币服务器可支撑扩展到更多用户，因为用户只与中心混币器交互，而不与彼此交互。此外，如果一个服务器达到瓶颈，则可以将混币功能负载到几个不同服务器上，所有的服务器均使用相同的加密密钥进行操作。

兼容性：本文方案的混币协议可作为区块链的一种服务，与现有区块链系统兼容性高，如比特币系统。

文献[23]讨论了主流的混币服务方案具备的特性，本文选取了其中几种典型方案[5-7,24-25]作为比较。此外，虽然在文献[23]中未讨论，但是比较典型[26-27]和新颖[9-10]的方案，本文也列出一并进行比较，结果如表6所示。

从对比结果可知，与其余方案相比，Zerocoin[26]、Zerocash[27]、Lockcoin[9]和本文方案具有不可追踪性、不可连接性、防DoS攻击、防盗窃攻击4项安全特性，具备更高的安全防护能力；而Zerocoin[26]和Zerocash[27]缺少可审计性和兼容性，存在问责困难和部署复杂的问题，Lockcoin[9]和本文方案则具有全部的6项特性；由4.2节混币服务开销分析可知，相较于Lockcoin[9]，本文方案开销更低，效率更高。

5 结束语

本文介绍了一种高效安全保护隐私的混币服务方案。该方案不仅能割裂输入地址和输出地址的链接，实现隐私保护的目的，具备较低的计算和存储开销，并且拥有良好的安全特性，包括匿名性、防DoS攻击、防盗窃攻击、可审计性等。虽然所提方案具有较高的效率和安全性，但在等待交易的确定过程中，由于采用了工作量证明共识机制，存在交易时延较大的问题，未来可以继续开展对共识机制的优化研究，以提升执行效率。

[1] DORIT R, SHAMIR A. Quantitative analysis of the full bitcoin transaction graph[C]//International Conference on Financial Cryptography and Data Security. 2013: 6-24.

[2] REID F, HARRIGAN M. An analysis of anonymity in the bitcoin system[M]//Security and privacy in social networks. 2013: 197-223.

[3] KOSHY P, KOSHY D, MCDANIEL P. An analysis of anonymity in bitcoin using P2P network traffic[C]//International Conference on Financial Cryptography and Data Security. 2014: 469-485.

[4] MILLER A, LITTON J, PACHULSKI A, et al. Discovering bitcoin’s public topology and influential nodes[R]. 2015.

[5] MAXWELL G. CoinJoin: bitcoin privacy for the real world[C]// Post on Bitcoin Forum. 2013.

[6] BONNEAU J, NARAYANAN A, MILLER A, ET al. Mixcoin: anonymity for bitcoin with accountable mixes[C]//International Conference on Financial Cryptography and Data Security. 2014: 486-504.

[7] VALENTA L, ROWAN B. Blindcoin: blinded, accountable mixes for bitcoin[C]//International Conference on Financial Cryptography and Data Security. 2015: 112-126.

[8] HEILMAN E, BALDIMTSI F, GOLDBERG S. Blindly signed contracts: anonymous on-blockchain and off-blockchain bitcoin transactions[C]//International Conference on Financial Cryptography and Data Security. 2016: 43-60.

[9] BAO Z, WANG B, ZHANG Y, et al. Lockcoin: a secure and privacy-preserving mix service for bitcoin anonymity[J]. International Journal of Information Security, 2018, 19(3): 311-321.

[10] 吴文栋. 基于盲签名技术的比特币混币系统设计与实现[D]. 深圳: 深圳大学, 2015.

WU W D. Bitcoin mix system design based on partial blind signature[D]. Shenzhen: Shenzhen University, 2015.

[11] FENG Q, HE D, ZEADALLY S, et al. A survey on privacy protection in blockchain system[J]. Journal of Network and Computer Applications, 2019, 126: 45-58.

[12] BIRYUKOV A, KHOVRATOVICH D, PUSTOGAROV I. Deanonymisation of clients in Bitcoin P2P network[C]//Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security. 2014: 15-29.

[13] SCHOTT P A. Reference guide to anti-money laundering and combating the financing of terrorism[M]. The World Bank, 2006.

[14] DUBOVITSKAYA A, XU Z, RYU S, et al. Secure and trustable electronic medical records sharing using blockchain[C]//AMIA Annual Symposium Proceedings. American Medical Informatics Association. 2017: 650.

[15] YAO Y, CHANG X, MIŠĆ J, et al. BLA: blockchain-assisted lightweight anonymous authentication for distributed vehicular fog services[J]. IEEE Internet of Things Journal, 2019: 3775-3784.

[16] CHAUM D L. Untraceable electronic mail, return addresses, and digital pseudonyms[J]. Communications of the ACM, 1981, 24(2): 84-90.

[17] CHAUM D. Blind signatures for untraceable payments[C]//Advances in Cryptology. 1983: 199-203.

[18] ISLAM S K H, AMIN R, BISWAS G P, et al. Provably secure pairing-free identity-based partially blind signature scheme and its application in online e-cash system[J]. Arabian Journal for Science and Engineering, 2016, 41(8): 3163-3176.

[19] SHENTU Q C, YU J P. A blind-mixing scheme for Bitcoin based on an elliptic curve cryptography blind digital signature algorithm[J].Computer Science, 2015.

[20] CAMENISCH J L, PIVETEAU J M, STADLER M A. Blind signatures based on the discrete logarithm problem[C]//Workshop on the Theory and Application of of Cryptographic Techniques. 1994: 428-432.

[21] DINGLEDINE R, MATHEWSON N, SYVERSON P. Tor: the second-generation onion router[J]. Journal of the Franklin Institute, 2004, 239(2):135-139.

[22] 王化群, 张力军, 赵君喜. 基于椭圆曲线的Schnorr盲签名[J]. 计算机工程与设计, 2005, 26(007):1819-1822.WANG H Q, ZHANG L J, ZHAO J X. Schnorr blind signature based on elliptic curve[J]. Computer Engineering and Design, 2005, 26(7): 1819-1822.

[23] CONTI M, KUMAR E S, LAL C, et al. A survey on security and privacy issues of bitcoin[J]. IEEE Communications Surveys & Tutorials, 2018, 20(4): 3416-3452.

[24] RUFFING T, MORENO-SANCHEZ P, KATE A. Coinshuffle: Practical decentralized coin mixing for bitcoin[C]//European Symposium on Research in Computer Security. 2014: 345-364.

[25] RUFFING T, MORENO-SANCHEZ P. ValueShuffle: mixing confidential transactions for comprehensive transaction privacy in bitcoin[C]//International Conference on Financial Cryptography and Data Security. 2017: 133-154.

[26] MIERS I, GARMAN C, GREEN M, et al. Zerocoin: Anonymous distributed e-cash from bitcoin[C]//2013 IEEE Symposium on Security and Privacy. 2013: 397-411.

[27] SASSON E B, CHIESA A, GARMAN C, et al. Zerocash: Decentralized anonymous payments from bitcoin[C]//2014 IEEE Symposium on Security and Privacy. 2014: 459-474.

Efficient and safe auditable mixed-coin service scheme based on blind signature

QIAO Kang, TANG Hongbo, YOU Wei, LI Haitao

Information Engineering University, Zhengzhou 450001, China

The mixed-coin service can provide solutions for the privacy problem of blockchain, but it still faces efficiency bottlenecks and security risks. To further improve the efficiency and security protection of the mixed-coin service, an efficient and safe auditable mixed-coin service scheme based on blind signature was proposed. Firstly, this scheme added audit measures. It added an audit blockchain to the traditional mix-coin model to record the behavior of users and mixers, achieving traceability and accountability. Then, this method used elliptic curves algorithm to construct blind signatures instead of blind signature schemes based on bilinear pairs or RSA. Finally, this scheme proposed an auditable blind mix-coin service agreement based on the auditable mix-coin model and the blind signature algorithm based on elliptic curve.Simulation analysis shows that the proposed scheme has six security features, such as auditability and anti-theft attack, while providing privacy protection. Under the same security intensity, the proposed scheme can effectively reduce the computational overhead and storage overhead.

blockchain, auditable, mixed-coin, privacy protection

s: The National Key R&D Program Cyberspace Special (2016YFB0801605), The National Natural Science Foundation Innovation Group Project (61521003), The National Natural Science Foundation of China (61801515)

TP399

A

10.11959/j.issn.2096−109x.2020043

乔康（1994− ），男，四川邛崃人，信息工程大学硕士生，主要研究方向为移动通信网络安全和区块链技术。

汤红波（1968− ），男，湖北孝感人，信息工程大学教授、博士生导师，主要研究方向为移动通信网络、新型网络体系结构。

游伟（1984−），男，江西丰城人，博士，信息工程大学讲师，主要研究方向为密码学和移动通信网络。

李海涛（1982− ），男，山东泰安人，信息工程大学讲师，主要主要研究方向为网络数据挖掘。

论文引用格式：乔康, 汤洪波, 游伟, 等. 高效安全的可审计盲混币服务方案[J]. 网络与信息安全学报, 2020, 6(4): 23-36.

QIAO K, TANG H B, YOU W, et al. Efficient and safe auditable mixed-coin service scheme based on blind signature[J]. Chinese Journal of Network and Information Security, 2020, 6(4): 23-36.

2020−01−07；

2020−04−03

乔康，773441271@qq.com

国家重点研发计划网络空间专项（2016YFB0801605）；国家自然科学基金创新群体项目（61521003）；国家自然科学基金（61801515）