考虑驱动带的客车悬置系统振动分析及设计

李智强，张攀登

考虑驱动带的客车悬置系统振动分析及设计

李智强1，张攀登2

（1.福建船政交通职业学院 汽车系，福建 福州 350007；2. 同济大学 机械与能源工程学院，上海 200092）

为了研究客车发动机前端驱动带对动力总成悬置系统振动特性和隔振设计的影响，建立了考虑驱动带的悬置系统模型，对悬置系统的固有特性进行了计算；通过对比不考虑驱动带模型的计算和驱动带刚度的设计研究，分析了驱动带对悬置系统振动特性的影响。以悬置安装位置和角度为设计变量建立优化设计模型，采用遗传算法对不考虑驱动带和考虑驱动带两种方式建立的模型进行优化设计，对优化结果进行了比较分析。此外，通过对动力总成施加发动机激励，对比研究两种建模方法优化前后振动响应的情况，表明考虑驱动带的模型在优化后悬置元件向车身的传递力响应最小，设计效果比不考虑驱动带要好。

振动；客车；动力总成悬置系统；建模；驱动带，设计

汽车动力总成悬置系统是由动力总成、悬置元件及安装支架和车架构成的系统。动力总成悬置系统除了满足基本的支撑作用外，还需要有良好的隔振性能，隔离发动机振动向车身的传递，保证良好的乘坐舒适性[1]。动力总成悬置系统的设计先建立六自由度模型，在此基础上对系统的频率、解耦率等固有特性进行分析和优化，该方法在乘用车有较成熟的应用[2-3]。对于客车动力总成悬置系统的设计，目前主要沿用乘用车的建模设计方法[4-5]。然而，客车发动机前端有驱动皮带，驱动带一端连接曲轴皮带轮，另一端连接安装在车架上的空调压缩机皮带轮和冷却风扇皮带轮，结构上与轿车存在一定的差异。针对客车驱动皮带的问题，清华大学王亚楠、吕振华曾开展相关工作，研究了几种弹性参数对动力总成悬置系统的影响[6]，通过调整驱动带刚度大小计算分析了系统模态频率的变化，提出设计时选用小刚度驱动带的建议[7]，但驱动带刚度与传动功率相关，选用小刚度的驱动带目前依然难以实现。

为此，建立包含驱动带的动力总成悬置系统物理和数学模型，并与不考虑驱动带建模的悬置系统进行对比研究；同时，建立优化设计方案，在同一优化设计条件下对两种建模方法的设计结果进行对比研究，并通过振动响应验证优化设计的效果。

1 悬置系统建模与振动分析

1.1 动力总成悬置系统模型

目前广泛使用的动力总成悬置系统六自由度模型，物理建模时将附件进行必要的简化，动力总成和车架视作刚体，橡胶悬置根据其特性，忽略自身重量，并抽象为具有3根互相垂直的弹性主轴元件，动力学模型为3个正交的弹簧阻尼器[8]，如图1所示。

图1 动力总成悬置系统模型

图2 发动机前端驱动带安装示意图

客车发动机前端通常带有曲轴皮带轮，通过皮带驱动空调压缩机和冷却风扇，如图2所示；或者只驱动空调压缩机，采用电子风扇。鉴于对动力总成设计的普遍适用性，以同时驱动空调压缩机和冷却风扇为例。驱动冷却风扇部分通常带有一个中间过渡轮，过渡轮支架与车架刚性连接，二级传动与动力总成关联性小，在建模中忽略不计。根据皮带的特性，将皮带简化为具有一定刚度的弹簧[9]，动力总成悬置系统其他部分沿用图1中的假设条件，增加了发动机前端驱动皮带后，系统物理模型如图3所示。

图3 考虑驱动皮带的悬置系统模型

图3中，定义动力总成质心坐标系O-XYZ，坐标原点O在质心位置；X轴和Z轴分别平行于曲轴和气缸中心线，正方向如图所示；Y轴根据坐标系右手定则确定；定义悬置元件坐标系o-，o为橡胶弹性中心位置，,,坐标分别与悬置弹性主轴方向平行[4]。两条驱动皮带按一个具有两个方向主轴刚度的悬置元件处理。动力总成的自由度为空间坐标系下沿X，Y，Z方向的平动,,和绕X，Y，Z方向的转动θ，θ，θ。定义系统广义坐标:=[，，，θ，θ，θ]T。

橡胶悬置阻尼对固有特性作用较小，在计算系统振动模态时，忽略不计[10]，系统自由振动微分方程为：

式中：为系统质量矩阵，为系统刚度矩阵。

1.2 悬置系统的固有特性

根据方程（1），系统的第阶振动圆频率λ为矩阵-1的特征值，可得到频率为f=λ/2π。解耦率是评价悬置系统设计的重要指标，可通过振动能量的方法计算。当系统以第阶模态振动，第个广义坐标系振动能量占系统总能量的百分比即为解耦率，可以表示为[10]：

式中：()为质量矩阵第（）个元素，()、()分别为第阶振型的第个和第个元素。

以某型号客车为例，该车型动力总成悬置系统有4个橡胶悬置，按发动机中心线对称布置。动力总成的质量=870 kg；转动惯量和惯性积为：[J，J,J,J,J,J]=[45, 177, 160, -1.8, -0.1, 31]，单位kg·m2。弹性体刚度参数见表2。

表2 系统弹性元件动刚度参数 N/mm

根据前面建立的数学模型，在MATLAB编写程序，代入计算参数，计算得到不考虑驱动建模系统的频率和能量分布，如表3所示；考虑驱动建模系统的频率和能量分布，如表4所示。

对比表3和表4，模态频率方面，两种模型振动的模态同一阶次对应的主振型发生了变化，数值大小上也有明显差异，考虑驱动皮带的模型因为驱动皮带刚度的影响，对应阶次的频率要大于不考虑驱动皮带的模型计算结果；解耦率方面，各主振型方向的解耦率也明显不同，考虑驱动带模型的耦合程度要比不考虑驱动带模型的大。总体上无论采用那种模型的计算结果，系统的振动特性都不满意，存在相邻阶次频率过近，系统解耦率不高的问题。

表3 不考虑驱动带的系统频率和能量分布

表4 考虑驱动带的系统频率和能量分布

1.3 驱动带刚度对系统振动特性的影响

为了进一步研究驱动带对动力总成悬置系统的影响，对系统进行设计研究。驱动带刚度变化以原系统数据为基础从0到2倍的变化，系统各阶主振型方向的频率和解耦率的变化如图4、图5所示。

由图4和图5可见，随着驱动皮带刚度变化，悬置系统的频率在θ变化明显，解耦率在各方向都有较大的变化。因此，随着驱动带刚度变化，悬置系统的振动特性有较大变化。

图4 系统频率随驱动带刚度的变化

图5 系统解耦率随驱动带刚度的变化

2 考虑驱动带的悬置系统优化设计模型

2.1 设计变量

设计变量主要选取与隔振性能相关且可变的参数，包括悬置的刚度、安装位置和角度等。仅对悬置元件的刚度优化或只对位置角度的优化在一定程度上都可以达到固有频率和解耦率改善的效果。对悬置元件刚度的设计过程复杂、周期长，在客车订单生产的设计中首要考虑效率问题，故悬置系统的设计首要选取悬置元件的安装位置和角度，对于对称布置的悬置元件，左右悬置同步变化。定义设计变量(1)(2)(3)分别为前悬置在X、Y、Z 3个方向的平移；设计变量(4)(5)(6)分别为后悬置在X、Y、Z 3个方向的平移；设计变量(7)(8)分别为前、后悬置元件主轴与坐标轴Y的夹角，共8个设计变量。其中，左右悬置在X方向和Z方向的移动在坐标轴0点同侧，方向相同；在Y方向的移动分别位于坐标轴0点两侧，左右悬置方向相对，数值上表现为符号相反。各悬置的位置随设计变量的变化如表5所示。

表5中，FL、FR、RL、RR为不同位置悬置，分别表示左前悬置、右前悬置、左后悬置和右后悬置；x0、y0、z0为左前悬置3个方向坐标初始位置，x0、y0、z0、x0、y0、z0、x0、y0、z0定义类似，为对应悬置的初始坐标；、分别为前悬置和后悬置主轴和坐标轴Y方向的初始角度。

表5 定义设计变量的悬置坐标和角度

2.2 目标函数

悬置系统设计要求达到较好的频率配置和解耦率，频率配置可以通过约束条件来实现。选择各阶振动主振型的解耦率达到最大值为目标函数，转换成求最小值为：

式中：ω为加权值，R为阶主振动方向的解耦率。

2.3 约束条件

3 悬置系统优化设计案例及对比研究

3.1 设计案例及对比研究

根据前面建立的优化设计模型，采用遗传算法对建模过程中不考虑驱动皮带和考虑驱动皮带两种情况进行优化设计，两种模型优化过程采用完全相同的设计变量、目标函数和约束条件。优化后各设计变量的值与原系统对比如表6所示。

由表6可见，在优化后与原系统相比，前悬置在X方向前移，Y方向远离动力总成本体向外移，Z方向上移；后悬置在X方向下移，Y方向不考虑驱动带时内移，考虑驱动带时外移，Z方向下移，除后悬置Y方向外移动方向总体一致。受到驱动带刚度和位置的影响，两种建模方式的优化结果在数值上有较大差异，主要表现在后悬置上，相比于不考虑驱动带时X方向后移增加208 mm，Y方向外移62 mm，Z方向进一步下移113 mm。在角度方面，优化后前后悬置与Y的夹角与不考虑驱动带建模相比，前悬置减小了13°，后悬置减小了28°。

表6 悬置元件优化前后位置

为检查各自的优化效果，将优化后的设计参数进行计算，得到两种模型优化后的结果，见表7和表8。

表7 优化后系统的频率和能量分布(不考虑驱动皮带建模)

由表7可见，不考虑驱动皮带模型优化后，系统各阶固有频率在4.5 Hz到16 Hz之间，且相邻模态频率间隔在0.5以上，频率分布合理；各阶模态的解耦率都大于95%，解耦率非常高，优化效果明显。

表8 优化后系统的频率和能量分布（考虑驱动皮带建模）

由表8可见，考虑驱动皮带模型优化后，系统各阶频率分布合理，各阶模态解耦率在85%以上，相比原系统也有明显提升。对比表7和表8，两种建模方法优化后的效果，在频率上，各阶次主振动方向和频率数值都有所区别，但都满足要求；在解耦率方面，不考虑驱动带的模型得到的优化效果更加明显；考虑驱动带的模型，解耦率有明显提升，受驱动带的影响，解耦效果会差些。

3.2 设计效果振动响应对比分析

频率配置和解耦率作为悬置系统隔振性能好坏的重要指标，以此为目标函数在两种不同悬置系统模型上进行优化设计后，在各自的模型中得到了较好的效果，但得到设计参数差异显著。为了进一步对比研究两种模型在优化后与优化前系统的隔振效果，在含驱动带的动力总成悬置系统模型中施加发动机激振力，考察各悬置元件向车身传递动态响应力的情况[12]。

考虑激励时，系统振动微分方程可以表示为：

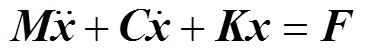
式中：为系统阻尼矩阵，发动机的激振力。

发动机的激振力可以表示为：

其中，F、F、F分别为发动机沿X、Y和Z 3个方向的水平振动激励；M、M和M分别为发动机在X、Y和Z 3个方向扭转振动激励[13]。力的作用点为动力总成质心。

使用Newmark-法求解微分方程[14]，求得动力总成质心振动响应位移()，第个悬置点的传递力响应为：

式中：k为单个悬置刚度矩阵，T为悬置角度相关矩阵，B为悬置位置相关矩阵。其中，

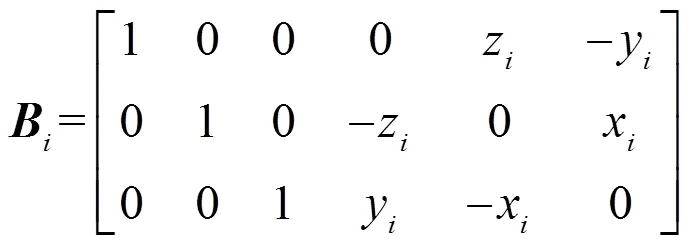
其中，k、k、k分别为第个悬置元件、、三个弹性主轴方向的刚度；α、β、γ分别为第个悬置元件坐标分别与质心坐标轴X、Y、Z的夹角，α、β、γ、α、β、γ的定义类似。

传递力响应是一个随时间变化的函数，用力的均方根值(RMS)来衡量传递力的大小，可以表示为：

式中：0,t为计算开始和截止时间，=n-0。

分别计算发动机不同转速下各悬置元件在X，Y，Z 3个方向传递力的均方根值RMS，综合考虑整个系统传递力，把各悬置同方向传递力相加，得到原系统和两种不同建模方式优化后各方向的传递力均方根值。传递力随发动机转速的变化如图6所示。

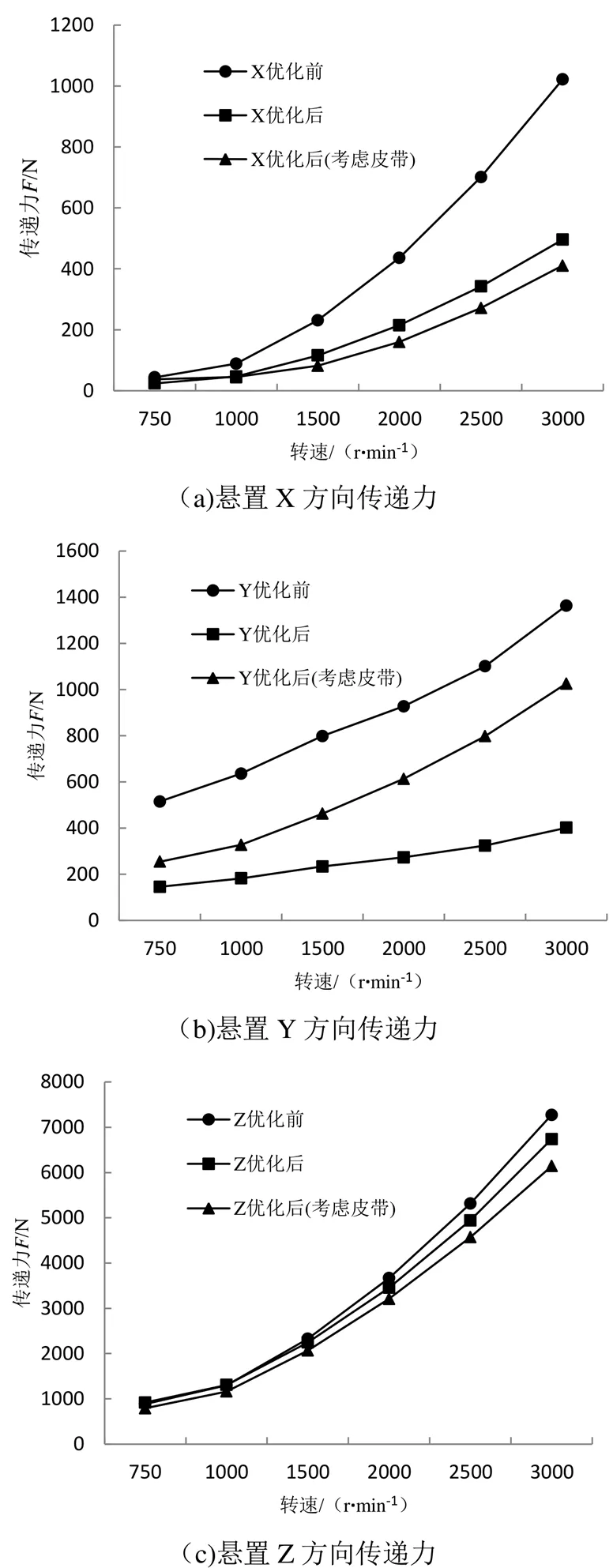
由图6的(a)，(b)和(c)可见，在两种建模方法的优化后，3个方向传递力都要比原系统好，在X方向，Z方向，不考虑驱动皮带建模优化后传递力要小于原系统，但要比考虑驱动皮带建模优化的传递力大；Y方向考虑驱动皮带的建模优化后传递力要比不考虑驱动皮带建模的优化逊色些。为进一步判断优化前后整个系统综合传递力情况，将3个方向传递力进行矢量求和，得到X、Y、Z 3个方向传递力合力随发动机转速变化情况，如图7的（d）所示。综合3个方向传递力的矢量和后，考虑驱动带建模优化后的传递力是最小的。因此，在客车动力总成悬置系统设计时，将驱动皮带建立到模型当中，会有更好的隔振效果。

4 结论

根据客车发动机前端驱动附件的实际情况，将驱动带考虑到动力总成悬置系统建模中，与不考虑驱动带模型相比悬置系统的固有频率和解耦率有明显差异；进一步以驱动带刚度为设计变量的设计研究表明系统固有频率和解耦率随驱动带刚度的变化明显。建立悬置系统优化模型，在相同条件下采用遗传算法对两种建模方式悬置系统进行优化设计，优化后解耦率有明显提升，频率配置合理；优化结果表明两种不同建模方式优化后悬置的位置变化趋势总体是一致的，但在数值上有较大差别，由于驱动带刚度的影响，本文研究的案例中前后悬置角度和后悬置位置差异较大。对两种不同建模方式优化后的结果进行动态响应比较分析，表明考虑驱动带建模对动力总成悬置系统的优化设计有更好的隔振效果，客车动力总成悬置系统在开发过程应该建立包含驱动带的悬置系统模型。

[1] 卢炽华, 刘永臣, 刘志恩, 等. 基于遗传算法的动力总成悬置模态解耦及隔振性能优化[J]. 振动与冲击, 2018, 322(14): 253-258.

[2] QIN W, SHANGGUAN W B, LUO G, et al. A method for estimating mount isolations of powertrain mounting systems[J]. Journal of Sound and Vibration, 2018, 426: 278-295.

[3] SHANGGUAN W B, LIU X A, LV Z P, et al. Design method of automotive powertrain mounting system based on vibration and noise limitations of vehicle level[J]. Mechanical Systems & Signal Processing, 2016, 76-77: 677-695.

[4] 李文凯, 曾发林. 大客车动力总成悬置系统优化研究[J]. 机械设计与制造, 2018(S2): 70-73.

[5] HAFIDI A E, MARTIN B, LOREDO A, et al. Vibration reduction on city buses: Determination of optimal position of engine mounts[J]. Mechanical Systems and Signal Processing, 2010, 24(7): 2198-2209.

[6] 王亚楠, 吕振华. 几种特殊弹性参数对动力总成-悬置系统固有振动特性的影响[J]. 清华大学学报: 自然科学版, 2012(1): 102-107.

[7] 王亚楠, 吕振华. 商用车多刚体动力装置-悬置系统振动模态特性与系统匹配分析[J]. 中国机械工程, 2011, 22(18): 2253-2258.

[8] 刘达斌, 蒋胜强, 毛江, 等. 动力总成悬置系统优化中悬置刚度灵敏度分析[J]. 中国机械工程, 2014, 25(22): 3109-3113.

[9] 曾祥坤, 上官文斌, 张少飞. 具有单向离合解耦器的发动机前端附件驱动系统的旋转振动建模及参数优化设计[J]. 内燃机学报, 2012(2): 179-185.

[10] 吴杰, 刘玉波. 动力总成悬置系统固有频率和解耦率的区间分析方法[J]. 噪声与振动控制, 2012, 32(3):12-15.

[11] 吴飞, 胡朝辉, 成艾国, 等. 综合考虑解耦率和隔振率的发动机悬置系统多目标优化[J]. 汽车工程, 2013, 35(1):18-22.

[12] 周冠南, 蒋伟康, 吴海军. 基于总传递力最小的发动机悬置系统优化设计[J]. 振动与冲击, 2008(8): 56-58.

[13] 时培成, 陈无畏, 陈黎卿. 基于联合仿真的汽车动力总成悬置系统隔振特性研究[J]. 农业机械学报, 2010, 41(2): 29-34.

[14] 郭泽英, 李青宁. 基于Newmark法的一种新精细直接积分法[J]. 陕西理工学院学报: 自然科学版, 2007, 23(2): 65-68.

Vibration Analysis and Design of Coach Mounting System of Considering Driving Belt

LI Zhi-qiang1, ZHANG Pan-deng2

（1. Department of Auto Application, Fujian Chuangzhen Communications College, Fuzhou 350007, China; 2.School of Mechanical Engineering, Tongji University, Shanghai 200092, China）

In order to study the effect of front-end driving belt on vibration characteristics and vibration isolation design of powertrain mounting system, the mounting system model of considering drive belt was established. The influence of the driving belt on the vibration characteristics of the mounting system was analyzed. The optimal design model was established based on the mounting position and angle as the design variables, and the genetic algorithm was used to optimize the design of the regardless driving belt and considering drive belt. The optimization results were compared and analyzed. In addition, by applying the engine excitation to the powertrain, the vibration response of the two modeling methods before and after optimization was compared. It shows that after the optimization of the considering drive belt, the transmission force response of the mounts to the vehicle body is minimized, and the design effect is better than that regardless driving belt．

vibration; coach; powertrain mounting system; modeling; driving belt; design

U461.4

A

1674-3261(2020)04-0219-06

10.15916/j.issn1674-3261.2020.04.003

2019-11-27

福建省教育厅科研资助项目（JAT170943）

李智强(1988-)，男，福建三明人，工程师，硕士。

责任编校：刘亚兵