振动谱图像识别的气门故障诊断研究*

胡甫才 薛厚强 高 硕 魏志威

(武汉理工大学能源与动力工程学院1) 武汉 430063) (高性能船舶技术教育部重点实验室2) 武汉 430063)

0 引 言

空压机作为重要的通用机械，广泛应用于船舶、家用电器、石油化工等各生产领域.气门为空压机的核心部件，恶劣的工作环境使其极易发生故障，因此开展空压机气门故障监测诊断技术的研究对于满足工程的急迫需求具有重要的意义和价值.

冲击力受气门影响，气门失效时其作用时间、强度发生改变，缸盖表面振动信号的特性随之变化.因而利用缸盖表面振动信号进行气门故障识别具有可行性[1].往复式空压机因其结构复杂、且激励源多，造成其振动信号存在较强的非平稳性，其统计量亦是时变函数，常规的时域、频域法难以有效提取出故障特征信息.Wigner-Ville分布是Cohen类时频分布中的一种典型的分析方法，频聚集性好，但对信号进行时频分析时会产生严重的交叉项，难以揭示信号的本质特征.若把Wigner-Ville分布的时频矩阵视为图像，进而利用Hough变换将待分析信号变为求解局部极大值，可以有效抑制Wigner-Ville分布带来的噪声与交叉项[2].基于振动信号的气门故障诊断的第二步是故障判据的准确提取.由于操作人员观察和分析振动谱时频图像时的主观性，现有的各种时频分析方法有时很难准确识别出潜在的、早期的微弱故障特征.为避免这种主观性，获得准确唯一的诊断结果，可采用图像特征提取和模式识别方法[3].KNN算法[4]作为一种统计学习方法，用其进行故障样本分类，易于实现，在空压机气门故障诊断中具有重要的研究意义.

为此，本文针对机械振动谱图像，采用图像识别技术，提出了一种以Wigner-Hough振动谱图像一阶时间矩、频率矩为特征参数的KNN识别空压机气门故障诊断方法.此方法以振动谱时频图像为二维输入信号，进一步分析和挖掘，通过提取二维振动谱图像的特征参数，自动识别出空压机气门故障特征，并进行了试验验证.

1 基于Wigner-Hough振动谱图特征提取理论

较多的激励源使采集到的空压缸机盖表面振动信号表现为非平稳性，其统计量亦是时变函数.基本的时域或频域分析难以掌握信号内在的本质，还希望得到信号频谱随时间的变化情况.本文利用Wigner-Hough算法[5]对其进行时频分析，揭示信号的时频特征.

设连续时间信号x(t)，t∈R，则信号的Wigner-Vill分布定义为

(1)

Hough变换的直线极坐标参数方程为

ρ=tcosθ+fsinθ(ρ≥0,0≤θ≤π)

(2)

式中：ρ为直线与平面空间中原点的距离，即极半径；θ为ρ与t轴之间的夹角.

将Wigner-Vill分布的时频矩阵看作图像，并作为变换对像进行Hough变换得到Wigner-Hough变换，即W-H变换.设信号

x(t)=ej2π(v0t+β/2t2+n(t)

(3)

式中：n(t)为白噪声.

其W-H变换为

(4)

式中：(v0，β)为参数空间中峰值点的坐标.

Wigner-Hough变换将信号检测转变为寻找局部极大值的问题，很好地抑制噪声与交叉项.

Wigner-Hough时频谱图的特征提取在根本上是一个图像识别问题.谱图特征提取方法主要有比对法、时频谱图分块,以及提取谱图本身的图形特征作为特征参数.然而Wigner-Hough谱图分辨率高，对诊断结果的影响很大.为此，对时频矩阵进行256级的灰度量化，处理方法为[6-7]

(5)

式中：G(i，j)为量化后像素点灰度值；H(i，j)为时频矩阵中点(i，j)的幅值；max为取最大值；round为就近取整.

对于时频表示，矩和边缘特性提供了重要的信息.时频能量分布Cx(t，f)的一阶时间、频率矩描述了信号在时间和频率上的平均位置和散布情况，分别为定义为[8]：

一阶时间矩

(6)

一阶频率矩

(7)

2 空压机气门故障特征分析

本文以某往复式空压机气门为研究对象.人为地将气门内侧沿径向打磨凹槽，外侧则切割两个凹口，以此进行气门早期的漏气故障模拟试验，见图1.

图1 漏气故障模拟试验

试验测试系统所使用的仪器有：丹麦某公司生产的加速度传感器，灵敏度为100 mV/g，光洋TRD-2E旋转编码器，最高响应速度为200 kHz，某公司LMS-SCADAS Ⅲ测试系统.试验时在气缸盖上布置加速度传感器，以测试出气缸盖表面振动信号.设定采样频率与单次采样时间，分别为16 kHz及2 s.首先测取正常气门的缸盖振动信号.选取的背压为0.2～1.2 MPa，控制储气罐的泄压阀以保持背压稳定，气压增量每次为0.1 MPa；然后将气门换为前述的故障气门，重复测试流程.

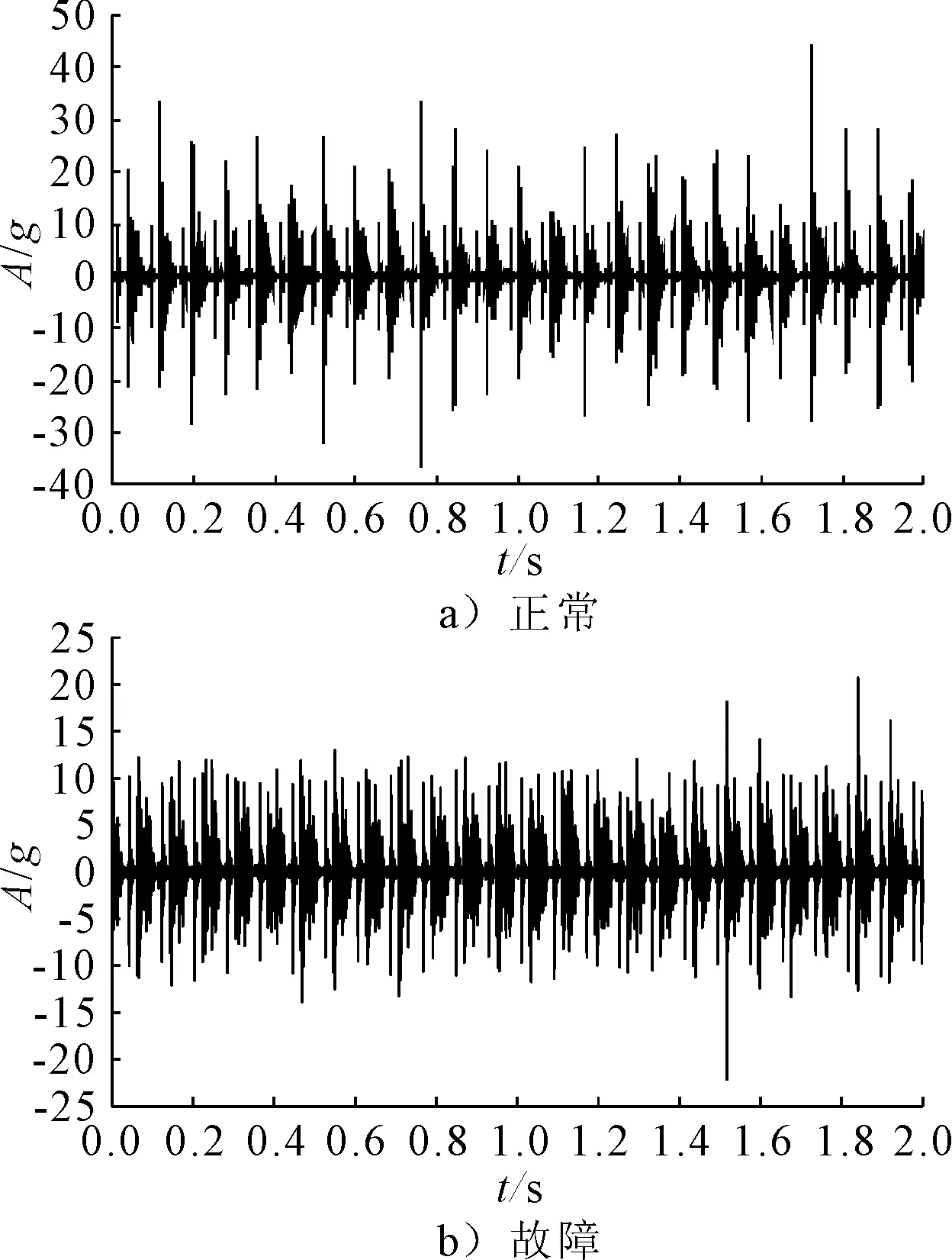
图2 0.4 MPa背压下正常和故障时域图

基于以上试验，采集到气门正常与故障状态下振动信号的时域波形见图2.鉴于篇幅关系，本文仅给示了部分分析结果.由图2可知，与故障情况相比，正常情况下的振动峰值较大.分析认为：正常情况下，气门的密封性较好，气门压力大于故障情况，从而导致振幅较大.

取0.4 MPa背压下的实测信号中任意一个周期的功率谱分析结果，频域分辨率0.5 Hz，频带0～8 000 Hz，考察气门故障是否具有频谱特征，见图3.

图3 0.4 MPa背压下正常和故障频域图

从频谱分析结果来看：正常气门情况下，振动信号的总能量较高且幅值较大，频谱无特征频率.同时，振动信号频带较宽，说明振动信号中冲击成分较高.两种气门频谱的主要区别在振动能量上，分布规律无明显差别.体现为功率谱幅值的差异，和时域分析的结果相同.

由此可见，利用功率谱不能得到信号频率随时间的变化分布.因此，采用Wigner-Hough方法对实测信号进行分析，研究故障信号的时频特征.

据此，根据Wigner-Hough算法的理论分析，采用Matlab编程得到空压机气门正常及故障状态下的Wigner-Hough变换时频谱图，部分分析结果见图4.

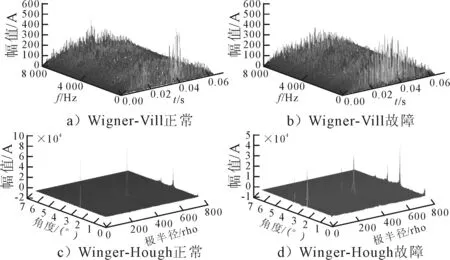
图4 0.4 MPa背压下正常和故障时频谱图

比较同一工况气门正常与故障状态下的谱图可以发现：正常状态下谱图的幅值较故障状态下谱图幅值更大一些.从理论上分析，出现此现象的原因主要是由于气门发生故障后继而发生漏气，导致了气门阀片在未达到启阀压力的情况下气体开始外泄，并引起阀片振动.此外，气体泄露使气门启阀受到的冲击变小，从而信号的振幅变小.对比时域波形和功率谱，Winger-Hough谱图正确表示了信号能量的时间-频率联合分布特点.对于Wigner-Vill分布，信号之间存在严重的交叉项，而W-H变换后峰值点被分离，有效抑制了交叉项的存在.

3 基于振动谱图像识别的气门故障诊断及试验验证

根据上述理论对气门各状态下的特征参数按时间段和频率带的分布情况进行计算，以确定故障诊断的依据.其结果见表1～2.

表1 时间分布 s

表2 频率分布 Hz

相较于正常状态，当空压机发生气门故障时，气缸盖表面振动信号在第2、3时间段内以及第3频率带内，能量分布差异较大，因此选取第2、3时间段内以及第3频率带内的能量.

根据谱图的特征参数来区分气门的工作状态是一个模式识别问题.KNN算法是统计学习方法中的一种通用学习算法，其核心思想是：特征空间中，如果某一待分类样本k个最相邻样本中的大多数属于某一类，则该待分类样本也属于此类，并具有此类别上样本的特性[9-12].

设输入样本集.

T={(x1,y1),(x2,y2),…，(xN,yN)}

(8)

式中：xi∈X⊆T为样本集的特征向量；yi∈Y={c1,c2,…,cN}为样本的类别；i=1,2,…，N；x为待检测样本的特征向量.

设输出待检测样本所属类别为y，在k个点的邻域Nk(x)中判断x的类别为

i,j=1,2,…,N

(9)

式中：I为指示函数；k为近邻个数.

选取欧式距离函数计算训练样本和待检测样本之间的距离，以刻画不同样本间的相似度.

(10)

式中：di与dj为文本的特征向量；p为特征向量维数；wik为样本di的第k维坐标.

将上述计算得到的一阶时间、频率矩作为样本数据，另外以正常与故障气门作为样本状态标签，将计算数据随机分为训练样本及预测样本.基于Matlab平台，根据上述分析采用模式识别KNN算法对其进行故障识别，当K=4时，其正确识别率可达94.75%.

为了验证文章所提方法的有效性，综合上述研究成果，基于Matlab、Labview混合编程语言开发了空压机气门监测诊断平台.整个平台集信号采集、时域分析、频域分析和时频分析于一体，其主要程序都由MATLAB实现，包括信号时域、频域、时频分析计算，特征参数提取,以及KNN故障识别.然后在LabVIEW中通过MATLAB Script来实现混合编程，实现了空压机气门的监测与诊断，其总体正确诊断率为94.38%，校验了Wigner-Hough算法在揭示空压机非平稳振动信号中的正确性、时频图像特征提取方法以及故障识别算法的有效性.这可为实现空压机气门早期故障预警提供重要的理论依据.

4 结 论

1) 往复式空压机振动信号存在较大的非平稳性，气门阀片出现磨损故障后，缸盖表面振动信号的总能量降低，表现为峰值的减小.气门振动信号的频谱能量分布较宽，体现出振动信号的强冲击性.正常信号和故障信号频谱分布相似，没有明显的特征频率和频带差别.利用基本的信号时域及频域分析手段难以准确揭示空压机气门的故障特征.

2) 基于Winger-Hough算法的振动信号时频分析，干扰项小，其时频谱图表达明确，直观准确地表征了气门正常状态下振动信号幅值较大且能量分布较为集中，气门故障状态下振动信号幅值较小且能量分布较为分散，并且有效地抑制了交叉项的存在，是一种有效的时频分析手段.

3) 一阶时间、频率矩较为稳定，可以描述图像的疏密分布和边缘特征，本文采用两个图形分布特征相结合的特征提取方式，利用KNN算法实现了故障识别，试验表明了诊断正确率为94.38%，可以认为将KNN和Wigner-Hough振动谱图像识别方法用于空压机气门故障诊断是行之有效的.