基于雷达协同的低空目标探测补盲方法

何 青，顾 兵，王晓楠

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

对于舰载雷达而言，其主要作战目标为低空/超低空飞行的反舰导弹。其飞行高度低、速度快，雷达对此类目标跟踪时，主波束照射海面。由于海面的镜像反射，雷达收到的目标回波信号是直接波信号和反射波信号的矢量和。其结果造成目标回波信号强度随着目标高度和距离而起伏变化，形成雷达盲区，导致雷达在特定距离上无法探测到目标[1]。

1 低空目标探测盲区分析

多路径效应是由于在雷达探测目标过程中，海面或地面对雷达波的反射影响目标回波信号引起的目标检测和跟踪问题。雷达在海洋环境下进行低空、掠海飞行目标探测时，受多路径影响尤为显著。多路径效应与雷达架高、目标高度、目标距离、雷达工作频率、雷达波束宽度、海面反射系数、雷达电磁波极化等因素均有关系[2]。

为研究多路径效应，建立多路径模型时通常用几何光学方法来避免复杂的电磁场换算。根据实际应用要求的不同，确定采用平面反射模型或者球面反射模型。平面反射模型相对较简单，近距离目标探测采用平面反射模型是比较准确的。球面反射模型比较复杂，计算量较大但模型精度高[3]。

2种反射模型分析如图1和图2所示。

图1 多路径平面反射模型图

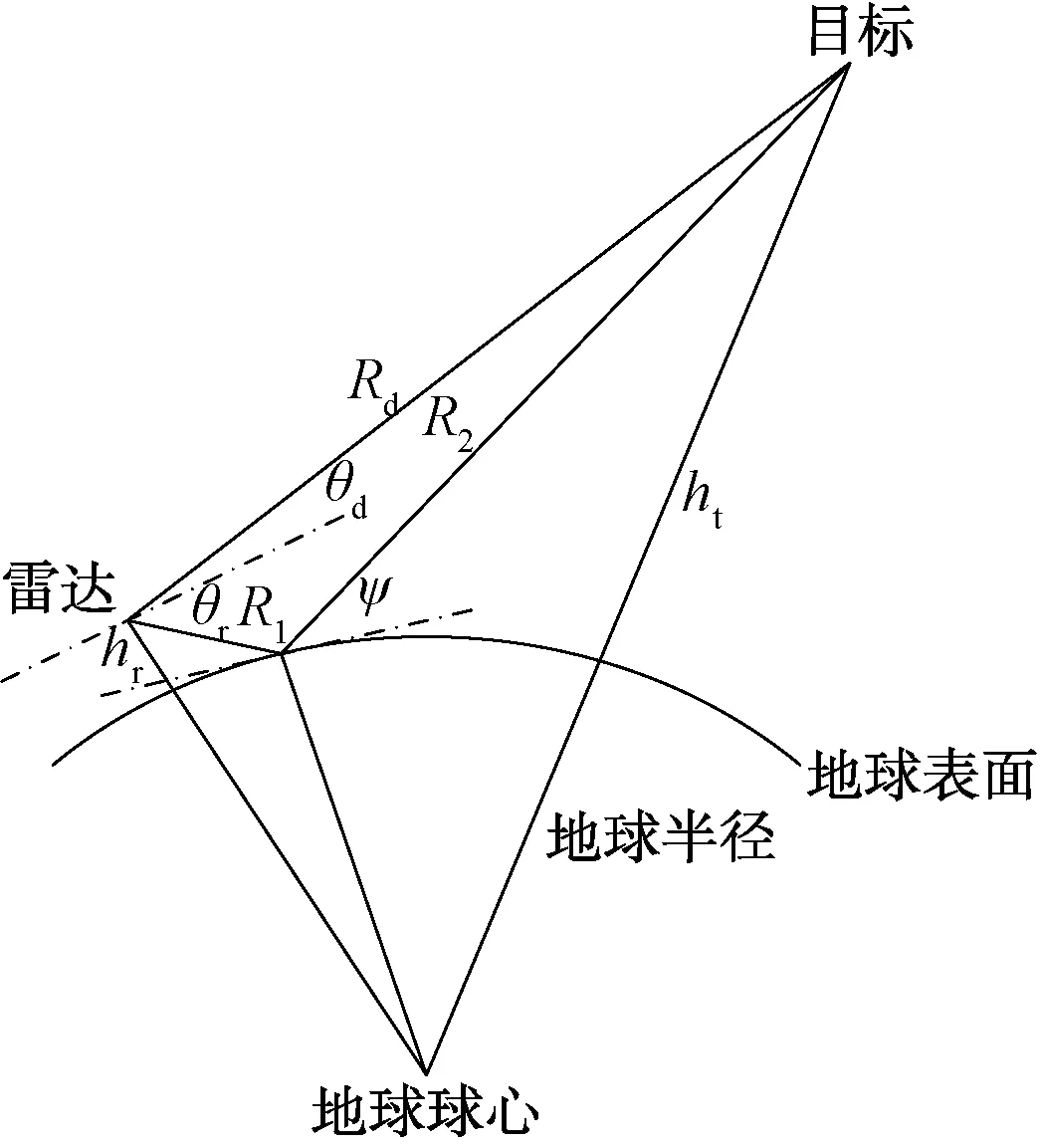
图2 多路径球面反射模型图

图中hr为天线高度，ht为目标高度，Rd为直射路径，R1和R2为反射路径，θd为直接路径的仰角，θr为反射路径仰角，ψ为入射余角。

平面反射模型中直接路径与反射路径的波程差为：

(1)

当雷达距离目标较远时，雷达的水平面与目标反射点的水平面相差角度较大，仍然采用平面反射模型会产生较大误差。球面反射中，要计算直接路径与反射路径之间的波程差，需要先用中间变量法解方程，计算反射点位置，再通过几何关系来计算得出直接路径与反射路径之间的波程差。球面反射模型中直接路径与反射路径的波程差为：

(2)

多路径条件下，对于直接信号而言，如果差信号Δd与和信号Σd同相，则多路径反射信号中的差信号Δi与和信号Σi反相，合成矢量关系如图3所示[2]。

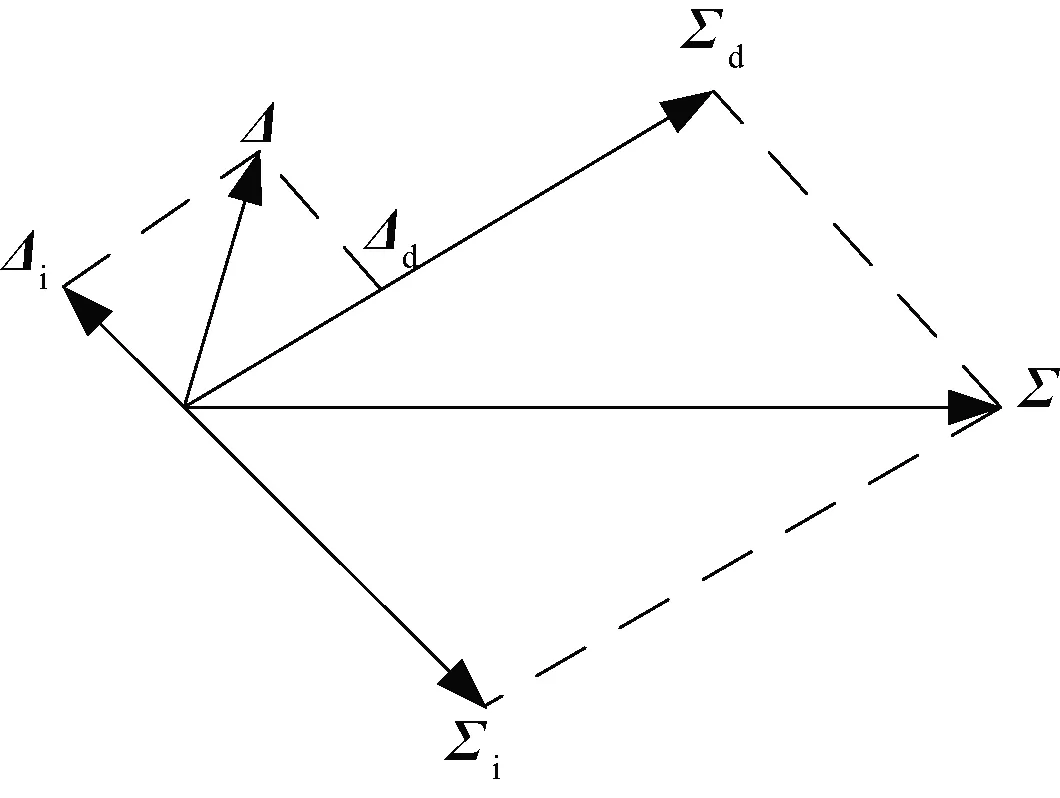
图3 多路径条件下和差信号矢量合成图

合成后的和信号为：

Σ=VΣ(θd)+ρVΣ(θr)

(3)

考虑镜面多路径效应，目标仰角θd与镜像仰角θr大小相同，则式(3)可变为：

Σ=VΣ(θd)+ρVΣ(-θd)=VΣ(θd)·(1+ρ)

(4)

式中：VΣ为和路接收电压；ρ=|ρ|ejφ，为复反射系数，φ为反射系数的相角。

复反射系数ρ与雷达极化方式、工作频率、擦地角ψ和表面介电常数等因素有关，在理想镜面反射条件下，当擦地角ψ很小时，信号的总相移接近180°，ρ=-1，直接信号与反射信号相互对消，和路信号为零，即和通道无输出，雷达无法检测到目标。

若目标的雷达截面(RCS)对直接路径和反射路径均相同，多路径下的雷达方程可表示为：

Rmax=Rmax0[1+ρ2g2+2|ρ|g.

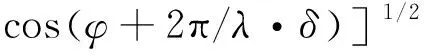
(5)

式中:Rmax为多路径下的雷达最大作用距离;Rmax0为雷达在自由空间的最大作用距离;g为目标天线增益和镜像天线增益的比;δ为直接路径与反射路径的波程差(见公式(1)、(2))。

由公式(5)可以看出，多路径下的雷达最大作用距离随着波程差δ呈现周期性的变化，导致雷达在多路径条件下存在探测盲区。

2 雷达协同低空目标探测补盲方法

雷达低空探测盲区由多路径效应引起，盲区的周期与雷达频率、雷达架高、目标高度和目标距离等因素相关。传统雷达通常采用频率分集或者频率捷变的方法来补盲，其原理为采用不同频率的雷达信号进行低空目标探测时，直接路径与反射路径合成的回波相位差不同，从而导致回波信号盲区位置发生变化，综合各频率回波信号，达到回波信号去相关效果，实现低空目标探测补盲的目的[4]。

利用平面多路径模型中直接路径与反射路径的波程差，可以得出其相位差Δφ为:

(6)

随着目标距离Rd的变化，相位差Δφ发生周期性的变化，并且变化的周期是不固定的。频率分集或者频率捷变利用改变雷达工作频率f的方法改变直接路径与反射路径的相位差Δφ，要达到回波去相关效果，需要雷达具备相当大的工作带宽，通常要求在9 GHz左右。在实际应用中，超宽带雷达受器件的水平、零漂、成本等诸多因素限制，频率分集雷达则大大提高了系统复杂程度和成本。

通过公式(6)可知，直接路径与反射路径的相位差Δφ还与天线高度hr、目标高度ht、目标距离Rd相关。目标高度为不可控因素，通过雷达协同方法可以实现天线高度、目标距离的变化，即将不同位置的2部或多部雷达进行协同处理、控制，实现直接回波与反射回波去相关，进行雷达协同低空目标探测补盲。

2.1 不同天线高度的雷达协同低空目标探测补盲方法

2部高度不同的雷达同时执行低空目标探测任务，利用雷达天线高度不同产生的目标多路径相位差进行雷达协同，实现探测补盲。根据去相关理论，将公式(6)变换得出雷达所需架高差为：

(7)

设定目标高度20 m，2部雷达的工作频率为10 GHz，目标距离为6 km，通过上式可计算出2部雷达所需的架高差为4.5 m。在实际工程应用中较容易实现，特别适用于同平台雷达协同目标探测任务。

2.2 不同目标距离的雷达协同低空目标探测补盲方法

2部与目标距离不同的雷达，同时进行低空目标探测任务，利用雷达与目标距离的不同产生的目标多路径相位差进行雷达协同，实现探测补盲。根据去相关理论，将公式(6)变换得出雷达所需架设距离差为：

(8)

设定目标高度20 m，2部雷达的架高为15 m，2部雷达工作频率为10 GHz，通过上式可计算出2部雷达所需的架设距离差为20 km，实际工程应用中较难实现。

综上分析，通过架设高度不同的2部雷达，进行协同低空目标探测任务，理论上可以比较容易实现目标的探测补盲。

3 仿真分析

仿真设定参数如下：目标RCS为0.1 m2，高度20 m，A雷达工作频率10 GHz，架高为15 m，发射功率1 kW，天线增益36 dB，噪声系数6 dB，改善因子33 dB；B雷达工作频率10 GHz，架高为19 m，发射功率1 kW，天线增益36 dB，噪声系数6 dB，改善因子33 dB。

在不考虑多路径盲区影响的情况下，雷达威力仿真如图4所示，雷达最大作用距离为13.7 km。

图4 雷达威力仿真结果(无多径影响)

设定3级海情，A雷达威力仿真结果如图5所示。雷达在10 km内的约4.8 km、6.2 km、8.7 km 3处出现探测盲区，此时接收回波信噪比小于雷达最小可检测信噪比，雷达无法发现目标。

图5 A雷达威力仿真结果

设定3级海情，B雷达威力仿真结果如图6所示。雷达在10 km内的约4.6 km、5.7 km、7.3 km 3处出现探测盲区，此时接收回波信噪比小于雷达最小可检测信噪比，雷达无法发现目标。

图6 B雷达威力仿真结果

A雷达与B雷达协同后威力仿真结果如图7所示。雷达协同后在10 km内接收回波信噪比均大于雷达最小可检测信噪比，无探测盲区。仿真中雷达架高相差4 m，符合舰载平台雷达的实际情况。

通过以上仿真结果可以看出，利用不同架高的雷达协同进行低空目标探测，可以达到目标探测补盲的效果。

4 结束语

低空目标的探测盲区一直是雷达目标探测的难题，本文基于雷达架高对接收回波的影响，提出了一种基于雷达协同的低空目标探测补盲方法，并仿真分析了利用该方法进行低空目标探测补盲的有效性，证明该方法具有较好的工程应用价值。

图7 雷达协同后仰角测量误差仿真结果