基于BP算法和LSTM算法的汽车销售预测模型比较研究

李钊慧 张康林

摘 要：汽车销售过程中存在新车与二手车销售不平均、放款受季节影响等问题。而人工神经网络适用于处理不规则、非线性的汽车销量数据，基于BP算法和LSTM算法建立15日的汽车销售预测模型，比较二者的预测效果，可以帮助销售商处理放款量及放款金额的不确定性问题。结果显示，LSTM模型对于受季节因素影响的汽车销售数据在销售台数和销售金额趋势预测方面更为有效合理，在模型预测的精度上比BP模型效果更优，可为汽车行业的销售预测提供参考。

关键词：人工神经网络;销售预测;BP算法;LSTM算法

中图分类号：F724.7      文献标志码：A      文章编号：1673-291X（2020）20-0084-05

引言

随着我国人们生活水平的提高，我国汽车销售市场重心开始下沉，汽车行业痛点显现。在此竞争局面下，以经销商的销售能力为中心解决强压库存的难题，以节约汽车相关企业的经营成本和经营风险为目标显得尤为重要。通过建立汽车销售预测模型，合理规划产能安排放款金额，免掉不必要的多余费用，是降低经营成本的重要举措。

BP算法是人工神经网络中重要的一个算法，在解决非线性系统问题时优势明显，不少学者通过进行持续改进[1-3]，在预测股价、电力、钢铁等方面应用价值突出[4-6]。杨婷、杨根科、潘常春[7]（2009）利用BP神经网络定性分析每个因素的权重，建立了汽车故障率预测模型。罗戎蕾、刘绍华、苏晨[8]（2014）将对服装销售影响因子分为季节、节假日和品类因素，建立3层BP神经网络学习销售预测网络模型。王锦、赵德群[9]（2018）将BP神经网络与遗传算法相结合，发现可以更好地预测北京市某大型超市的大米日销量。而LSTM算法是循环神经网络的一种变体，在深度学习后能更好地处理序列化数据，其在电力负荷、流量等预测具有良好的预测效果[10-13]。李鹏、何帅等[14]（2018）使用自适应矩估计算法进行深度学习发现LSTM算法在预测中精度较高。李珍珍、吴群[15]（2019）在Pytorch框架下搭建LSTM模型对上证、深证指数和国内特定4支股票的最高价进行预测，发现在短时间内股票预测结果与真实值接近程度高，长时间则出现相差较大的问题。宋刚、张云峰、包芳勋和秦超[16]（2019）通过自适应学习策略的PSO优化算法对LSTM模型的关键参数进行寻优，提高股票价格预测精度。因此，本文选择使用BP神经网络和LSTM神经网络解决汽车销售相关的预测问题。

一、BP算法和LSTM算法原理

（一）BP算法简介

BP（Back Propagation）神经网络由Rumelhart和McClelland等科学家[17]（1986）提出，用梯度下降法的基本理念和梯度搜索技术，目标是求得网络的实际输出值和期望输出值的误差均方差为最小。BP神经网络由输入层、隐藏层和输出层三部分组成，结构示意如图1所示。

图1中，Xi表示来自第i个神经元的输入，Wh表示从输入层到隐藏层第i个神经元的连接权重，ho表示偏置项，f（x）表示激活函数，O表示模型计算输出值，y表示最终输出值。本文选取的是Sigmoid+Adaline模型。

在上述模型的基础上，又细分为4组。

由其特性，本文将收集到的汽车销售数据分为15天为一周期，将对象分为二手车、新车，使得BP算法在应用于解决本文中汽车销售放款问题时可以一定程度上避免陷入局部极小值。

（二）LSTM算法简介

LSTM（Long Short Term Mermory network）神经网络在1997年由Sepp Hochreiter[19]等人提出，主要改良了循环神经网络在处理距离较远的序列时的梯度消失问题。LSTM实现了3个门计算，即遗忘门、输入门和输出门。？滓表示sigmoid激活函数，wf表示遗忘门的权重矩阵，wi表示输入门的权重矩阵，w′c表示更新门的权重矩阵，wo表示输出门的权重矩阵，bf表示遗忘门的偏置，bi表示输入门的偏置，b′c表示更新门的偏置，bo表示输出门的偏置，ht表示t时刻的输出，C′t表示t时刻更新的细胞状态。

二、某公司汽车销售预测分析

（一）处理数据

1.日期整理

本文收集并整理了某公司汽车销售数据，并非传统连续型数据，时间范围为2017年9月30日至2019年2月20日，共510个离散数据，补全缺失的数据。

2.数据分类

按照汽车类别分为两类：①新车;②二手车。按照汽车销售属性分为两类：①销售台数;②销售金额。做预测时分别预测台数和金额，给公司的库存系统和业务员的业绩重点提供参考。为了避免陷入局部极小值和梯度消失等问题，将510天的数据每隔15天为一周期进行合计，缺失值以0為记录，构建完整有效的数据集，预处理后得到：①15天新车台数;②15天新车销售金额;③15天二手车台数;④15天二手车销售金额。

（二）BP算法和LSTM算法参数设计

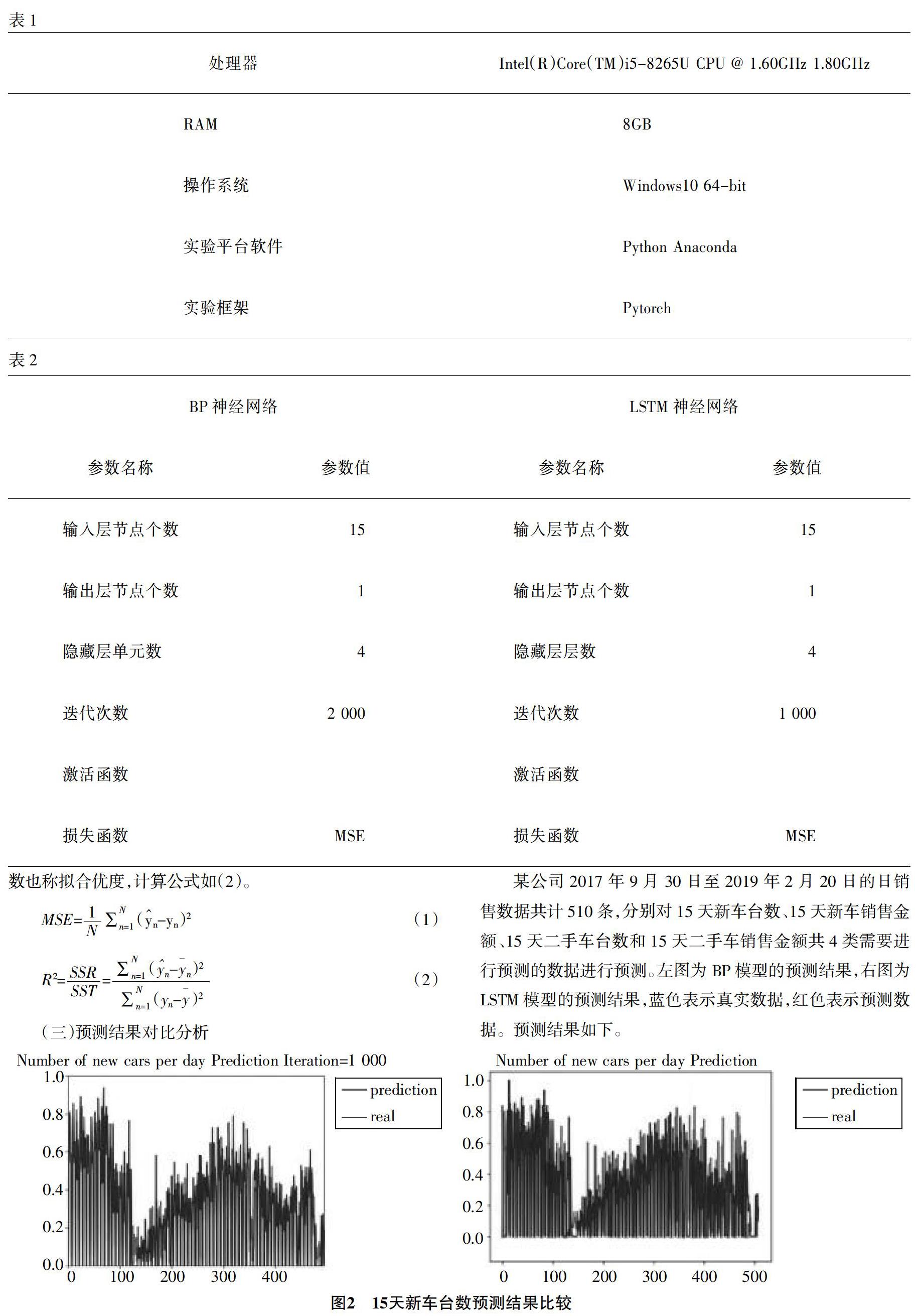
本文的硬件环境和软件环境，具体如表1所示。

根据对数据的预处理分析，BP和LSTM训练模型的参数设置总结如表2所示。

本文选取均方误差（MSE）以及决定系数（R2）作为两个模型预测精准度的评价指标[21，22]，其中，均方误差是指参数估计值与参数真值之差平方的期望值，计算公式如（1）;决定系数也称拟合优度，计算公式如（2）。

（三）预测结果对比分析

某公司2017年9月30日至2019年2月20日的日销售数据共计510条，分别对15天新车台数、15天新车销售金额、15天二手车台数和15天二手车销售金额共4类需要进行预测的数据进行预测。左图为BP模型的预测结果，右图为LSTM模型的预测结果，蓝色表示真实数据，红色表示预测数据。预测结果如下。