深时全球海平面变化重建方法的回顾与展望

许艺炜，胡修棉

南京大学 地球科学与工程学院，南京 210023

全球海平面变化是指海平面在全球规模上相对于一个固定基准面（例如地心）的高程变化（Kendall and Lerche, 1988）。在地质历史时期，全球海平面一直处于不同速率的变化中，影响着古地理、古生物、古气候以及能源矿产的分布。例如，全球海平面的变化直接影响海陆分布，从而改变区域气候和水文循环（Ramstein et al., 1997）。海平面上升和下降同时改变了海洋生物的生存环境，进而影响海洋生物多样性（Hallam, 1992a；Holland, 2012）。高海平面时期通常会伴随着大洋缺氧环境的扩张（Ramkumar, 2016），有利于烃源岩的保存，同时高水位时期也是碳酸盐储层发育的时期。据估计，处于高水位时期的白垩纪油气储量占世界油气总储量的30%以上（Klemme and Ulminshek, 1991）。

现今全球海平面正以3.6 mm/yr速度上升（IPCC, 2019）， 据估计到2100年全球海平面可能会比现今上升2 m（Bamber et al., 2019），这将引起179万平方公里的土地流失，1.87亿人口失去居住地（Nicholls et al., 2011）。如果全球气温持续上升，地球上所有冰川融化，将会引起全球海平面上升80 m（未考虑重力均衡）（Poore et al., 2000），这将对中国产生严重的影响，例如目前中国东中部地区（包括长三角地区、珠三角地区、环渤海地区）以及沿长江经济带低海拔地区（江苏、安徽、江西、湖北、湖南等）、台湾省西部沿海地区、香港和澳门的全部地区、海南省的大部分地区将被海水淹没（图1）。全球海平面变化深刻地影响着人类社会，联合国政府间气候变化专门委员会（Intergovernmental Panel on Climate Change，IPCC）出版的评估报告会根据数学模型来预测未来全球海平面变化趋势、速率和幅度以探讨海平面上升可能产生的潜在危害。但模型预测的可靠程度取决于当下学界对全球海平面变化驱动机制的认知程度。事实上，迄今为止，学界对不同气候状态下以及不同时间尺度下全球海平面变化的驱动机制尚未达成共识，而一条高精度的深时全球海平面变化曲线是解决这些问题的基础。

海平面重建方法是恢复深时全球海平面变化的关键，因此本文从海平面变化研究历史出发，回顾了主要的深时全球海平面变化重建方法，并以白垩纪海平面重建为例，展示深时全球海平面重建的困难和争议点，并展望未来深时全球海平面变化重建。

1 全球海平面变化研究历史

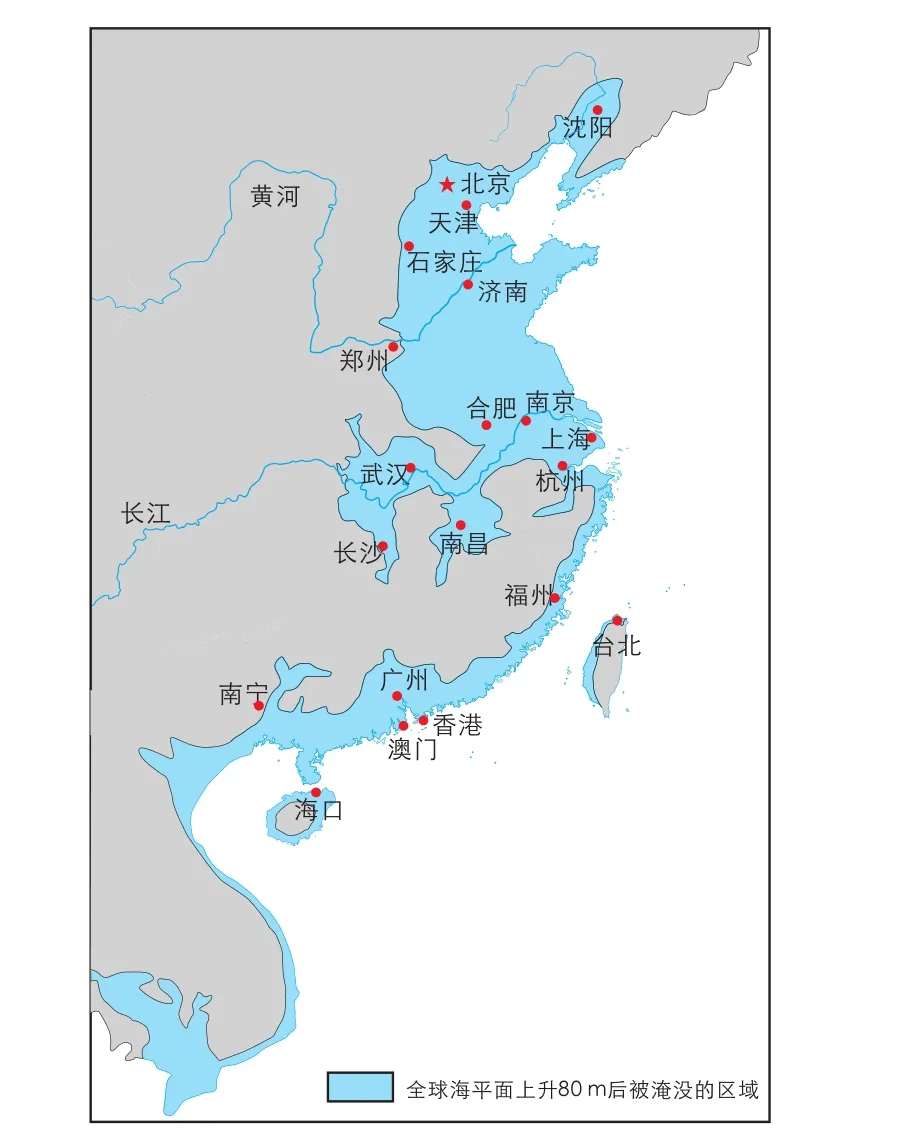
图1 全球海平面上升80 m后东亚大陆淹没区域分布示意图（修改自https://atlas-for-the-end-of-the-world.com/world_maps/world_maps_sea_level_rise.html）Fig. 1 The distribution of submersed area of East Asia with 80 meters sea-level rise (Modified from https://atlas-for-the-end-of-theworld.com/world_maps/world_maps_sea_level_rise.html)

全球海平面变化这一思想起源于古代的洪水神话和传统水成论观点（Dott, 1992a）。后者认为地球上出露的岩层是全球海平面不断下降的结果。尽管该思想萌芽于19世纪初期，但全球海平面变化这一词汇直到1888年才由Eduard Suess首次提出，他在研究欧洲第三纪的沉积物时发现在巴黎盆地、莱茵河峡谷、意大利、Pannonian盆地、Vienna盆地、加利西亚以及黑海地区的海侵过程是可以对比的，并据此推测这是全球海平面变化的结果（Hallam, 1992b）。同时，Suess认为海平面变化是不对称的，由于地球冷却收缩，导致海底发生沉降，引起海平面快速下降，而连续的沉积物充填则引起海平面缓慢上升（Hallam,1992b）。与 Suess观点相似，Chamberlin（1898）认为全球范围的不整合面是由于全球海平面下降造成的，因此可以用作地层对比，这一观点对美国学者产生了深远的影响，并成为层序地层学思想的起源之一（Dott, 1992b）。

20世纪30～40年代，全球韵律旋回的成因成为当时的学术热点。伴随着对冰川和海平面变化耦合关系的认识，当时学界认为这些韵律旋回和海平面关系密切。在这期间，Umbgrove（1939）在Stille（1924）的工作基础上，绘制了第一张显生宙全球海平面相对变化曲线。Kuenen（1939）基于陆地地形曲线和陆表海面积定量地恢复了全球海平面变化，并且提出全球海平面变化的范围在25～100 m。20世纪30年代，Grabau（1940）提出了地球脉动假说，并利用全球海平面变化的等时性进行地层对比，恢复出古生代的全球海平面变化事件。20世纪60年代，由于沉积自旋回的发现，全球韵律旋回仅受海平面控制这一观点受到挑战，改变了学界对韵律旋回仅受海平面变化控制的认识（Dott, 1992a）。

20世纪60～70年代，由于油气勘探行业内地震地层资料的普及，Vail和他在Exxon公司的同事在前人的工作基础上开发出新的技术，通过地震地层学的手段识别出全球海平面信号，并出版了显生宙以来的全球海平面变化曲线（Vail et al., 1977）。随后Haq等人 不断更新不同地质时期的全球海平面变化曲线（Haq et al., 1987；Haq et al., 1988；Haq and Al-Qahtani, 2005；Haq, 2014）。大洋钻探计划也在同时期开展，深海沉积物的研究证明了前人提出的米兰科维奇旋回与冰期—间冰期之间的关系，并将全球海平面变化与全球气候变化联系在一起（Dott, 1992a）。这两项工作极大地促进了20世纪70～90年代人们对于全球海平面变化的研究热情 (Dott, 1992a)，在该时期，不同学者利用多种方法出版了数条全球海平面曲线（Vail et al.,1977; Haq et al., 1987; Pitman, 1978; Hallam, 1984;Harrison, 1990），并引起学界对全球海平面的概念、变化过程、控制机理以及气候响应等方面的探讨（李祥辉和张洁，1999）。例如国际沉积学家协 会（International Association of Sedimentologists，IAS）和国际沉积地质学会（Society for Sedimentary Geology，SEPM）在20世纪90年代曾先后出版专辑讨论构造和海平面对沉积旋回的控制作用（Macdonald et al., 1991; Dennison and Ettensohn,1994）。同一时期，利用层序地层手段恢复的全球海平面变化曲线受到很大争议，并且学界对于是否能够恢复全球海平面变化曲线（尤其是三级海平面变化）提出质疑（Kendall et al., 1992；Miall,1994；Dewey and Pitman, 1998）。

21世纪以来，Miller等（2005）在新泽西地区重建了晚白垩世以来的全球海平面变化，Ray等（2019）在总结前人关于白垩纪海平面工作基础上，验证了白垩纪确实存在大量的短周期全球海平面变化，并恢复了海平面变化的最大幅度。学界对温室气候背景下短周期海平面变化控制因素产生极大兴趣。例如：国际地球科学计划（International Geoscience Programme Project, IGCP）609项 目 在《Palaeogeography, Palaeoclimatology, Palaeoecology》杂志组织专辑讨论温室气候下陆地水储量变化对海平面的影响。同时，也有不同学者尝试使用新的方法探索深时海平面重建（Dopieralska et al.,2016；van der Meer et al., 2017）。

2 深时全球海平面变化的重建方法

地层记录是全球海平面、构造活动以及沉积物堆积共同作用的结果。全球海平面重建本质上是从地层记录中剥离构造活动和沉积物堆积的因素。目前，深时海平面重建方法和技术大致可分为五种类型，分别是地层学、沉积学、洋盆动力学、同位素地球化学以及大数据技术。这些类型可进一步细分出10种方法和技术，不同方法通过直接或者间接的手段恢复不同时间尺度的全球海平面变化（图2）。

2.1 地层学方法

2.1.1 地层回剥法

地层回剥法通过地层资料恢复基底到海平面之间的总可容纳空间变化，而总可容纳空间变化是由全球海平面变化和基底沉降这两部分组成，因此只要扣除沉积物载荷沉降和构造沉降，剩余的总可容纳空间变化代表全球海平面变化（Kominz et al., 2008）。其中去除沉积物负载的步骤被称为R1还原，去除构造沉降步骤被称为R2还原。一般操作方法如下（Miall, 2010）：

（1）去压实：假定某区域基底之上沉积了地层a和地层b，根据地层剖面的孔隙度和深度关系，恢复地层a的去压实厚度（图3）；

（2）古水深恢复：根据a层的岩性、沉积构造以及古生物信息恢复a层沉积时的古水深（图3）；

（3） R1还原（R1 reduce）：根据重力均衡原理，计算由于沉积物重量产生的沉降量。通过去压实的a层厚度和古水深，并扣除a层的沉积负载，这就是对a层的R1还原。计算出的R1量实际上就是由于构造沉降和海平面变化以及海平面变化产生的水体负载量的总和（图3）。

图2 不同重建方法或技术恢复的全球海平面变化的时间精度（海平面级别划分依据Vail et al., 1991）Fig. 2 The temporal resolution of eustatic sea level changes reconstructed by different approaches(the division of orders of sea-level changes is based on Vail et al., 1991)

（4）R2还原（R2 reduce）: 根据沉降模拟，计算出a层沉积时的构造沉降量，根据计算出的R1值，减去构造沉降量，最后获得的值就是R2还原值，也就是代表了a层沉积时的相对海平面变化。相同的方法用于b层即可获得b层沉积时的全球海平面变化（图3）。

该方法在被动大陆边缘（Miller et al., 2005；Kominz et al., 2008）、克拉通盆地（Sahagian et al.,1996）以及海底平顶山（Röhl and Ogg, 1996）的地层中得到应用。其中古水深的估计是主要的误差来源，地层的年代精度直接决定了最终恢复的海平面变化的分辨率。

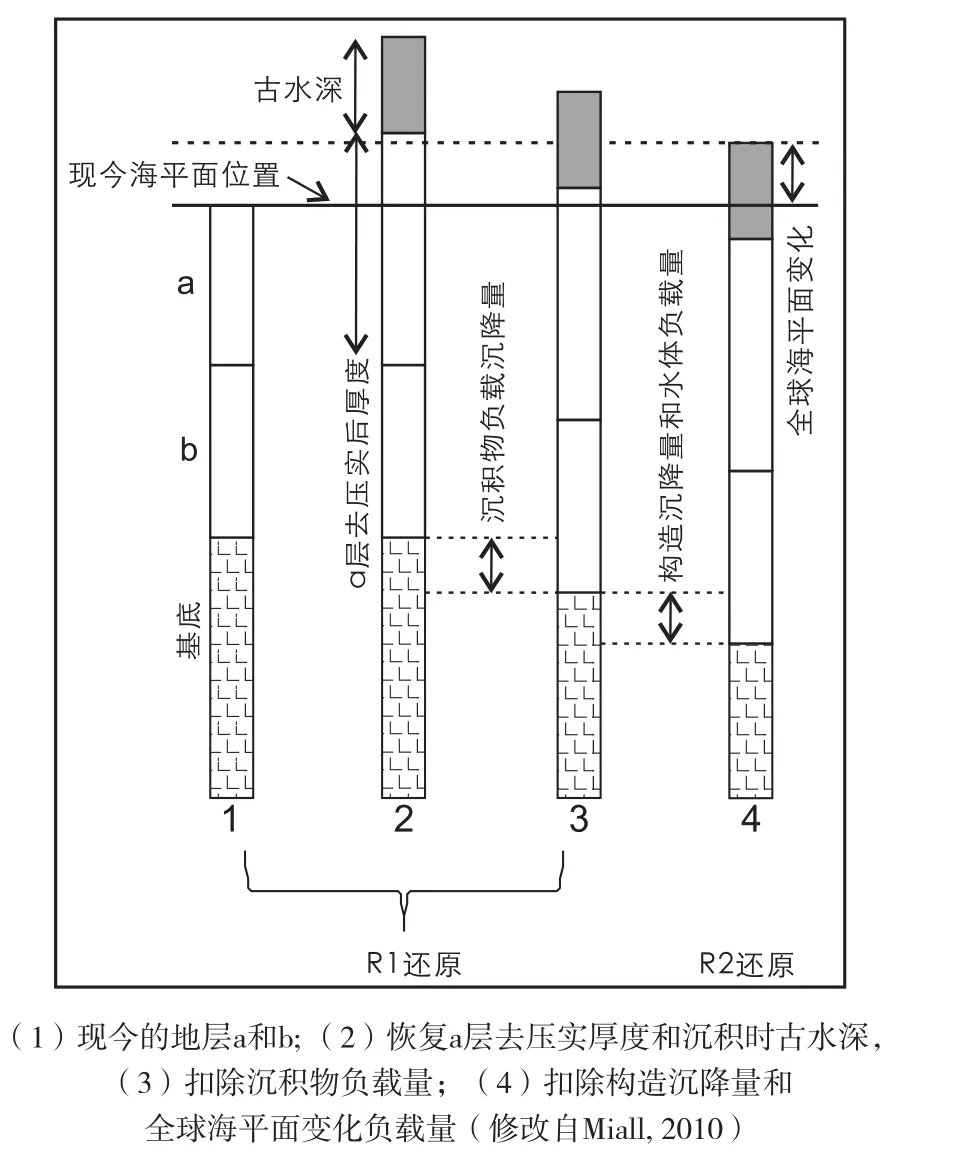
图3 地层回剥法恢复海平面变化步骤Fig. 3 The backstripping procedure to reconstruct sea level changes

地层回剥法重建全球海平面变化存在的主要问题是模拟计算得到的构造沉降量能否代表了真实的构造沉降总量。虽然该方法通常用于构造活动稳定的被动大陆边缘，但是假定被动大陆边缘沉降是一条平滑的热沉降曲线是没有依据的（Kendall and Lerche, 1988）。考虑到板内应力作用，即使是在稳定的被动大陆边缘，计算出的R2值也有可能代表的区域构造影响，而非全球海平面信号。严格意义上，通过该方法恢复的全球海平面曲线仍然是一条区域相对海平面变化曲线（王成善等，2017），需要同时代多地区的地层回剥结果进行对比才能最终确认。其次，该方法涉及到古水深估计，由于深水沉积环境估算的古水深误差过大，因此该方法更适用于能够精确估算古水深的浅海相地层。

2.1.2 层序地层学方法

层序地层学方法是通过识别层序和层序之间的关系来确定相对海平面变化。Vail等（1977）提出在地震剖面上恢复区域相对海平面变化和全球海平面变化的方法：

（1）分析海相层序，识别出不同的层序，层序边界，并确定其时代（图4a）；

（2）编制沉积层序的年代地层对比图（图4b）；

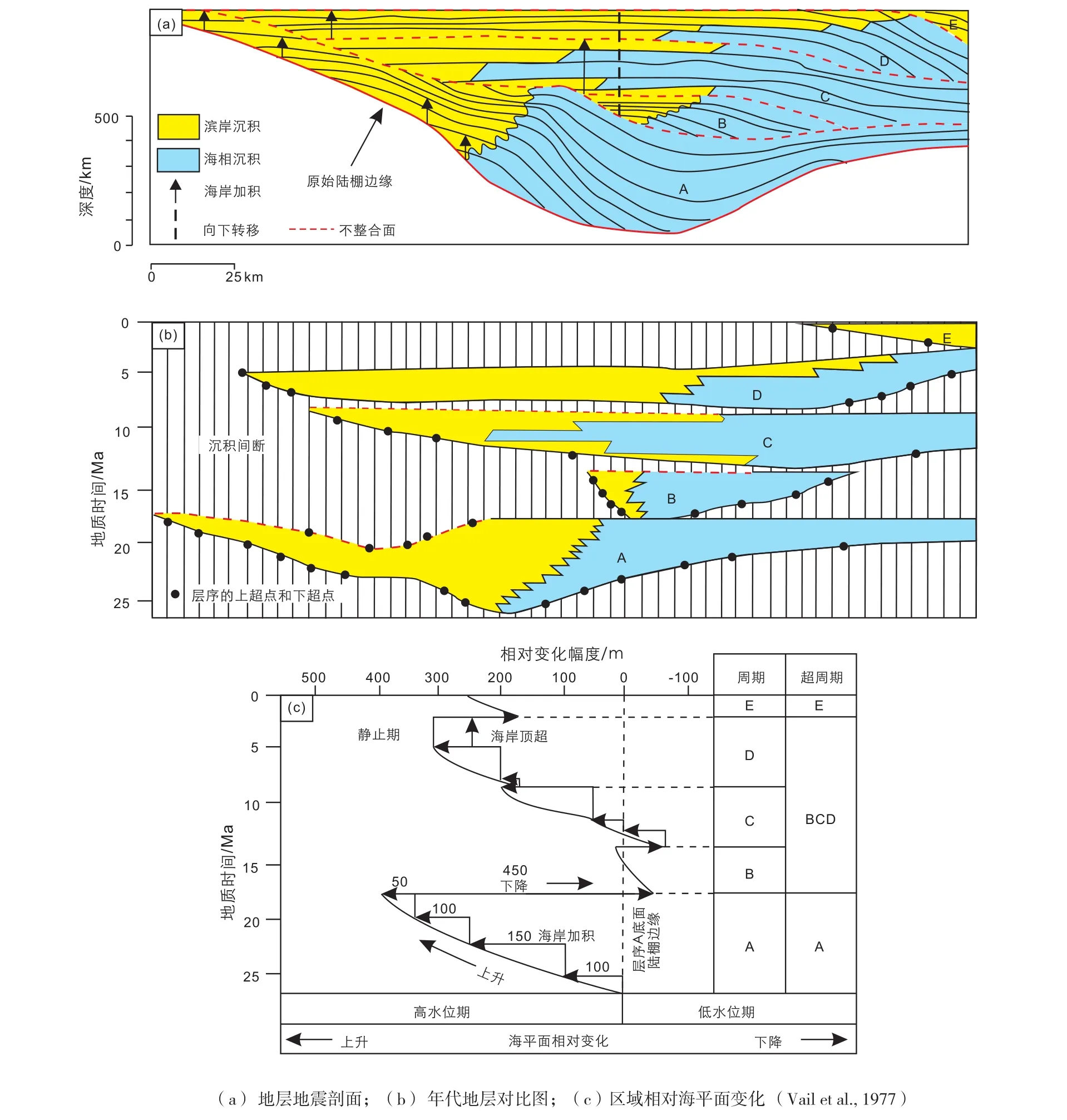
图4 利用地震资料编制区域相对海平面变化的步骤Fig. 4 Procedure for constructing regional chart of relative sea level change from seismic profile

（3）根据海岸线上超点确定海平面的相对升降幅度。例如a层序的不同上超点之间的垂直分量代表了相对海平面的上升值。而层序a中最高的海岸上超点到层序b最低的海岸上超点即为相对海平面下降幅度（图4a）。重复这些步骤，便可以得到层序B-E的相对海平面变化历史（图4c）。通过层序地层的方法获得全球不同地区的相对海平面变化过程，并把所有地区相对海平面变化幅度进行模式平均（Modal average），即可获得全球海平面变化幅度。

Vail等（1977）依靠地震资料解释绘制出了显生宙全球海平面变化曲线，其后更新的版本中加入了大量的露头层序地层的研究（Haq et al., 1987）。

早期Vail等（1977）等仅依据地震地层学的方法绘制出显生宙的全球海平面变化曲线，但是由于其使用的基础资料没有公开，确定每个层序界面是全球等时的证据没有列出，因此无法评估该曲线的可靠性。Haq等（1987）更新了全球海平面变化曲线，并列出了参考的剖面，但是并没有列出用了这些剖面的哪些数据，各种数据的权重，因此严格意义上，Haq等（1987）曲线的基础资料也是没有公开的（Hallam, 1992a；Miall,2010）。其次Vail等在进行区域层序对比时存在循环论证的问题（Miall, 2010）。例如在层序年代和生物地层及其它方法确定的年代存在矛盾的时候，Vail优先使用层序地层年代。这表明Vail先验性的假定这些层序界面是等时的，然后再进行区域对比（Miall, 2010）。此外Vail等人认为地层超覆现象是全球海平面上升的结果，但是Watts等（1982）认为单一的构造活动也可以形成超覆，例如裂谷盆地中，在裂陷期向拗陷期转化时就能形成地层超覆。在恢复全球海平面变化幅度上，Vail等人针对不同级次的全球海平面变化使用不同的方法，在恢复长周期全球海平面变化的幅度，Vail以及Haq等是依据洋盆动力学方法和大陆海泛面积方法确定的（Vail et al., 1977；Haq et al.，1987；Haq, 2014）。在短周期的全球海平面的变化幅度上，Haq声称使用了层序地层数据和氧同位素数据（Haq, 2014），但并没有给出这些数据恢复海平面变化幅度的过程。因此，利用层序地层方法恢复的全球海平面曲线，无论是海平面变化过程还是变化幅度，均受到较多的争议（Allen and Allen,2013；Miall, 2010）。

2.2 沉积学方法

2.2.1 沉积标志和沉积相方法

沉积学方法是全球海平面重建的经典方法，在不同的时间尺度均得到广泛应用。该方法恢复全球海平面变化主要依靠:

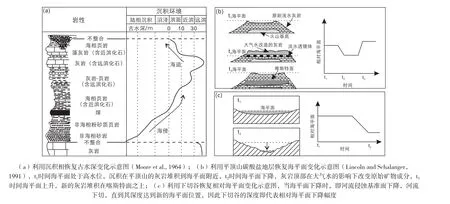
图5 利用沉积标志和沉积相方法恢复相对海平面示意图Fig. 5 Diagrams of relative sea level reconstruction by sedimentary facies and sedimentary markers

（1） 古海平面位置识别（图 5b，c）。通过平顶山的碳酸盐地层（Lincoln and Schalanger，1991）、 珊瑚阶地（Moore et al., 1982；Schellmann and Radtke, 2004）、海岸洞穴沉积物（Dumitru et al., 2019）以及下切谷（Tanabe et al., 2009）等沉积标志能够定量恢复海平面变化幅度，但是在计算时需要根据不同的模型扣除区域构造沉降量的影响（Kendall and Lerche, 1988）。例如Lincoln和Schalanger（1991）根据太平洋地区平顶山的碳酸盐地层恢复了始新世—中新世的海平面变化。

（2） 古海岸线的识别。通过识别剖面上古海岸线位置，测量不同层位古岸线的垂直距离，经过压实校正和构造旋转恢复，同样可以获得区域相对海平面变化历史。例如：Goldstein和Franseen（1995）在西班牙上中新世地层剖面上识别出的30个古海岸线位置，恢复了区域的相对海平面变化曲线。

（3） 沉积相变化 （图5a）。利用岩性、沉积构造以及古生态的信息可以恢复区域的沉积相变化，进而获得区域的古水深变化过程。由于区域的古水深变化是构造活动、全球海平面变化以及沉积物供给三者综合的结果，因此只有在构造活动保持稳定的地区恢复的沉积相变化才有可能代表全球海平面变化，而且需要和全球不同区域沉积相和恢复的古水深对比，才能确定全球海平面变化事件（Han et al., 2016；Zhang et al., 2018）和相对变化幅度。例如Hallam（2001）综合了欧洲和其它地区侏罗纪的岩相资料，通过对大陆海泛面积的改变获得长周期全球海平面变化，然后通过识别海相地层的古水深变深和变浅事件恢复短周期的全球海平面变化，获得了一条侏罗纪全球海平面变化曲线。

珊瑚阶地、海岸洞穴沉积物这些沉积指标多数用于第四纪以来的全球海平面恢复，很难广泛地用于深时海平面变化研究。而通过沉积相获得的古水深变化曲线相互对比，可以得到全球海平面变化相对幅度，但是由于区域构造和沉积物供给的影响，不可能直接恢复全球海平面变化的绝对幅度。其次这些古水深曲线对比通常是通过生物化石带进行的，但是由于地层保存以及生物区系的问题，较难实现全球范围内高精度的等时对比（Miall, 1994 , 2010）。

2.2.2 Fisher图解方法

根据沉积地层中的米级旋回厚度变化，运用投图展示相对海平面变化的方法（Fischer，1964）。具体步骤如下（Tucker, 2011）：

（1）计量一段地层内的所有米级旋回数，以及每个米级旋回的厚度。每层岩石根据岩性和埋深进行压实校正，然后利用去压实的地层总厚度除以旋回数，获得平均旋回厚度。平均旋回厚度代表了每个旋回的沉降量（图6）；

（2）进行Fisher投图，横坐标为旋回数，纵坐标为每个旋回去压实厚度与平均厚度的差异值，这样可以显示出一个层序内可容纳空间的系统变化。

该方法使用的时候有两个假设前提：（1）每个旋回的持续时间相同； （2）整个层序的沉降速率（平均旋回厚度）保持恒定。因此每个旋回的厚度与平均厚度差异代表了该旋回内的可容纳空间变化。

Fisher图解的方法适用于地层的每个旋回的顶部为潮坪相沉积，因为这样才能推测旋回的厚度代表可容纳空间。但是，每个旋回的顶部并不一定是海平面处于最高位时期形成，所以每个旋回的厚度并不能代表可容纳空间，计算出来的差值也不能代表海平面变化的绝对幅度（Boss and Rasmussen, 1994）。Boss和 Rasmussen (1994) 根据在现代巴哈马滩的研究发现旋回的厚度与可容纳空间并不具有相关性，因此旋回的厚度代表可容纳空间这一假设存在问题。其次米级旋回的成因有多种解释（例如自旋回成因），因此不能不加判别地认为这条曲线代表了全球海平面的变化。

2.2.3 大陆海泛面积方法

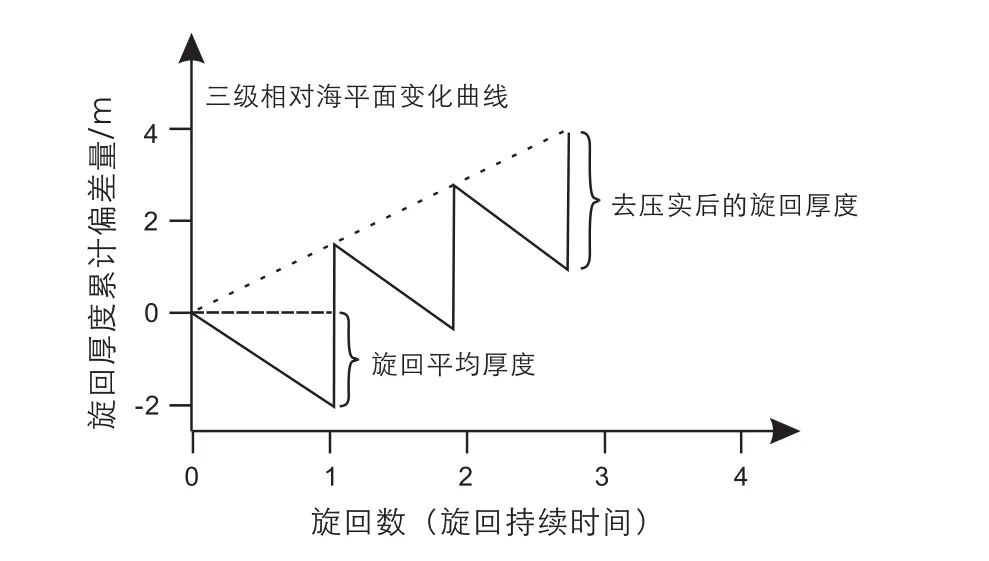
图6 利用Fisher图解编制区域相对海平面变化的步骤（Tucker, 2011）Fig. 6 Procedure for constructing regional chart of relative sea level change from Fisher plot (Tucker, 2011)

全球海平面变化将直接影响大陆被海水淹没面积的变化，因此可以根据全球陆地海泛面积的变化来近似代表全球海平面，但这只是定性表示全球海平面的相对变化。定量恢复全球海平面变化，需要知道陆地的地形测高曲线。大陆的地形测高曲线反映了地形高度和该高度占大陆总面积百分比的关系（图7b）。假定地质历史时期大陆的地形测高曲线保持一致，据此可以定量恢复全球海平面变化。其方法如下（Algeo and Seslavinsky, 1995）：

（1） 根据前人恢复的古地理图或者古滨线位置计算出全球各大陆在T时代被海水覆盖面积（图7a）；

（2）根据现今大陆的地形测高曲线，将现今大陆被海水覆盖面积x0投影到曲线上，得到一个高度值y0。将计算出的某时期大陆海水覆盖面积x1投到曲线上，获得一个高度值y1（图7b）；

（3）将获得的y1减去y0就是某一时期海平面与现今海平面的高度差。根据这个方法应用到不同的地质历史时期，就可以获得连续的全球海平面变化过程 （图7c）。

该方法对地质历史时期的大陆地形的假设前提存在问题，因为很难保证大陆地形在地质历史时期保持不变。例如白垩纪地形和当今地形存在显著差异，94 Ma时期，大陆地形比现在要平缓，而且陆地海拔普遍低于500 m（Hay et al., 2019）。Bond（1979）的研究结果表明，由于不同的大陆在不同的时期经历不同强度的构造运动，因此不同大陆恢复的海平面变化幅度不同。因此直接利用全球海泛面积计算的结果必然包含构造的信息。其次，大陆海泛面积的恢复是基于古地理图的绘制，即古地理图的时间精度决定了恢复全球海平面变化的精度。目前为止，多数古地理图的切片精度多在10 Ma左右，因此只能用于长周期全球海平面恢复。而且古地理图中的大陆海泛面积是根据保存的岩相确定的，而海侵时候的沉积地层很有可能会在海退时期被侵蚀掉，而且古老沉积地层会经历变质作用，这就导致越古老地层的海泛面积估算误差越大（Hallam, 1984）。此外，古地理图的制作过程中是将时间切片内的海相沉积全都包括进去，这必然导致获得的海泛面积大于任意时间的海泛面积。因此该方法最终只能获得一条接近长周期全球海平面变化的曲线 （Hallam,1992a）。

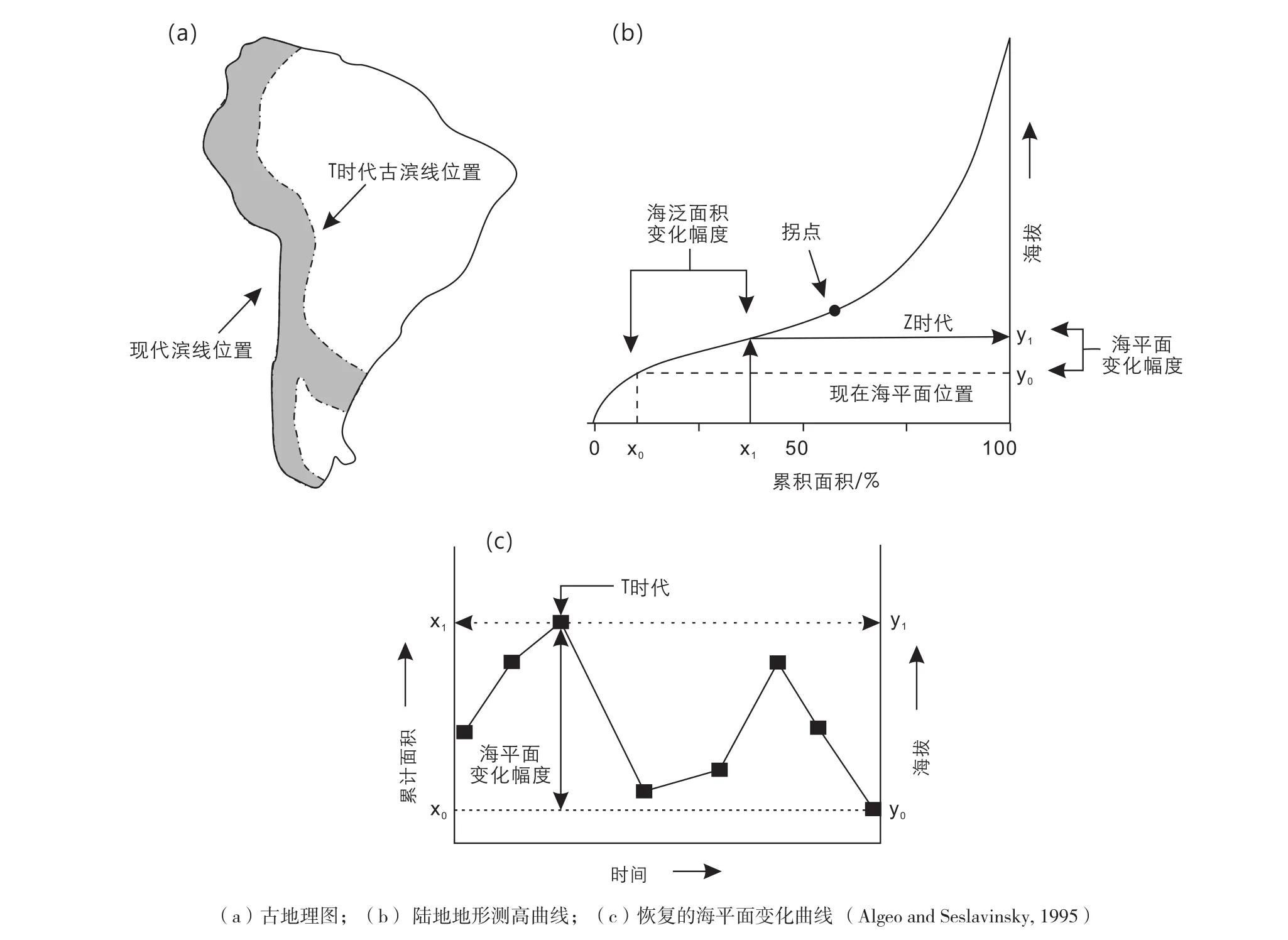
图7 利用大陆海泛面积恢复全球海平面变化步骤Fig. 7 Procedure for constructing global sea level changes from flooded continental area

2.3 洋盆动力学方法

长周期全球海平面变化主要受控于洋盆体积的 变 化（Miller et al., 2005；Conrad, 2013; Sames et al., 2016）。而洋盆扩张速率的变化决定了洋壳的平均年龄，进一步决定了洋盆的平均深度。依据洋壳保存的海底磁条带异常，以及不同地体和微陆块记录的古地磁信息可以恢复地质历史时期的大洋板块年龄分布，对于已经俯冲的洋壳年龄可以根据相对应的未俯冲板片获得 （Müller et al.,2008）。利用洋壳年龄和深度的关系函数，可以进一步计算出洋壳的深度。假定海水体积不发生变化，根据洋盆的平均深度变化以及考虑洋盆的面积变化就可以恢复全球海平面相对于当今海平面的变化值（Müller et al., 2008）。

该方法的原理决定了该方法只能恢复长周期海平面变化，无法获得三级以及更高级别的全球海平面变化。其次，该方法需要恢复地质历史时期的洋壳平均年龄，而侏罗纪之前的洋壳多数已经俯冲消失了，显然该方法很难直接用于侏罗纪之前的全球海平面恢复。第三，海水体积不变这个假设到目前为止并没有达成共识（Harrison,1999），例如Milller（2011）认为在1亿年尺度上，俯冲带走的水和火山带来的新生水是相等的。但也有学者根据地幔水和地表海水的氧同位素组成的差异，推测显生宙以来海水体积减少了6%～10%（Wallmann, 2001）。这一部分对全球海平面变化的影响应当考虑进来。

2.4 同位素地球化学方法

2.4.1 锶同位素方法

该方法和洋盆动力学方法近似。前述的洋盆动力学方法由于洋壳保存性的问题，难以应用到古生代。因此，有的学者利用海水的锶同位素变化来恢复洋壳的生产速率，进而恢复洋壳平均年龄和水深。由于洋盆体积变化，必将导致海水在陆架上的重新分布，影响大陆海泛面积，利用现今大陆地形测高曲线可以准确得到全球海平面的变化值。其基本思路（van der Meer et al., 2017）：海水的锶同位素值取决于大陆风化和地幔物质交换（洋中脊和岩浆弧风化）输送的锶同位素组成上的差异。通常大陆风化产生的锶同位素值偏高，幔源锶同位素值偏低（van der Meer et al., 2017）。幔源锶同位素通量取决于洋壳生产速率。假定陆地提供的锶同位素比值保持恒定，那么陆地的锶同位素通量取决于陆地的径流量。依据前人的模型，可以估算出大陆径流量，进而计算出陆地风化对海水的锶同位素组成贡献。扣除这一部分，即可获得幔源锶同位素通量。但该方法使用有四个假设前提：（1）海水的体积保持不变；（2）洋盆的面积保持恒定；（3）洋盆的体积不会强烈受动力地形、洋底高原、地幔柱以及沉积物这些因素而改变；（4）陆地地形测高曲线在地质历史时期不发生变化。这些假定保证了洋盆体积只受到洋壳生产速率的影响（van der Meer et al., 2017）。

该方法是通过间接恢复洋壳平均年龄来恢复全球海平面变化，因此该方法同样不能用于三级海平面以及更高级别的全球海平面恢复。而且显然洋壳动力学方法和大陆海泛面积方法的缺点都被该方法继承。因此该方法最终获得的全球海平面变化曲线误差较大，只能近似代表长周期海平面变化。

2.4.2 氧同位素方法

冰川的氧同位素组成远低于海水的氧同位素，因此当大量冰川融化时，不仅使得全球海平面上升，还会使得海水氧同位素下降。基于冰川体积和海水氧同位素之间的关系，可以用海水的氧同位素变化示踪极地冰盖体积的变化，进而估算引起的全球海平面变化。据估计现今冰川融化可使全球海水氧同位素会发生0.9‰负漂（Shackleton and Kennett,1975）。地质历史时期海水的氧同位素组成无法直接测量，可通过海相沉积记录来恢复海水的氧同位素值。但是海相沉积物的氧同位素值控制因素复杂，不仅受海水的氧同位素组成影响，还受沉积时的古温度和古盐度的影响。例如晚更新世以来深海底栖有孔虫壳体的氧同位素变化的三分之一来自于温度的变化，而另外的三分之二是由于海水氧同位素组成发生变化（Fairbanks, 1989）。

该方法被用于第四纪以来的全球海平面恢复，并且与其它指标吻合程度高（Miller et al., 2011）。但是，如前所述，沉积物记录的氧同位素会受到温度影响，这就限制氧同位素应用到深时海平面重建。其次，冰室气候下氧同位素和海平面变化之间的关系得到了很好的验证。但是温室气候下，例如两极无冰，氧同位素和海平面变化之间的关系却并不清楚，并且有可能和冰室气候期表现出相反的关系。例如Wendler和Wendler (2016) 提出温室气候下，全球海平面上升时，沉积物记录的氧同位素并不是负漂，而是表现出正漂趋势。并且即使能够确定氧同位素和海水体积之间的变化关系，也无法预测海平面变化幅度，因为无法精确模拟地壳因海水体积变化而产生的挠曲变化（Kendall and Lerche, 1988）。

2.4.3 钕同位素方法

海水中的钕同位素由放射性成因和非放射性成因两部分组成，其中放射性成因部分的143Nd由147Sr衰变而来，而非放射性成因的144Nd部分则由大陆风化为海水提供。因此，陆架中的海水中的钕同位素组成主要受控于大陆风化（Goldstein and Hemming, 2003）。当全球海平面下降时，陆地的风化程度增强，给海水提供大量的144Nd，这将导致海水的 εNd(t)下降（Dopieralska et al., 2016）。反之，全球海平面上升时，陆地风化程度减弱，给海水提供的144Nd减少，海水εNd(t)上升。由于陆架海水的钕同位素组成还会受到局部气候、区域构造活动、区域古水系、岩浆活动等影响，因此在局部区域获得的钕同位素不能直接与海平面对比，需要结合全球其它区域同时代钕同位素进行对比分析（Dopieralska et al., 2016）。

钕同位素只能用于定性地表征区域海平面变化过程，且需要多地区对比才能证明是全球海平面变化的响应。其次该方法只能用于不受深水洋流影响的浅水陆架沉积物。因为，不同洋流的钕同位素组成不同（Frank, 2002），洋流的循环模式的变化会改变区域海水的钕同位素组成，故因为洋流变化所导致的海水的钕同位素变化记录的不是海平面变化信号。并且即使是陆表海也会受到不同洋流的明显影响，因此该方法可能只适用于那些极浅或者相对封闭的陆架海域沉积物。

2.5 大数据技术

上述9种方法由于使用的假设条件、数据精度、区域构造活动等问题导致恢复出来的全球海平面变化曲线与真实的全球海平面变化存在一定的偏差，这是由于方法本身的问题所导致的。这就造成了基于不同方法、不同区域获得的全球海平面变化曲线存在差异。为了消除这种差异带来的不确定性，最好的解决办法就是综合不同区域、不同方法获得的全球海平面变化数据，识别出数据变化所显示的共同趋势，这样获得的结果能够更加真实地反映全球海平面变化信号（Rygel et al.,2008）。Rygel等（2008）和Ray等（2019）分别利用这种方法获得了晚古生代和白垩纪的全球海平面变化的最大幅度。这种方法的基本步骤如下（Ray et al., 2019）：

（1）收集全球海平面变化研究的文献，提取出海平面变化幅度的数据；

（2）根据海平面变化的时代，将所有海平面变化幅度数据投到统一的时间轴；

（3）利用统计学方法，对数据进行分析，识别出海平面幅度变化的阶段；

（4）对每个阶段的海平面幅度进行审核，根据恢复方法和构造背景进行评估，去除那些明显异常数据，获得最可靠的海平面变化幅度。

当大量海平面变化数据汇集在一起，且随着时间变化而发生系统的变化，而不是呈现出随机分布的，这表明利用大数据技术可以很好地反映全球海平面的信号。然而，目前为止，大数据技术仅用来成功恢复短周期海平面变化幅度而不是全球海平面变化过程，这是因为在确定全球海平面变化过程中需要确定海平面上升或者下降的时间，而这需要精细的时间框架。在恢复短周期的全球海平面时，需要地层对比精度达到1 Ma，但这种高分辨率的对比精度通常很难达到。

2.6 全球海平面变化方法评述

上述的10种全球海平面重建方法中，洋盆动力学方法和锶同位素、氧同位素方法的原理与全球海平面变化的成因相互联系，例如前两种方法假定洋中脊扩张速率控制着长周期全球海平面变化，因此这几种方法恢复出来的全球海平面曲线可靠性依赖于对全球海平面变化影响因素的认识。然而目前学界对于不同时间尺度下的全球海平面变化的控制因素尚存争议，所以这三种方法无法独立地恢复全球海平面变化，其最终结果的可靠性需要通过其它方法验证。

大陆海泛面积、Fisher图解方法以及钕同位素方法原理上虽然与全球海平面变化控制因素无关，但是如前所述，这三种方法使用时假设条件过多，在实际应用中无法保证满足这些条件的满足，因此这些方法很难获得一条高分辨率的全球海平面变化曲线。

层序地层学方法、沉积标志和沉积相方法以及地层回剥法在原理上与全球海平面控制因素无关，而且在实际应用中所需满足的假设条件少，可以直接的利用地层资料独立地恢复全球海平面变化。因此这三种方法最适合用于区域海平面变化重建，其中地层回剥法能够最大幅度的去除构造因素，所以利用该方法获得海平面变化幅度最为真实，是利用区域数据恢复全球海平面变化的最佳方法。而沉积标志和沉积相方法和层序地层学的方法都需要多区域数据进行等时对比，才能恢复深时全球海平面变化过程。

如前所述，单独使用任何一种方法恢复全球海平面变化都难免存在偏差和不确定性，最好的方法是通过大数据的技术，综合不同方法、不同区域的海平面变化的研究数据，可以最大限度地消除这种偏差和不确定性，获得全球海平面变化的信号。

3 全球海平面重建结果——以白垩纪为例

白垩纪作为距现今最近的一个长期处于温室气候的地质年代，该时期的全球海平面变化过程和驱动机制，一直备受关注（Hay, 2017）。而且白垩纪处于高海平面时期，在陆地上保存了大量的海相地层，同时该时期也是浮游生物大发展的时期（Skelton et al., 2002），这为白垩纪地层全球对比提供了基础。因此，白垩纪地层具有良好的深时海平面重建的条件。

3.1 白垩纪全球海平面定量恢复方法

自20世纪70年代以来，不同的学者利用不同的方法定量恢复了数条白垩纪全球海平面变化曲线（图8），现分述如下。

（1）地层回剥法

Watts 和 Steckler（1979）、Watts 和 Thorne（1984）先后利用美国大西洋被动陆缘的钻孔数据恢复了侏罗纪以来的全球海平面变化，但是由于该钻孔的年代限制的不够精确，所获得的曲线分辨率较低。Miller等（2005）根据新泽西被动大陆边缘，利用地层回剥的方法恢复了高精度晚白垩世的海平面曲线，由于使用了多种年代学方法，将地层的时间分辨率限定到1 my。Kominz等（2008）在Miller等（2005）的研究基础上增加了新的钻孔数据，并对年代进行了修正，更新了晚白垩世以来的海平面曲线。但Miller等（2005）和Kominz等（2008）分别选取不同的被动大陆边缘沉降模型，这导致长周期海平面变化上，Kominz等（2008）的海平面变化幅度要高于Miller等（2005），但是在短周期的变化上二者保持一致。 Sahagian（1996）使用俄罗斯地台的地层数据，根据地层回剥法恢复了中侏罗世晚期至晚白垩世早期的全球海平面变化曲线。由于俄罗斯地台的构造很稳定，沉积的地层厚度较薄，且地层厚度和沉积环境在侧向上保持一致，所以Sahagian（1996）认为该区域在中侏罗世晚期至晚白垩世早期没有发生构造沉降，直接排出了构造信号的影响。

（2）层序地层学方法

Vail （1977）依据地震地层识别出海岸上超点绘制了显生宙以来的一级和二级海平面变化趋势，但是关于白垩纪海平面变化所使用的资料并没有公开。Haq（1987）增加了大量的露头数据，更新了Vail等（1977）三叠纪以来的曲线，并包含了更多的三级海平面变化。随后，Haq 和Al-Quahtani（2005） 对Haq等（1988）出版全球海平面曲线的时代重新校正，并与国际地质年代（2004）时代进行对比。Haq （2014）综合了露头剖面、测井、生物地层、磁性地层等数据，与更新的国际地质年代（2012）对比，获得了更加详细的白垩纪短周期海平面曲线。但是Haq（2014）在文章中仅仅描述了每个全球性层序界面的数据来源，并没给出这些层序的生物带对比方案。

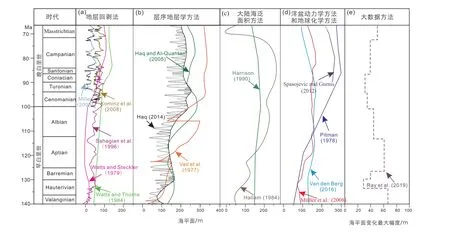
图8 不同方法恢复的白垩纪全球海平面变化曲线和海平面变化最大幅度对比（其中地质年代参考Gradstein 等，2012）Fig. 8 Comparison of the Cretaceous sea-level curves reconstructed by different methods (the geological time scale is from Gradstein et al., 2012)

（3）大陆海泛面积方法

Hallam （1984） 依据Vinogradov （1968）的全球古地理图以及北美古地理图和现今大陆地形，恢复显生宙以来海平面变化（Hallam et al., 1984）。Harrison （1990）依据Barron 等 （1981）的古地理图（时间间隔为20 Ma）为基本数据，并基于现今的地形测高数据，恢复了180 Ma以来的全球海平面变化。

（4）洋盆动力学和地球化学方法

Pitman（1978）利用全球大洋的洋中脊的长度和扩张速率恢复了白垩纪以来的全球海平面长周期波动。Müller（2008）在假设无冰气候的背景下，利用GDH-1板块模型，综合洋底扩张速率，洋底高原，沉积作用以及洋盆面积变化，恢复了更高精度的白垩纪以来全球海平面变化。Spasojevic和Gurnis （2012）的海平面恢复模型中不但考虑了洋壳生产速率、年龄的因素，还加入了动力地形的要素，恢复了90 Ma以来的全球海平面变化。van den Berg （2016）利用了显生宙的海水锶同位素信息，经过风化校正，同样获得了一条反映长周期海平面变化的曲线。

（5）大数据技术

Ray等（2019）在综合了前人发表的短周期全球海平面变化幅度文章，利用Bootstrap以及Jackknife统计学方法把白垩纪全球海平面变化幅度划分为11个阶段，并以人工审核的方法恢复了每个阶段全球海平面变化的最大幅度。结果显示，Valanginian和Aptian时期全球海平面变化幅度最大，其最大幅度变化可达60～65 m。而白垩纪中期（Albian-Coniacian）全球海平面变化最大幅度仅有30～35 m。

3.2 白垩纪长周期海平面变化

不同方法恢复的白垩纪长周期海平面趋势基本一致，均显示出全球海平面自白垩纪开始缓慢上升，一个缓慢上升然后在白垩纪中晚期达到最高水位，随后下降的趋势。但是不同曲线关于最高海平面出现的时间，幅度均存在差异。其中利用地层回剥方法恢复的白垩纪最高海平面位置最低，仅比现今高约100 m，而利用大陆海泛面积和层序地层学的方法恢复的海平面最高可达250～350 m。利用洋盆动力学恢复的白垩纪最高海平面位置介于二者之间，约为150～200 m。这些幅度上的差异主要由以下几点引起：（1）如前所述，大陆海泛面积方法使用的是古地理图的数据，而古地理图编制过程中是将该时间间隔内所有海相地层综合在一起，因此会过高的估计海相地层分布面积，进而影响到海平面幅度的估算；（2）层序地层学方法并没有恢复长周期全球海平面变化绝对幅度，Vail等（1977）显示的全球海平面幅度是依据Pitman （1978） 根据海底扩张速率变化获得的。Haq（2014）的全球海平面变化幅度是根据Harrison （1990）的大陆海泛面积的数据。因此层序地层学方法恢复的长周期海平面变化幅度可能因为早年的大陆海泛面积或者海底扩张速率数据精度不高，考虑的影响因素不完全，导致全球海平面估计与Müller等（2008）存在一定的误差；（3）Müller等（2008）认为Miller等（2005）恢复的海平面较低是因为没有考虑Farallon板块俯冲对被动陆缘产生的动力沉降的影响。

此外，不同方法获得长周期海平面变化趋势也存在差异。例如Vail （1977）重建的海平面曲线同样显示白垩纪长周期海平面一直处于上升，在Campanian达到最高值，随后缓慢下降。Miller 等（2005）和Kominz等 （2008）显示出晚白垩世海平面呈总体上升。然而Haq （2014）的曲线显示出，白垩纪海平面在Cenomanian-Turonian达到最高值。而 Watts 和 Steckler（1979）、Watts 和 Thorne（1984）的曲线显示在早Campanian达到最高值。这些不一致的现象表明，即使是长周期全球海平面变化在细节上也没有达成一致。

3.3 白垩纪短周期海平面变化

目前仅有通过地层回剥和层序地层的方法恢复出短周期三级海平面变化过程。其中地层回剥法的精度最高，获得的地层时间分辨率小1 Ma。而在Haq（2014）绘制的这条最新的曲线中，存在58个三级海平面变化，平均每个旋回持续时间约1.36 Ma。尽管这些曲线都声称代表了全球海平面变化，但是这些曲线彼此之间无法完全对比。例如Ruban （2016）对比了Kominz等 （2008）和Haq （2014）晚白垩世的全球海平面变化曲线，发现只有9个共同的三级海平面变化事件，这部分是由于Haq （2014）曲线的分辨率低于Kominz 等（2008）引起的（Ruban, 2016）。其次Haq （2014）是综合全球不同区域的层序边界获得的白垩纪海平面变化曲线，但部分三级海平面事件是假定的全球性事件，尚未被广泛的识别出来。

将Sahahian等 （1996）和Kominz 等（2008）重建的海平面对比，尽管二者都是使用地层回剥法，但是由于二者使用的区域地层数据的差异，导致二者在短周期海平面变化上差别较大，例如Cenomanian时期，Kominz等（2008）恢复的海平面旋回次数明显多于Sahahian等 （1996），而在Coniancian时期，Sahahian等（1996）恢复的海平面变化明显多于Kominz 等（2008）。这说明这两条曲线中至少有一条曲线可能仍然包含区域构造的信号。

在短周期海平面变化幅度上，Haq（2014）恢复的海平面变化幅度明显高于地层回剥法所获得的幅度。例如在Cenomanian-Coniacian时期，Haq（2014）认为短周期全球海平面变化最大幅度可以达到120 m，而Sahahian等 （1996）和Kominz 等（2008）海平面变化最大幅度很少超过40 m。类似地，Ray等（2019）基于大数据技术获得的结果认为该时期短周期全球海平面变化最大幅度应该为 30～35 m。

综上所述，无论是在长周期时间尺度还是短周期时间尺度，白垩纪尚不存在一条被广泛认可的全球海平面变化曲线。

4 讨论与展望

从白垩纪全球海平面变化的恢复来看，学界对深时全球海平面变化过程远未达成共识。这是由于不同重建方法的结果的差异导致的。因此，有学者质疑是否能够恢复深时短周期全球海平面变化的可能性（Kendall et al., 1992；Miall, 1994；Dewey and Pitman, 1998）。

如同Kendall （1992）所指出的那样，全球海平面变化重建包括两个部分。第一是确定所有的全球海平面变化事件，第二是确定每个全球海平面变化的幅度。前者的恢复依靠全球地层等时对比，而全球地层对比最常使用的方法是生物化石带对比。全球海平面曲线重建的质疑者认为由于沉积记录的不完整性、化石带的穿时性以及古生物的区系的问题，全球范围内化石带对比精度很难达到能够识别短周期全球海平面变化的要求（Miall, 1994）。这也同样是使用层序地层学方法恢复的短周期海平面曲线备受质疑的原因之一。但是近20年来，随着地质年代学的突破，放射性定年、同位素地层学、磁性地层学、旋回地层学这些定年方法的发展，以及EARTHTIME和GTS next 这些国际计划的推进，地层时代的分辨率已显著提高，并将地质年代的定年误差降低到0.1%的水平（吴怀春等，2011；万晓樵等，2014）。例如目前放射性同位素定年的精度已经可以达到1万年，旋回地层学可以建立2万年的天文标尺（吴怀春等，2011）。

全球海平面变化幅度是全球海平面重建被质疑的另一方面，因为没有可以直接测量全球海平面变化的参考点，前述的恢复短周期海平面变化的方法实质上都是相对海平面变化。然而这个观点尚未被证实。如前所述，Sahahian （1996）认为俄罗斯地台在中侏罗世晚期至晚白垩世早期没有经历过构造沉降，所以可以直接进行R1还原恢复全球海平面变化。此外，Ray等（2019）的数据很好地显示了白垩纪短周期全球海平面变化幅度的一致性。因此，随着海平面研究数据的不断增加，可以尝试使用大数据技术去获得短周期全球海平面变化幅度。

近年来，全球地层、年代、沉积、构造等数据不断涌现，同时数据的精度也在不断地提升。这是未来深时海平面变化重建的数据基础。最近，“深时数字地球”国际科学计划（Deep-time Digital Earth, DDE）拟建立高精度的年代地层框架，整合全球地质数据，恢复不同地质时期的地球演化。这为高分辨率的深时全球海平面变化重建提供了可能。在DDE的平台下，通过大数据分析、挖掘和对比，多种重建方法同时并行，有望最终获得一条精准的、资料公开的深时全球海平面变化曲线。在这个基础上，结合全球构造背景和海量地化数据等信息，探讨不同时间尺度下全球海平面变化的驱动因素，模拟海平面变化在地球气候系统中的角色，才可能使我们更清晰地认识到未来海平面变化的趋势，并为人类的可持续生存与发展提供决策依据。

致谢：感谢张世杰在文章撰写和修改过程中给予的帮助，感谢陈吉涛研究员和陈曦博士对本文提出的宝贵意见和建议。