步进电动机动态起动失步机理分析及失步解决措施

李听斌，李卓航，吴立建，朱 亮，朱加贝，章 懰，杜一东，周奇慧

(1．中国电子科技集团公司第二十一研究所，上海 200233；2．浙江大学 电气工程学院，杭州 310027)

0 引 言

步进电动机作为一种精确定位的电机，在工业中有着广泛的应用。步进电动机采用开环控制，对控制系统的硬件和软件要求较低。在开环控制中，控制系统缺少步进电动机的位置信息，易造成失步故障和越步故障。

步进电动机的建模方法和控制方法已经有了比较广泛的研究。文献[1-2]通过精细化建模，得到了较为精确的步进电动机模型。文献[3-4]研究了步进电动机的开环控制方法，开环方法无法得到步进电动机的位置信息。文献[5]中研究了通过电压电流得到步进电动机位置的方法，对步进电动机失速的检测提供了方法。

步进电动机采用开环控制，位置信号不是必要的，但是步进电动机结构和驱动方法较为特殊，存在多种原因导致步进电动机失步。文献[6]从步进电动机低频振荡的角度出发，分析了步进电动机失步的原因，并提出了解决方法。文献[7]研究了步进电动机中的谐波电磁转矩，谐波电磁转矩是造成步进电动机振荡的主要原因。文献[8]研究了混合式步进电动机在动态时电磁转矩的表达式。文献[9]通过步进电动机的运动方程，分析了步进电动机的3倍速反转的原因。现有文献中，步进电动机在转子静止的状态下起动，分析了在特定运行频率下的振荡特性和失步原因。步进电动机实际运行中会频繁起停，步进电动机暂时性停转阶段称为保持阶段，此时步进电动机某一相或几相通入恒定电流，等待下次转动指令。保持阶段前段由于惯性步进电动机处于振荡状态。若保持阶段时间较短，在下次起动时转子处于振荡状态，步进电动机存在初始速度和初始位置偏移。静态起动的失步原理分析方法将会失效，需要采用动态起动失步原理分析方法。文献[2]建立了混合式步进电动机的精细化模型，引入了衰减系数，研究步进电动机转矩的非线性特性，为步进电动机的失步分析提供了精细化模型。

本文推导了考虑初始速度和初始位置的步进电动机运动方程，将其与步进电动机的矩角特性相结合，分析了步进电动机的动态起动能力，对其失步原因做出了较为详细的解释。仿真与实验结果验证了该失步机理分析的合理性，同时，给出了针对该失步的解决方法。

1 步进电动机运动方程

两相步进电动机单A相通电，考虑到电磁转矩的非线性特性[2]，可以表示：

Te=-Kt0Ke(ia)iasin(Nrθ)

(1)

式中：Kt0为电磁转矩系数；ia为A相电流；Ke(ia)为电磁转矩衰减系数，随着电枢电流增大，电机铁心的饱和程度增加，绕组磁链减小，导致电磁转矩衰减系数衰减；Nr为转子齿数，θ为转子位置角。

步进电动机中的磁阻转矩、自定位力矩以及电磁转矩的非正弦分量会导致电机产生的转矩中存在谐波分量。谐波分量幅值相较于基波幅值较小，在步进电动机失步机理理论分析中影响不大，可以使用式(1)中的转矩作为失步机理分析的步进电动机产生的转矩。A相绕组单相通电时转子的平衡位置定义为转子位置的零位。

步进电动机机械运动方程，可以表示为如下形式：

(2)

式中:TL为电机负载转矩；J为电机转动惯量；D为电机阻尼系数；Tf为摩擦力矩。

电机中摩擦力矩较小，在分析中可以忽略。电机动态响应时，转子位置角θ通常较小。可以得到在负载为0情况下的运动方程：

(3)

单步响应即转子从平衡位置到下一个平衡位置的动态响应。假定运动方程中转子初始位置为θ0，则转子位置函数表示：

(4)

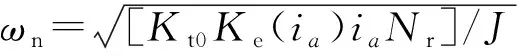
在步进电动机中，相对阻尼系数较小，步进电动机系统呈现欠阻尼状态。步进电动机的单步响应会出现振荡现象。

图1为步进电动机单A相通电的转子位置响应曲线。采用A，B两相通电，保持电流矢量的幅值相等，即A，B两相电流平方和与单相通电时电流的平方相等，转子位置响应曲线与单向通电一致，在后文中均以单A相通电分析。

图1 转子位置单步响应

步进电动机在实际应用中存在频繁起停的工作模式。步进电动机控制中，对某一相或两相通入恒定电流，使转子稳定在某个平衡状态，称为步进电动机保持状态。步进电动机在保持状态下转子位置变化与单步响应曲线相同，在一段时间内振荡。若步进电动机的下次起动时电机仍然处于振荡阶段，步进电动机初始位置会发生变化，初始速度不为零。考虑初始速度和初始位置时，式(4)可改写：

(5)

式中：ω0和θ0表示初始速度和初始位置。

可以将函数进一步写成：

θ(t)=e-ζωntA0cos(ωst-arctanx0)

(6)

式中：

(7)

(8)

由式(6)可知，转子位置函数振荡幅值和相位受初始速度和初始位置影响，但其系统频率不会受到影响。

2 步进电动机矩角特性

2.1 步进电动机绕组通电顺序

步进电动机正常运行时，定子绕组通电相的切换频率为工作频率。两相步进电动机采用八拍控制策略时，工作相通电顺序为A+→A+B+→B+→B+A-→A-→A-B-→B-→B-A+→A+，其中，A+表示A相通正向电流，A-表示A相通反向电流，B+，B-同理。每次切换工作相，步进电动机稳态转子位置角变化1/2个步距角。

2.2 步进电动机空载矩角特性

不改变步进电动机绕组通电状态，即一相或几相绕组同时通以直流电流时，电磁转矩与转子位置角的关系，称为步进电动机的矩角特性：

Te=f(θ)

(9)

步进电动机的矩角特性可以反映步进电动机转子位置和电磁转矩之间的关系。将位置函数与步进电动机的矩角特性结合，可以分析步进电动机的动态起动能力。

以电机单A相通电为例，定义步进电动机A相通入恒定电流，转子稳定时的转子位置角为0。由式(1)可知，步进电动机的矩角特性可以通过电磁转矩系数和通入A相的直流电流大小确定。

图2中，Tk表示电机的最大静转矩，即保持转矩。TL1和TL2表示负载转矩；iN表示额定电流。由式(1)可知，保持转矩Tk=Kt0Ke(ia)ia，与步进电动机转矩系数和电流有关。

图2 步进电动机矩角特性

电机负载转矩为0时，P0点为步进电动机的稳定平衡点，W01与W02之间为电机稳定区间。当电机转子位置角θ向左偏移P0点，但仍然处于稳定区间内，空间上表现为步进电动机反转。此时步进电动机电磁转矩为正，步进电动机转子位置角在电磁转矩作用下经过一段时间回到P0点，当步进电动机转子位置角θ向左偏移出稳定区间，电磁转矩为负，电机转子在电磁转矩作用下不能回到零点。

当转子位置角处于稳定区间内，步进电动机正常运行；向左偏离超过W01，步进电动机失步；向右偏离超过W02时，步进电动机越步。在之后的失步分析中，这作为判断步进电动机失步的标准。随着电机的运行，只要转子位置离开稳定区间，就可以判断步进电动机已经失步。

当步进电动机通电相改变时，步进电动机矩角特性也会随之改变。对于两相步进电动机，当通电相由A+切换到A+B+时，矩角特性曲线向右平移π/4电角度，即1/2个步距角，稳定区间也会随之向正方向移动π/4电角度。

2.3 负载转矩和电流对矩角特性的影响

若通入电流保持不变，负载转矩为TL1时，图 2中步进电动机稳定平衡点在负载转矩作用下转移到P1点，不稳定平衡点转移到W11与W12，即稳定区间在负载状态下转移到W11与W12之间。

当电机负载增大时，负载转矩由TL1变为TL2时，电机稳定区间为W21与W22之间，虽然此时的稳定区间宽度未变，但转子的反向回转不失步的理论稳定区变窄，电机就容易发生失步。负载越大，转子反向的理论稳定区间越窄，电机就越容易发生失步。

当电机通入的直流电流减小时，电机矩角特性曲线如图2中虚线所示，空载时稳定区间宽度未变，空载时电机稳定性不受影响，但是在负载情况下，电流减小会使转子的反向回转不失步的理论稳定区变窄，电机就更易发生失步。

3 失步机理分析

3.1 动态起动导致失步

图3将矩角特性曲线与位置函数曲线综合考虑，可以直观地分析动态起动的失步原因。主坐标系为矩角特性曲线，副坐标系为转子位置函数曲线，两个坐标系的横坐标均表示转子位置角。若L1表示A+相通电时的矩角特性曲线，L2、L3则分别表示A+B+相、B+相通电时的矩角特性曲线。

图3 矩角特性与位置函数曲线

步进电动机运行时，每次切换工作相，以A+相切换到A+B+相为例，图3中矩角特性曲线变化1/2步距角，由L1变为L2。转子平衡位置也会平移1/2个步距角，由P1变为P2。正常工作下每次切换工作相时，转子初速度为正值且不变，以获得稳定的转速，此时转子位置位于前后两次平衡点P1与P2之间的S1点，并且在电磁转矩的作用下，转子由S1点运行到S2点。以此类推，在下次切换工作相时，初速度不变且转子位置位于S2点。由此可知，在所有S点处转子初速度ω0和相对平衡点位置θ0相等，步进电动机切换频率较快，在正常运行时可以获得平稳的速度。在正常运行时的位置函数中x0小于0(初始速度大于0，初始位置小于0)。

在保持阶段，电机再次起动时间不确定，若电机在振荡第一次波谷，即A2点附近起动，从图3的位置函数曲线上可以看出，转子此时位置落后于正常运行时的位置S2。在一定范围内，转子位置越远离平衡点，电磁转矩越大，有利于将转子牵回正常位置。但是注意到此时转子位置落后平衡位置较远，也增加了起动难度。所以在振荡波谷附近起动会出现两种情况：一种是在比负载转矩大的电磁转矩作用下，转子能够被牵回到正常工作状态；另一种是尽管电磁转矩大于负载转矩，但因转子位置落后正常位置较远，且转子速度无法跟踪定子磁场变化，进一步加剧了转子相对于平衡点位置θ0的变大，从而造成失步现象。

在保持阶段，若电机在A1点起动，转子位置反向通过上一个平衡点，此时初始速度小于0，初始位置小于0，与正常工作时的位置函数中的x0相比，此时的x0更大且大于0。即此时位置函数的相位滞后正常工作时位置函数的相位，转子位置到达下一个S点所需要的时间更长，工作频率保持不变则容易引起失步。可以将A1点附近起动的情况看作A2点起动的情况的上一阶段，因为当转子有反向初始速度时，在与速度反向的电磁转矩作用下，经过一段时间速度减小到零。转子反转阶段一定会造成转子位置远离平衡点，即θ0的绝对值增大。

由以上分析可知，步进电动机再次起动是否失步与系统频率和保持时间有关，系统频率即转子的振荡频率。保持时间Th满足：

(10)

式中：Tn为转子振荡周期。此时步进电动机再次起动时转子位置位于正向最大或者正向通过平衡位置，电机在此位置不容易失步。保持时间满足：

(11)

步进电动机再次起动时转子位置位于反向最大处或者反向通过平衡位置，电机在此位置易发生失步。

图4为动态起动导致失步的定转子磁场位置变化的仿真结果。磁场位置采用电角度，一个电周期是7.2°机械角度。控制器控制绕组电流通断，绕组电流产生的定子磁场在理想情况下是跳变的。在7 ms前电机正常运行，开环状态下转子磁场也能够较好跟踪定子磁场。7 ms时电机进入保持状态，保持时间为4 ms。再次起动时采用恒定1 kHz起动。步进电动机出现失步现象。可以看出，由于外部负载转矩和反向初始速度，转子磁场无法继续跟踪定子磁场。

图4 动态起动定转子磁场位置角

转子在保持状态下出现振荡现象。在保持时间为4 ms时起动，这时转子位置反向经过平衡点，具有很大的反向速度。前1.5个脉冲用于克服转子初速度，此后定子磁场与转子磁场位置角逐渐增大，电磁转矩也会逐渐减小。如图 5所示，当定转子磁场位置电角度差超过180°时，转子已经不在定子磁场正向控制范围，出现失步现象。

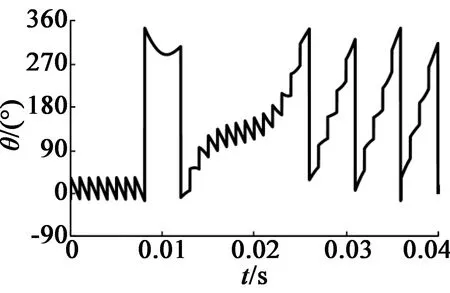
图5 动态起动定转子磁场位置角度差

3.2 降频起动导致失步

使用降频策略起动，可以减小起动时的定子磁场旋转速度，有效防止失步，但降低频率的设置不合适也会造成动态起动的失步。图6、图7为降频起动导致失步的定转子磁场位置变化仿真结果。12 ms时电机进入保持状态，保持时间为7 ms。再次起动采取降频起动，使定子磁场依次保持4 ms，3 ms，2 ms，1 ms。之后保持正常工作频率。起动频率从0.25 kHz，0.33 kHz，0.5 kHz，1 kHz上升。当电机保持时间结束时，转子处于反向位置最大的位置，第一个脉冲结束后已经将反向速度补偿完。在第二个脉冲时，由于定子磁场保持时间过长，转子磁场超前了定子磁场，电磁转矩变负，在第二个脉冲末端以及第三个脉冲时转子减速以及速度反向增大，第三个脉冲时转子速度反向，增加了第四个脉冲的拖动难度，导致后续的失步。

图6 降频起动定转子磁场位置角

图7 降频起动定转子磁场位置角度差

4 实验结果

实验选用的步进电动机为两相混合式步进电动机，该步进电动机参数如表1所示。

表1 步进电动机参数

步进电动机采取恒频起动策略，保持时间选择不合适会导致步进电动机失步，步进电动机转子磁场与定子磁场位置，两相电流如图8所示。其中转子磁场位置采用位置传感器测量得到，实验中位置传感器只用于测试，并未将位置信号反馈到控制系统中。为了直观看出定转子磁场位置的关系，定子磁场采用的是根据电压矢量得到的近似值，实际的定子磁场可以根据图8(b)中的电流曲线得到。

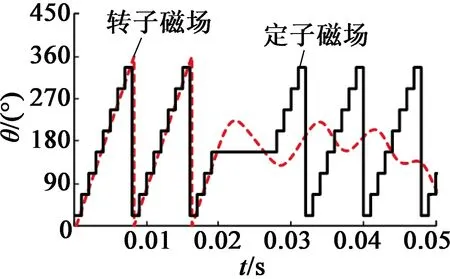
(a) 磁场位置曲线

(b) 电流曲线图8 保持阶段与起动阶段电流及磁场变化曲线(保持阶段为0.02～0.028 s，负载转矩TN=0.21 N·m)

保持阶段持续8 ms，在保持阶段结束时，步进电动机转子接近反转位置最大值，在此阶段采用恒频起动策略，转子由于存在反向初始速度以及初始位置滞后，导致转子磁场无法跟踪定子磁场，造成失步现象。实验结果也较好地证明了该失步分析方法的合理性。

5 失步解决措施

针对动态起动的失步情况，可以从两方面改善失步故障。

改善步进电动机的保持性能或者增加阻尼系数，可以增加步进电动机振荡衰减速度。对于多相步进电动机，在保持阶段，控制工作相绕组通路，非工作相绕组全部短路，可以有效改善步进电动机保持性能。

图9为非工作相绕组的H桥驱动器，其中T1～T4表示功率器件，D1～D4表示续流二极管，M表示非工作相绕组。

图9 非工作相绕组与H桥驱动器

通过控制上桥臂功率管T1, T2导通，下桥臂功率管T3, T4断开，使非工作相绕组处于短路状态，根据转子反电动势方向不同产生通路(1)和通路(2)。同理，将T3, T4导通，T1, T2断开效果相同。转子振荡时，在转子磁场的作用下，非工作相产生反电动势，进而产生电流。该电流产生的电磁转矩阻碍转子运动，加快转子振荡衰减。图10为非工作相绕组在保持阶段时开路和短路状态下，转子位置的对比图。短路状态下，转子衰减速度变快，有利于下次起动。

图10 非工作相绕组保持阶段开路与短路对比

图11为电机保持阶段非工作相绕组开路或短路对工作相的影响的仿真结果。非工作相绕组短路，电机转子在保持阶段振荡幅值更小，有利于下次起动；非工作相绕组开路，电机振荡幅值较大，在下次起动时，如果保持时间设置不合适，会造成电机失步。

图11 非工作相绕组开路与短路对电机失步的影响

另一方面，针对步进电动机的系统频率，确定步进电动机的保持时间和起动频率。让步进电动机在正向通过S点时起动，可以确保使用恒频策略起动时不发生失步。

由式(10)和式(11)可知，根据系统频率确定步进电动机保持时间，可以有效地防止失步。如图12所示，当系统频率ωn=561 rad/s，即步进电动机振荡周期Tn=11.2 ms时的步进电动机失步仿真结果，图12中，Th为保持时间。

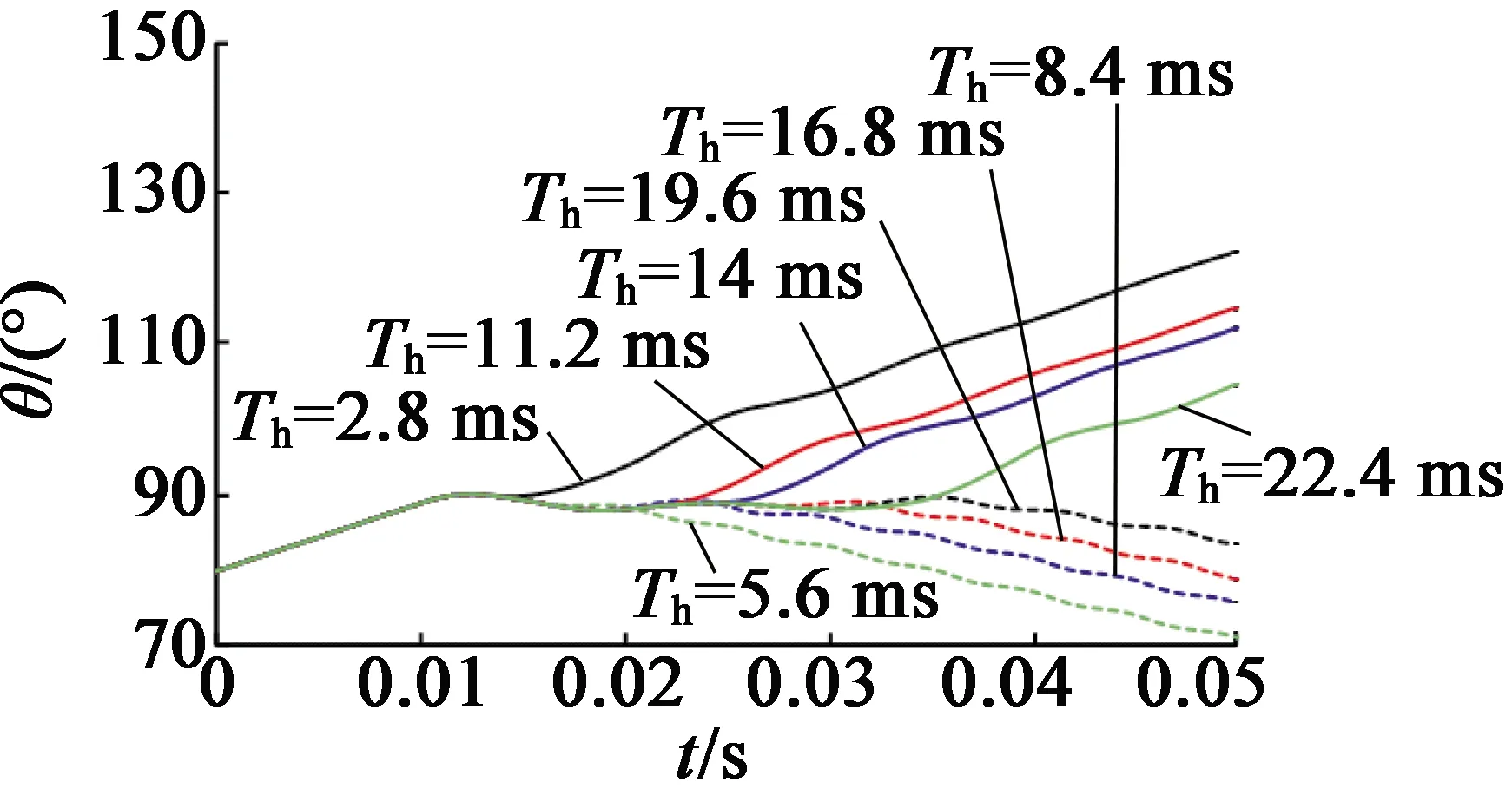
图12 保持时间对电机失步的影响

6 结 语

本文结合了步进电动机动态运动方程与矩角特性方程，较为详细地分析了步进电动机动态起动过程中的失步机理，解释了初始速度和初始位置的变化对步进电动机性能的影响。通过仿真与实验结果验证了该分析的合理性，并给出了相应的解决措施。该失步机理分析方法对制定频繁起停的步进电动机控制策略有着较高的参考价值。