复合材料层合板阶梯型胶接修补斜度有限元数值模拟研究

余 芬, 郭 拓, 刘武帅, 安伯宁, 邓殿凯, 何振鹏

（中国民航大学 航空工程学院，天津 300300）

与传统的金属材料相比，复合材料具有比强度高、比刚度高、质量轻、耐腐蚀等特点，在航空航天中得到广泛应用。复合材料结构在使用寿命期内，由于环境以及外部载荷条件等多种原因的影响，可能会发生损坏。为延长飞机服役寿命，需要更换或修理损坏的零件。复合材料传统修补方法主要有机械修补法和胶接修补法。机械修补法由于修补后增重较大、可设计性较差以及容易造成新的应力集中源等问题，对修补后的强度有较大的影响。胶接修补法除可以解决机械修补中存在的问题外，还具有操作简单、成本低以及修补后拥有较好的气动外形等优点。复合材料层合板在损伤之后所出现的应力集中现象会削弱层合板强度，导致无法满足现行工作需求，胶接修补后会提高材料的损伤容限和强度，使其达到预期工作效果。

目前，国内外已有很多学者在复合材料胶接修补方面进行研究。徐胜等[1]通过设计模拟机械损伤的复合材料修补试件，建立腐蚀修补模型进行径向拉伸实验，研究了补片的几何尺寸对修补的影响。苗学周等[2]以3D渐进损伤理论为基础，建立不同补片形状下的修补模型，并在单向载荷作用下，研究了补片形状及尺寸对胶接修补后强度的影响。刘斌等[3]建立复合材料损伤冲击模型，研究了低速冲击下复合材料层合板梯形斜面胶接的力学性能及损伤演化方式。章向明等[4]通过研究复合材料损伤力学特性，建立弹性力学模型，运用解析法及有限元法对双面加固单向加载平板的应力应变进行分析。朱书华等[5]建立了复合材料阶梯型胶接修补有限元模型，并讨论母板、胶层、补片三者之间的损伤扩展过程以及相互影响。李振凯等[6]建立分析复合材料双面贴补结构渐进损伤的有限元模型，提出了一种分析和预测在拉伸载荷作用下复合材料层合板双面贴补结构的极限承载能力的方法。Ghazali等[7-9]研究了边压载荷作用下原始、开孔和修复夹层板的力学性能，并进行有限元分析对修复后的夹层板进行强度预测。

目前，对复合材料层合板修补方法的研究文献较多，但研究改变开口斜度对修补效果影响的文献很鲜见。本研究基于渐进损伤模型和内聚力模型对阶梯型胶接修补的复合材料层合板进行模拟，首先将数值模拟得到的位移载荷曲线与实验进行对照来验证模型的正确性，进一步研究不同开口斜度对胶接修补后复合材料层合板强度恢复率的影响，将模拟得出的损伤扩展情况与实验结果进行对照，分析其损伤机理。

1 典型复合材料阶梯型胶接修补结构

复合材料层合板阶梯型胶接修补工艺方式如图1所示，其修补过程通常是借助机械工具将层合板发生损伤部位逐层打磨去除，最终形成阶梯型。清理待修补区域后，采用热补仪或真空袋工艺，将层合板与补片通过胶接方式粘接固化成型以完成修补。为避免修补区域接触溢胶情况发生，本研究中将损伤区域打磨为圆形，使胶层有效粘合层合板与补片。阶梯型胶接修补层合板分8层，单层厚度0.12mm，铺层角度为[+45/0/-45/90]s，补片分9层，顶层为额外铺层，角度为0°，其余8层角度与母板一致，分别为[+45/0/-45/90]s，层合板与补片间存在厚度为0.1mm的胶层，修补截面以及铺层角度如图2。由于在复合材料层合板阶梯型胶接修补分析中考虑到修补斜度问题，需要给予斜度工程定义，修补斜度（Slope）定义为层合板单层阶梯工艺切口厚度（h）与切口长度（l）的比值，反映了工艺切口厚度对切口长度的倾斜程度，具体示意如图3。其表达式为：

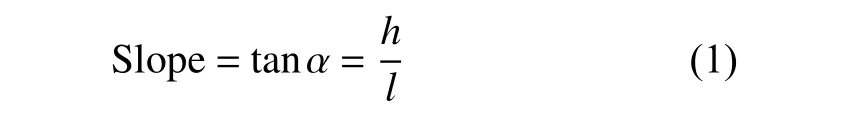
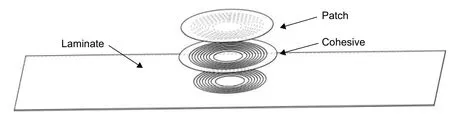
图 1 复合材料层合板阶梯型胶接修补模型Fig. 1 Model of step-type glue repairing for composite laminate

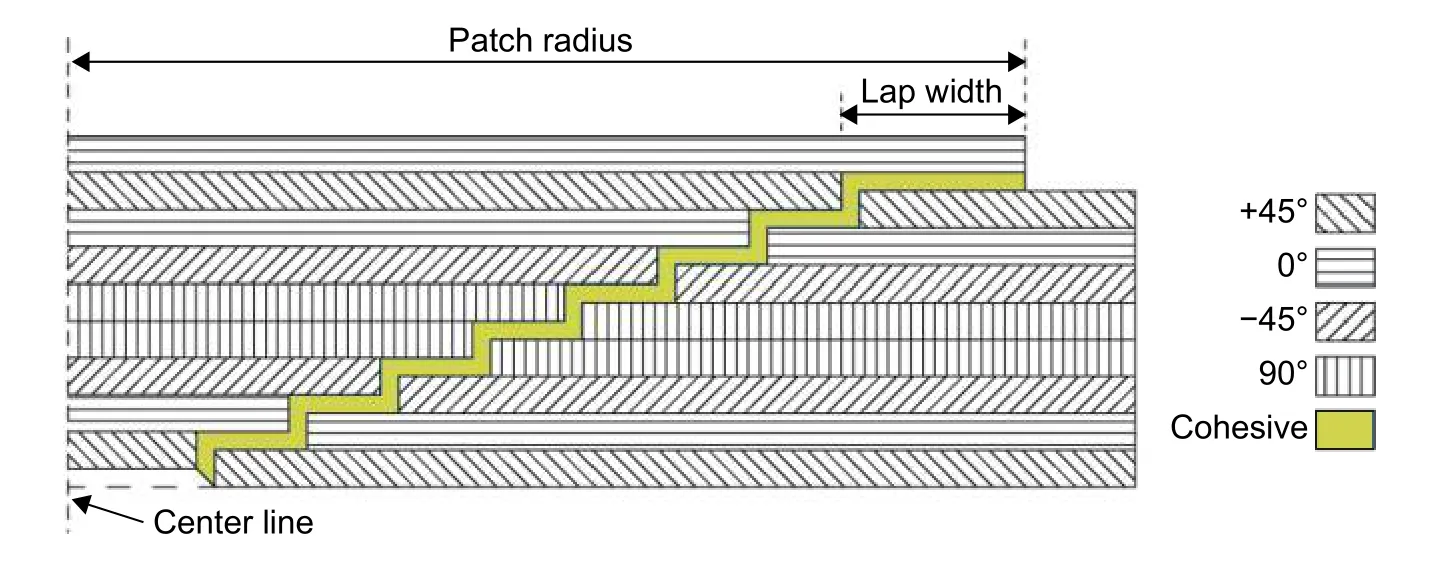
图 2 修补截面和铺层角度示意图Fig. 2 Schematic diagram of repaired section and lay-up angle

图 3 待修补层合板打磨方式及斜度示意图Fig. 3 Schematic diagram of grinding method and slope of composite material to be repaired

由文献[10]可知，修补斜度大于1∶10的试件在单向拉伸载荷作用下表现出相近的特性。修补斜度的大小决定了胶接接头的有效胶接长度以及修补后补片的承载能力，对修补质量有至关重要的影响。本研究选择比较有区分度的四种斜度：1∶10、1∶15、1∶20、1∶25进行有限元仿真分析，层合板打磨方式如图3。对于修补结构的斜度研究，由于涉及胶层和层合板的损伤机理问题，需要针对修补结构中母板、胶层、补片之间的连接特性以及胶接接头的有效胶接长度等问题选取合适的损伤判据并修改刚度退化模式。考虑边界条件非线性、材料非线性以及模型收敛性问题，需要针对修补模型编写VUMAT子程序定义材料失效判据并选取合适的求解器以完成分析。

2 阶梯型胶接修补斜度研究的有限元方法

ABAQUS软件中的Explicit求解器在准静态静力拉伸分析中表现优越，现已广泛应用于准静态问题[11]。Explicit求解器是显式的求解方程组，以相对较小的时间增量迭代推出结果，同时不需要考虑收敛问题。本研究中母板、胶层以及补片三者之间的接触问题属于边界条件非线性问题；积分点应力满足失效判据后，材料属性根据刚度退化模型进行折减的现象属于材料非线性问题。引入混合损伤模式下双线性Cohesive单元可以较为准确地模拟胶层受载后的应力分布情况，对于研究不同斜度下胶接接头对修补模型的影响至关重要。因此，结合Hashin失效准则以及刚度退化方式的VUMAT子程序配合使用Explicit求解器是较为合适的选择。

2.1 结构参数

本研究算例基于文献[12]中COOK BM的实验，对尺寸为572 mm × 133 mm × 0.96 mm的复合材料层合板进行阶梯型修补仿真分析，母板和补片材料均选用IM6/3501-6碳纤维环氧预浸料，材料参数见表1。胶层材料选用型号为FM300-05M的胶黏剂，材料参数见表2。不同斜度对应的母板及补片开口半径见表3及表4。

表 1 IM6/3501-6复合材料属性参数[12]Table 1 Attribute parameters of IM6/3501-6 composites[12]

表 2 FM300-05M胶层材料参数[12]Table 2 Material parameters of FM300-05M adhesive layer[12]

表 3 不同斜度下母板修补处打磨半径Table 3 Grinding radius of composites under different inclination angles

2.2 有限元建模方法

基于Abaqus软件建立复合材料层合板阶梯型胶接修补分析模型，有限元模型和边界条件如图4所示。边界条件为左侧约束三个平动位移自由度，右侧施加5 mm的轴向拉伸位移载荷。考虑到层合板中间部位由于开孔导致的应力集中现象，为保证分析的准确性，在仿真分析中对层合板开口处进行网格加密处理并设置单元类型为C3D8R。选用Cohesive单元进行胶层模拟，单元类型为COH3D8，补片-胶层-母板之间选用Tie绑定约束。模型的建立以及分析参数设置完成之后，需要针对材料的本构关系以及损伤演化过程编写VUMAT子程序，从而实现层合板的单向拉伸极限强度分析。

表 4 不同斜度下补片打磨半径Table 4 Patch grinding radius at different inclination angles

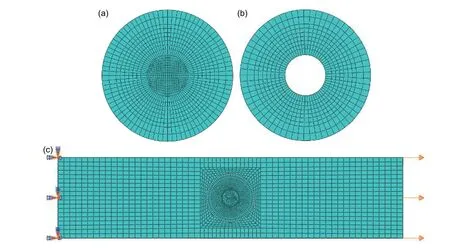
图 4 有限元模型 （a）补片网格；（b）胶层网格；（c）整体网格Fig. 4 Finite element model （a） patch grids；（b） cohesive grids；（c） model grids

2.2.1 渐进损伤模型

目前，常用的失效应力准则主要有最大主应力失效准则，Hashin失效准则，Hoffman失效准则，Tsai-Wu张量理论，Tsai-Hill失效准则[13]。对复合材料胶接修补而言，因Hashin失效准则编写程序简单且能够准确预测复合材料层合板胶接修补后的极限承载能力，故而选择Hashin失效准则进行失效分析。Hashin失效准则的具体公式如下：

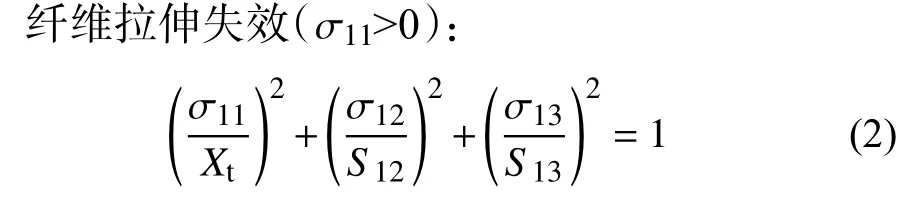
式中： σ11， σ12， σ13为 常规的积分点应力； S12， S13为单个铺层面内剪切强度； Xt为纤维方向拉伸强度。

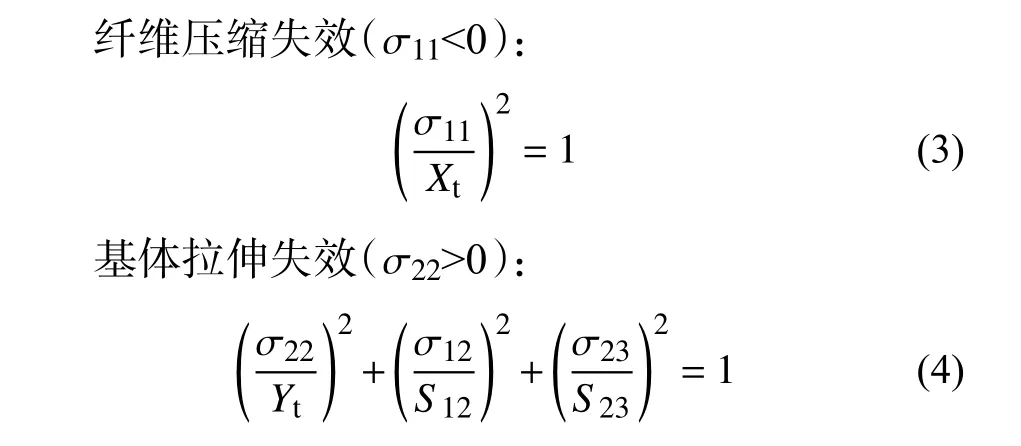
式中： σ22， σ23为 常规的积分点应力； S23为单个铺层面内剪切强度；Yt为垂直纤维方向拉伸强度。

式中： Xc为纤维方向压缩强度。

根据上述Hashin失效准则可知，随着层合板各个方向上的应力逐渐增大，其内部积分点处出现损伤，材料的属性参数会发生折减，导致初始弹性矩阵无法准确预测变化，因此需要引入刚度退化模型判断单元破坏模式来修正材料的基本参数。为避免单元失效后发生畸变进而导致计算中止的问题，在Liu等[14]的参数退化方式上加以修正以适用于本研究中材料的本构关系，将材料失效后参数退化为0的部分，修改为退化之前的0.1倍，参数退化方式如表5所示。

表 5 刚度退化方式Table 5 Stiffness degradation mode

2.2.2 胶层内聚力模型

在受到位移载荷作用时，母板与补片之间的胶层也会因超过其强度极限而破坏，所以胶层力学特性的模拟对于模型的分析显得尤为重要。本研究中层合板与补片之间的胶层选用内聚力模型模拟，ABAQUS软件提供了双线性本构关系的Cohesive单元，本构关系具体表达式如下：

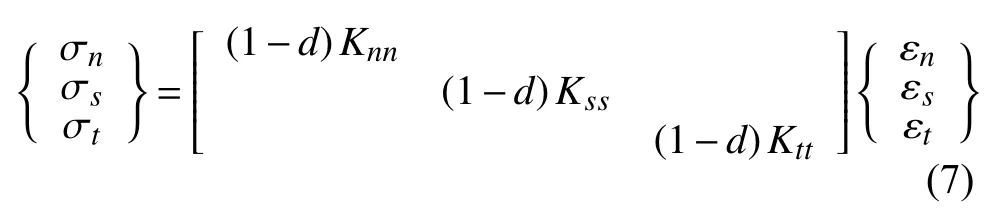
δn、 δs、δt分别为Cohesive单元节点法向和两个切向相对位移； Enn、 Ess、 Ett为内聚力单元三个方向弹性模量；T0表示Cohesive单元的初始厚度。

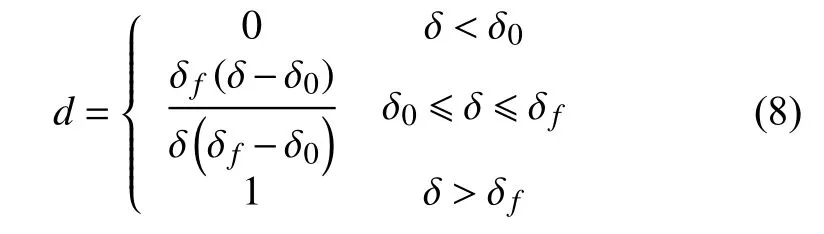
式中： δ0表示初始损伤时的位移；δf表示最终失效时的位移。

选择二次应力准则作为损伤起始判据，其表达式如下：

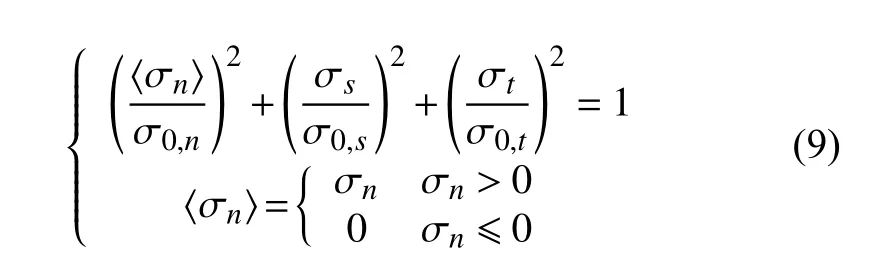
σ0,n， σ0,s， σ0,t表示内聚力单元三个方向上的损伤起始应力， 〈 σn〉表示厚度方向上压应力不会引起损伤。

选择基于能量的B-K准则作为损伤扩展准则，其表达式如下：

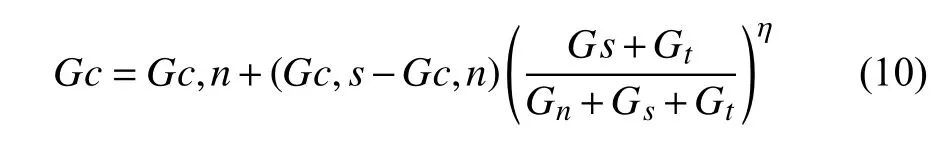
式中： Gc 为 等效断裂韧度； Gc,n和 Gc,s分别为Ⅰ型裂纹和Ⅱ型裂纹断裂韧度。Gn为Ⅰ型能量释放率；Gs和 Gt为Ⅱ型能量释放率。η是与材料相关的系数，碳纤维复合材料一般取值2～3[15]，本研究取η=2。

混合损伤模式下Cohesive单元的本构方程如图5。

图中： σ0,n， σ0,s， σ0,m分别为法向模式，切向模式和混合模式下损伤起始应力。 δf,n， δf,s， δf,m分别为法向模式，切向模式和混合模式下失效位移。

2.2.3 渐进损伤分析流程

基于ABAQUS有限元软件，通过编写VUMAT子程序定义复合材料失效准则以及刚度退化方式来实现层合板修补结构渐进损伤性能分析，VUMAT子程序在求解过程中需要在软件中读取模型参数并将最终计算结果输入至软件中以完成整个分析，计算流程如图6所示。

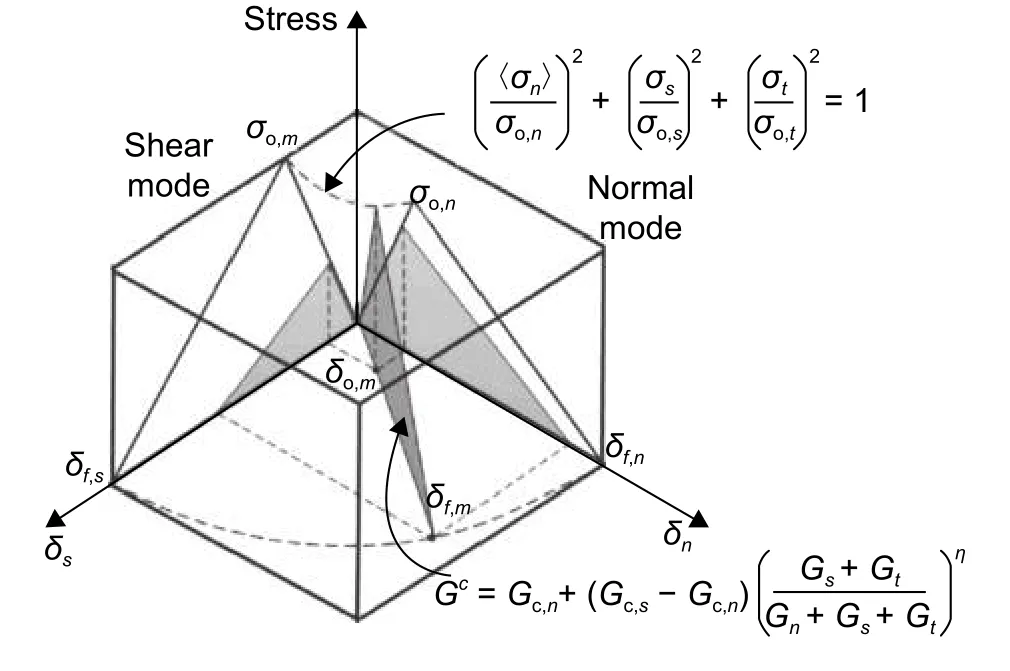
图 5 混合损伤模式下Cohesive单元本构关系Fig. 5 Cohesive element constitutive relation under hybrid damage model

图 6 VUMAT子程序渐进损伤分析流程图Fig. 6 Flow chart of VUMAT subroutine progressive damage analysis

3 有限元验证与结果讨论

3.1 有限元验证

基于本研究提出的对层合板进行阶梯型胶接修补后的极限承载强度预测问题，首先与文献[12]中的实验结果进行对比，文献中无损层合板的极限承载强度为68692 N，损伤后的极限承载强度为27745 N，胶接修补后的极限承载强度为60137 N，实验结果表明，以无损层合板的极限承载强度为标准，从受损层合板的极限承载强度占比40.4%到胶接修补后的极限承载强度占比86.5%，足以证明胶接修补后层合板的极限承载能力有了相当的改观。

图7为实验测得的极限载荷与文献[5，16]及本研究数值模型预测的位移载荷曲线对比图。由图7可知，位移加载初期，预测的位移载荷曲线斜率基本一致，表明材料在未发生损伤时子程序中进行应力更新过程的正确性。曲线的最高点与实验值接近，表明选择的失效判据和刚度退化模型的正确性。图7中位移载荷曲线的极限强度值和与实验值的相对误差如表6所示。

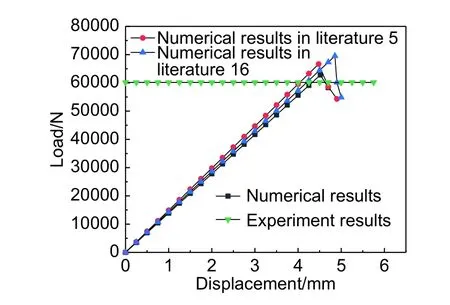
图 7 层合板修补后位移-载荷曲线对比Fig. 7 Comparison of displacement-load curve after laminate repair

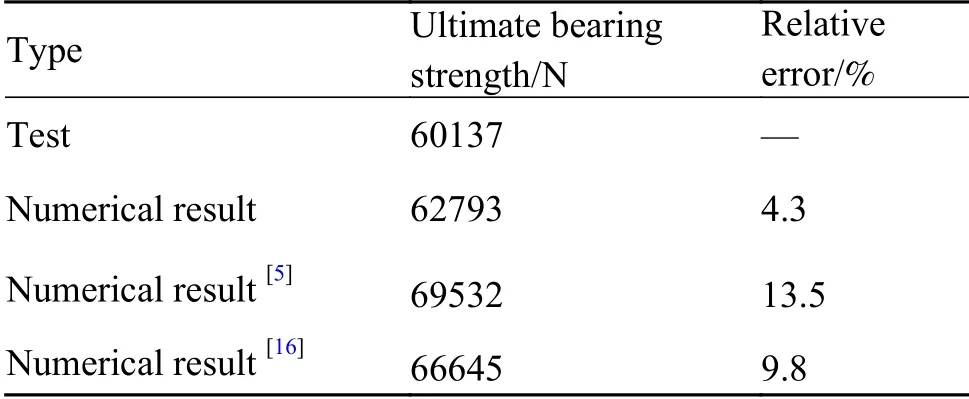
表 6 修补后极限承载强度与相对误差对比Table 6 Comparison of ultimate bearing strength and relative error after repair

由表6可知，文献[5]中极限承载强度为69532 N，失效位移4.854 mm，与实验结果的相对误差为13.5%；文献[16]中极限承载强度为66645 N，失效位移4.475 mm，与实验结果的相对误差为9.8%；本研究修补后的极限承载强度为62793 N，失效位移4.515 mm，与实验结果的相对误差为4.3%。

3.2 斜度对修补模型极限承载能力的影响

图8为不同斜度修补后层合板的极限承载强度对比。由图8可知，斜度为1∶10的时候斜率最大，表明修补斜度越大，极限承载强度的增量受材料刚度影响越大，极限承载强度随斜度的减小而增加。4种斜度的失效位移、极限载荷及修复率如表7所示。由表7可知，斜度为1∶10时的极限承载强度为49046 N，最大拉伸位移为3.253 mm，与无损层合板实验结果相比修复率为71.4%。斜度为1∶15时的极限承载强度为57083 N，极限拉伸位移为4.126 mm，修补效率达到83.1%。斜度为1∶20和1∶25时的极限承载强度相差不大，分别为62793 N以及62647 N，最大位移载荷均为4.515 mm，平均修补效率达到91.3%。

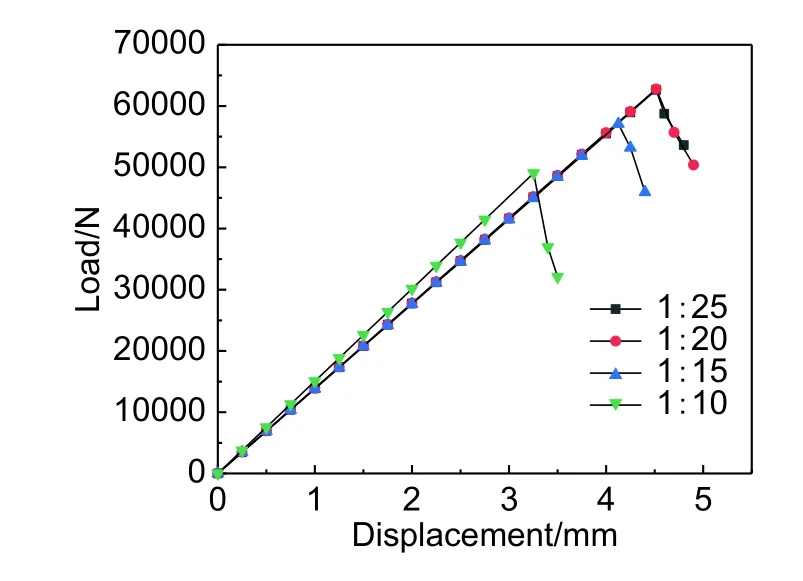
图 8 不同斜度下载荷-位移曲线Fig. 8 Load-displacement curve at different slopes

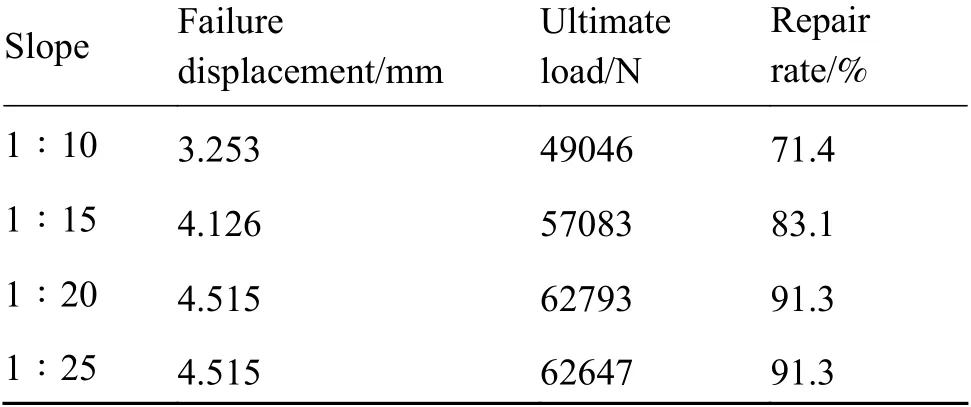
表 7 不同斜度的失效位移、极限载荷及修复率Table 7 Failure displacement，limit load and repair rate of different slopes

结果表明，随着修补斜度的减小，模型的极限承载能力逐级增加。在修补斜度到达1∶20和1∶25时，虽然斜度有较为明显的减小，但修补效率并未有过大的提升。从工艺以及经济性的角度考虑，对于拉伸载荷承载能力要求较高的修理件，1∶20的斜度在修补工艺上较为合适。

3.3 失效模式及损伤演化

修补后的复合材料层合板在单向拉伸载荷作用下的传力路径包括两部分[17-18]，一是由母板修补处传递至未损伤部分，二是通过胶层传递至补片，以缓解由于层合板损坏引起的应力集中。图9为试件在位移载荷作用下的最终破坏形式。图9表明，由于单向位移载荷的作用，修补区域的层合板与补片粘连失效。随着胶层损伤逐渐扩展，层合板修补增强能力下降，胶层完全失效后，层合板沿位移载荷垂直方向断裂。

图 9 试件最终破坏形式[13]Fig. 9 Final failure form of the test piece[13]

图10为有限元仿真分析得到的胶层损伤扩展过程，SDEG表示Cohesive单元损伤的变量，SDEG值为1时表示该单元失效，为0时表示单元未失效。图10（a）为胶层的损伤起始状态，图中表明，由于材料刚度特性的影响，拉伸起始阶段，胶层损伤并不明显，首先发生在连接补片与层合板0°铺层最大半径处，但随着位移载荷的逐步增加，额外铺层的承力作用减小，结构变形加剧，胶层损伤逐渐从最小开口半径处向垂直于施载方向的自由边界扩展，如图10（b）所示，最终扩展至自由边界脱离层合板而失效，如图10（c）所示，失效情况与实验结果相吻合。

由于层合板单层厚度固定，随着斜度的减小胶接面积逐渐增大。图11（a）为层合板斜度为1∶10所对应的胶层应力分布图，此时最大应力发生于胶层最大半径外缘，且应力主要集中于垂直施载方向，对于缓解应力集中问题效果较差；图11（b）为层合板斜度为1∶15所对应的胶层应力分布图，图中表明，胶层应力承载范围逐渐向平行于施载方向扩展，在一定程度上缓解了应力集中问题；图11（c）和（d）分别为斜度为1∶20和1∶25所对应的胶层应力分布，图中表明，随着胶接接头有效长度的逐渐增加，胶层最大半径外缘应力承载能力增加，应力承载区域逐渐扩展至整个胶层，有效缓解了应力集中问题，从而推迟补片与母板的脱粘，提高修理结构强度。

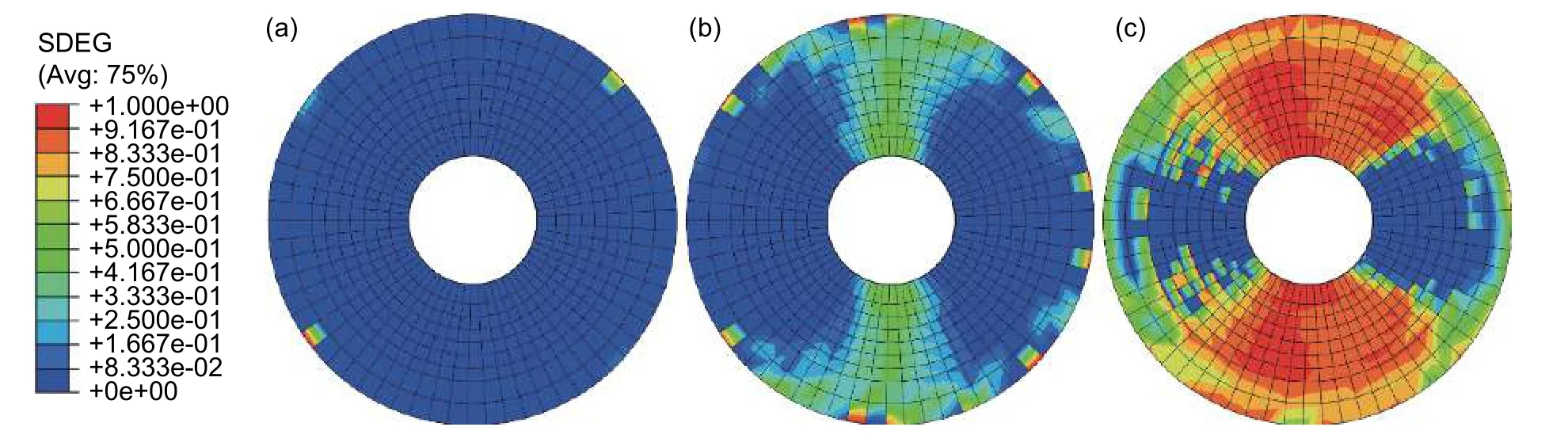
图 10 胶层损伤失效的起始与扩展 （a）损伤起始；（b）损伤扩展；（c）最终失效Fig. 10 Initiation and expansion of the damage failure of adhesive layer （a） damage initiation；（b） damage extension；（c） final failure

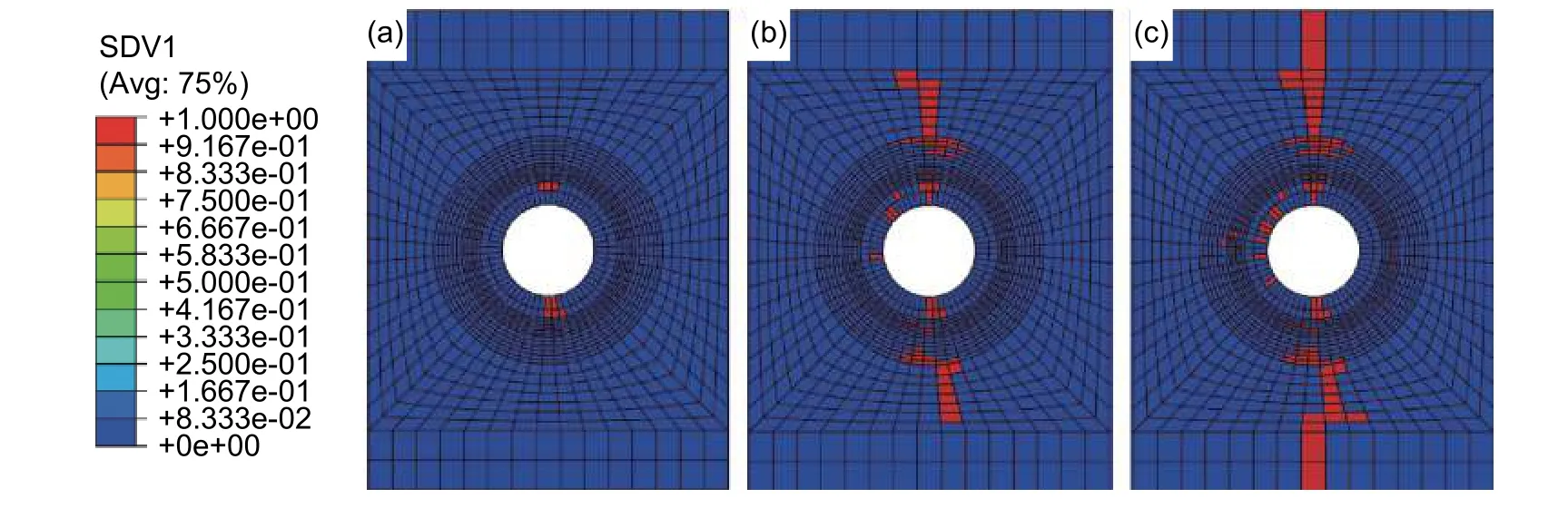
图 12 层合板纤维拉伸失效的起始与扩展 （a）损伤起始；（b）损伤扩展；（c）最终失效Fig. 12 Start and expansion of laminate fiber tensile failure （a） damage initiation；（b） damage extension；（c） final failure

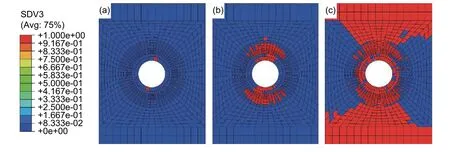
图 13 层合板基体拉伸失效的起始与扩展 （a）损伤起始；（b）损伤扩展；（c）最终失效Fig. 13 Starting and expanding of tensile failure of laminate substrate （a） damage initiation；（b） damage extension；（c） final failure

图12和图13分别给出了层合板纤维和基体在轴向拉伸载荷作用下的损伤过程。SDV1表示层合板纤维拉伸失效的状态变量，当SDV1值为1时表示单元失效，为0时则表示单元未失效，即在图中失效单元呈现出红色，未失效单元呈现出蓝色。由图可知由于0°铺层在拉伸载荷作用下的刚度影响，层合板的纤维损伤起始于开口半径较小的0°铺层处，如图12（a）所示，并逐级向外扩展直至自由边界。SDV3表示层合板基体拉伸失效的状态变量，基体拉伸失效的损伤起始与纤维拉伸失效不同，基体损伤首先会出现在层合板最小半径处，如图13（a）所示。然后向周围扩展直至自由边界，此时层合板因无法继续承载而沿垂直于位移载荷方向断裂失效。研究结果表明，在单向拉伸载荷作用下，层合板纤维损伤主要受0°方向载荷影响，层合板基体损伤主要受90°方向载荷影响，失效单元沿垂直于位移载荷方向扩展。

4 结论

（1）建立的渐进损伤模型预测的极限拉伸强度与实验进行对照，误差小于5%，验证所建立模型的正确性。

（2）研究不同斜度对胶接修补后极限拉伸强度的影响，结果表明：当修补斜度为1∶15时，修补效率达到83.1%，修补效率已经满足大多数修补要求，随着斜度的逐渐减小，修补效率逐渐增加，当斜度为1∶20和1∶25时，极限承载强度的增加不明显。因此，对于拉伸载荷承载要求较高的修理件，选择1∶20的斜度在层合板胶接修补工艺上较为合适。

（3）材料失效及破坏模式与实验失效情况吻合，损伤部位为应力集中区域，胶接接头的有效胶接面积随斜度的减小而增大并在一定程度上缓解了应力集中。基体拉伸失效首先发生在损伤区域最小半径处，并沿垂直于施载方向扩展；纤维拉伸失效首先发生在0°铺层处，并沿垂直于施载方向扩展。