“五家共井”问题的算法实现

程璞

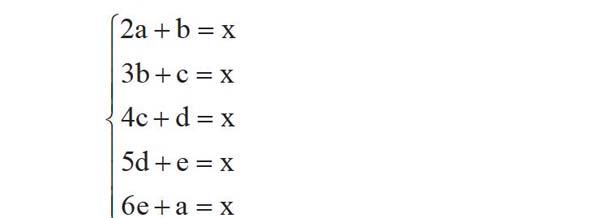
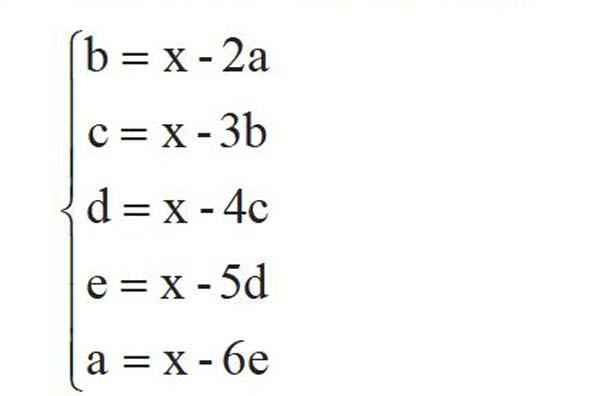
摘 要：我国是最早研究不定方程的国家之一，最古老的不定方程问题是《九章算术》中的“五家共井”问题。本文通过对“五家共井”问题的算例分析、算法描述及上机实践，将这一古老数学问题与计算机技术相结合，让学生感受算法学习的巨大作用。

关键词：数学;不定方程;算法

不定方程是数学数论的一个分支，它有着悠久的历史与丰富的内容。所谓不定方程是指解的范围为整数、正整数、有理数或代数整数的方程组，其未知数的个数通常多于方程的个数。我国是最早研究不定方程的国家之一，最古老的不定方程问题是《九章算术》中的“五家共井”问题，比古希腊丢番图方程早300多年，继《九章算术》之后的《张丘建算经》中对不定方程的论述体现了很高的水平，书中的“百鸡问题”是一个影响至今的不定方程问题，另外，《孙子算经》中的“物不知数”问题等都是在这方面的杰出成果，体现了中国古代数学的伟大成就，是世界数学史中的瑰宝！

“物不知数”与“百鸡问题”在《普通高中课程标准实验教科书（苏教版）》（必修3）中以例题或习题的形式出现，下面以《九章算术》中的“五家共井”问题为例谈不定方程的算法实现。

问题：“今有五家共井，甲二绠（提水用的井绳）不足如乙一绠，乙三绠不足如丙一绠，丙四绠不足如丁一绠，丁五绠不足如戊一绠，戊六绠不足如甲一绠，各得所不足一绠，皆逮，问井深绠长几何。”

这道题译成白话文是：有一口甲、乙、丙、丁、戊五家共用的水井，不知道井有多深。现在用这五家的提水绳来测量井深，若用甲提水绳的2倍测，还差乙提水绳的长;用乙提水绳的3倍测，还差丙提水绳的长;用丙提水绳的4倍测，还差丁提水绳的长;用丁提水绳的5倍测，还差戊提水绳的长;用戊提水绳的6倍测，还差甲提水绳的长。问：井深与提水绳长各是多少？

下面我们从以下几个步骤探析改题的算法解决过程。

1 感悟算理——“算理”是学生走向“算法”的桥梁

算理顾名思义是实施计算方法的原理，只有把握了算理，才能据此寻求算法。若只告诉学生怎么算，忽略理解算理的环节，如同建造“空中楼阁”，没有稳固的根基容易使学生“知其然而不知其所以然”，也就失去了独立思考和深层感悟的宝贵机会。

这题学生很自然地想到列方程解决，可设井深为x，甲、乙、丙、丁、戊的提水绳长分别为a、b、c、d、e，由五组数量关系列五个方程：

由于未知数的个数多于方程的个数，可以取无数组解，但常识告诉我们，井深x一般在50寸到1000寸之间，且a、b、c、d、e均为正整数，故方程组有有限组解。

据此产生如下算法：将x看成“已知数”，用可能的x值（50到1000间的正整数）——代入试验，若a、b、c、d、e均为正整数，则这组数为方程组的解。由于

因此，只需判断其中一个未知数为正整数，即可确定其它未知数均为正整数。这里取a为待检变量，故需找到x与a之间的关系，将方程化简为265x=721a

2 描述算法——找准“算理”与“算则”的结合点

在构思了算法之后，必须清楚准确的将所设计的求解步骤记录下来，即描述算法，常用的描述算法的方法有自然语言，流程图，程序设计语言和伪代码等。自然语言通俗易懂，直接明了;流程图直观形象，能体现算法过程的结构特征，但除了非常简单的算法外，这种描述方法使用起来非常不方便;伪代码将各个流程图的结构用接近程序语言的算法语句表述，是介于自然语言和程序设计语言之间的算法，它采用某一程序设计语言的基本算法，操作指令可以结合自然语言设计。至于算法中自然语言成分的多少，取决于算法的抽象級别，抽象级别高的伪代码自然语言多一些。它极小化了描述算法的不必要的技术环节，是比较合适的描述算法的方法。

3 上机实践——检验算法的“试金石”

针对上面的算法过程，接下来必不可少的步骤就是上机检验，若发现问题，可及时修改，指导运行处正确结果。这样不仅能够验证程序的正确性，也能提高学生的实际操作能力，更深刻地感受算法的特点，体会算法与计算机天然内在的联系。

《普通高中数学课程标准（实验）》中指出：“本模块中的算法内容是将数学中的算法与计算机技术建立联系，形式化地表示算法，在条件允许的学校，使其能在计算机上实现。”算法学习可以与计算机等信息技术课程很好的联系在一起。同时，通过计算机实现算法，解决数学问题还可以让学生看到算法的可行性，应用性，激发学生学习算法的积极性。

参考文献：

[1] 苏教版高中数学教材编写组.普通高中课程标准实验教科书（必修3）[M].南京：江苏凤凰教育出版社，2019.