环形引射器两相流动数值模拟

吴薇梵，王占林，孔凡超，刘瑞敏，李 茂

(1.北京航天试验技术研究所，北京 100074； 2.北京市航天试验技术与装备工程技术研究中心，北京 100074)

0 引言

引射器是一种利用高速射流来抽吸低压流体的设备，它没有运动部件，结构简单，工作可靠，且对被抽气体无严格要求，应用于制冷、冶金、石油化工以及航空航天等多个领域。在上面级火箭发动机的研制过程中，需要通过高空模拟试验研究发动机的高空工作状态，引射器作为一种抽真空设备，在高空模拟试验中得到广泛使用。

国内外研究人员对引射器进行了大量的数值模拟研究[1-11]和试验研究[12-18]，分别研究了进出口工况及引射器结构尺寸等对引射器性能的影响，但是对无负载(零二次流)引射器的研究较少。还有研究人员对引射过程中水蒸气凝结相变现象进行了数值模拟研究[19-21]，但是目前的数学模型与实际情况还存在较大差距。

引射器流场复杂，涉及超音速流动、激波等多种复杂现象，同时，由于超音速的影响，蒸汽引射器内还可能存在气液两相流。一维引射器理论无法求解出流场内的详细结构，试验测量花费高且难以捕捉流场细节，因此，CFD数值模拟成为一种研究引射器内部流场的重要手段。在上面级火箭发动机进行高空模拟试验时，为较好地获得发动机的高空模拟特性，创造较低的真空压力是必要的。本文通过数值模拟，在两相流动的基础上分析零二次流环形蒸汽引射器入口工况及结构尺寸对极限真空压力的影响，旨在提高引射能力，降低真空压力。

1 物理模型与数值方法

1.1 物理模型及网格

某型上面级氢氧发动机环形蒸汽引射器结构如图1所示。

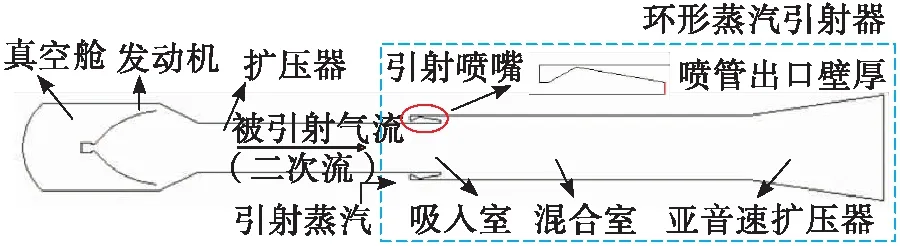
图1 环形蒸汽引射器结构图

其中引射器长为10.9 m，引射喷嘴环缝截面积为3.8×10-5m2，引射喷嘴出口壁厚为0.05 m，混合室直径为1.104 m，扩张段出口直径为1.561 m。蒸汽由水/液氧/酒精蒸汽发生器提供。在进行网格无关性分析后，计算网格取20万个，采用结构网格，网格示意图如图2所示。

图2 计算区域网格

1.2 控制方程、湍流模型及计算方法

本文采用仿真软件Fluent对在发动机启动前的环型蒸汽引射器零二次流的流场进行模拟，控制方程为稳态二维轴对称雷诺平均Navier-Stokes方程，湍流模型选用Realizablek-ε模型。采用Coupled算法耦合求解，连续方程、动量方程和能量方程用二阶迎风格式进行离散。

1.3 物性参数及边界条件

引射喷嘴入口边界条件采用压力入口，设定入口总温为530 K，总压为1.85 MPa，蒸汽化学成分及各成分占比见表1；二次流入口设为固壁；引射器出口采用压力出口，给定出口压力为大气压。在Fluent中开启组分输运，混合气体的密度采用真实气体的Real-Gas-Soave-Redlich-Kwong三参数状态方程进行计算。

表1 环形引射器蒸汽化学成分

1.4 相变模型

蒸汽在引射器内会发生超音速流动，水蒸气加速膨胀降温降压，可能会有部分水蒸气越过气液饱和线变为液相，导致引射器内气液两相流共存。不考虑液滴在超音速流动过程中的成核及生长过程，采用水蒸气平衡凝结相变模型，假设水蒸气状态越过气液饱和线后立即凝结为液相水。

2 计算结果及分析

2.1 数值模拟与试验数据对比

环形蒸汽引射器的10次典型试验结果如图3所示，极限真空压力px即真空舱内压力，其平均值为12.60 kPa。

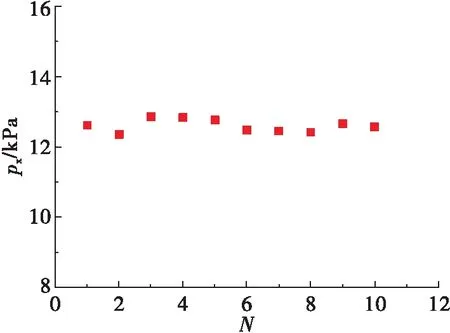
图3 环形蒸汽引射器典型试验结果

不考虑水蒸气相变，数值模拟所得真空压力为8.65 kPa，与试验数据的误差为31%；加入水蒸气相变模型，数值仿真后真空压力为12.15 kPa，与试验数据的误差小于5%。因此认为，在引射器内部存在的跨音速流动中，蒸汽两相流会对数值模拟计算结果产生一定的影响，下文的数值模拟过程中均引入水蒸气平衡凝结相变模型，考虑蒸汽两相流的存在。

2.2 入口工况的影响

引射蒸汽入口的温度和流量是由上游蒸汽发生器决定，蒸汽入口压力由入口温度和流量决定，与温度的开方及流量均成正比。本节将研究入口工况对极限真空压力的影响，通过分析仿真结果，给出降低真空压力的建议。

2.2.1 入口压力的影响

保持引射蒸汽入口总温不变，改变蒸汽入口流量，蒸汽入口总压发生变化，数值模拟结果如表2所示。

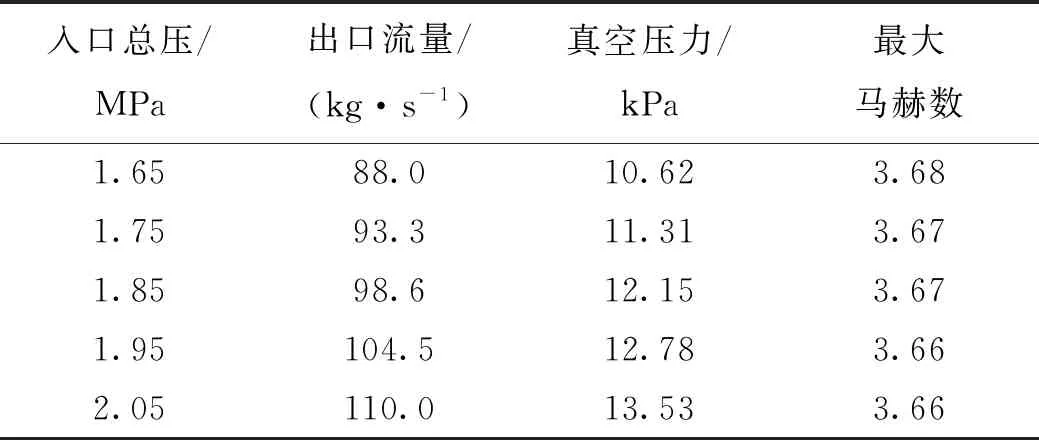
表2 不同入口总压下的计算结果

由表2可知，随着引射蒸汽入口流量增大，入口总压也增大，真空压力随之升高，但是真空压力与入口总压的比值及流场内最大马赫数基本无变化。结合图4和图5，对比不同入口总压下的数值模拟结果可以看到，流场内马赫数的大小及液相水体积分数的分布基本相同，只是下游激波的位置有细微差别，随着入口总压升高，激波串向下游推进。从总压曲线图中可以看出，随着入口总压增大，要保证出口总压一致，就要增大流动过程中的总压损失，而经过的激波道数越多，总压损失越大，因此入口总压越大，激波道数越多，激波串越靠近下游出口。可以认为，对于无二次喉道引射器来说，若想得到较低的真空压力，在保证引射器正常启动及入口总温不变的情况下，引射蒸汽入口总压越低越好。降低引射蒸汽入口总压，可以通过减少蒸汽流量来实现。

图4 不同入口总压下的马赫数分布

图5 各参数沿引射器轴线的变化

2.2.2 入口温度的影响

保持引射蒸汽入口流量不变，改变入口总温，数值模拟结果如表3所示。

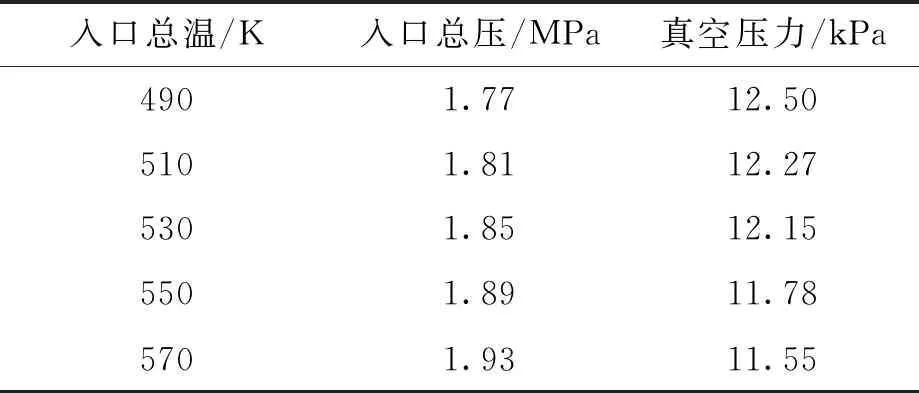
表3 不同入口总温下的计算结果

结合表3、图6和图7可以看到，随着入口总温提高，入口总压随之增大，流场中温度升高，温升在扩张段比较明显；正激波位置更靠近出口，流场内的马赫数逐渐增大，真空压力随之降低，液相水体积分数逐渐减少。水蒸气流经喷嘴时发展为超音速流动，气流加速膨胀降温降压形成液相水，由于温降有限，蒸汽温度越高，产生冷凝的蒸汽量减少，流场中液相水减少，从而导致流场中气流速度增大，引射器抽吸能力增强，真空压力降低。可以认为，若想得到较低的真空压力，在保证引射器正常启动及引射蒸汽流量不变的情况下，蒸汽入口总温越高越好。

图6 不同入口总温下的液相水体积分数分布

图7 各参数沿引射器轴线上的变化

2.3 几何参数的影响

下面将通过改变引射喷嘴出口壁厚和混合室直径，分析引射器几何参数对极限真空压力的影响。

2.3.1 引射喷嘴出口壁厚的影响

喷嘴出口壁厚是指环形引射器引射蒸汽出口与被引射气流入口之间的壁厚。图8给出了环形引射器出口壁厚局部放大图及其网格分布，在初始壁厚为0.05 m的基础上，改变喷嘴出口内径，喷嘴出口截面积也会有细微变化，将壁厚减小为0.03、0.015、0 m，引射器的其余几何参数及边界条件均不变。

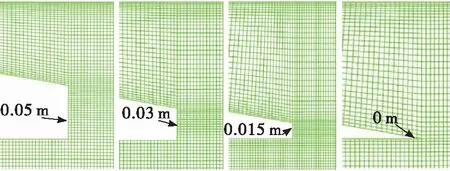
图8 不同引射喷嘴出口壁厚的局部放大图

表4给出了基于不同引射喷嘴出口壁厚下的计算结果。结果表明，随引射喷嘴出口壁厚减小，真空压力降低。根据图9喷嘴出口速度分布，分析认为，由于壁厚减小，在壁厚处气流产生的回流区减小，蒸汽受到的扰动减弱，对舱内气体的引射能力增强，从而真空压力降低。因此，尽管在实际制造中引射喷嘴出口壁厚不可能为零，但是尽可能地减小喷嘴出口壁厚，对降低真空压力有一定帮助。

图9 引射喷嘴出口处速度分布

表4 不同喷嘴出口壁厚下的计算结果

2.3.2 混合室直径的影响

引射器极限真空理论计算公式为

(1)

(2)

式中：Am为混合室截面积；At为喷嘴环缝截面积；Mm为混合室马赫数；k为比热比；px为吸入室静压；p*为吸入室总压。假设吸入室静压为极限真空压力，吸入室总压为引射蒸汽入口压力。根据式(1)和式(2)即可求出极限真空压力px。

混合室内流体为超音速流动，根据式(1)、式(2)和图10，马赫数大于1时，At/Am及px/p*随Mm的增大而减小，因此保持At和p*不变，增大Am，则Mm随之增大，从而px下降。

图10 不同比值随马赫数的变化曲线

如图11所示，二次喉道直径在原等截面引射器的基础上保持不变，设混合室收缩角为5°，通过增加混合室直径Dm，将原等截面引射器调整为二次喉道引射器，混合室直径在1.104 m的基础上依次增加0.05，0.1，0.2，0.3，0.4 m，引射器长度为Lm。

图11 二次喉道引射器示意图

表5为不同混合室直径的计算结果，从表5中可以看出，随着混合室直径增大，真空压力减小。当直径增加0.3 m时，真空压力较变化前下降39.92%。从图12的马赫数分布中可以看出，随着混合室直径增大，在保持混合室收缩角不变的前提下，引射器长度增加，二次喉道内的马赫数越来越小，当马赫数接近于1时喉道会发生壅塞，导致引射器不启动。

表5 不同混合室直径下的数值模拟计算结果

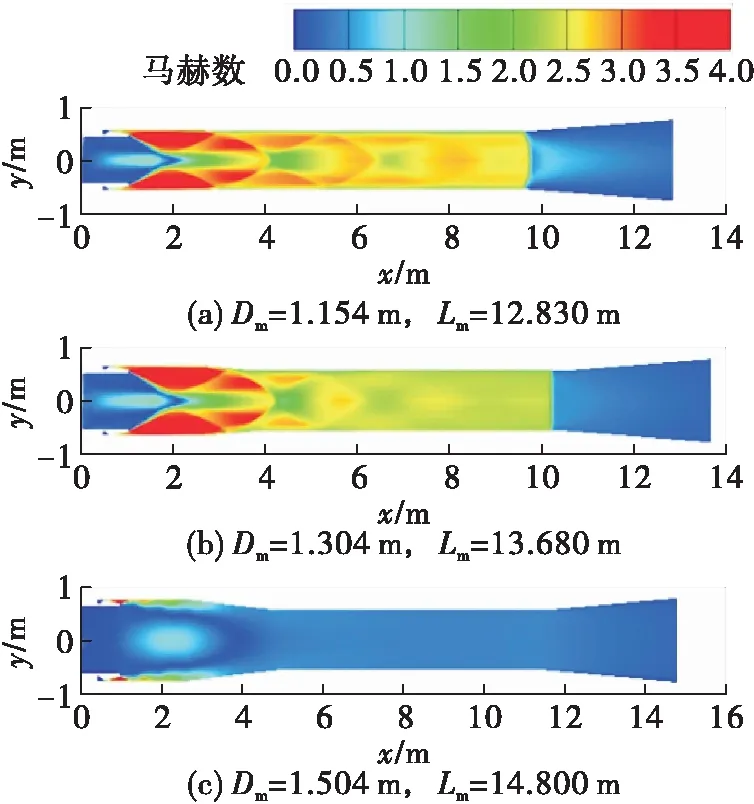
图12 不同混合室直径下的马赫数分布

3 结论

1) 建立了环形蒸汽引射器数值仿真模型，通过Fluent对引射器内部流场进行分析，并对比试验数据，验证了考虑水蒸气相变模型的仿真结果的准确性。

2) 入口工况对引射器性能有影响。若保持蒸汽入口总温不变，只改变入口总压，真空压力随入口总压的升高而升高；若保持蒸汽入口流量不变，改变入口总温，真空压力随入口总温的升高而降低。因此，在保证引射器正常启动的前提下，降低引射蒸汽入口总压，升高入口总温，可以降低真空压力。

3) 环形引射器喷嘴出口壁厚和混合室直径对真空压力有影响。在入口工况不变的前提下，减小喷嘴出口壁厚或增大混合室直径，真空压力降低，但是混合室直径过大时引射器可能不启动。