双向对冲流灌水器模拟精度综合评价指标

郭霖，白丹，王新端，王程，周文，程鹏

(1. 西安理工大学水利水电学院，陕西 西安 710048； 2. 西安浐灞生态区管理委员会，陕西 西安 710024； 3. 华北水利水电大学水利学院，河南 郑州 450011)

灌水器的结构设计与性能分析通常采用试验测试[1-3]、Fluent数值模拟[4-5]以及PIV流场观测[6]等方法，但对于流道尺寸狭小、边界复杂的灌水器而言，常规试验难以测试灌水器流道的流场特性和消能机理.因此，Fluent数值模拟方法被国内外许多学者广泛运用于灌水器的研究当中.

目前普遍采用Fluent数值模拟方法计算不同压力和不同流道结构参数的滴灌灌水器的流量、速度场、压力场和涡度场[7-9]，以分析灌水器流动机理[10]和水力性能[11-12]，从而缩短研发周期，弥补试验测试的一些不足.但由于模拟软件中许多因素的选择对数值模拟结果影响较大，尤其是物理模型和壁面函数对模拟结果的影响最为突出，合理地选择物理模型与壁面函数，并评价数值模拟的计算值与实测值的吻合程度，以提高数值模拟计算的精度，是开展滴灌灌水器数值模拟的关键.

通常用来评价滴灌灌水器数值模拟精度的指标可分为2个：一是宏观评价指标，即比较流道流量模拟值和实测值偏差；二是微观评价指标，即比较流道流场空间各点的流速模拟值和实测值偏差.由于2个评价指标均存在一定的片面性，因此，文中综合考虑宏观和微观2个方面，以常规灌水器类型双向对冲流灌水器为研究对象，着重对壁面函数处理和物理模型进行对比分析，建立合理的滴灌灌水器数值模拟精度评价指标.通过2个评价指标不同权重系数的综合评价，拟对灌水器数值模拟精度与适用性分析提供方法和思路.

1 灌水器流道结构及试验

1.1 灌水器流道结构

双向对冲流灌水器流道结构如图1所示，其中流道的核心部件为分水件和挡水件.

图1 灌水器结构图

1.2 灌水器流道几何参数

流道单元关键几何参数取值参照文献[13]，流道单元几何参数如图2所示，图中S为分水件与边壁的间距，T为挡水件齿尖与分水件的间距，W为挡水件与边壁的间距，Z为挡水件与分水件最大过水通道宽度，d为挡水件底柱高.

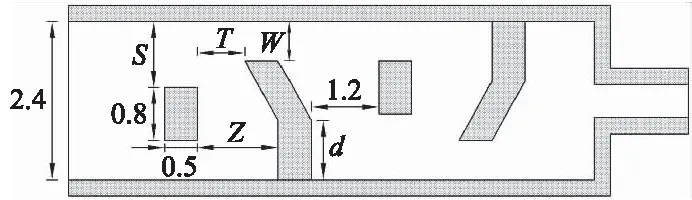
图2 灌水器流道单元几何参数图(单位：mm)

设计3种不同几何参数尺寸的灌水器流道样机，样机1和2作为对比组，样机3为实例验证组，其灌水器样机尺寸如表1所示.

表1 灌水器样机

1.3 灌水器试验装置

灌水器试验系统布置与测试方法参照GB/T17187—2009的要求设计，试验装置布置与PIV系统如图3所示，灌水器的工作压力通过水泵的转速以及进口压力表前端的控制阀进行调节.

图3 试验装置与PIV系统图

1.4 灌水器流量测试

灌水器在不同工作压力下流量与压力的关系可表示为

q=kHx，

(1)

式中：q为灌水器流量，L/h；k为流量系数；H为入口压力，kPa；x为流态指数.

为了提高流量测试的准确性，每种灌水器样机安装5个试件进行测试，每个工作压力测试3次，每次测试时间均持续5 min，并取3次测试的平均值作为灌水器的试验流量.工作压力在50～250 kPa范围内灌水器样机1和2测得的流态指数分别为0.432和0.464，其流量值如表2所示.

表2 流量测试结果

1.5 灌水器流速测试

图4为随水流方向从灌水器流道的进口到出口取不同位置的速度点，并采用PIV测试不同压力下各个点的速度.为了提高PIV流速测试结果的可靠性，其测试方法与流量测试相同，样机1和2的速度v1,v2测试结果如表3所示.

图4 不同速度点位置

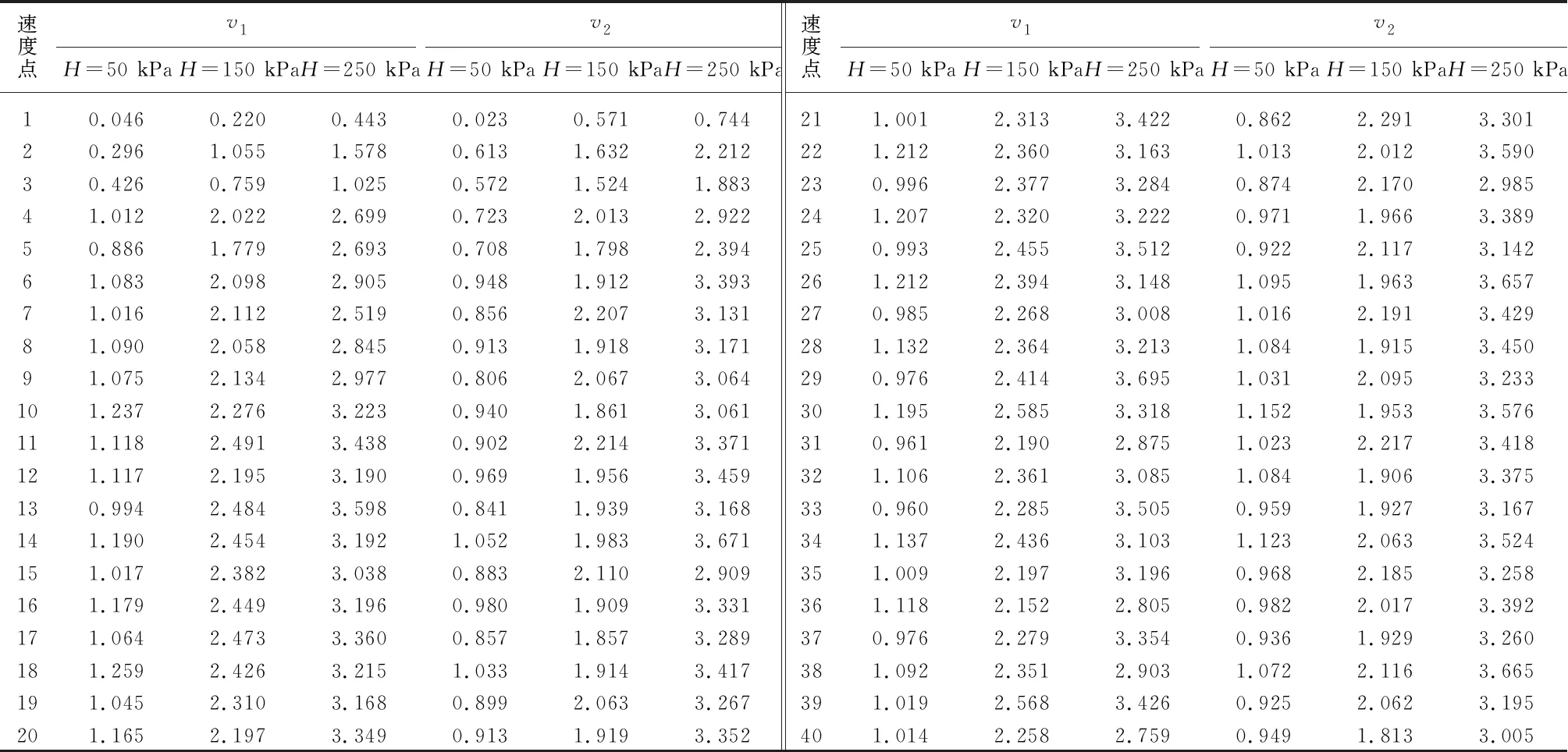
表3 流体速度测试结果

2 影响Fluent数值模拟精度的因素

2.1 数值模拟基本方法设置

为保证模拟精度，流道网格单元都将0.1 mm的非结构化四面体混合型网格作为单元尺寸划分网格；在Fluent求解器中，流道边界条件在Define选项的Boundary conditions中设置，流道边壁默认为边壁WALL；为了提高模拟精度，在Solve选项的Solution controls中设置二阶迎风格式(second order upwind)，同时为使迭代计算降低误差，在Residual monitors中设置计算残差为10-5，比标准残差值提高了1个数量级；为增强计算的稳定性，速度和压力耦合采用精度较高的Simple算法处理.

2.2 壁面函数

由于各种物理模型都是针对内部充分发展的湍流有效，而在近壁区由于分子黏性的影响大于湍流脉动，湍流发展并不充分，因此，需要在流道近壁区域采用不同的壁面函数进行处理.尤其对k-ε系列模型而言，不同壁面函数处理对其计算精度的影响很明显，因此分别对标准壁面函数、非平衡壁面函数以及增强壁面进行精度分析.

2.3 物理模型和模拟方法组合方案

Fluent软件的物理模型可分为k-ε，S-A，k-ω，RSM 4种系列7类模型.根据不同壁面函数和物理模型的计算适用性，对3种壁面函数和7类物理模型进行全面组合，同时由于S-A模型、标准k-ω模型、SSTk-ω模型只能采用增强壁面函数计算，因此可组成15种模拟组合方案，如表4所示.

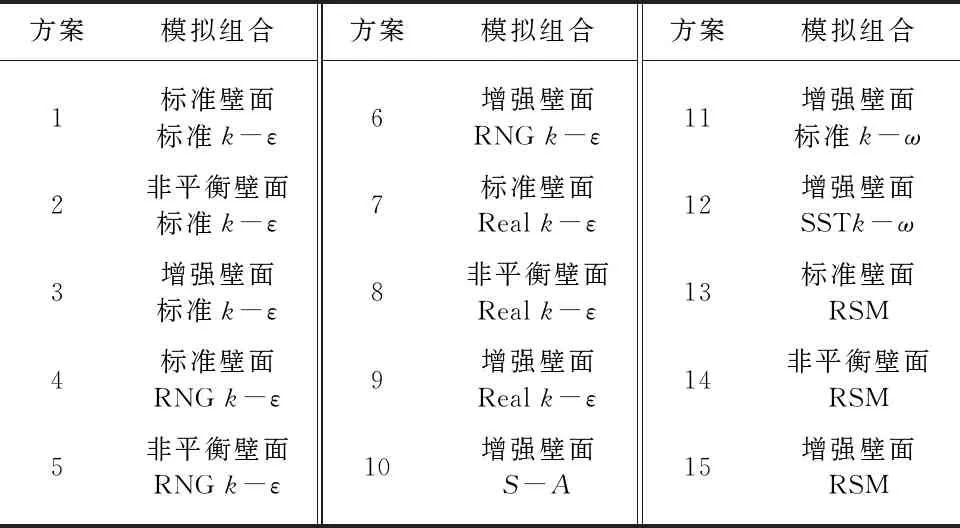
表4 数值模拟组合方案

3 综合评价指标的建立与分析

宏观评价指标和微观评价指标分别代表了灌水器流量和流速的计算值与实测值之间的吻合程度，各评价指标值用灌水器流量和流速的模拟值与实测值的偏差率表示，其中偏差率以5%为模拟精度优劣的评判依据，指标值(偏差率)越小，说明数值模拟组合方案的模拟精度越高.由于2个评价指标均有一定局限性，因此，综合考虑宏观和微观2个方面，并建立综合评价指标模型.

3.1 宏观评价指标

根据表4中列出的15种方案对灌水器进行流量模拟，并与实测值比较，对比结果如表5所示，表中β1为宏观指标值.

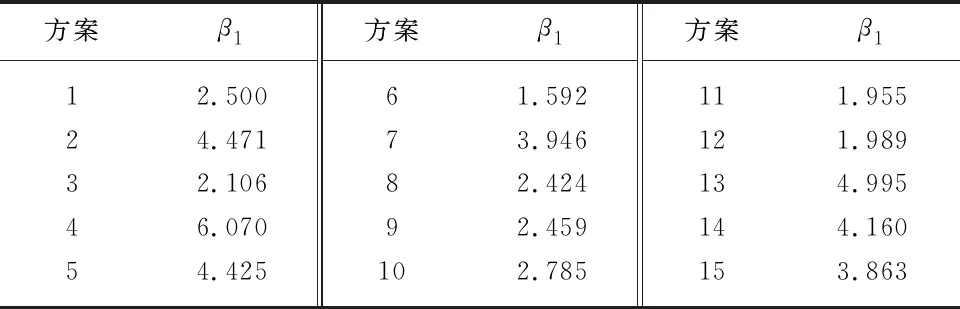
表5 宏观评价指标结果

对比15组方案流量的偏差率不难发现，宏观评价指标中模拟组合方案6的指标值(偏差率)最小，为1.592%.而偏差率较大的模拟方案中标准壁面函数和非平衡壁面函数所占的比例很大，这与其更加适合解决高雷诺数流动问题有关，而增强壁面函数更适合于解决低雷诺数和复杂近壁面现象的流动问题，其解决的流动问题更接近于灌水器流道的真实流动现象；RSM模型为高雷诺数的七方程湍流模型，从偏差计算结果可以看出，RSM模型的计算精度偏低，这种高雷诺数、强旋流模型并不适合灌水器流道的模拟计算.这是由于虽然RSM模型更加严格和精细地考虑了各向异性复杂流动，避免各向同性的涡黏性假设，增加了模拟旋转流动和表面曲率变化的影响方程，但其更适用于强旋涡流等复杂三维流动，同时由于模型方程的复杂性，需要占用更多的计算机资源、花费更多的计算时间，因此计算精度受到很大的影响.

3.2 微观评价指标

由于工作压力范围较大，数值模拟组合方案和测试数量较多，篇幅有限，仅对宏观指标中精度较高的4组模拟方案，即方案3,6,11,12绘制1个压力工况下的流体速度曲线图，其他模拟方案和不同压力下的微观评价指标结果以列表的形式逐一列出.图5以工作压力范围内的中间值150 kPa为例，绘制不同位置点流体速度图，观察流速的变化趋势.

在150 kPa工作压力下流道内流体速度基本保持在1.8～2.4 m/s，且随位置点的变化呈上下波动趋势，各点流体速度的模拟值与实测值基本吻合.

为了更直观地对比15种模拟组合方案流速模拟值与实测值的偏差率，列出对比结果如表6所示，表中β2为微观指标值.

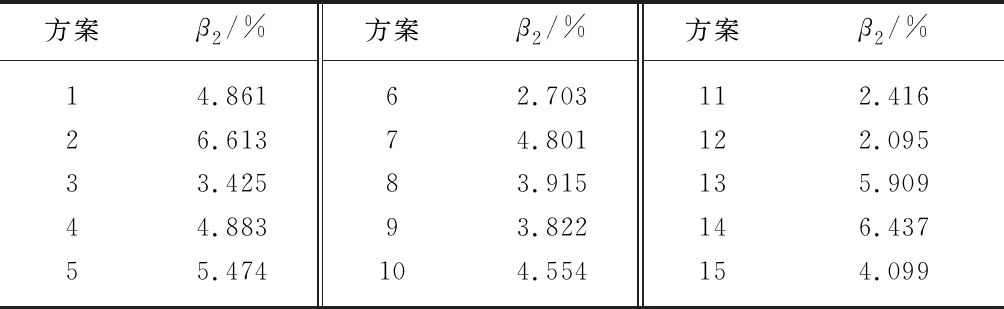
表6 微观评价指标结果

从结果可以看出，模拟组合方案12流速的模拟值与实测值最接近，指标值(偏差率)为2.095%；而宏观指标中精度最高的方案6的微观指标值(偏差率)为2.703 %.由此可见，2种评价指标分析数值模拟精度时所得到的结果有时并不一致，需要建立综合评价指标模型对2个评价指标进行综合评价.

3.3 综合评价指标

3.3.1 综合评价模型建立

一般多指标综合评价可通过一定的数学模型将多个评价指标合为一个整体的综合评价值[13].文中采用线性加权型评价模型对各评价指标进行计算.

线性加权型评价模型可表示为

(2)

式中：y为评价模型的综合评价指标值，%；wi为权重系数；βi为各评价系统的评价指标值，%.

3.3.2 权重系数计算

在多个评价指标中引入权重系数可协调和平衡各指标之间的区别，反映不同指标的重要程度.文中采用变异系数法计算权重系数.

各项指标的权重系数为

(3)

(4)

式中：Cvi为评价指标值的变异系数；σi为评价指标值的标准差，%.

计算可知，宏观评价指标的权重系数为0.6，微观评价指标的权重系数为0.4.

3.4 综合评价分析

根据综合评价模型对不同数值模拟组合方案的2个评价指标值进行综合对比，计算结果如表7所示.

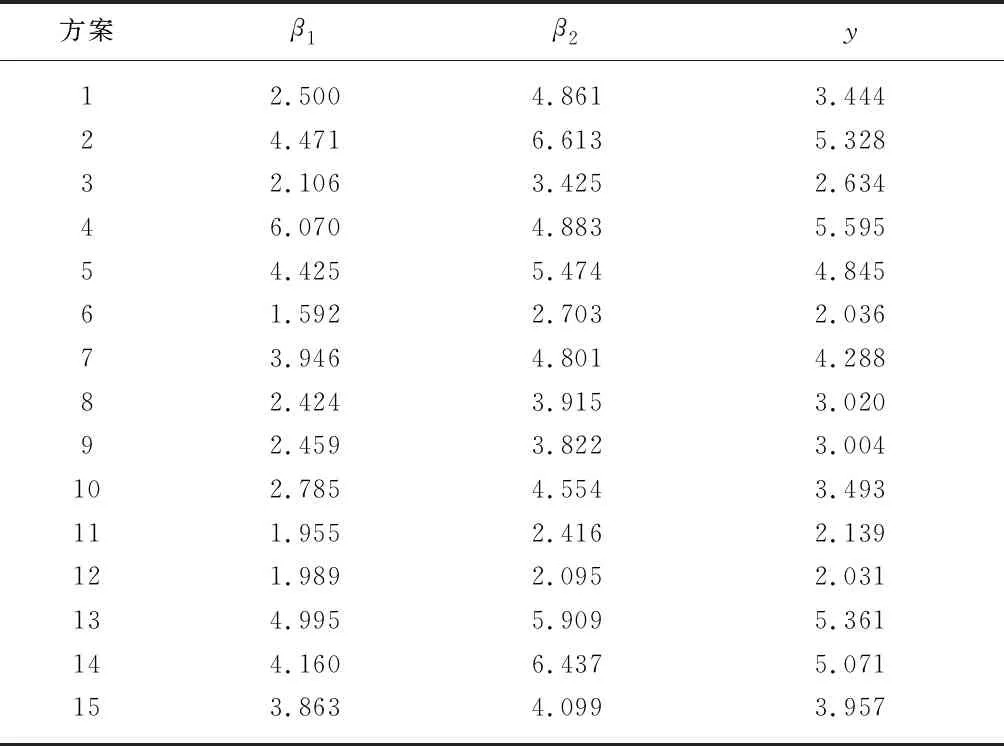
表7 综合评价指标结果

采用宏观评价指标计算得到流量模拟值与实测值偏差率最小的方案为数值模拟组合方案6，而采用微观评价指标计算得到流速模拟值与实测值偏差率最小的方案为数值模拟组合方案12.由于2个评价指标所得到的结果有所差异，因此，应对每个数值模拟组合方案的宏观评价指标和微观评价指标分别赋予权重系数0.6和0.4，计算得到数值模拟组合方案12的综合评价指标值最小，为2.031%.该模拟组合方案对于双向对冲流灌水器在宏观流量计算和微观流速分析方面更加精确和合理.

4 实例验证

对综合评价结果的准确性做进一步验证，以灌水器样机3为验证样本，采用模拟组合方案12计算的结果表明，验证样机3的宏观评价指标为0.923%，微观评价指标为1.883%.根据宏观评价指标的权重系数为0.6，微观评价指标的权重系数为0.4，计算得到样机3的综合评价指标为1.307%，小于5%的偏差标准，证明了采用综合评价指标方法计算的准确性和可靠性.

数值模拟组合方案12的流量和150 kPa工作压力下的流速曲线如图6，7所示.

图6 样机3的流量-压力曲线图

图7 样机3的流体速度图

5 结 论

1) 以新型双向对冲流灌水器为研究对象，共安排15种数值模拟组合方案，对15种方案进行精度对比.以流量偏差率作为宏观评价指标，得到模拟方案2，4，5，13的偏离程度较为明显，其中模拟方案4的偏差率最大，宏观评价指标值为6.070%；模拟方案3，6，11，12的偏离程度较小，其中模拟方案6的偏差率最小，宏观评价指标值为1.592%.

2) 以流速偏差率作为微观评价指标，当工作压力在150 kPa下不同位置点的速度基本保持在1.8～2.4 m/s、分析得出不同工作压力下模拟组合方案2流速的模拟值与实测值的偏差率最大，其微观评价指标值为6.613%；模拟组合方案12流速的模拟值与实测值最为接近，微观评价指标值为2.095%.

3) 采用线性加权法建立综合评价模型，并采用变异系数法计算出2个评价指标的权重系数分别为0.6和0.4，综合对比模拟组合方案12的综合评价指标值为2.031%，能准确模拟灌水器流量和流速.

4) 对综合评价结果的准确性做进一步验证，采用模拟组合方案12对验证样机进行计算，得到的宏观评价指标为0.923%，微观评价指标为1.883%，综合评价指标值为1.307%，偏差率小于5%，证明了采用综合评价指标方法计算的准确性和全面性.