考虑投资者情绪的中国股市自激发效应研究
唐振鹏,吴俊传,冉 梦,张婷婷
(福州大学经济与管理学院,福建 福州 350108)
1 引言
股票市场的风险管理一直是各国金融监管当局、各类投资主体迫切关注的焦点。自上世纪90年代以来,金融市场上出现了一系列金融灾害事件,如,1997年亚洲金融危机,2008年全球金融危机,2009年爆发的欧洲债务危机、迪拜危机,2015年中国股灾事件等。这些金融灾害性事件使全球经济发展遭受了重大创伤,也进一步警示我们:一国的经济发展和金融稳定离不开强有力的金融市场风险管控。长期以来,基于理性人假设前提建立的有效市场假说(Efficient Market Hypothesis,EMH)一直是现代金融市场理论的基石。该假说认为金融市场上资产价格收益率序列服从正态分布(Normal Distribution),然而,大量学者发现金融资产收益率序列数据具有尖峰厚尾特性,当面临极端事件的冲击时,金融资产价格短期内连续暴涨、暴跌现象时有发生,若仍然假定金融资产价格服从正态分布,将会造成风险的严重低估。
自20世纪80年代中期以来,金融市场上涌现出大量异常现象,如股价动量效应、长期反转效应、处置效应、股权溢价之谜、心理账户等。行为金融学(Behavioral Finance)以市场参与主体非理性假设为基础,将心理学、行为科学的研究成果融入到传统金融学理论中,能有效解释这类普遍存在的异象。作为行为金融学的重要分支,投资者情绪(Investor Sentiment)迅速成为金融、经济学领域的研究热点。国内外大量学者研究投资者情绪对证券市场资产收益率波动的影响,取得了一系列成果。Lee等[1]最早开展对投资者情绪的研究,他对投资者情绪与封闭式基金折扣率的波动关系进行了检验,发现投资者对封闭式基金未来回报的情绪变化确实可以有效地解释封闭式基金折扣率的波动。Fisher和Statman[2]发现不同市场参与主体的投资者情绪具有异质性,研究显示个人投资者的情绪与新闻撰稿人的情绪相关性较强,而华尔街策略分析师的情绪与前面两类投资者的情绪相关性较弱并且投资者的情绪与未来股市收益率负相关,对于华尔街策略分析师和个人投资者尤为明显。Persaud[3]运用外汇收益率与外汇风险的秩相关系数,设计风险偏好指数来反映短期内外汇市场上的投资者情绪,他认为短期内外汇市场上参与者的风险态度直接决定了外汇收益率的走势。Bandopadhyaya 和 Jones[4]依据Persaud[3]的风险偏好指数,选取242只彭博指数(MBI)指数成份股,计算其收益率排序与波动率排序的斯皮尔曼秩相关系数,构建了股票市场情绪指数(Equity Market Sentiment Index,EMSI)用于反映股票市场上的投资者情绪。对MBI指数收益率作回归分析,发现 EMSI 指数和滞后一期的MBI指数对MBI 指数的收益率具有较好的解释能力(其调整的可决系数达到0.56)。Huang Dashan等[5]从6个情绪代理指标中提取相关性最强的共同成份,构建一致投资者情绪指数,实证结果表明该情绪指数能较好地预测股市的走势。Wang Qili等[6]将公众情绪与技术分析相结合,提出一种融合深度学习算法和集成学习方法的机器学习技术—深度随机子空间集成(Deep Random Subspace Ensembles, DRSE)来预测股市收益率,取得了较好的预测效果。国内学者方面,李合龙和冯春娥[7]采用集成经验模态分解(EEMD)方法分别提取投资者情绪及股指价格序列不同时间尺度下的波动特征,实证结果表明短期内,投资者情绪与股指收益率波动相互影响,而中期股指收益率波动滞后于投资者情绪的波动。陈其安和雷小燕[8]发现投资者情绪和中国股票市场价格波动呈正相关关系,并发现投资者情绪一定程度上削弱了货币政策调控股市的效果。许启发等[9]等采用分位数格兰杰因果检验方法,检验网络情绪与沪深300指数收益之间的因果关系,实证结果表明投资者情绪与极端收益关联性较高,对股市收益率序列尾部产生了Granger因果影响。纵观现有研究,多数学者构建的投资者情绪指数均为周度或月度频率指数。当前,也仅有少部分学者采用数据挖掘、文本分析等方法提取日度情绪指数,而受制于前期互联网技术的发展,这一类方法只能获取最近时段的投资者情绪,无法完整刻画股市不同时期的投资者情绪,限制了模型的分析,而EMSI情绪指数通过简单的统计方法便能度量股市每一个时期投资者情绪,更适合与其它模型相结合进行分析。
为了更好的刻画金融资产收益率序列分布的尖峰厚尾特性,大量学者[10-11]提出采用基于超阈值模型(Peaks over threshold, POT)中的广义帕累托分布(Generalized Pareto Distribution, GPD)来拟合金融资产收益率序列的尾部数据,以便捕捉金融市场在极端情形下的风险。GPD分布假设极端值数据服从独立同分布,即极端值事件之间互相独立,极值在不同时刻出现的概率相同,极值序列遵循齐次泊松过程。然而在现实的金融市场中,极值事件经常集聚出现并伴有短期相依性,因此自激发点过程(Self-Exciting Point Process, SEPP)恰好可以用来描述金融市场中稀疏极值事件所呈现的这两种特性。自激发点过程最早由Hawkes[12-13]提出,它可以用来描述随机点过程中随机点事件集聚发生这一特性和点事件之间的短期相依关系。Chavez-Demoulin等[14]将极值数据超出某一特定的阈值后的超出量作为标值,并结合霍克斯自激点过程构造出标值自激发点过程(Marked Self-Exciting Point Process, MSEPP),同时运用该方法对拜耳股票指数、道琼斯指数及美元对马克外汇指数进行VaR测度取得了较好的效果。Herrera[15]在POT模型的基础上引入标值自激点过程对美国西德克萨斯轻质原油、布伦特原油市场进行动态VaR测度,实证结果表明,标值点过程的引入改善了传统GPD分布的VaR测度效果。Gresnigt等[16]在传统的GPD分布中引入霍克斯标值自激点过程来预测2008年金融危机期间的标普500指数收益率发生崩盘的概率,发现该模型的效果优于传统的GARCH族波动模型。因此,在GPD分布中引入标值自激点过程理论探究中国金融市场风险测度的问题具有重要的研究价值。
目前, VaR (Value at Risk)方法是金融市场最常用的风险管理方法之一。然而众多研究表明,该方法存在一定缺陷[17-18]。此后,Artzner[17]提出了条件风险价值模型(Conditional risk value model, CVaR)。Rockafeller和Uryasev[19]提出了预期亏损(Expectd Shortfall, ES)模型。ES模型满足一致性风险测度条件,当CVaR模型经过适度修正之后便成为ES模型。自从ES测度方法诞生以后,大量学者进行了ES测度方法的研究。Harmantzis等[20]针对标普500指数、德国DAX综合指数、巴黎CAC40指数、TSE指数、FTSE指数、日经指数等指数收益率及美元对英镑、美元对欧元、美元对加元、美元对日元等外汇市场收益率分别采用GPD分布、正态分布、历史模拟法等度量其市场风险。研究发现,整体上,基于GPD分布的ES回测效果显著优于其它模型。Morgan等[21]采用GPD-VaR、GPD-ES方法度量美国大豆、玉米期货市场的极端风险,取得了优于N-VaR、N-ES方法的表现结果。Manel[22]等分别运用3种长记忆GARCH族模型——FIGARCH, HYGARCH 及FIAPARCH模型结合EVT度量原油和汽油市场的动态VaR、ES风险,取得了较好的表现。中国学者在这方面也开展了相关的研究。崔海蓉等[23]采用FIEGARCH-EVT-ES模型度量上海期货交易所铜期货的市场风险,结果发现FIEGARCH-EVT-ES模型预测效果优于GARCH-N-ES模型。陈倩[24]采用GPD-VaR、GPD-ES方法度量中国商业银行操作风险,取得了较好的效果。高岳和张翼[25]分别运用GARCH-GPD-VaR、GARCH-GPD-ES模型度量深圳成份指数市场风险,结果表明GPD分布取得了优于其它模型的效果。目前已有学者采用标值自激发点过程来进行VaR风险测度,但尚未有研究成果报道运用该模型进行ES风险测度。
综上,尚未有学者将标值自激发点过程应用于股市动态ES风险测度,也未有学者将投资者情绪纳入到标值自激发点过程当中,探讨投资者情绪对股指极端风险的影响。本文采用标值自激点过程来刻画股指收益率极端损失序列的集聚性、短期相依性,以弥补传统POT模型的不足。利用沪深300指数成份股构建中国股市投资者情绪指数,并将该指数纳入标值自激点过程,以反映投资者情绪对极端损失的冲击。最后构建MSEPP-EMSI模型对沪深300指数、上证指数、深证成份指数进行样本外极端风险概率预测及动态ES测度。本文的贡献主要体现在:(1)采用标值自激发点过程刻画股指收益率极端值序列的集聚性、短期相依性,并对其进行风险概率预测及ES测度;(2)考虑投资者情绪对股市极端风险的冲击,构建MSEPP-EMSI模型对股指收益率进行风险概率预测及ES回测,改善风险测度效果。本文的研究揭示了中国股市极端风险的自激发效应,并且负面投资者情绪会加剧这一效应,有助于解释股市中广泛存在的连续暴跌现象。同时可在股市出现连续极端风险的情况下指导投资者的交易行为、增强机构投资者在面临连续极端风险状况下的风险管理水平,并为政府监管部门制定政策提供依据。
2 模型介绍
2.1 MSEPP-EMSI模型设计原理
2.1.1 投资者情绪指数的构建
Persaud[3]在外汇收益率与风险的秩相关系数的基础上设计风险偏好指数(Risk Appetite Index)来测量投资者情绪。市场风险偏好指数越高,表明投资者情绪更加乐观;市场风险偏好指数越低,表明投资者情绪更加悲观。他认为短期内,外汇市场参与主体对风险偏好的改变是导致外汇收益率发生变动的重要驱动因素。当市场收益率的变化方向与投资者的风险承受水平的变化方向一致,表明投资者愿意承担高风险来换取高额收益,市场整体的风险偏好较高,投资者情绪偏乐观,反之则偏悲观。Bandopadhyaya 和Jones[4]依据上述方法,选取来自美国马萨诸塞州彭博指数中242只成份股,构建了Equity Market Sentiment Index(EMSI)指数用于反映股票市场上的投资者情绪。
参照EMSI指数的设计原理,本文基于沪深300指数所有成份股来合成中国EMSI指数,
其表达式为:
(1)
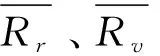
2.1.2 广义帕累托分布(GPD)
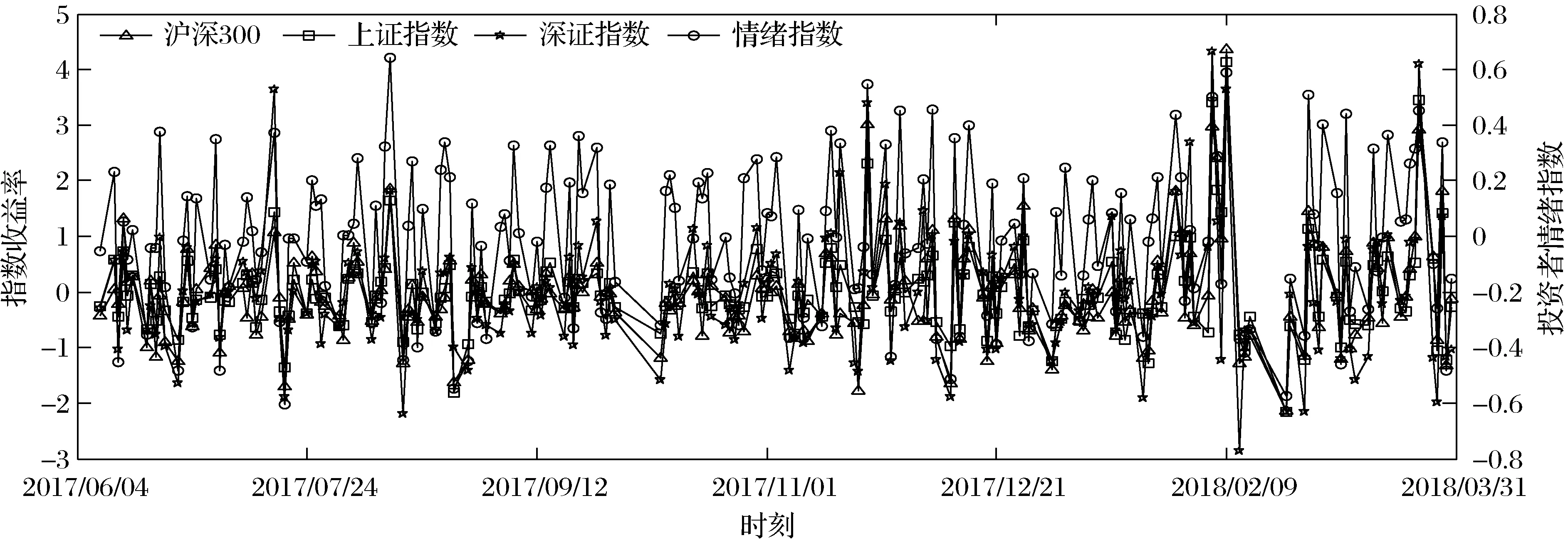
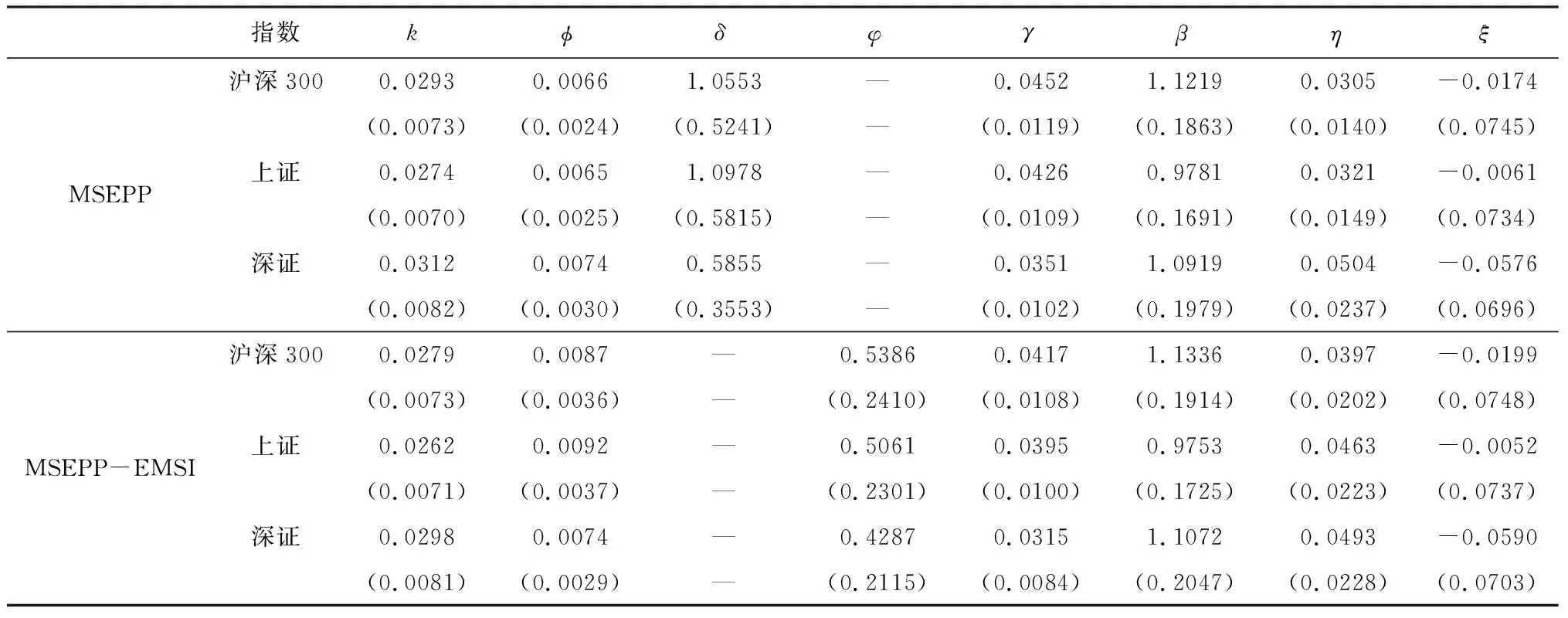
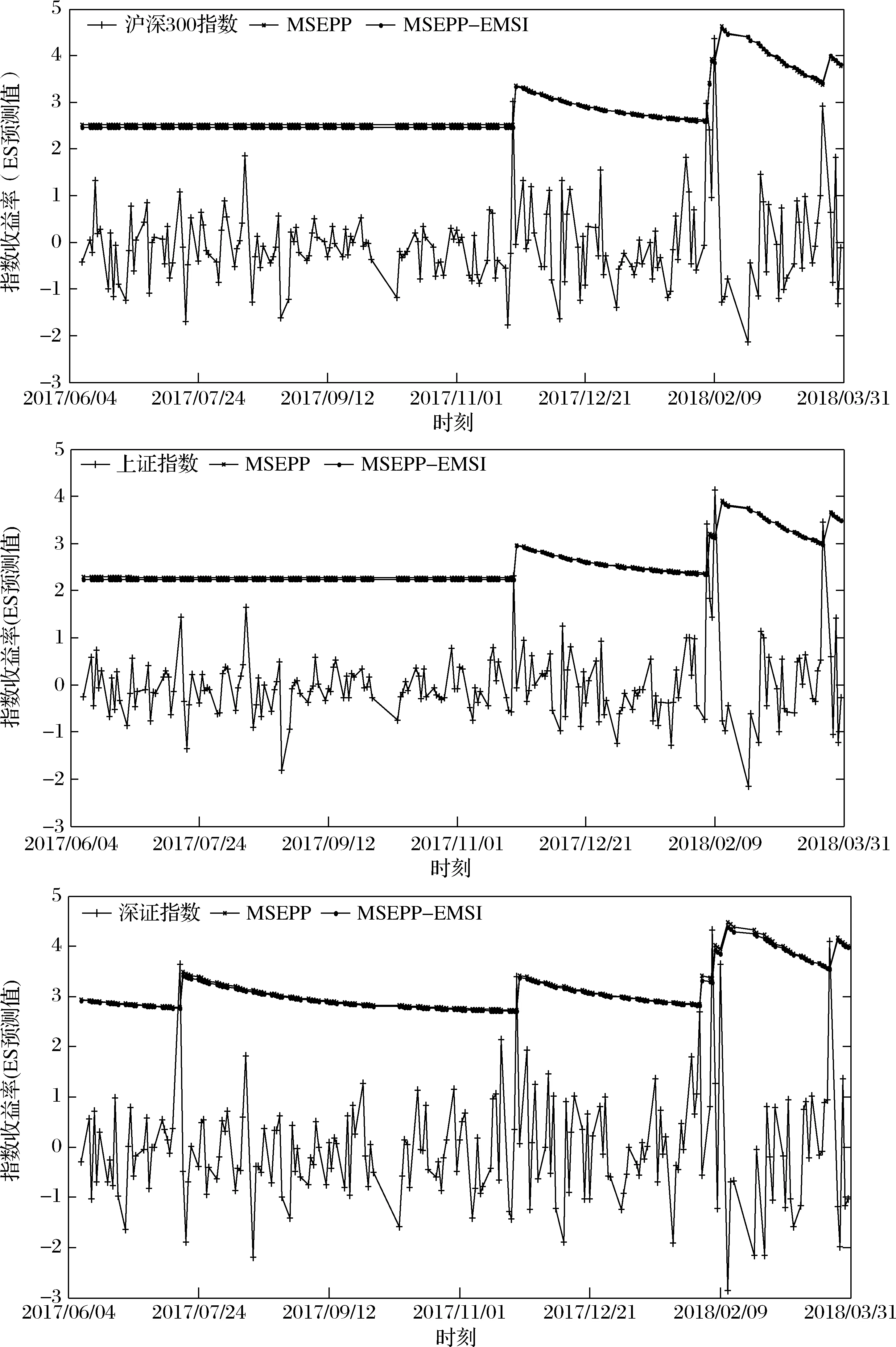
设有来自同一总体分布函数FX(x)的随机变量X1,X2,…,Xk,该总体分布支撑的上端点为x*,选取阈值u(u (2) 当ξ≥0时,y∈[0,∞);当ξ<0时,y∈[0,-σ/ξ]。式中ξ为形状参数(Shape Parameter),σ为尺度参数(Scale Parameter)。以ξ≠0时的情形为例,其极大 似然估计为[10]: L(ξ,σ|y))=-nlnσ (3) 当考虑由特定时间段内发生的极值事件所构成的泊松过程的强度函数时,由于极值事件的发生强度独立于标值,其极大似然估计变为[15]: (4) 式中,gξ,σ为广义帕累托分布的密度函数,并且该式又可以表示为L(ξ,σ,λ|y))=LNu(λ)+L(ξ,σ|y)),因此,我们可以将总体分为强度函数部分与标值部分分开来进行估计。对比(3)与(4),我们发现,传统的POT模型即为假定特定时间段内发生的极值事件数目所形成的泊松过程的强度为常数时的特例。 2.1.3 标值自激发点过程(MSEPP) 2.1.2中假设极值数据服从独立同分布,然而这显然与实际情况不符,现实金融市场中,若干个极端风险事件很可能会相继发生,并且极端风险事件之间存在相依性。为了更有效地刻画这一特性,本节将在POT模型中引入标值自激点过程来做分析。 设存在点过程事件(Ti,Yi),i=1,…,n,n为点过程中事件的样本容量,Ti为某点过程事件出现的时间,本文中即为极值数据出现的时刻,Yi=Xi-u为标值,即极值数据Xi超出阈值u以上的超出量。进一步假定有来自[0,T]时间段内的点数据(T1,Y1),…,(TNu,YNu),Nu意义同2.1.2。由(T1,Y1),…,(TNu,YNu)所表示的复合点过程的强度函数为λ(t,y)。本节中,λ已不再为常数,而是随着时间的变化而发生改变。 Hawkes 过程具有典型的自激发(Self-Exciting)特性, 按照该过程的定义,极值的出现遵循某一基准强度,极值事件一旦出现,基准强度便向上跳跃,进一步激发后续极值事件的出现。按照霍克斯[12-13]的定义,过去发生的极值事件决定了当前极值事件发生的强度。Herrera[15]通过引入霍克斯(Hawkes)自激发点过程来描述λ及f(y)中尺度参数β(t,y)的变化。其具体形式有: λ(t,y)=k+φ∑i:ti (5) (6) 由(5)、(6)式得,Herrera认为该二维点过程的条件强度不仅受各标值出现时刻的影响,同时还受标值本身的影响。k、β0不随时间的改变而改变,也称作极值出现的基准强度。(5)、(6)式中的叠加求和反映了自激发效应。φ,η≥0,反映了前期已出现的极值所带来的激发强度。g(·)为前期已出现极值事件的出现密度。本文采用霍克斯核密度函数(Hawkes Kernel Density Function)[15]来描述极值事件的出现密度。其具体表达式为: g(t-ti,yti)=(1+δyti)e-γ(t-ti) (7) 因此,将(7)式代入到(5),(6)式可得: (8) (9) 式中,t-ti表示第i个极值事件发生的时刻ti距离当前时刻t的时间间隔。γ表示前面已发生的极值事件影响力的衰减力度,γ越大,前期发生的极值事件对当前事件的影响力就越小,当前事件的发生频率就会降低,反之亦然。δ代表了已发生的极值事件的标值yti对当前极值事件的影响,δ>0,表明已发生的极值事件会提高当前极值事件发生的频率。 f(y)中的形状参数ξ亦可表示为时变形式,然而当ξ为时变时,会造成参数估计的困难,因此仍然假定ξ的值为一个常数,该复合泊松过程总体对数似然函数为[15-16]: (2) 受雨水入渗的作用,最先在坡脚部分出现塑性破坏,然后塑性区域由坡脚逐渐向坡顶延伸,最后塑性区域贯通并扩大,造成边坡破坏失稳。 (10) 式中,P(ti)为极值在ti时刻到达的条件概率密度函数。从上式得,可以将其总体对数似然函数表示为标值出现的时刻的对数似然函数加上标值本身的对数似然函数。 2.1.4 MSEPP-EMSI模型构建 2.1.3介绍的MSEPP中,并未考虑投资者情绪对极端损失的冲击,而现有的研究[4-9]表明投资者情绪会显著影响股市收益率。为了刻画投资者情绪对极端损失的影响,在MSEPP模型中纳入投资者情绪对极端损失的冲击,其强度函数和尺度函数可进一步表示为: (11) (12) 式中,mti为损失极端值标值yti对应的情绪值,φ为投资者情绪对极端收益的冲击,φ>0,则表明投资者情绪会对极端收益形成正面冲击,反之亦然。设已发生的极值事件的标值为yti,若其对应的情绪值mti偏悲观,该悲观情绪会助推标值yti对当前极值事件的影响,该负面情绪会进一步加剧市场悲观预期,导致接下来市场爆发极端风险的频率进一步增加;反之,若极端风险对应的情绪出现反转,市场情绪转变为乐观情绪,该乐观情绪就会抑制已发生的极值事件对当前事件的冲击,则接下来市场爆发极端风险的频率就会降低。 2.2.1 极端风险概率预测原理 股市投资者、投资机构风险经理以及金融市场监管部门等均可受益于对股市崩盘风险的概率预测。由带时倚强度λt的泊松过程的定义可知[26],在t至t+s时间段内,事件发生的概率由下式给出: P(Nt+s-Nt>0)=1-P(Nt+s-Nt=0) =1-exp{-[Λ(t+s)-Λ(t)]} (13) 本文采用Gresnigt等[16]提出的QPS、LPS统计量来评估模型的预测效果。 (14) (15) 2.3.1 ES风险测度原理 由VaR的定义可知,VaR实质上为金融资产价格对应分布函数在某一置信度水平下的分位数。设有来自分布函数为F(x)的金融资产价格序列X1,X2,…,Xn,其对应q置信度水平下的VaR表达式为F-1(q)。因此,取(2)式的逆函数,便得到GPD分布下的VaR测度的表达式: (16) (17) 设初始阈值为u0,由GPD分布的性质可知[27],当取更大的阈值u′,收益率样本超出阈值u′以上的超出额亦能用GPD分布来拟合,并且2者的ξ、σ取值相同,其平均超额函数为: (18) 针对VaR风险度量方法的缺陷,Rockafeller和Uryasev[19]给出了预期亏损模型ES。按照其定义, ES衡量当金融市场爆发极端风险,即实际的损失超过对应置信度水平下的VaR值时的条件期望。给定置信度水平q,第t天ES值为未来的收益率序列超过VaR值的条件数学期望,其数学表达式为: (19) E(rt-VaRt|rt>VaRt)) (20) 进一步,可得MSEPP、MSEPP-EMSI模型的动态ES测度公式: (21) ξ为MSEPP、MSEPP-EMSI模型下的形状参数,u同POT模型中的阈值。 2.3.2 ES回测原理 (22) (23) (24) VES的值越小,则模型ES回测检验效果越好。 为了使构建的情绪指数能刻画我国股票市场整体投资者情绪,本文选择沪深300指数作为建模对象。2005年4月5日,上海与深圳交易所联合发布了能够反映我国股票市场整体走势的沪深300指数。沪深300指数由A股市场规模大、流动性强的300只成份股组成,并且覆盖了市场6成左右的市值,具有较好的代表性。考虑到沪深300指数成分股名单不断调整,剔除部分编入指数时间较短、中间被调出指数的部分个股,最终以沪深300指数及285只成份股作为样本,构建反映我国投资者情绪的EMSI指数。选取沪深300指数及其285只成份股2005年4月5日至2018年3月30日数据作为分析对象,除去闭市期,交易天数总共为3009天。以100个交易日为滚动时间窗,最终得到2005年9月2日至2018年3月30日的EMSI指数序列。 采用沪深300指数、上证综合指数、深证成份指数作为样本数据,分析我国股市极端风险收益的自激发效应,与EMSI指数样本所属区间相对应,仍然选取上述3大指数2005年9月2日至2018年3月30日数据为分析对象,并选取区间内后300个交易日的数据作为样本外ES、条件概率预测后验分析。本文所有数据均通过Python财经数据接口包Tushare获得,Tushare包的数据来源为上交所、深交所、腾讯财经、新浪财经等。对收益率作对数化处理,定义第t天的收益率为rt=-100*[ln(pt)-ln(pt-1)],t=1,2,…,n,收益率为正值时代表损失,为负值时则代表盈利。同时,当情绪指数为正时,代表悲观情绪,反之,则为乐观情绪。 用于建模的样本数据的统计特性如表1所示,沪深300指数、上证综合指数、深圳成份指数的峰度 (Kurtosis) 系数分别为6.73603、7.39278、5.95789,超过正态分布时的3;所有指数的偏度(Skewness)系数均超过0,表明所有指数的分布均存在非对称效应。所有指数的J-B系数取值分别为1953.227、2668.212、1268.969,均大于卡方分布自由度为2时的临界值,即3大指数的分布均存在厚尾特性。综合来看,沪深市场收益率序列具有负偏、厚尾特性,并非服从正态分布。 表1 沪深股市收益率序列的统计特征 图1展示了2017年6月7日至2018年3月30日200个交易日的投资者情绪指数与对应的3大指数收益率的时序图。从图中可直观的看出,沪深300指数、上证指数、深证指数与EMSI情绪指数在波峰、波谷数值方面具有较强的同步性。即市场行情较差时,往往伴随着悲观情绪,行情较好时,往往伴随着乐观情绪。 图1 沪深300、上证指数、深证指数与EMSI情绪指数 GPD分布的拟合效果严格依赖于阈值u的选取,如果选取的阈值太低,则无法满足Pickands定理[29]的要求,拟合的GPD分布就不准确;阈值太高,虽然能够满足定理的要求,但是样本数据个数太少,会增大模型参数估计的方差,削弱其参数估计效果。DuMouchel[30]认为用于GPD拟合的超阈值数据不宜超过样本总体规模的10%;周孝华和陈九生[31]采用这一原则,选取总体样本的10%用于GPD模型的拟合,取得了较好的实证效果。本文也借鉴该方法来得到GPD估计的阈值。选取3大指数的90%分位点,得到其阈值分别为:2.0053、1.8914、2.1480。三大指数在不同情形下的参数估计结果如表2所示。 表2 不同指数标值自激发点过程估计结果 由2.2.1的分析可得,极值发生的时间可以看作是时间轴上的某个点。由非齐次泊松过程的相关知识可以得到某一时间间隔内,极端损失值产生的条件概率。将收益率序列数据、MSEPP及MSEPP-EMSI模型参数估计值代入公式(13),便得到各时刻产生极端损失值的条件概率。2015年夏季中国股市呈现剧烈异常波动,仅两个月时间内,上证指数从5178.19点高位滑落至2850.71点,期间资本市场上不断上演千股跌停的局面,其中绝大多数股票价格遭受无情“腰斩”,顿时恐慌情绪弥漫整个资本市场。图2展示了沪深300指数、上证指数、深证指数从2015年4月21日至2016年2月15日,中国股灾期间爆发极端损失的概率预测值。 从图中可直观看出,股灾期间,沪深300指数、上证指数、深证指数产生极端损失的概率相比其它时间段急剧上升。 表3报告了三大指数从2017年1月6日至2018年3月30日,共计300个交易日的样本外极端损失概率预测回测结果。从中可以看出,当考虑市场情绪对极端收益的冲击时,模型的预测效果得到改善,MSEPP-EMSI对三大指数的预测表现均优于MSEPP模型。 表3 三大指数极端风险概率预测回测结果 由2.3.1的分析可得到沪深指数收益率序列的动态ES预测值。图3报告了三大指数95%置信度水平下,样本外后200个交易日的动态ES预测值序列。 图3 沪深股市样本外200个交易日动态ES预测序列 由2.3.2的分析得,通过比较不同模型V值的大小便能衡量不同模型的ES预测的精度,V值越小的模型预测效果越好。2种模型样本外300个交易日的V值如表4所示,从中可以看出MSEPP-EMSI模型在绝大多数情况下取得最小V值,优于MSEPP模型的表现。 表4 沪深3大指数动态ES回测结果 本文借鉴风险偏好指数,利用沪深300指数成份股构建了中国股票市场投资者情绪指数(EMSI),发现投资者情绪指数与股指收益率序列存在显著的同步性。引入标值自激泊松点过程来刻画指数极端收益序列的短期相依性,将传统的POT模型所描述的齐次泊松过程拓展为带自激发效应的非齐次泊松过程。实证分析得出以下结论: 第一,极端值序列之间存在明显的短期相依关系,传统极值理论中极端值之间相互独立的假设明显与事实不符。2008年金融危机及2015年股灾期间,股指价格发生剧烈波动,短期内连续暴涨、暴跌现象时有发生,极端损失值出现的概率剧增,并非如传统极值理论所假定的固定概率。 第二,投资者情绪对股指收益率存在显著的影响,极端负面情绪会加剧股指收益率暴跌,反之,极端正面情绪也会助推股指收益率暴涨。当遭受极端负面情绪的冲击时,接下来交易日股指出现暴跌的概率会增加,当遭受极端正面情绪的冲击时,接下来交易日股指出现暴跌的概率会被抑制。考虑投资者情绪的MSEPP-EMSI模型的QPS、LPS统计量均低于MSEPP模型,取得了较好的概率预测效果。 第三, MSEPP-EMSI模型能有效的刻画股指极端收益率序列的集聚性、短期自相关性等特性,并反映了极端负面投资者情绪对股指收益率的冲击,其动态ES回测表现在绝大多数情形下优于MSEPP模型。并且MSEPP-EMSI模型不需要借助于其它波动率模型便能实现动态VaR、ES测度,对金融资产收益率序列的风险测度更为直观。2.2 极端风险爆发概率预测
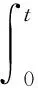
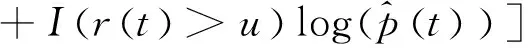
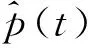
2.3 ES风险测度与回测检验
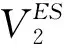
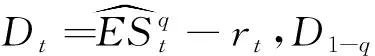
3 实证分析
3.1 数据来源与模型估计

3.2 极端风险概率预测结果分析
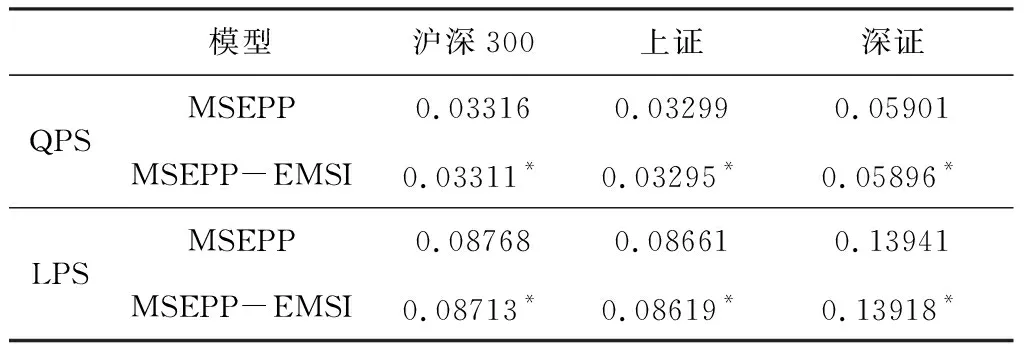
3.3 沪深股市动态ES回测结果

4 结语

