大型火车站候车厅腔体植入设计的舒适度关联研究*
夏柏树 张宁 白晓伟
沈阳建筑大学
大型火车站是典型的大空间建筑,候车厅具有突出的大空间特征,规模巨大,尺度超常,形态单一。相关文献研究表明,近年来我国新建的大型火车站,尤其是各中心城市的高铁车站,多采用穿越类线正上式布局,候车厅横向跨度50~60m,纵向跨度200~300m,基本采取集中、开敞的候车空间模式(图1)。对北方地区进行实地调研,我们发现大型火车站冬夏季普遍采用空调系统,能耗巨大[1],且体感舒适度不足;春秋季空调系统关闭,候车厅仅靠部分外窗、少量天窗和进站厅入口等进行直接或间接的换气,进出风量有限,候车厅获得的太阳辐射得热和室内人流散发的热量、CO2无法及时排出,造成室内空气质量下降,舒适度大大降低[2]。为此,在春秋季气候适宜的时段,在候车厅中植入腔体,建立新的自然通风路径,能够有效提高候车厅的舒适度。
广义上讲,在建筑内部能够起到调节物质、能量交换作用的空间都可视为腔体,具有生物体适应环境变化的通用特征[3,4]。常见的自然通风建筑腔体包括内置的庭院、室内的中庭和竖向的风井等多种类型。对大型火车站候车厅的自然通风而言,在当今通行空间单一和集中候车的模式下,选用竖向风井作为自然通风的腔体类型,既可以减少对候车厅功能布局的影响,也有利于在大空间内部形成均匀的自然通风,在实践中具有广泛的应用潜力。本文以风井类腔体为研究对象,探讨腔体的形态、布置和开口等设计参数对候车厅自然通风的影响,揭示腔体与舒适度之间的关联规律。
1 候车厅典型空间模型的建立
针对北方地区11个省市67个火车站的调研统计,大型火车站59座。其中,81%的大型火车站为穿越类线正上式布局,即候车厅位于站台上方;96%的火车站为工字形平面,即进站厅位于铁路两侧,以适应双侧进站的乘车要求;90%的火车站及候车厅平面形态为矩形,宜于满足功能流线要求;87%的候车厅侧界面被商业和附属空间遮挡,不开窗或很少开窗,有利于建筑保温;80%的候车厅屋面为平屋面,多设置采光天窗。基于以上调研统计分析,穿越类线正上式布局、工字形站房平面、矩形候车厅、平屋顶为北方地区大型火车站的典型空间形态。因此,在候车厅面宽、进深、高度方面,提取调研样本的平均值100m×240m×18m;在候车厅的进出风口方面,考虑到候车厅纵向外墙被商业附属用房遮挡,仅有的检票口在检票期间短暂开启,对候车厅通风作用有限,侧界面按封闭考虑;屋面天窗实际开启比例低,按无通风开口考虑;候车厅两侧进站厅各设10扇外门,每扇门尺寸为4.0m×3.6m,按常开状态考虑。基于以上分析数据,建立大型火车站候车厅的典型空间模型(图2)。
2 腔体植入模拟实验设计

1 穿越类线正上式空间模式

2 典型空间模型
选用CFD为模拟实验平台,通过前处理器Geometry建立参数化实验模型,调用Mesh建立全六面体网格,网格尺寸为1.5m,将网格传递到求解器Fluent中设置边界条件,包括围护体系的温度和传热系数、进风口的风速和温度、出风口的回流温度、室内人员的发热量和呼出CO2浓度等[5-8],输入腔体设计参数并赋值,进行迭代求解方程。当方程残差低于千分之一时默认收敛,即模拟结果最接近稳态。此时调用后处理器CFD Post进行处理,提取候车厅参考面舒适度指标,用来描述和判断候车厅自然通风效果。
2.1 模拟实验的自变量设置
以正方形截面、通高、顶部开口的腔体为模拟实验原型。先期通过对比实验研究,在腔体下部朝向站台方向设置进风口,能够明显提高候车厅的自然通风效果;腔体朝向室内单侧开口,自然通风效果优于双侧开口。在这一前提下,选取腔体截面边长(P1)、腔体高度(P2)为形态变量,腔体纵向布置数量(P3)、腔体横向布置数量(P4)为布局变量,腔体开口宽度(P5)、腔体开口高度(P6)、腔体开口距地高度(P7)为构造变量,这7项设计参数为模拟实验的输入变量(图3),取值数量及范围如表1所示。其中,腔体开口宽度(P5)选取与腔体截面边长的比值(开口系数)作为输入变量。
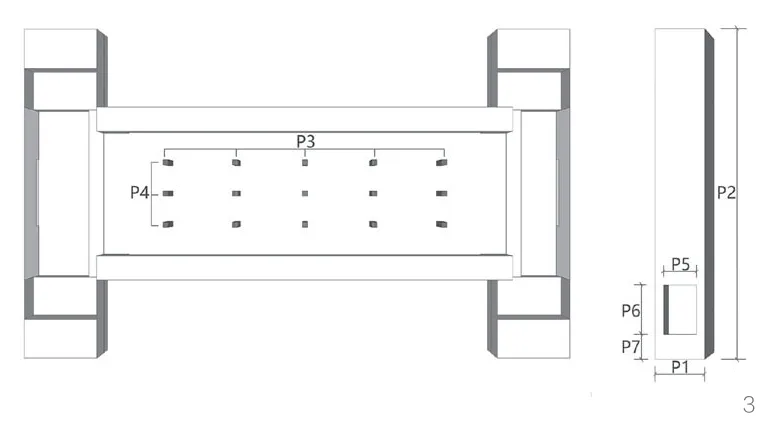
3 腔体设计自变量示意图
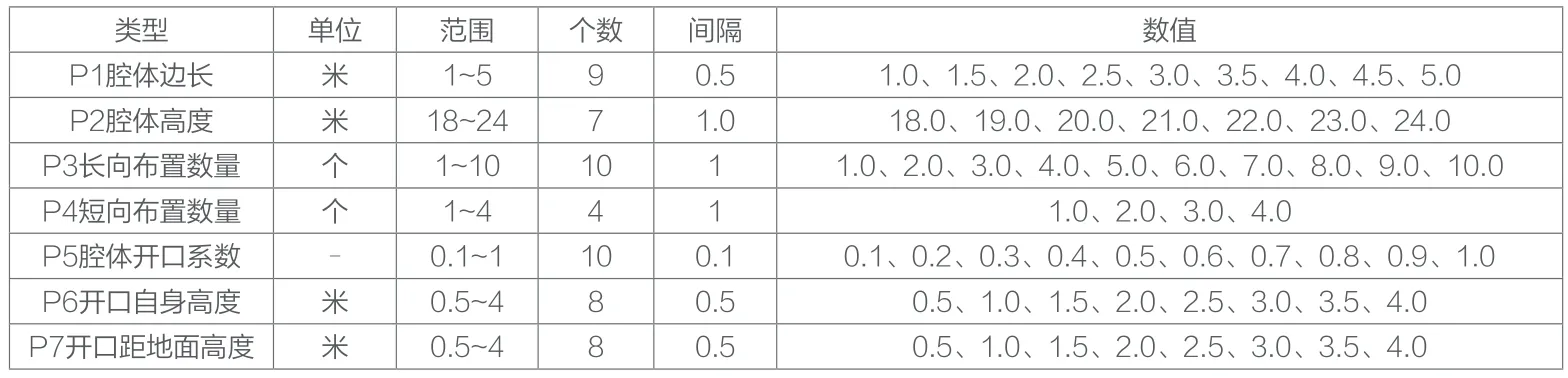
表1 腔体设计自变量及取值
2.2 模拟实验的因变量设置
首先,候车厅室内温度、风速对人体舒适度的影响最为显著,被列为模拟实验输出指标。其次,考虑到火车站人流密集和全天候运行的特点,候车厅室内的CO2浓度较高,对室内环境卫生和人体健康影响较大[9],也作为舒适度评价的输出指标。最后,由于大型火车站候车厅空间高,热分层明显[10],本次研究选取候车厅人体活动高度,即1.5m高度截面的平均温度(P8)、平均风速(P9)和平均CO2浓度(P10),作为大型火车站候车厅的舒适度评价指标。
2.3 模拟实验的分析方法
采用SPSS(Statistical Product and Service Solutions)软件的偏相关分析方法,选用显著性双尾检验Sig.(2-tailed)来判定自变量、因变量是否相关,选用皮尔逊相关系数(Pearson Correlation Coefficient)作为自变量与因变量之间相关性强度排序的依据。偏相关分析是在控制和排除了同一体系的其他变量影响情况下,描述一对变量影响关系的分析方法。在多变量偏相关分析中,控制变量个数为零时(不排除其他变量的影响),为零阶偏相关;控制变量个数为一时,为一阶偏相关,以此类推[11]。
显著性双尾检验Sig.值可以对相关性分析结果进行验证,低于0.01说明腔体自变量与舒适度因变量之间的关联可信度水平为99%,低于0.05说明自变量与因变量之间的关联可信度水平为95%,可进行相关性描述;Sig.值高于0.05说明自变量与因变量之间的关联可信度水平低,不可用于相关性描述[12]。
皮尔逊相关系数在自然科学领域用于度量两个变量之间的相关程度,其值介于-1~1之间。当随自变量的增加,因变量趋于增加,则皮尔逊系数为正,反之为负。相关性系数的绝对值大小在0.8~1.0之间为极强相关,0.6~0.8之间为强相关,0.4~0.6之间为中等强度相关,0.2~0.4之间为弱相关,0.0~0.2之间为极弱或者无相关。
3 模拟实验及输出数据
在CFD模拟实验平台中,对腔体植入设计的腔体边长(P1)、腔体高度(P2)、长向布置数量(P3)、短向布置数量(P4)、开口宽度(P5)、开口高度(P6)及开口距地高度(P7)7个自变量进行参数化组合,即7个自变量随机取值组合成为自变量组,每输入一组自变量,CFD实验平台对应输出平均风速(P8)、平均温度(P9)、平均CO2浓度(P10)3个因变量评价指标。为降低实验强度,利用Python编写程序,从7个自变量自参数化组合的896 000个数据组中进行科学抽样,共抽取200组自变量组合数据进行腔体通风模拟实验,对应输出200组候车厅P8、P9、P10舒适度指标。对这200组自变量、因变量组成的数据组进行相关性分析和显著性双尾检验,用来判断自变量的相关性显著程度和相关性强弱排序。
4 相关性分析
对200组腔体植入模拟实验数据,采取零阶偏相关、六阶偏相关分析比对的方式,揭示腔体植入7个自变量与3个舒适度因变量的关联。
腔体植入设计的P1~P7自变量与P8~P10因变量的零阶偏相关分析,操作方式分三步:1)选定一对自变量和因变量,如P1和P8,在不控制、不排除其余自变量(P2~P7)对P8影响的情况下,直接分析P1与P8的相关关系,导出皮尔逊相关系数;2)依次选取P2~P7自变量,逐一分析其与P8的相关关系,对应导出6个皮尔逊相关系数;3)分别以P9、P10为因变量,重复第一步、第二步做法,逐步完成P1~P7与P9、P10的相关性分析,导出相应的皮尔逊相关性系数(表2)。
建筑的自然通风是复杂的流体动力学系统,植入腔体的7个自变量对候车厅舒适度3个因变量的作用,亦非任何两个简单的自变量、因变量的相关性分析所能描述的。在充分考虑多个单变量之间相互作用的前提下,在对6个自变量的影响进行控制和排除基础上,利用六阶偏相关分析,揭示某一个自变量与因变量是否具有相关性和相关性的强弱,能够更加契合自然通风的本质。具体做法如下:当分析P1与P8~P10的相关性时,把P2~P7作为控制变量,考虑并排除这6个控制变量在P1对P8~P10相关性分析时的影响,导出P1与P8~P10的偏相关系数。其他6个自变量的偏相关分析以此类推,偏相关系数见表3。

表2 零阶相关性分析系数表
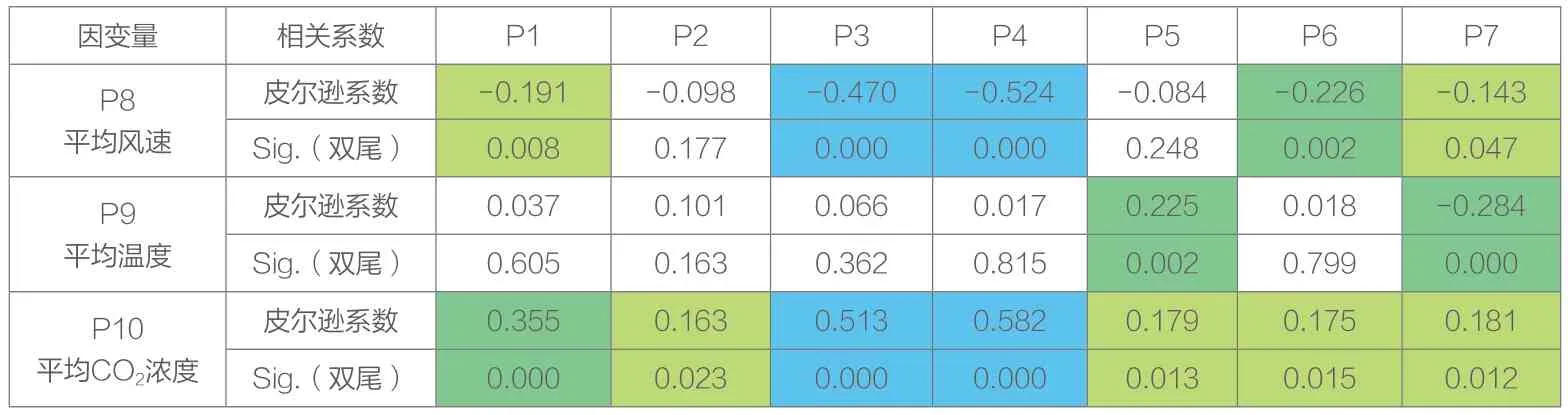
表3 六阶相关性分析系数表
4.1 相关可信度分析
从零阶偏相关系数表的显著性检验Sig.值可以看出,P3-P8、P4-P8、P5-P9、P7-P9、P1-P10、P3-P10、P4-P10的Sig.值低于0.01,表明自变量、因变量之间的关联可信度水平为99%;P2-P10的Sig.值界于0.01~0.05之间,表明自变量、因变量之间的关联可信度水平为95%。从Sig.值判断,上述8组变量为显著关联,可进行相关性描述。其余13组自变量、因变量的Sig.值均高于0.05,关联水平低,不可进行相关性描述。
从六阶相关性分析系数表可以看出,在零阶相关性分析的基础上,P1-P8、P6-P8、P7-P8、P5-P10、P6-P10、P7-P10等6组变量的显著性检验Sig.值均界于0.01~0.05之间,可信度水平均为95%,为显著关联,可进行相关性描述。
4.2 显著相关强度排序
从零阶偏相关系数看,P4-P8、P4-P10为中等强度相关,P3-P8、P5-P9、P7-P9、P1-P10、P3-P10为弱相关,P2-P10为极弱相关。从六阶偏相关系数看,相关强度整体上较零阶偏相关呈变大趋势,P3-P8、P4-P8、P3-P10、P4-P10为强相关,P6-P8、P5-P9、P7-P9、P1-P10为弱相关,P1-P8、P7-P8、P2-P10、P5-P10、P6-P10、P7-P10为极弱相关。
零阶相关性分析中,影响P8的自变量相关强度排序为P4、P3;影响P9的自变量排序为P7、P5;影响P10的自变量排序为P4、P3、P1、P2。
六阶相关性分析中,影响P8的自变量相关强度排序为P4、P3、P1、P6、P1、P7;影响P9的自变量排序为P7、P5;影响P10的自变量排序为P4、P3、P1、P7、P5、P6、P2。
六阶偏相关与零阶偏相关的强度相比,增加了新的自变量进入排序,整体排序大体一致,也证实了两种相关性分析的有效性。
4.3 显著相关数量分析
由表2,3还可以看出,P3、P4对P8、P10均有较高强度排序的影响;P5、P7、P1、P6对两个以上因变量具有由高至低多个排序的影响;P2仅对P10具有低强度排序的影响。因此,在腔体植入设计中应优先考虑P3(纵向布置数)、P4(横向布置数),之后是P5(开口宽度)、P7(开口距地高度),再次是P1(腔体边长)、P6(开口高度),最后是P2(腔体高度)。
4.4 显著相关正负分析
从皮尔逊相关系数的正负属性看(图4),P1~P7对P8均为负相关,随着自变量的变大,平均风速降低;P1~P7对P10均为正相关,随着自变量的变大,平均CO2浓度也增大;P1~P6对P9为正相关,P7对P9为负相关,随着自变量的变大,平均温度增大或减小。从候车厅舒适度评价目标看,为了提高风速、降低温度、降低CO2浓度,P1~P6的自变量具有同向作用,可一并优先选择利用。P7仅在考虑平均温度指标时,有条件选择利用。
4.5 关联度验证
设计一组模拟实验,对舒适度关联度较大的P4(横向布置数)、P3(纵向布置数)、P1(腔体边长)3个自变量进行相关性验证。试验中其他自变量取定值,P2=21、P5=0.5、P6=2、P7=2,保持腔体截面总面积为4.8m×4.8m=23.04m2。腔体自变量P4、P3、P1的取值以及利用CFD输出候车厅1.5m高度处风速、温度、CO2浓度云图,如图5所示。

4 正相关、负相关分析图
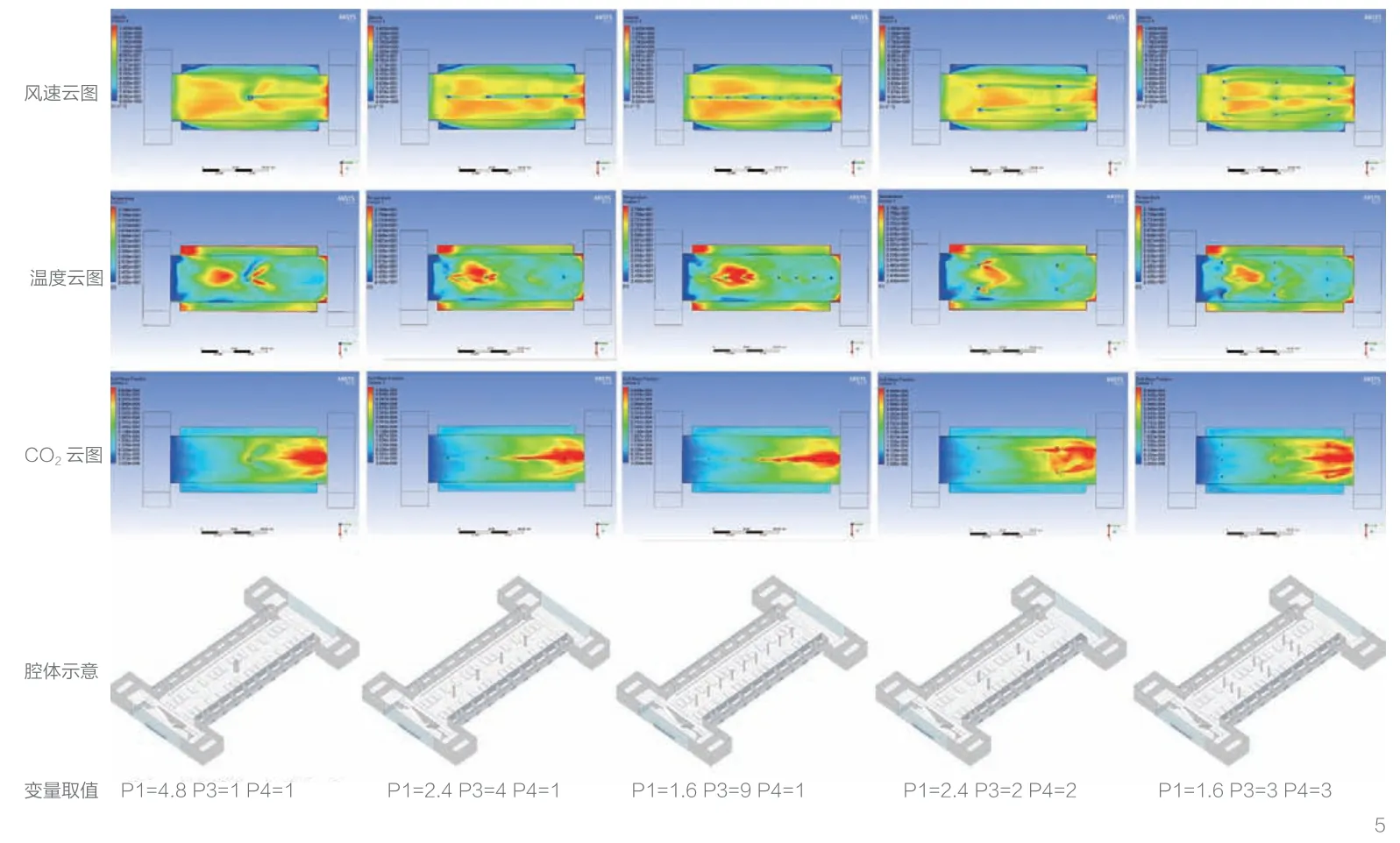
5 实验验证结果
分析云图发现,在腔体截面总面积一致的情况下,其他自变量取值不变时,通过控制P4、P3、P1的取值,风速、温度、CO2浓度的平均值和均匀度均出现显著变化,说明以上关联度分析结论科学准确。
5 结论
基于200组模拟实验数据进行的零阶偏相关、六阶偏相关分析,结果具有较强的耦合性;显著性双尾检验Sig.值、相关系数的正负和强度排序总体上也呈现出明确一致性和递进的关系,说明模拟实验及相关分析的科学性。研究结论如下:
(1)腔体设计参数与风速指标的关联性
影响候车厅平均风速(P8)的腔体自变量关联度排序为:P4、P3、P6、P1、P7。根据候车厅空间和流线要求,在方案设计阶段优先考虑腔体横向布置数量(P4)和纵向布置数量(P3);在深化设计阶段次选腔体开口高度(P6)、腔体边长(P1)和腔体开口距地高度(P7)。
(2)腔体设计参数与温度指标的关联性
影响候车厅平均温度(P9)的腔体自变量关联度排序为:P7、P5,在腔体设计的深化阶段予以重点考虑。
(3)腔体设计参数与CO2浓度指标的关联性
腔体7 个自变量均对候车厅平均CO2浓度(P10)有显著影响,关联度排序为:P4、P3、P1、P7、P5、P6、P2。设计策略与风速目标基本一致,即在方案设计阶段优先选择腔体横向布置数量(P4)和纵向布置数量(P3);在深化设计阶段次选择其他设计变量。
(4)基于风速、温度、CO2浓度综合指标的腔体设计策略
在候车厅方案设计阶段,重点考虑风速和CO2浓度两项舒适度指标,主要通过控制腔体纵、横向布置数量来实现;在候车厅和腔体深化设计阶段,重点考虑温度舒适度指标,兼顾风速、CO2浓度指标的完善,合理控制腔体开口的同时兼顾腔体边长的影响。
候车厅腔体植入设计策略的提出,是以腔体植入设计自变量、候车厅舒适度因变量的关联性阐释为手段,以定量数值分析为依据形成的理性判断。为了有效控制候车厅的舒适度水平,还需要从腔体设计变量的取值上着手,通过3项舒适度目标的交叉检验,实现建筑设计过程与舒适度水平的协同推进。
——与非适应性回归分析的比较

