临近空间高空气球囊体材料的蠕变试验和数值分析

张远平，姜鲁华，宋 林，吕 静，杨燕初

(1. 中国科学院光电研究院， 北京 100094； 2. 中国科学院大学， 北京 100049；3. 中国科学院高能物理研究所， 北京 100049)

临近空间主要是指大气层中的平流层，在对地观测、局部安防、移动通信等军民应用需求的强力推动下，临近空间持久区域驻留飞行器的发展受到世界各国高度关注[1-2]。在此高度可长时间飞行的飞行器有临近空间浮空器、太阳能无人机等。临近空间浮空器主要有平流层飞艇、高空科学气球等。高空科学气球是指工作在平流层高度区域的轻于空气的浮空飞行器，也称高空气球或者平流层气球[3]。由于高空科学气球飞行在平流层，飞行高度较高、对地观测范围较大、效费比高，因此在科学研究和军事方面都有很大的使用前景，目前美国、日本以及欧洲一些国家均在使用高空科学气球进行各项试验和研究。

临近空间浮空器囊体材料作为浮空器的主要材料，其性能直接影响浮空器的应用效能[4]，比如囊体可承受压力、有效载荷、使用寿命等。临近空间飞艇囊体材料一般由多层薄膜与高强纤维织物复合而成[5]，而高空气球囊体材料主要是聚乙烯薄膜为主的高分子薄膜材料。临近空间飞艇是目前的研究热点，对于其囊体复合材料的各类性能已经有了深入研究。高空气球目前应用不是很广泛，其研究相对于临近空间飞艇要少一些。NASA研究人员对高空气球进行了多次室内模型测试、材料测试及试飞试验，对于囊体材料的深入研究一度成为NASA高空气球的主要研究内容之一[6]。NASA还对3种不同设计的高空气球进行了囊体材料性能测试和耐压试验[7]。Henderson针对高空气球囊体材料Stratofilm372和AstrofilmE2分别建立了室温以及低温状态下的单轴蠕变屈服结构模型，用该计算模型可以直接从应力状态得到应变和变形[8]。美国德州的A&M大学提出了一种新的分析方法，动态机械分析法，利用动力学方法对常用薄膜类材料的黏弹性蠕变性能进行了试验分析，并建立了非线性结构模型[9]。杨希祥等对平流层长航时气球上升过程进行了分析研究，得出了囊体材料的物理参数带来的影响[2]。麻震宇等对临近空间浮空器囊体进行了超压特性和承载特性分析[10]。随着飞行任务复杂化，从零压型的高空气球逐步向长航时的超压型的高空气球发展，在长时间受压情况下，囊体材料会发生缓慢的蠕变。因此本文设计了蠕变试验，对临近空间高空气球囊体材料的蠕变特性进行了测试，结合试验结果对囊体材料进行了分析仿真，并给出了相关的蠕变模型参数。

1 蠕变试验

针对某型号高空气球囊体材料DPE-3进行研究，该材料由高分子材料组成，厚度为38 μm，呈透明状，断裂伸长率为512%。蠕变试验分为一、二、三组，拉伸强度分别为0.625 N/cm、1.25 N/cm、2.5 N/cm，每组试验6个试样。该材料经纬向强度基本一致，因此不区分经纬向，作为各向同性材料进行试验分析。

试验采用自行设计的蠕变试验架，如图1所示，在室温下进行蠕变试验。囊体材料试件被制作为哑铃型，有效试验长度为180 mm，宽度为20 mm，如图2所示。

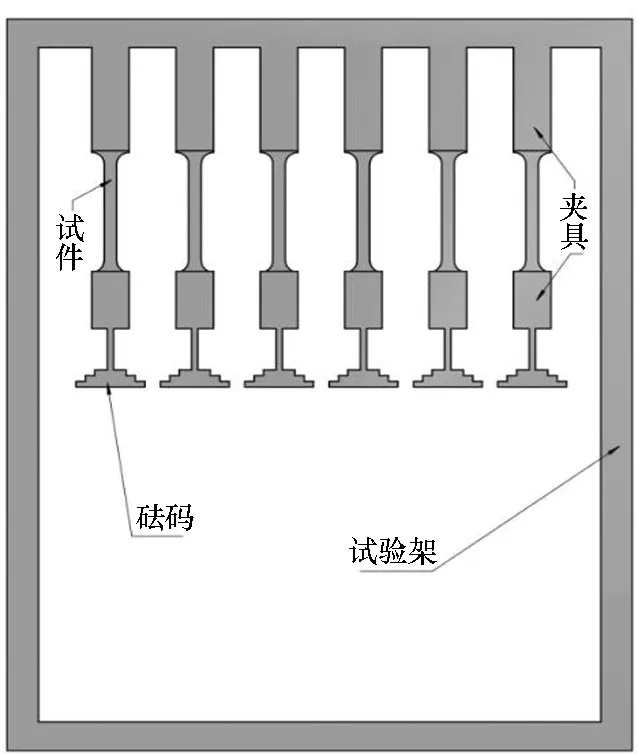
图1 蠕变试验架Fig.1 Creep test frame

图2 DPE-3囊体材料蠕变试验试件Fig.2 Creep test specimens of envelope material for DPE-3

将试件两端利用蠕变试验架中的特制夹具夹紧，下端夹具为轻型硬塑料，重量为0.5 N。以夹具重量0.5 N作为预张力确保样条处于垂直状态，并保持10 min，且将形变清零后加载至所需载荷，然后将时间清零，开始进行蠕变性能测试。在载荷的作用下，试件产生形变，记录下来的形变量(拉伸位移)即为蠕变量。

临近空间高空气球在超压设计状态时，会承受一定的内压。在开展本次蠕变试验之前，本项目组已进行多次超压型高空气球的实际飞行试验，根据实际承受的内压计算囊体材料的受力情况，其囊体材料承受的最小拉力在0.625 N/cm左右，工作拉力在1.25 N/cm左右，最大拉力在2.5 N/cm左右。

试验分别进行一、二、三组，根据球体实际受力情况，设置拉伸强度分别为0.625 N/cm、1.25 N/cm、2.5 N/cm。由于试件宽度为2 cm，则一、二、三组试验中每个试件的载荷分别为1.25 N、2.5 N、5 N。每组蠕变试验做6个试样。其中试验组一的第2和第4个试样以及试验组三的第5个试样在试验结束时发生明显的切向变形，原因是装夹不对称造成统一横截面所受应力不均匀，该三个试样的试验结果无效。

图3～5分别给出了常温状态下，三组蠕变试验的时间-拉伸位移实验结果和最小二乘法的拟合曲线。

(a) 试样1(a) Sample 1

(b) 试样2(b) Sample 2

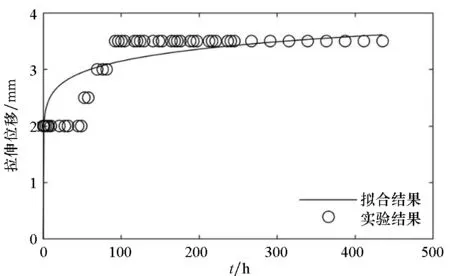
(c) 试样3(c) Sample 3

(d) 试样4(d) Sample 4

(e) 试样5(e) Sample 5

(f) 试样6(f) Sample 6图3 拉伸强度为0.625 N/cm的时间-拉伸位移曲线Fig.3 Time-tensile displacement curves of 0.625 N/cm

(a) 试样1(a) Sample 1

(b) 试样2(b) Sample 2

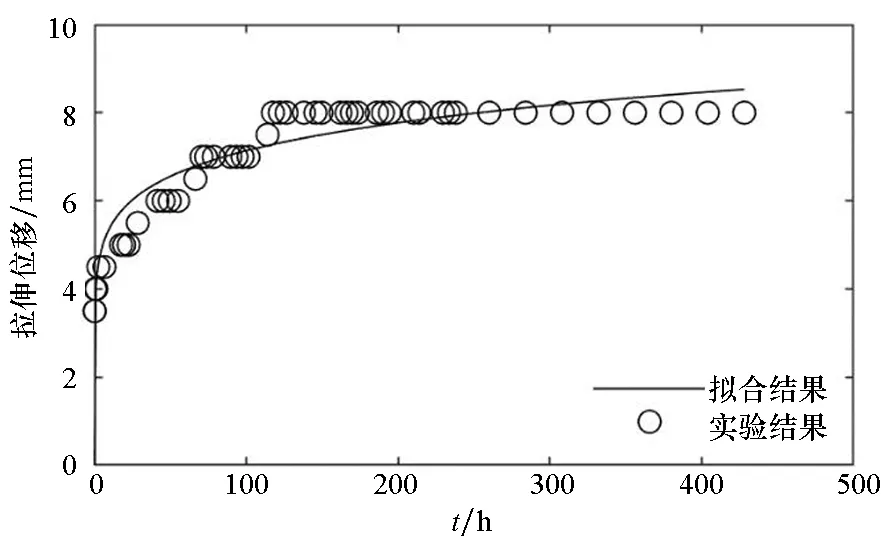
(c) 试样3(c) Sample 3

(d) 试样4(d) Sample 4

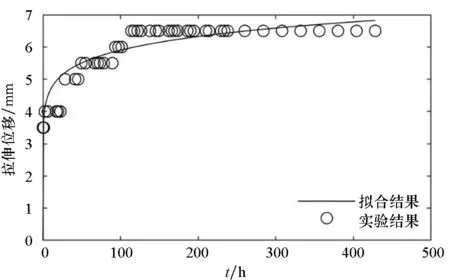
(e) 试样5(e) Sample 5

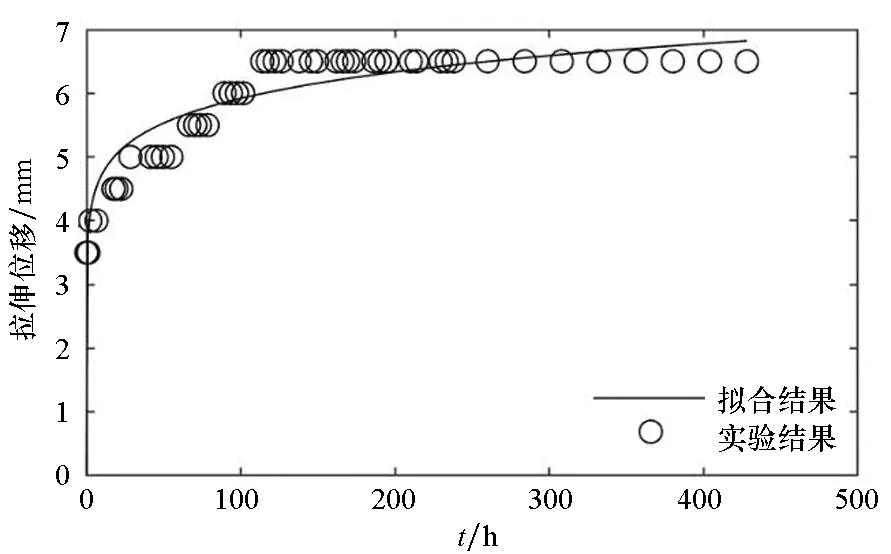
(f) 试样6(f) Sample 6图4 拉伸强度为1.25 N/cm的时间-拉伸位移曲线Fig.4 Time-tensile displacement curves of 1.25 N/cm

(a) 试样1(a) Sample 1

(b) 试样2(b) Sample 2

(c) 试样3(c) Sample 3

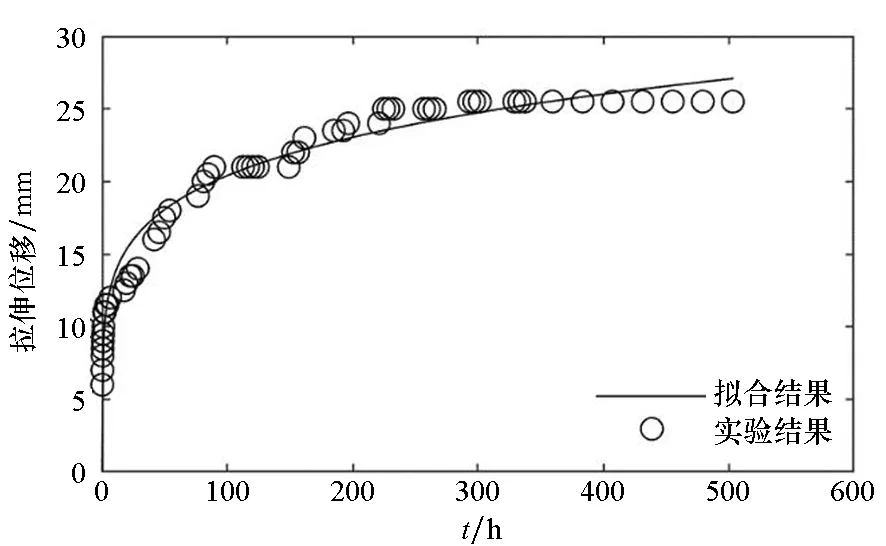
(d) 试样4(d) Sample 4

(e) 试样5(e) Sample 5

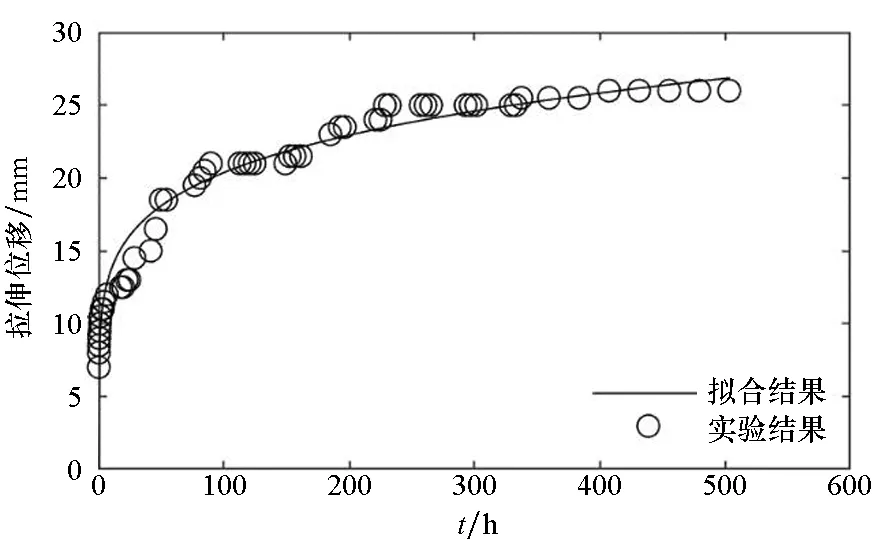
(f) 试样6(f) Sample 6图5 拉伸强度为2.5 N/cm的时间-拉伸位移曲线Fig.5 Time-tensile displacement curves of 2.5 N/cm

对图3～5的蠕变结果进行比较可以发现：随着载荷的增大，蠕变速率增大，蠕变量增大。高空气球囊体材料DPE-3由高分子材料组成，从高分子材料的结构来分析，在载荷增大的情况下，应力使得高分子材料内部松弛、折叠片松弛、界面滑移等情况更为明显，从而表现出蠕变量的增大。

因此，高空气球囊体材料DPE-3的蠕变性能跟载荷的大小有较为明显的关系：在小载荷情况下具有较好的抗蠕变性能；在载荷增大的情况下抗蠕变性能下降，蠕变速率增大，蠕变量增大。

2 陈化理论参数确定

根据陈化理论，在温度一定的情况下，材料蠕变的应变、时间和应力之间存在一定的关系ε=f(σ,t)。对于多数材料应力和应变之间存在较强的非线性关系，在变应力情况下，可以将蠕变的应变、时间和应力的关系表达为：

ε=Aσntm

(1)

式中，A、m、n均为材料参数，由蠕变试验的数据拟合进行确定。

将式(1)左右两边对t求导，可以得到：

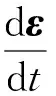
(2)

式中，A1=A·m,M=m-1。

根据陈化理论，将三组实验结果进行最小二乘法拟合，获得陈化理论参数A=0.002 541，n=1.676，m=0.153 2，A1=0.000 389 281 2,M=-0.846 8。利用这些参数，可以根据陈化理论计算囊体材料DPE-3的蠕变应变。

图6为利用陈化理论计算拟合的囊体材料DPE-3蠕变应变关于时间和应力的三维曲面图。根据陈化理论进行计算，可以得到囊体材料DPE-3在不同应力、不同蠕变时间下的蠕变应变，从而判断材料在该使用条件下的蠕变性能。

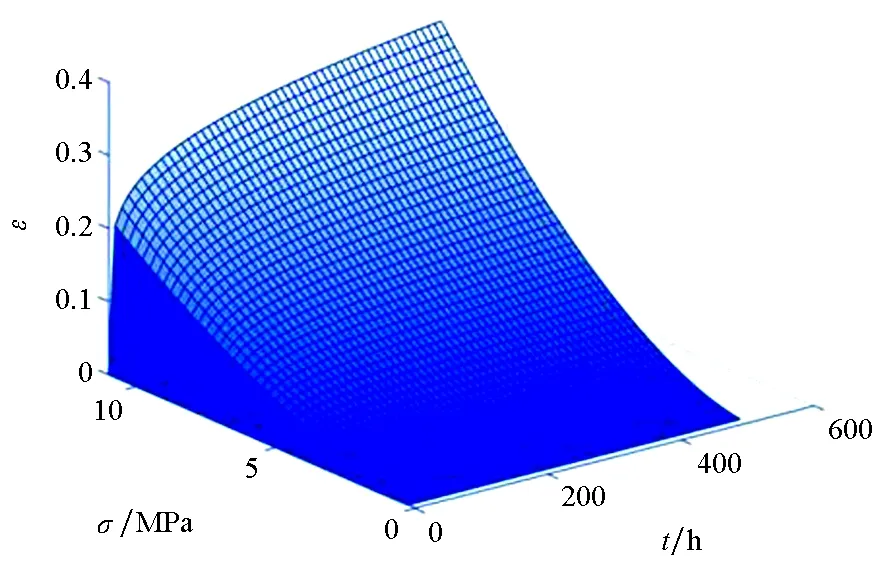
图6 蠕变应变关于时间和应力的陈化理论拟合三维图Fig.6 Three-dimensional fitting of creep strain with aging theory of time and stress

3 有限元数值分析

根据试验建立相应的有限元模型，对其用有限元分析方法进行蠕变计算分析，具体材料参数和几何参数见表1，将囊体材料DPE-3作为各向同性材料进行分析，与实际材料的属性相符。

蠕变模型选择陈化理论模型Norton，模型参数根据陈化理论确定，n=1.676,A1=0.000 389 281 2,M=-0.846 8。

陈化理论模型Norton是用全量形式进行描述，并且在方程中有时间参数t。陈化理论的表达形式适合于恒定的载荷或者变化非常缓慢的载荷。在浮空器的飞行过程中，由于囊体需要保持一定的压力，作用在囊体材料上的载荷变化比较缓慢，从蠕变状态来说符合陈化理论的主要特点。

分别进行三组有限元数值分析，试样一侧固定约束，一侧承受不同的拉伸力，载荷条件见表2。

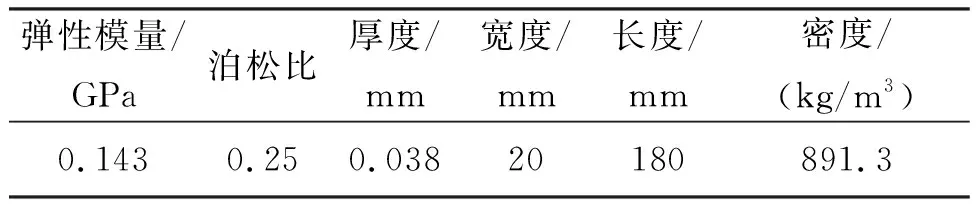
表1 有限元模型的材料参数和几何参数

表2 三组有限元模型的载荷条件

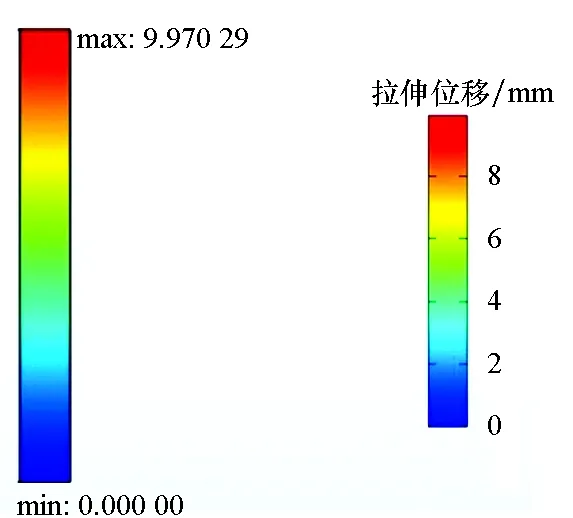
图7为不同载荷作用下，三组有限元分析试样经过400 h蠕变计算所得的拉伸位移。表3给出了对应三种工况下，试验、陈化理论模型计算和有限元分析获得的蠕变量。

(a) 0.625 N/cm

(b) 1.25 N/cm

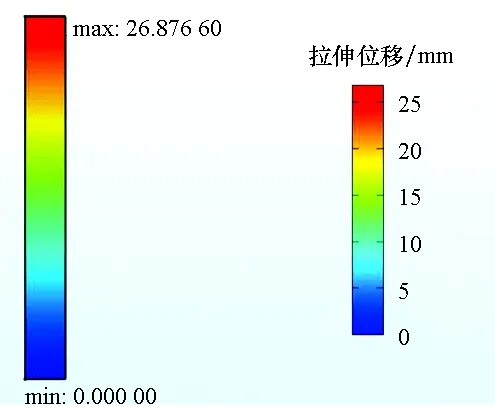
(c) 2.5 N/cm图7 不同拉伸应力条件下400 h后试样的蠕变量Fig.7 Creep of specimens after 400 h under different tensile stress conditions

表3 不同拉伸应力条件下400 h蠕变后材料试验、陈化理论和有限元分析的拉伸位移Tab.3 Tensile displacements of material test, aging theory and finite element analysis after 400 h creep under different tensile stress conditions

通过比较试验结果、陈化理论计算结果以及有限元分析结果可以发现：随着载荷的增大，蠕变量增大，蠕变速率增大。当载荷为该囊体材料实际承受的最大拉力时，陈化理论计算结果和有限元分析的结果都非常接近蠕变试验结果。

在小载荷的情况下，由于高分子材料在常温下处于玻璃态，链段都处于被冻结状态，并且受键长、侧基和键角等内部因素的影响较大，蠕变速率较小，蠕变量较小，同时蠕变量也容易不稳定。随着载荷的增大，蠕变速率增大，蠕变量增大，载荷成为蠕变量的主要影响因素，材料内部因素的影响减小，此时实际的蠕变试验结果更接近理论结果。

在载荷为0.625 N/cm、1.25 N/cm和2.5 N/cm三种实际受力工况下，陈化理论计算结果和有限元分析结果都比较接近实际蠕变试验结果，因此用DPE-3作为高空气球的囊体材料时，可以用本文的计算方法和有限元分析模型进行仿真和计算蠕变量，对材料的蠕变性能进行分析研究。

4 结论

通过蠕变试验给出了临近空间高空气球囊体材料DPE-3在不同应力下(0.625 N/cm、1.25 N/cm、2.5 N/cm)的时间-拉伸位移曲线，从试验结果分析可知，应力越小，蠕变速率越小，蠕变量越小，随着载荷的增大，蠕变速率增大，蠕变量增大。

根据蠕变试验数据，用最小二乘法进行曲线拟合，确定了囊体材料DPE-3的陈化理论参数。并以陈化理论建立了有限元分析模型，分析不同应力条件下(0.625 N/cm、1.25 N/cm、2.5 N/cm)蠕变时长为400 h的时间-拉伸位移结果。将陈化理论计算结果、有限元分析结果与蠕变试验结果进行比较，验证了陈化理论计算结果和有限元分析结果在一定程度上的准确性。本文的陈化理论计算方法和有限元分析模型，可用于分析和计算囊体材料DPE-3的蠕变性能，为临近空间高空气球的设计和分析提供参考。