潮致泥沙全沙净输运解析模式

储 鏖，徐 怡，陈永平，郁夏琰，王 彪

(1. 河海大学 港口海岸与近海工程学院，江苏 南京 210098; 2. 江苏省海岸海洋资源开发与环境安全重点实验室(河海大学)，江苏 南京 210098; 3. 中交上海航道勘察设计研究院有限公司，上海 200120; 4. 上海市环境科学研究院，上海 200233)

水流和底床相互作用的往往通过泥沙运动体现出来。而在河口、海岸地区的水下地形变化往往受到径流、潮流、波浪、人类活动等的影响，是河口泥沙在水动力驱动下输运的结果。在此类地区，潮流作用明显，周期性的潮波动力驱动的泥沙输运呈可逆和往复的特征，往往是滤除周期性作用后得到的泥沙净输运在很大程度上决定了河口动力地貌的改变[1-2]。以往的研究成果显示，潮波进入河口及浅海区域时，因水深、径流、地形等因素的影响发生变形，出现潮汐和潮流不对称现象[3]，其中潮流动力导致的不对称输运、潮泵等机制是泥沙净输运的主要组成部分[4-6]。

van de Kreeke和Robacczewska(简称VDK & R)研究了M0余流、M2、M4、M6、S2分潮流相互作用对粗沙净输运的影响，并提出粗沙净输运解析解[7]，该方法无需复杂模型，能够通过潮流分潮调和常数，即振幅和相位，快速、直观地计算泥沙净输运，其解析解亦揭示了在M0作用较小的海域，泥沙净输运仅与M0、M2、M4、M6有关。VDK & R进一步采用M0、M2、M4、M6分潮流组合和全分潮流组合代表潮波动力，驱动EMS河口水沙动力模型，其计算结果显示两者模拟得到的泥沙净输运差别不大。其研究成果被视作动力地貌模型中潮波动力概化的理论依据，即潮波动力为主的海域动力地貌模型中可单纯的考虑M0、M2、M4、M6分潮流的作用[2,8]。Song等研究了M2、S2、MS4分潮之间的相互作用对潮汐不对称的影响[9]。李谊纯从偏度出发，结合推移质泥沙输沙公式，推导了利用潮流调和常数估算河口推移质输沙的解析方法，经对比，解析方法与直接采用推移质输沙率公式结果一致[10]。Guo等研究了长江一维模型下径流和潮流不对称对地貌的影响，提出了受径流影响较大地区的河口在M0余流、M2、M4分潮流作用下的泥沙解析解净输运[8]。在以上及更多潮流对泥沙净输运影响的研究中，普遍认为M0、M2、M4分潮流相互作用引起的潮流不对称是潮平均泥沙净输运的主要成因[11-15]。

Chu等拓展了VDK & R对泥沙净输运解析解并在河口地区进行应用，提出了考虑M0余流，M2、M4、M6、S2、N2、MS4、MN4、K1、O1分潮流作用下的粗沙解析解净输运[16]，并指出分潮流的三重相互作用(M2,S2,MS4; M2,N2, MN4;M2,K1,O1)对粗沙输运有净的贡献，并且在河口地区各分潮流和M0的相互作用的贡献不可忽略。

现有有关泥沙净输运的解析解多基于粗沙输运为主的情形，虽然Guo等[8]提出了适用于全沙输运的公式，但该公式仅仅考虑了M0余流、M2、M4分潮流作用，与Chu等[8]的研究结论相悖，其计算结果与数值计算结果存在差异(见后文)。这里拟采用以Englund-Hansen经验公式为基础[17-18]，即全沙输运是流速的5次方的函数，考虑M0，M2、M4、M6、S2、N2、MS4、MN4、K1、O1等分潮流组合的作用，推导全沙净输运解析解。该公式可以反应河口地区泥沙粒径较细，泥沙输运以全沙输运为主的特征。此外，以推导的公式为基础，计算分析分潮流相互作用对泥沙净输运的贡献，确定泥沙净输运的主要驱动力。

1 潮致泥沙净输运解析解

在受潮汐波作用影响的河口海岸地区，水流和底床的相互作用，即泥沙输运呈周期性变化。因此，某一时刻甚至于某一时间段的泥沙输运并不能体现水流和底床的相互作用，往往需要通过时间积分，滤除周期性潮动力引起的波动性的泥沙输运，得到泥沙的净输运。滤除了周期性作用得到的泥沙净输运除了包含非周期驱动动力的贡献外，亦包含了具有不同周期的周期性驱动力相互作用的结果[7,16]。

现有大量关于泥沙输沙率及输沙率公式研究的成果，主要有动力学派、运动学派和能量学派，本研究基于能量学派的理论以及经验方法，假设输沙公式的一般形式为[7]：

S=f|u|nsign(u)

(1)

式中：S为单宽体积输沙率，m2/s；f为泥沙和流体特征参数，仅与泥沙和水的性质有关，不同经验公式取法不同；u为流速，m/s；n为指数。此处n的取值代表了不同的泥沙输移模式，适用于不同情况，当n=3时，适用于类似Bagnold推移质输沙率公式[20]；当n=5，则有Englund-Hansen全沙输沙率公式[18]。n采用采用奇数时，输沙率为流速的奇数阶函数，在潮周期内，当流速对称分布时，净输沙率为零；当存在潮流不对称等情况时，净输沙率不为零[10]。

河口及近岸地区的水流受潮流作用，往往呈往复流，流速可以表达为[4]：

(2)

式中：uM0为欧拉余流流速，m/s；ui为分潮流流速振幅，m/s；ωi为分潮流角频率，rad/s；φi为分潮流相对于M2分潮流的相位角。

式(2)等号两侧都除以M2分潮流速振幅，可得到：

(3)

本研究基于Chu等[16]的研究成果，拟采用分潮序列，表1中列出了用于拟采用的潮流分潮序列及其角频率和相位关系。

表1 潮流分潮序列Tab. 1 Tidal constituents set

将式(3)代入输沙率公式(1)并进行无量纲化，可得

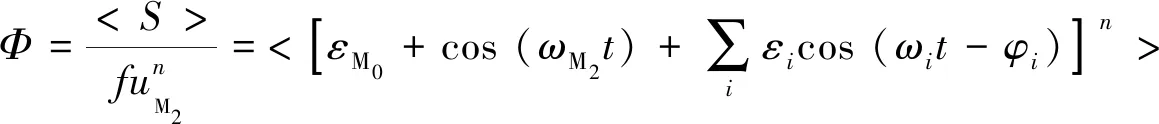
(4)

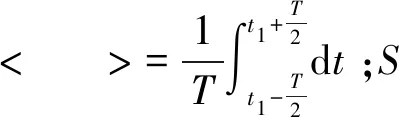
进行积分时，根据以往研究，假设两潮相互作用的角频率差值Δσ相关的余弦函数cos(Δσt)在积分时段内近似为恒定[7,16]，即：

(5)

其中，F为与角频率差值Δσ无关的余弦函数。

采用三角函数积分求解Φ，可以得到泥沙输运解析解。

VDK & R采用n=3，即考虑粗沙(底沙推移质)输运，研究了粗沙在M0、M2、M4、M6、S2分潮流相互作用下的输沙率，其认为在一般海岸地区M0的作用较小，并忽略了O(ε3)，得到的粗沙输运解析解结果共计5项，其中净输运有3项。Chu等[8]基于VDK & R的输沙率求解方法，在考虑M0余流，M2、M4、M6、S2、N2、MS4、MN4、K1、O1分潮流的情况下，提出了粗沙解析解输沙率计算公式，共计51项，其中净输运项15项。

而对于一般河口，如长江口，泥沙输运以细沙呈悬移质为主，以上适用于粗沙的解析解公式的适用需谨慎。通常认为，河口地区悬浮泥沙粒径较细，其运动形式主要以悬沙为主，而底床泥沙粒径分布较宽，泥沙运动形式兼有悬移质和推移质运动[21]，因此，河口海岸地区的泥沙输运应以全沙输运做考虑。因此，输沙率可取流速的5次方，即取n=5，采用经典的Engelund and Hansen公式计算输沙率精度较高[17]。

根据Engelund and Hansen输沙率公式[18]，输沙率可表示为：

(6)

式中：SE-H为E-H公式计算得到的单宽体积输沙率；Ss和Sb分别为悬移质和推移质单宽体积输沙率，m2/s；α为校正系数；U为流速，m/s；C为谢才系数，m1/2/s；Δ表示相对密度，Δ=(ρs-ρw)/ρw；D50为泥沙中值粒径，m。

类似于Chu等[8]的推导过程，本研究在考虑M0，M2、M4、M6、S2、N2、MS4、MN4、K1、O1分潮流的情况下，推导基于Engelund and Hansen公式的无量纲全沙净输运解析解表达式。潮致泥沙输运解析解公式中每一项都代表了分潮流之间的相互作用对净输沙率的贡献，这些相互作用可分为两种：第一种是恒定项，这些项不随时间变化，即对泥沙净输运有所贡献，共计129项；第二种是波动项，分潮流相互作用产生泥沙输运随着时间产生波动，对泥沙净输运没有影响，共有807项，限于篇幅，本研究列出对泥沙净输运有贡献的恒定项，公式见式(7)。

(7)

式中：Φi为根据相关分潮流对129个分项进行归纳整理得到的全沙净输运合并项，分别与11类不同分潮流相互作用有关。Φi表达式及其相关分潮流见表2。

表2 合并项表达式及其相关分潮流Tab. 2 Expression and related tidal constituent of Φi

(续表)

2 结果分析及讨论

如式(7)所示，本研究推导得到了的潮致全沙净输运公式，该公式相比以往的粗沙输运公式[7, 16]及部分全沙公式[8]有所改进，适用性更强。本研究首先通过设定相同的参数，采用不同泥沙输运解析解公式计算得到了解析解输沙率Φ，并将式(3)代入式(1)可以计算得到无量纲化输沙率数值解Φnumerical，通过对比解析解和数值解的计算结果，可对不同公式的结果进行对比以及验证本研究提出的解析解公式。此外，通过计算可以得到式(7)中每一项的值以及其对净输运贡献的占比，可以评估不同分潮流相互作用对净输运的贡献度即重要性。

2.1 不同输沙率公式的差异

首先，采用VDK & R[7]，Chu等[16]以及本研究的公式基于不同条件计算泥沙净输运的解析解结果，分析比较三个公式的计算结果和采用分潮流直接计算的数值解。主要分成以下两种情况进行讨论。

1) VDK & R经典假设改进：在VDK & R的经典假设基础上，考虑M0的影响，设定参数为：εM0=0.1，εM4=0.1，εS2=0.1，β=150°，其他参数均为零。计算结果如图1所示。图1(a)为粗沙输沙率的数值计算结果与解析解对比图；图1(b)为本研究的全沙输沙率解析公式和数值计算结果的对比图。从图1可以看出，当仅考虑M0、M2、M4、S2分潮流时，假设uM2=1.0 m/s，基于不同公式的泥沙净输沙率与数值计算结果吻合良好。该情况下，粗沙和全沙输沙率的净输运项相差不大，全沙解析解输沙率波动项绝对值稍大于粗沙。

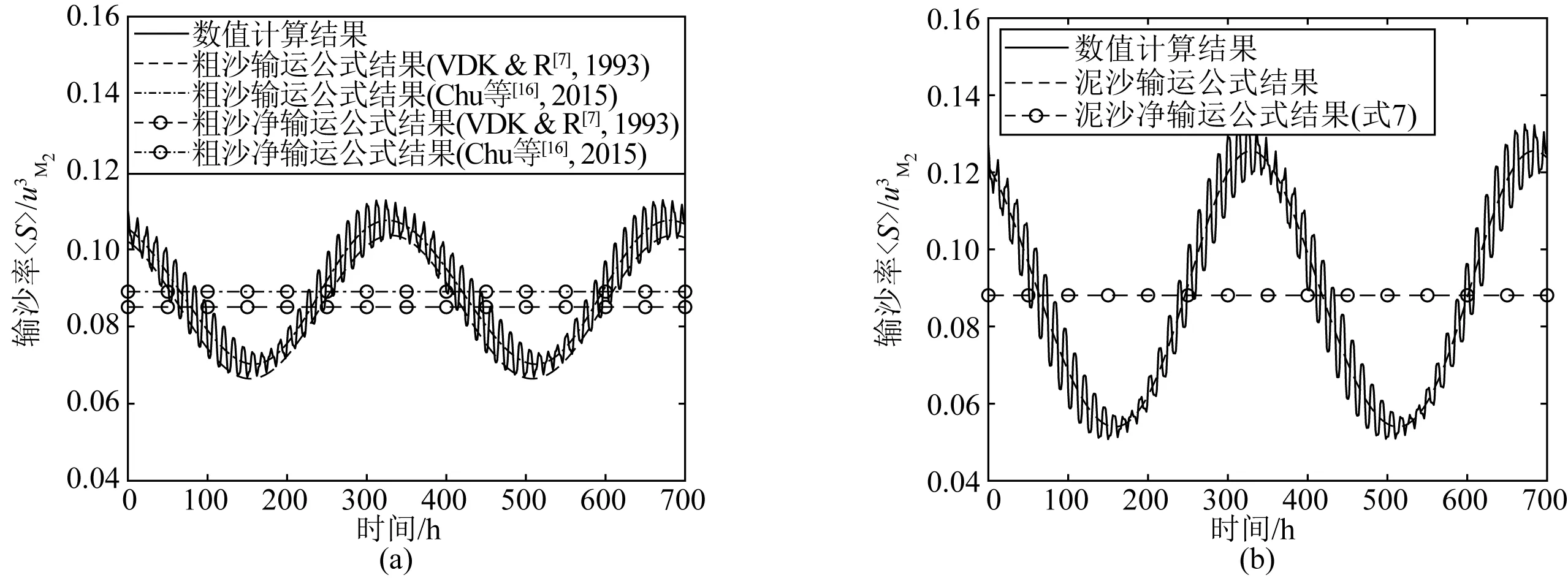
图1 假设情况下的泥沙净输运数值计算结果与不同公式计算结果对比Fig. 1 Comparison of calculated sediment transport based on different methods under the VDK & R assumption

2) 洪季长江口北槽：采用Chu等[16]对长江口北槽站点2004年洪季潮流调和分析结果进行计算，长江口典型站点调和分析结果见表3。假设uM2=1.0 m/s时，以表3的北槽枯季潮流速计算泥沙输运，计算结果如图2所示。从图2可以看出，该情况下不同公式的计算结果存在明显差异，采用本研究公式计算得到的全沙净输沙率是粗沙净输沙率的3倍。对比两者公式亦可发现，全沙公式中由于n的取值不同导致分潮流组合的增加是造成两者输沙率差异的原因。大、小潮差异明显：即大潮海向输沙率较大，小潮时期较小。采用全沙输沙率公式时，相邻的大潮的输沙率之间差异显著于其他公式的结果，两次小潮期间，两式计算得到的输沙率均较小且接近于零。

表3 北槽及徐六泾站点潮流分潮振幅及相对于M2的相位差Tab. 3 Amplitude and phase difference of tidal constituents relative to M2 at North Passage and Xuliujing station

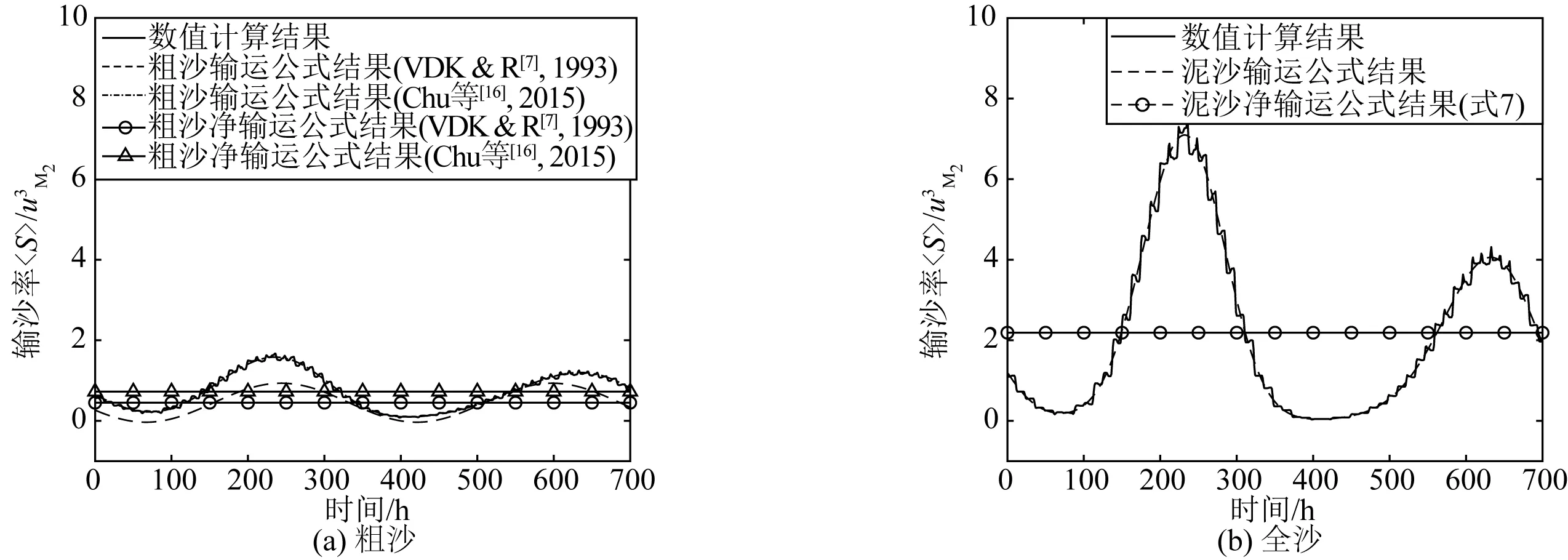
图2 北槽枯季泥沙净输运数值计算结果与不同公式计算结果对比Fig. 2 Comparison of calculated residual sediment transport at the North Passage of the Yangtze estuary (dry season)

采用三个不同公式，可以计算得到以上两种情况各分潮流相互作用对净输沙的贡献，结果见表4。由表4可以看出，无论采用何种公式，不同的分潮流相互作用对泥沙净输运的贡献表现不尽相同。在改进的经典假设情况下，涉及S2分潮流的潮潮相互作用对泥沙净输运的贡献较少，M0、M2分潮流相互作用导致泥沙的海向输运，M4、M2的相互作用占比较大。考虑洪季长江口北槽实际条件时，由于潮流不对称作用(90°<β<180°)，导致了泥沙的陆相输运；粗沙输运公式，即VDK & R[7]和Chu等[16]公式中，M0、M2相互作用是主要贡献项。此外，基于Chu等[16]公式和本文公式，都可以发现S2、MS4、M2和M0、S2相互作用对输沙率的贡献不可忽视。

表4 不同公式的分潮流组合对泥沙净输运的贡献率Tab. 4 Contribution of interaction of tidal constituents of different formulas

其次，本研究对比了Guo等[8]公式和本研究公式的差异。

同样采用Engelund and Hansen，Guo等[8]对长江口全沙净输运也进行了初步的研究，其考虑了M0余流、M2、M4分潮流对泥沙净输运的影响，推导出全沙净输运解析解公式，见式(8)。

(8)

Guo等[8]提出的式(8)仅考虑了余流和M2、M4分潮流的影响，共计6项。采用同样的假设，在仅考虑余流和两个分潮流的影响时，式(7)可以简化为9项，见式(9)。相较于Guo等[8]的公式，多了3项M0、M2、M4相互作用对泥沙净输运的贡献。

(9)

采用表3中北槽站点枯季参数，首先计算仅考虑M0余流、M2、M4分潮流时，假设uM2=1.0 m/s，εM0=0.28，εM4=0.1，β=294°，其他参数均为零，图3(a)给出了计算结果；图3(b)则给出了考虑所有分潮流计算结果。

由图3(a)可知，当仅考虑M0余流、M2、M4分潮流时，Guo等[8]提出的净输沙率公式计算结果与泥沙净输沙率数值计算结果有所差异，误差约为5%，采用式(9)计算得到的结果与数值计算的结果吻合更贴切，在某种假设条件下，Guo等[8]的公式亦可以用来计算泥沙的净输沙率。但实际上，正如Chu等[16]早已证明，分潮流的三重相互作用(M2,S2,MS4; M2,N2, MN4; M2,K1,O1)对泥沙净输运有贡献，包括了粗沙输运以及全沙净输运并且在河口地区各分潮流和M0的相互作用的贡献不可忽略。如图3(b)所示，当考虑M0余流，M2、M4、M6、S2、N2、MS4、MN4、K1分潮流时，本文公式的计算结果与数值计算的结果吻合良好，而采用Guo等[8]的公式得到的输沙率明显偏小，且仅为本文公式(7)结果的1/3，并且与数值解的中值相差过大。由此，Guo等[8]的简易公式一般不适合实际的河口海岸地区，在实际应用中，采用式(8)计算河口泥沙净输运需慎重。

图3 假设情况和实际站点的泥沙净输运数值计算结果与不同公式计算结果对比Fig. 3 Comparison of calculated residual sediment transport based on different methods at Beicao (dry season)

2.2 分潮流相互作用对净输沙率的贡献

采用式(7)可利用潮流分潮调和常数不仅可以直接快速计算净输沙率，还可以针对式中每一项不同分潮流及其相互作用对泥沙净输运的贡献进行研究，确定对不同径流强度、分潮流振幅、相位对泥沙净输运大小及方向的影响。以往研究发现有些分潮流之间相互作用(如M2，M4相互作用)对泥沙净输运影响较大，而有些相互作用仅对泥沙输运产生波动性影响，在进行潮周期平均后对泥沙净输运无贡献作用，这些都可以通过式(7)进行分析和计算。

表4为了对比不同公式的差异，仅仅列出小部分的分潮流相互作用，由表4可以看出不同分潮流之间的相互作用对净输沙的贡献不甚相同。为了较为全面的分析不同分潮流相互作用对输沙率的贡献，分析计算了不同径流条件下的各分潮流相互作用，即采用表2中Chu等[16]对长江口北槽和徐六泾站点2004年的洪、枯季潮流调和分析结果进行计算。表5中列出了对净输沙贡献率超过1%的余流分潮流组合贡献项及其贡献率。

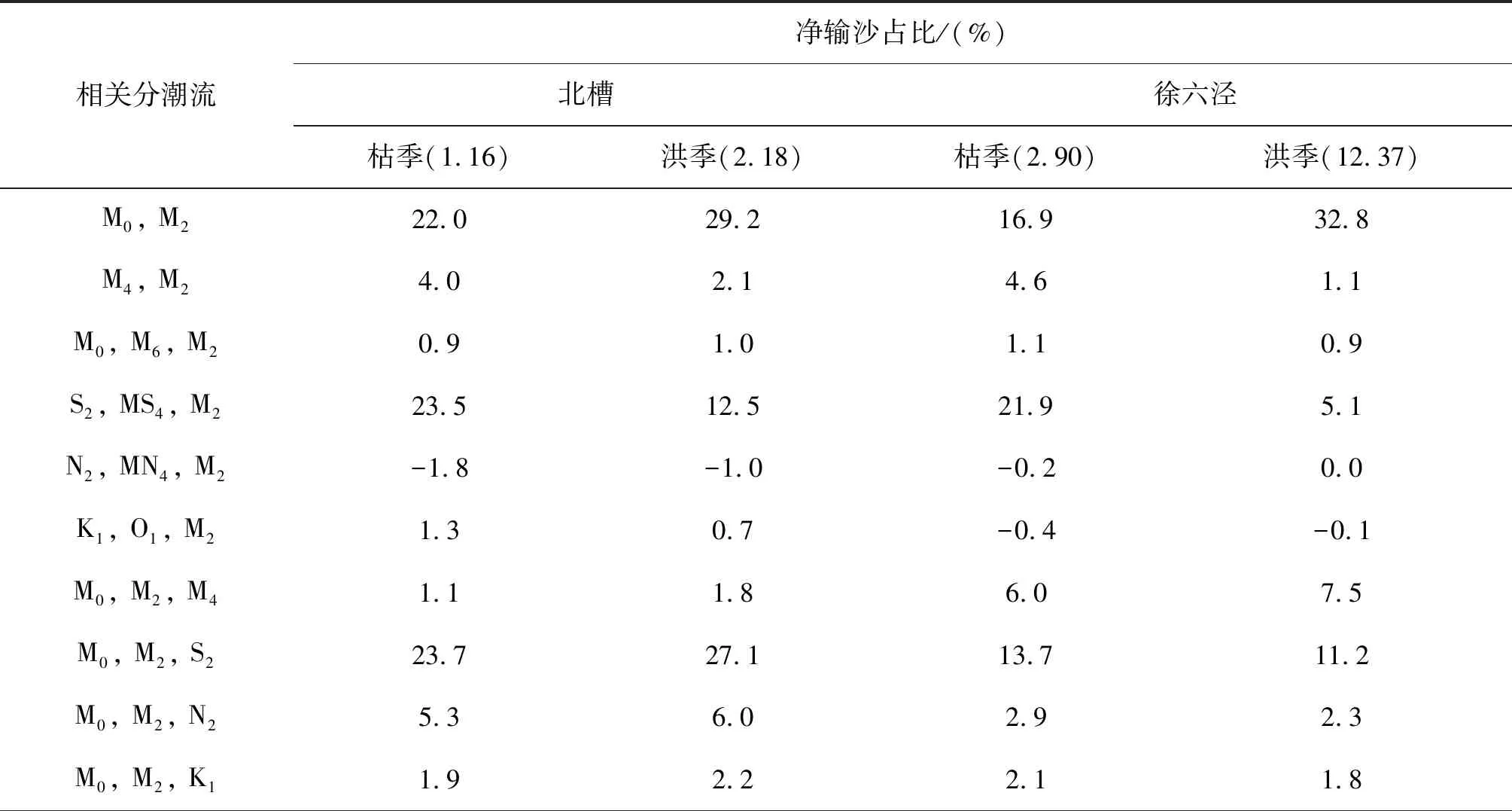
表5 分潮流组合对泥沙净输运的贡献Tab. 5 Contribution of interaction of tidal constituents

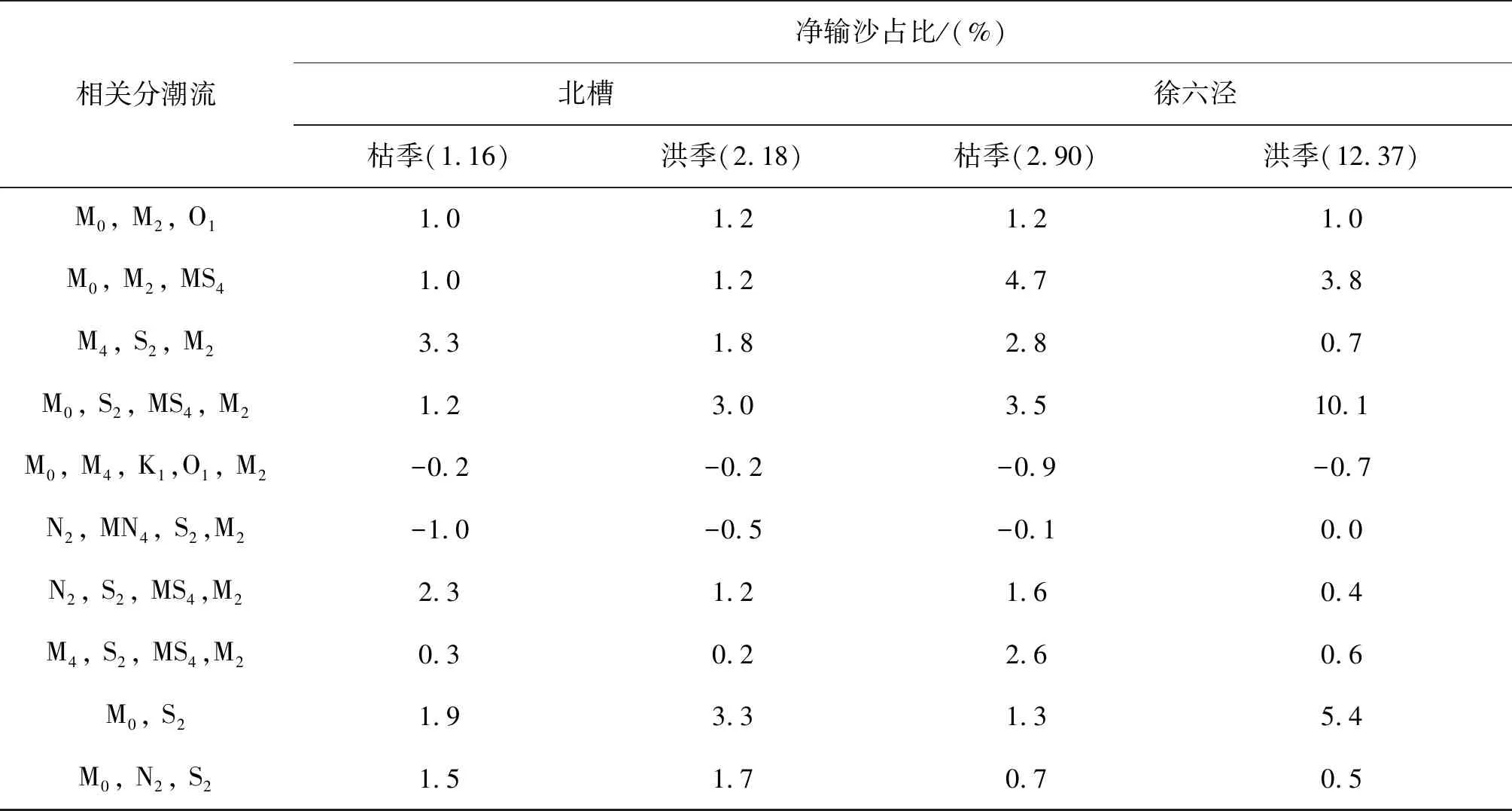
(续表)

1) 主要贡献项：由表5可看出，在北槽中部，两潮(M0、M2)相互作用，三潮(S2、MS4、M2)和(M0、S2、M2)相互作用对净输沙率的贡献较大，枯、洪季贡献率均达到68%以上。而相较北槽站点，位于更上游的徐六泾站点，倍潮相互作用的贡献率明显增加，如：三潮(M0、M4、M2)相互作用在徐六泾约为6%～7.5%；在北槽则是1%～2%。

在以往的研究中，往往认为潮流不对称(M2和M4相互作用)对泥沙净输运的贡献较大，本研究发现，在长江口典型站点三潮(S2、MS4、M2)相互作用对泥沙净输运的贡献显著高于两潮(M4、M2)相互作用。比较各分潮流与M0、M2相互作用对泥沙净输运的贡献，M0、S2、M2相互作用对泥沙净输运的贡献显著高于M0、M4、M2相互作用，且M0、S2、M2相互作用的贡献与相位无关，M0、M4、M2相互作用与M4、M2相位差β有关。该结果表明在受径流影响较大的河口地区，S2及其倍潮相互作用、余流与其他分潮流相互作用对泥沙净输运的贡献较大且不可忽略，在分析潮流不对称及泥沙净输运问题时应考虑除M4、M2以外更多的分潮流以全面分析不同分潮流组合的影响。

2) 季节变化：洪枯季径流量变化对泥沙净输运的影响较大。通过比较表5中两站分潮流相互作用贡献在洪枯季的变化，可以看出随着洪季M0增大，与M0相关的分潮流相互作用对泥沙净输运的贡献均有所增长。与余流无关的潮流分潮组合导致的泥沙净输运值不变，使得其对总泥沙净输运的占比即贡献显著减少。由于徐六泾站点洪、枯季节余流变化更大，其相互作用的贡献率变化也更大。不同的余流与分潮流相互作用贡献率对余流变化的响应有所不同，由表5可以看出，M0、S2相互作用对余流变化的响应比M0、M2相互作用显著，即M0变化对M0、S2相互作用的影响更大。

3) 相位对输沙率的影响：部分分潮流相互作用的泥沙输运方向取决于分潮流之间相位差，如表5所示，观察三潮(K1、O1、M2)相互作用的贡献率可以发现，在北槽站点产生的是向海方向的泥沙净输运，而在徐六泾站点产生的向陆方向的泥沙净输运。该相互作用贡献项由公式中的3个分项组成，具体表达式如下：(15εK1εO1cos(α5+α6))/4+(15εK13εO1cos(α5+α6))/4+(15εK1εO13cos(α5+α6))/4，可得该相互作用的泥沙净输运方向取决于K1、O1与M2相互作用的相位差之和，即α5+α6。

对于部分分潮流相互作用，分潮流之间的相位差对其贡献项的大小也有影响。例如(15εS2εMS4cos(α1-α3))/4为S2、M2、MS4分潮流相互作用的贡献项，其大小和方向与S2、MS4之间的相位差α1-α3有关。

除此之外，还有部分分潮流相互作用，其贡献项的大小方向与分潮流之间的相位差均无关。例如(15ε0εS22)/2为M0、S2、M2相互作用产生的贡献项，且和S2、M2之间的相位差α1无关。

因此，采用不同地区的分潮流相位参数计算得到的净输沙率差异较大，且每一项净输沙率贡献项对相位差的反应都不同。

3 公式验证及应用

采用长江口三个站点2016年7月21-22日、27-28日大小潮期间流速及潮输沙率资料对公式进行验证，三个站点分别位于南港、北槽、南槽的1#(31°20.32′N，121°40.26′E)、2#(31°14.75′N，122°1.60 ′E)、3#(31°7.79 N′，121°53.70′E)三个测站，站点位置分布见图4。

由于缺乏较长的实测流速资料，本研究利用基于Delft 3D的长江口二维水动力模型[16]进行模拟得到一个月的流速资料。并将流速在涨急、落急流速的方向上进行分解，并利用基于T-Tide的调和分析工具包进行调和分析计算得到分潮流调和常数，进而可采用式(7)计算可得到解析解净输沙率Φ。

采用如图4所示站点的模型模拟流速，可以直接代入E-H公式计算得到经验输沙率SE-H，计算时，取ρs=2 650 kg/m3，糙率n=0.013[19]。泥沙中值粒径选取可根据实测的粒配曲线(见图5)，根据图5取3个站点的D50分别为0.011 3 mm、0.011 mm、0.010 7 mm。

图4 站点位置示意Fig. 4 Location of stations

图5 站点悬沙粒径累积曲线图Fig. 5 Grain size accumulation curve of suspended sediment at different stations

对比计算得到的解析解输沙率Φ、基于模型结果的E-H公式经验输沙率SE-H以及基于实测流速和含沙量计算得到的实际输沙率Sobs作对比，结果见图6。

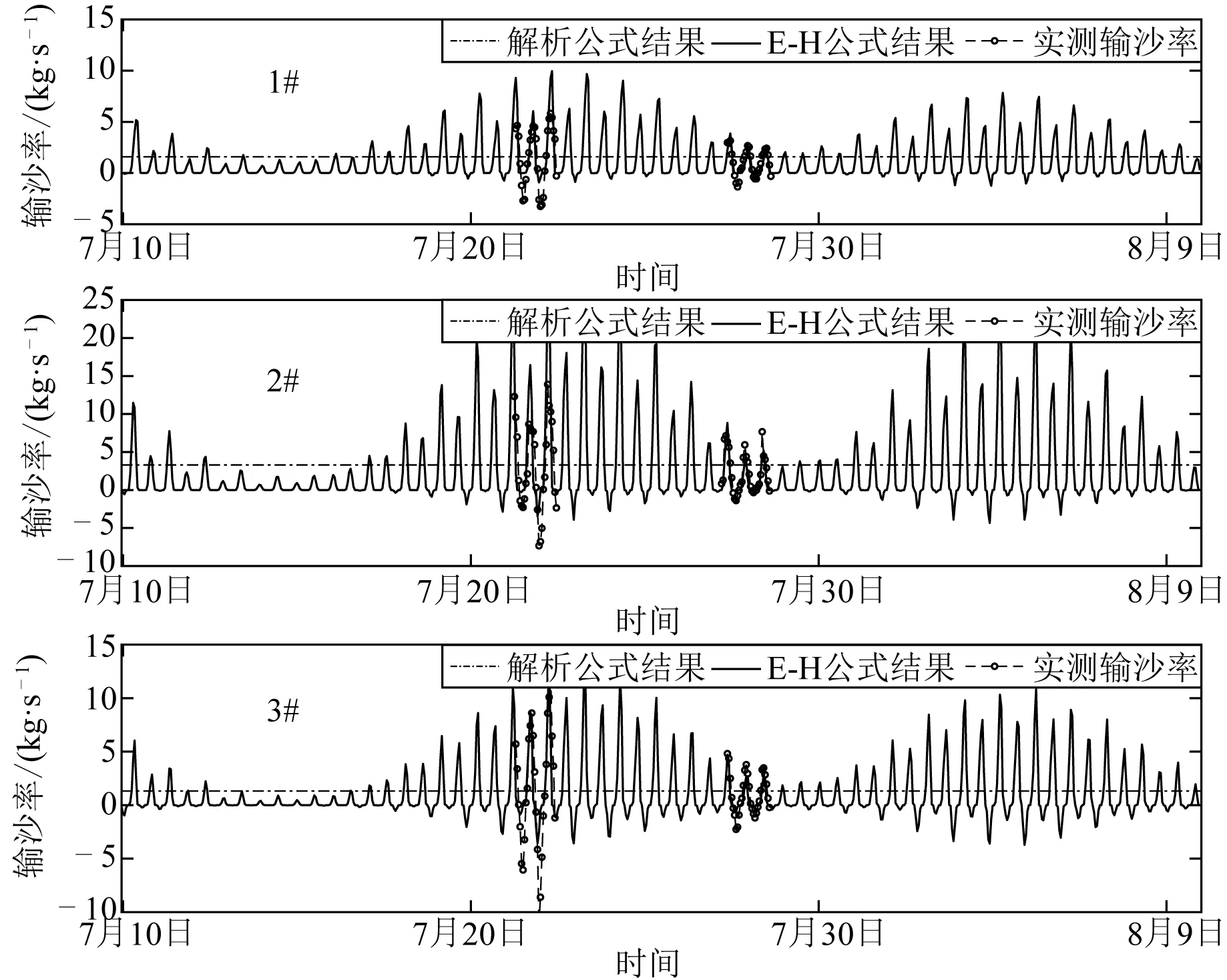
图6 输沙率公式验证结果Fig. 6 Verification on formulas of sediment transport rate

由图6可以看出，采用E-H公式基于模型模拟流速计算得到的经验输沙率和基于实测流速和含沙量得到实测输沙率基本吻合，说明E-H公式在该河口可以适用，此外E-H公式结果与解析公式结果吻合较好。大潮期间涨急时刻E-H公式输沙率绝对值高于实测输沙率，但落急时刻则低于实测输沙率。因此与实测输沙率相比，基于E-H公式的解析解净输沙率与实测数据基本吻合，但略微偏高，误差的可能原因是文中研究的净输沙公式未考虑起动切应力的影响。

4 结 语

以Engelund-Hanson公式为基础，即泥沙输运与流速的5次方成正比，假设河口地区水流以往复流为主，通过潮周期时间积分推导得到了潮致泥沙全沙净输运公式。该公式考虑了多分潮流情况下的全沙输运，完善并改进了已有研究提出的公式，拓展了潮致泥沙解析解的适用范围。通过该公式可以利用潮流分潮流调和常数直接计算泥沙净输运，分析分潮流和余流产生变化时对输沙率的影响，研究各分潮流及其相互作用与泥沙净输运之间的关系。主要结论如下：

1) 公式计算结果与数值计算结果十分吻合，表明净输运公式的正确性。与已有的泥沙粗沙净输运解析解比较发现，在长江口典型站点情况下，本文公式计算得到的净输沙是粗沙净输沙的3倍左右；大、小潮时期输沙率差异较大，两次相邻大潮的输沙率之间存在显著差异；两次小潮期间，两式计算得到的输沙率均较小且接近于零。对比Guo等[8]的全沙净输运公式，本文的公式更加完善，适用性更广。

2) 研究发现在长江口区域，潮不对称作用(S2、MS4、M2)和三潮相互作用(M0、S2、M2)等的相互作用对泥沙净输运的贡献显著高于通常意义上的潮流不对称、即两潮(M2和M4)相互作用对泥沙净输运的贡献，该结果可适用于受径流影响的半日潮河口地区。

3) 余流、分潮流的相互作用对泥沙输运的贡献率随着洪、枯季变化有所不同。洪季时，与M0相关的相互作用对泥沙净输运的贡献均有所增长，其对总泥沙净输运的占比即贡献显著增大。

4) 分潮流相互作用对输沙的贡献大部分表现为受M0控制，即向海输运，但是部分潮潮相互作用对泥沙输运的贡献其方向取决于分潮流之间的相位差，即可能会导致向岸输沙，而输沙率的大小由分潮流振幅和相位差共同决定。

文中得到的泥沙净输运解析解公式建立在输沙率与流速的五次方成正比的经验公式基础上，该公式适用于部分河口，未考虑河流中的泥沙过饱和和不饱和现象，且输沙率还与起动切应力等因素有关，文中假设该因素在一段时间内为不变量，未考虑该因素变化对泥沙净输运的影响，这些都会影响到泥沙的净输运，需要进行进一步的研究。