圆锥曲线中“设点热”后的点差法命题背景探究

◇ 山东 李 佳

解析几何的命题背景众多,究其原因会发现是解析几何的二级结论颇多,且各类推导运算量颇大.本文节选了解析几何中的一大热点——“点差法”,剖析“点差法”命题背后的本质,并对教学中的相关问题进行反思.

1 命题的背景和原则

解析几何是高中数学课程中的经典内容,而圆锥曲线更是解析几何中的重要曲线,它充分体现了解析几何的基本思想,是高考的必考内容,这类问题往往以把关题的形式出现.在《2019年浙江高考数学考试说明》里对圆锥曲线的考试要求中也提到：会解决直线与椭圆、抛物线的位置关系的问题;了解方程与曲线的对应关系,会求简单的曲线方程.

结合高中数学核心素养,在圆锥曲线的试题中,主要考查学生的逻辑推理、数学运算、直观想象这三个核心素养.因此关于圆锥曲线的试题,其综合性比较强,可以有效考查学生分析问题及解决问题的能力.本文将结合命题的相容性、准确性、多元性等原则,以“设点热”后的点差命题为例,谈谈笔者对命题设计的理解.

2 真题呈现

例1(2019 年浙江卷)如图1 所示,已知点F(1,0)为抛物线y2＝2px(p＞0)的焦点,过点F的直线交抛物线于A,B两点,点C在抛物线上,使得△ABC的重心G在x轴上,直线AC交x轴于点Q,且点Q在点F右侧,记△AFG,△CQG的面积分别为S1,S2.

图1

(1)求p的值及抛物线的准线方程;

分析高考中关于圆锥曲线的命题视角有很多,在这之中又以椭圆、抛物线与直线的位置关系的命题居多.在求解此类问题时,我们一般的解题思路为“设线”或“设点”,那么在具体的运算过程中,到底是选择设线好,还是选择设点好呢?

解(1)p＝2;抛物线的准线方程为x＝－1.

(2)因为y2＝4x,设A(t2,2t),由焦点弦性质得：xAxB＝1,所以

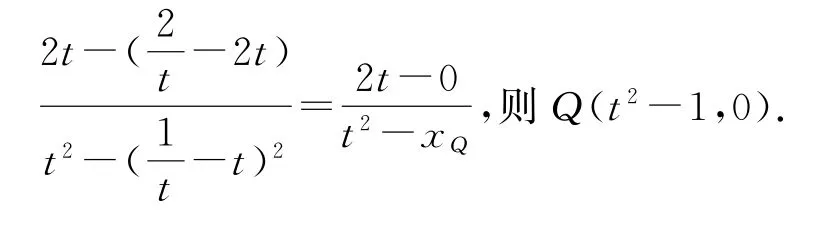
所以

当且仅当(x－2)2＝3时等号成立,解得或即代入则G(2,0).

从抛物线的命题角度来考虑,为什么在抛物线中“设点”更好呢? 那是因为在抛物线上,设A(x1,y1),B(x2,y2),直线AB与x轴交于点E(x0,y0),则总有x1x2＝x20,所以在抛物线中,点与点之间是有非常明确的一个定量关系,这就是为什么我们在研究抛物线与直线位置关系的相关题目时喜欢用“设点”来研究.

自从文科和理科合并以后,抛物线的引入,引起了一场“设点热”,因此同样的一个想法,我们能不能在椭圆或者双曲线中也用设点来研究呢?

3 椭圆和双曲线中“设点”做法的研究

椭圆和双曲线中点的研究,又往往和向量关联在一起,从而想到对定比点差法的研究.

定比点差法的原理：假设A(x1,y1),B(x2,y2)是椭圆上不同的两点,且不关于坐标轴对称,并且则

又因为

这里考虑到①②的结构,我们对③④进行降维处理,③－λ2可得

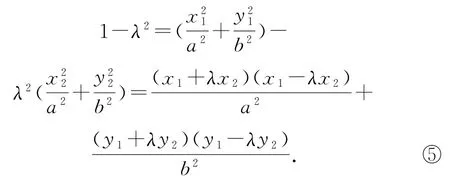
关于定比点差法的研究,目前对这个问题已经出现了两类经典问题,一类就是比例系数特殊化,即对点差法的理解与应用,还有一类就是定比分点特殊化,即圆锥曲线中的一个定点、定值问题.

3.1 演绎推理(1)——比例系数特殊化

考虑比例系数特殊化,即当λ＝1时,式子⑤为

整理即得

这个实际上就是点差法.

从代数角度来看,“点差法”实际上可以看成是定比点差法的一种特殊情况,而更深层次来看更是一种消元思想的体现.

假设D是线段AB的中点,则,设kAB＝k,则

根据端点关系来消元,在运算过程中可以消掉变量y1,y2.

例2椭圆的上顶点为B,右顶点为A,作一条平行于AB的直线l交椭圆于C,D两点,记AC与BD的斜率分别为kAC,kBD,求kAC·kBD的值.

解析

根据题设可得：B(0,1),A(2,0),C(x1,y1),D(x2,y2),则,

从而

3.2 演绎推理(2)——定比分点特殊化

除了可以将比例系数特殊化外,还可以将定比分点特殊化,即P为x轴或y轴与直线的交点,我们以与x轴的交点为例,设P(m,0),此时直线AB可设为(y1－y2)x＋(x2－x1)y＝x2y1－x1y2,这里给出3种不同的求解方法.

解法1因为所以A,B,P三点共线,所以交叉相乘再平方,得

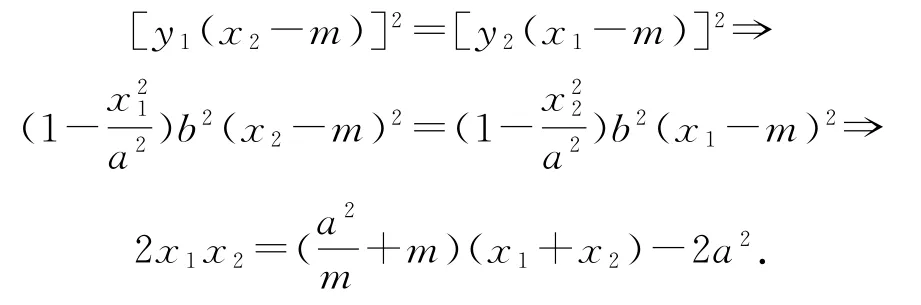
解法2令y＝0,则x2y1－x1y2＝m(y1－y2),我们去求它的对偶式x2y1＋x1y2,

接下来就可以根据

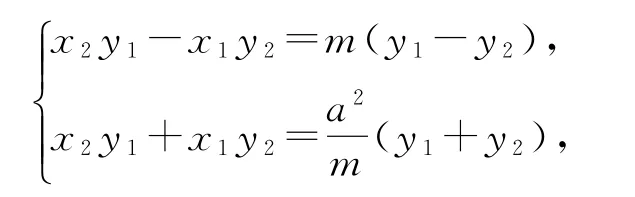
去求解x2y1,x1y2的值,利用结构关系达到消元的目的.

解法3因为,

所以

以上就是定比分点特殊化以后的3种不同的求解方式,都体现了一个减元的思想.

综上所述,在设点研究定比点差法的命题背景下,体现了两类经典问题：1)点差法的理解与应用;2)圆锥曲线中的定点、定值问题.思想层面统一体现为减元、消元思想以及方程的思想,数学核心素养层面,主要体现对数学运算及逻辑推理的培养.