某型火箭发射装置起竖臂拓扑优化设计与仿真

张 乐， 张佳兴， 肖登宝， 赵宪斌， 康文俊

（1.中国航天科技集团有限公司 第四研究院第四十一研究所， 陕西 西安 710049；2.北京理工大学 先进结构技术研究院， 北京 100081；

3.西安交通大学 机械结构强度与振动国家重点实验室， 陕西 西安 710049）

0 引言

探空火箭是在近地空间进行科学试验的火箭， 随着我国空间科学试验需求的持续旺盛， 探空火箭的发射更加频繁，技术水平也逐步提高[1-4]。探空火箭通常由发射装置发射，随着火箭的质量和尺寸的不断增加，发射装置的结构也相应的需要优化和改进[5]，从而提升发射装置的性能，减轻其质量和尺寸，有效提高机动运输能力[6]，增强经济效益。

本文以航天四院某发射装置为研究对象， 在现有成熟结构件的基础上，参考国内相关技术[6-11]，对部分部件进行布局优化和拓扑优化，轻量化改进优化设[12，13]，随后对模型的强度和模态进行有限元分析。 通过分析，优化后的起竖臂质量较小且强度满足要求， 对该部件的优化是较为成功的。 该优化方法和思路对探空火箭发射装置其它部件的优化具有借鉴意义。

1 发射装置组成

某型火箭发射装置由基座、导轨及过渡架、起竖臂、电动缸、回转驱动、发射架基座、调平系统、控制系统等组成[3]，如图1 所示。基座是整个承载平台，用来承载整个装置；回转驱动是发射装置的角位器，使发射装置按照要求进行角位旋转；起竖臂是过渡架的安装基座，是上托式发射装置定向器，用来承载过渡架；过渡架上安装有导轨，是火箭发射时的导向器； 发射装置在电动缸和回转驱动的运动下完成火箭俯仰角和方位瞄准[4]。 该发射装置基座、过渡架等结构件与新型探空火箭匹配，可以沿用，本次对起竖臂进行结构布局优化、拓扑优化与有限元仿真。

图1 发射装置组成图

2 起竖臂布局参数优化

2.1 参数优化问题描述

起竖臂上部与导轨过渡架连接； 起竖臂电动缸上支耳与电动缸连接； 起竖臂旋转轴与发射装置回转支撑连接。 三者的相对位置共同影响起竖臂整体的外部结构及型面特点。发射装置起竖臂三轴指的是起竖臂旋转轴、电动缸上支耳转轴及电动缸下支耳转轴。 三者的相对位置不同会影响发射装置的整体布局、 受力状态、 电动缸行程、电机功率等等。 为了对三轴位置关系进行优化，对问题建立数学模型，如图2 所示。

图2 发射装置组成图

根据发射装置总体指标、相关部件接口要求，初始优化条件有：①受电动缸制作要求，电动缸固定长度（不含丝杠行程部分）为1035mm，电动缸的总长为固定长度与行程之和，电动缸最小长度不小于1035mm；②受物理条件约束，电动缸零位长度加行程应大于90°起竖状态电动缸长度， 避免电动缸丝杠行程不够造成无法起竖到90°；③为有效降低电动缸电机功率，降低推力与结构重量，电动缸水平状态力臂应尽量大以减少零位状态电动缸推力（水平状态时是重力力矩最大的工况，因此主要考核水平力臂）；④为了提高起竖状态推力安全系数，电动缸起竖状态力臂不能过小；⑤电动缸起竖状态下，行程余量尽量大，防止电动缸运动过冲造成电动缸损毁；⑥电动缸行程尽量小，降低成本，提高电动缸压杆稳定性；⑦90°时电动缸的力臂尽量大以增大结构的稳定性，从而抵抗火箭发射时对发射装置的冲击力；⑧满足①～⑦条件下，电动缸上支耳与下支耳之间的垂直距离尽量小， 最大不超过1200mm，降低发射装置高度，方便其公路和铁路运输。

2.2 参数优化算法

所谓优化算法，其实就是一种搜索过程或规则，它是基于菜构思想和机制， 通过一定的途径或规则来得到满足用户的问题的解。 就优化机制与行为来分，目前工程中常用的优化算法主要可分为经典优化算法、 构造型优化算法、智能优化算法和混合型优化算法。

（1）经典优化算法。 包括线性规划、动态规划、整数规划和分技定界等运筹学中陕传统算法， 其算法计算复杂性一般很大，只适于求解小规模问题。

（2）构造型优化算法。 用构造的方法快速建立问题的解，通常算法的优化质量差别以满足工程需要。 比如，调度问题中的典型构造方法有：JohnsonM 法、Palmer 法。

（3）智能优化算法。 智能优化算法是通过模拟或揭示某些自然现象或过程发展而来的， 与普通的搜索算法一样都是一种迭代算法， 对问题的数学报述不要求满足可微性、凸性等条件，是以一组解(种群)为迭代的初始值，将问题的参数进行编码，映射为nJ 进行启发式操作的数据结构，仅用到优化的目标函数值的信息，不必用到目标函数的导数信息，搜索策略是结构化和随机化的(概率型)，其优点是：具有全局的、并行高效的优化性能，鲁棒性、通用性强等。 智能优化算法的适用范围非常广泛，特别适用大规模的并行计算。

（4）混合型算法。 指上述各算法从结构或操作上相混合而产生的各类算法。 优化算法当然还可以从别的角度进行分类，如确定性算法和不确定性算法、局部优化算法和全局优化算法，普通搜索算法与现启发式优化算法（智能优化算法）等。

2.3 相关参数优化结果

根据上述条件，根据类似的优化算法，对（1）～（7）进行公式化表达，利用Matlab 进行数值公式求解，得到三轴位置优化结果， 如表1 所示。 综合加工工艺， 选择电动缸上支耳转轴坐标（3450mm，500mm），下支耳坐标（1000mm，-500mm）。

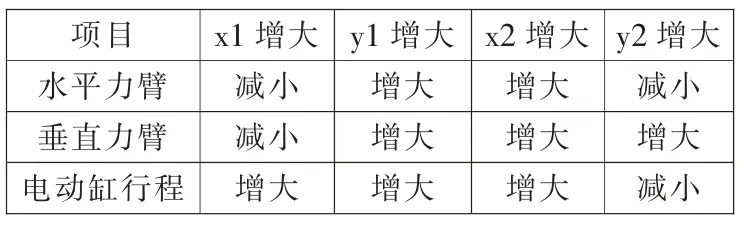
表1 三轴坐标位置变动影响关系

3 起竖臂结构拓扑优化

3.1 起竖臂初始构型

火箭发射装置起竖臂主要是配合过渡架及导轨承载火箭进行射角调节动作。 根据火箭发射要求及相关设计经验，经计算分析，导轨过渡架长度为10m，宽度0.7m，导轨及过渡架总重2300kg， 通过三块支撑板与起竖臂进行固定连接。

按照现有的导轨过渡架接口要求， 起竖臂主体部分宽度选取为700mm，高度为500mm。 起竖臂通过三块定位安装板与过渡架及导轨相连接。起竖臂约束条件，建立起竖臂三维模型，包括过渡架安装板及电动缸上支耳，初步建立起竖臂模型为7000mm×700mm×500mm 的实心结构，如图3 所示。

图3 起竖臂三维模型

3.2 起竖臂结构拓扑优化

在Ansys workbench 中对上述几何进行拓扑优化，首先进行网格划分，单元类型为六面体实体单元，赋予钢材的弹性模量200GPa，泊松比0.3。 施加8000kg 火箭及2300kg的导轨过渡架的重力负载， 这些负载通过三块过渡架安装板施加在起竖臂上。然后运用拓扑优化模块对起竖臂水平状态和竖直状态进行结构拓扑优化， 优化条件为减少90%的体积，优化后拓扑形状如图4、图5 所示。

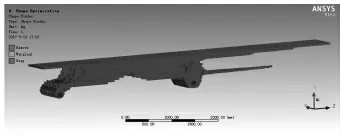
图4 水平状态拓扑优化图

图5 竖直状态拓扑优化图

3.3 起竖臂结构逆向建模

然后根据优化得到的结果，对起竖臂模型进行逆向建模，并根据工艺性等指标进行模型重构，重构所得模型如图6 所示。最后所建立的起竖臂由上支耳、后支耳及起竖臂主体结构组成，重构后的起竖臂模型质量变小，其总质量为2018kg。

图6 起竖臂内外部结构图

4 有限元仿真

4.1 结构强度仿真

对起竖臂模型进行有限元强度分析， 首先对起竖臂进行四面体实体网格划分，网格尺寸为50mm，如图7 所示。赋予模型弹性模量200GPa，泊松比0.3。对有限元模型施加8000kg 火箭及2300kg 的导轨过渡架的重力负载并进行水平工况强度计算，计算结果如图8 所示。

从计算结果可以看到，起竖臂最大应力发生在电动缸上支耳处，应力约为144.9Mpa，后支耳应力最大应力为95.5Mpa，如图7 及图8 所示。 计算结果表明，优化重构后的起竖臂模型强度满足设计要求，余量较大，对整个发射装置系统整体结构影响也较小。

图7 有限元模型图

图8 起竖臂应力云图

4.2 模态仿真

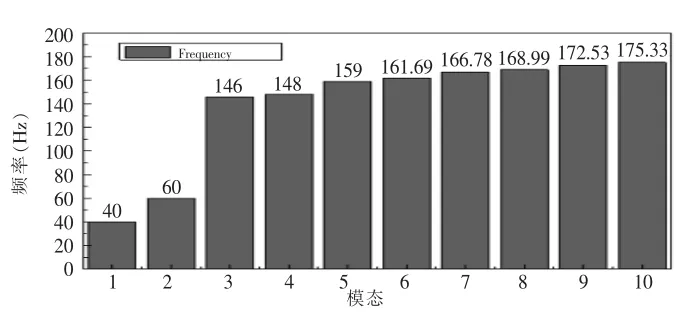
图9 起竖臂前10 阶频率图

对起竖臂进行预应力（火箭和导轨过渡架重力）下的模态分析，分析得到起竖臂的一阶和二阶频率分别为40Hz、60Hz， 可以看到起竖臂刚性较好，前10 阶频率和一二阶振型具体如图9、10 所示。

图10 起竖臂一二阶振型

5 结论

本文采用Matab对某型探空火箭发射装置起竖臂进行布局优化， 采用Ansys workbench 对与起竖臂进行拓扑优化，按照优化结果进行逆向建模，得到了起竖臂的几何模型，并采用Ansys 对起竖臂进行强度分析和模态分析， 分析结果表明该重构模型刚度好，满足设计要求。该型火箭发射装置起竖臂优化设计方法，对其它发射装置结构设计具有一定借鉴意义。