基于模糊控制的炮泥配料系统优化研究

赵燕青， 尉涛涛， 李梦佳， 刘继智， 汪 康

（1.沈阳建筑大学 机械工程学院， 辽宁 沈阳110168； 2.博众精工科技股份有限公司 研发中心事业部， 江苏 苏州215200；3.珠海泰坦新动力电子有限公司 研发中心机械部， 广东 珠海519000）

0 引言

随着钢铁产业的快速持续发展， 作为用来封堵出铁口的耐火材料的炮泥， 其需求量也是与日俱增。 一般来说， 在一次炮泥配料的过程中往往需要料车按照工艺配方要求进行大约数十次的有序运动。 在实际的控制系统中，料车运行的速度控制方面往往采用H-M-L（高速-中速-低速）模式或者H-L（高速-低速）模式，但无论采用两种模式的哪一种，都会出现速度快速变化的现象，由此将会使料车在运行中产生相应的冲击， 而影响料车的平稳运行，进而影响整个配料系统的稳定运行。 同时，为了使料车的运行的冲击不会过于严重， 在进行料车的运行频率选择时，往往不会使相邻频率水平之间差值过大，并且最高频率的选择也不会过大，因此，由于最高频率选择的受限，料车的运行速度将会受到一定的限制，进而影响配料系统的生产效率。

目前对配料系统方面的优化研究， 主要集中在称重系统及料车行走路径方面，如文献[1][2]所研究的一样，比如利用模糊神经网络改善料车动态称重性能， 利用粒子群算法、遗传算法等智能算法优化配料车行走路径等，而对于料车的运行速度及平稳性方面的研究却非常的少，但这两方面的因素对实际的生产运行效率以及设备运行平稳性的影响也是非常明显的。

综上所述，本研究将结合配料系统实际的运行情况，考虑当前的相关研究背景， 对配料车运行的平稳性与运行效率（速度）进行优化研究。

1 系统分析与建模

1.1 炮泥配料控制系统介绍与分析

炮泥配料控制系统的工艺控制过程主要包含： 上层储料罐的下料装置控制、中层料车接料行逻辑控制、下层的渡料斗与料物混碾机控制等部分， 大致情况如图1 所示的运行系统监控画面图所示。在此配料系统中，由于借料与下料的时间基本上均由原材料的性质与现场硬件装置所决定的， 混碾机的搅拌时间是由炮泥配方工艺所决定的， 而实际生产现场中料车运行轨道长达50～70m，并且设计人员对料车的运行过程的设计规划空间较大，因此，可对料车的接料运行控制进行优化，以提高配料控制系统的整体效率。

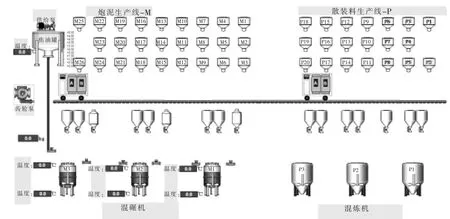
图1 运行系统监控画面图Fig.1 Diagram of operation system monitoring screen

在实际控制系统设计中， 设计人员一般采用图2（a）所示的H-M-L（高速-中速-低速）频率变化模式，根据料车与目标位置的距离S 来选用不同的频率输出值， 在此模式中，料车运行的速度和运行平稳性较为一般，根据生产现场的观察， 料车在运行过程中的频率值变化处会存在明显的冲击。 有时，为了追求更高的运行效率，也会采用图2（b）所示的H-L （高速-低速）频率变化模式，但是由于此模式下仅有两个频率变化节点， 并且在每一节点处的变化梯度增大， 料车运行的平稳性将会变得更差。

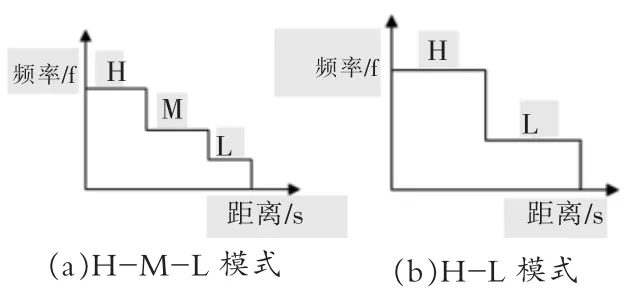
图2 两种模式下的频率变化趋势图Fig.2 Diagram of frequency change trend in two modes

1.2 系统模型的搭建与分析

根据系统的介绍与分析， 综合考虑料车的实际生产运行情况， 将料车的运行过程作为一个独立的部分进行分析，可知：运行系统根据激光测距传感器所测得的料车实时位置与所给定的料车目标位置的差值，利用S7-300 PLC 进行逻辑运算，并输出相应的电信号传送给变频器，进而控制电机的速度， 在经过行星减速器与链传动后转换为料车的运动， 由此可得出如图4 所示的运行系统控制模型。

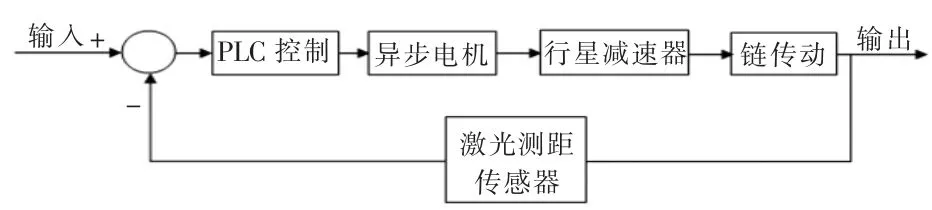
图3 料车运行系统控制模型Fig.3 Control model of feeder operation system

在运行系统的控制模型中， 异步电机的理论转速值为：

由此，结合运行系统的控制模型，可得料车运行速度ν 与频率f 之间的数学关系为：

式中：f—电机输入频率；P—电机极对数；S—转差率；n1—电机同步转速；n0—电机额定转速；d—料车轮毂直径；K1—行星减速器减速比；K2—链轮减速比。

其中的部分参数选定值如表1 所示。

根据已知条件确定料车运行系统的控制仿真模型，如图4 所示。

表1 控制模型部分参数表Tab.1 Parameter table of control model

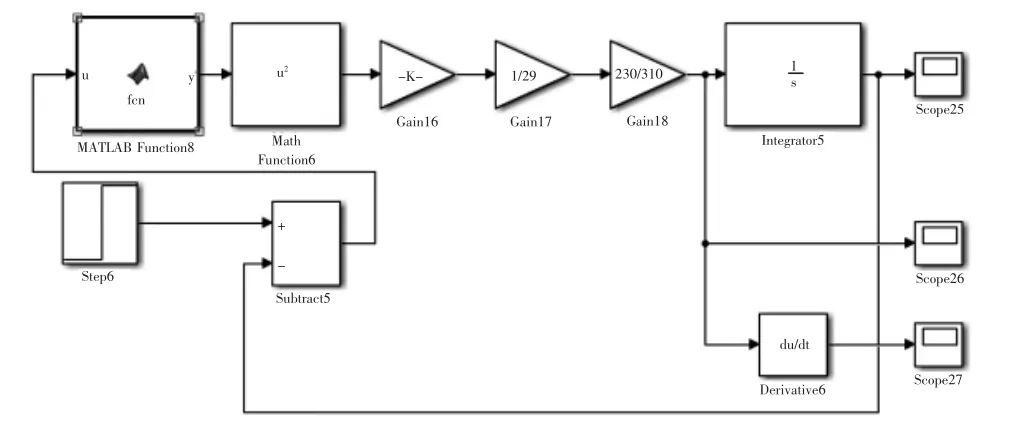
图4 料车运行系统仿真模型Fig.4 Simulation model of feeder running system

1.3 影响因素与优化策略分析

由于运行系统分析可知， 料车的运行速度v 直接影响料车的高效平稳运行，根据上述式（2）的对应关系可知，频率值f 对应运行速度v。 在图5 所示的料车接料仓结构简图中，结构框架与料车为一体，接料仓通过三个承载能力均为500kg 的重力传感器悬挂于料车上， 在下方出料口处的料车运动方向上各有一对挡板， 以减少速度变化时接料仓的摆动幅度。 同等情况下，料仓所接料的重量越大惯性也会越大， 从而料仓在速度变化时的摆动冲击也会变大，过大的冲击将会对平稳性产生较大的影响。因此，对于小车运行的平稳性来说，料车的实时接料重量也是重要影响因素之一。

由于料车在生产运行时的环境较为复杂，除料车的运行速度与实时接料量主要影响因素以外，也会有较多的外部影响因素，并且运行速度v与实时接料量m 对系统的运行效率与平稳性的影响及其评价标准难以精准的描述。因此，利用“模糊”来进行描述整个系统的运行情况及效率与平稳性的评价标准， 将会更为客观准确的呈现实际生产运行情况。

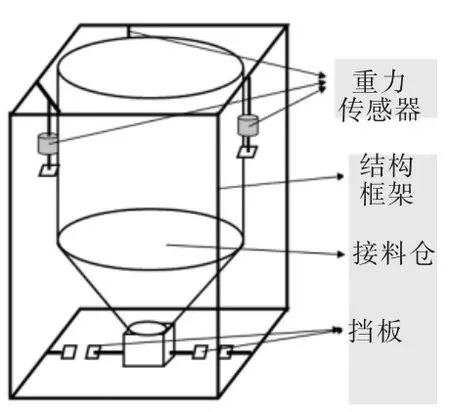
图5 料车接料仓结构简图Fig.5 Structural diagram of the material receiving bin

2 模糊控制器的设计与运用

2.1 模糊变量及其隶属函数

根据运行系统中料车高效平稳运行的主要影响因素，模糊控制器将采用两输入一输出变量，输入变量为料车实时位置与料车目标位置的差值s、料车实时的已接原材料的重量m，输出变量为变频器的频率输出值f[3-6]。

输入变量位置差值s 的模糊语言变量为S，物理论域选取为[0，4000]，模糊论域选取与物理论域相同，划分为7 个模糊子集：very near（非常近）、near（近）、medium near（中等近）、medium（中等）、medium far（中等远）、far（远）、very far（非常远），以此来涵盖模糊论域。模糊论域的划分根据实际料车运行的位置差来确定.

输入变量已接原材料的重量m 模糊语言变量为M，物理论域选取为[0，2000]，模糊论域同物理论域，划分为5 个模糊子集：very light （很轻）、light （轻）、medium （中等）、heavy（重）、very heavy（很重）。

输出变量频率值f 的模糊语言变量为F，物理论域选取为[0，50]，模糊论域同物理论域，划分为10 个模糊子集：f1 至f10，代表着频率值有非常低至非常高。

输入输出变量的隶属函数如图6 所示。

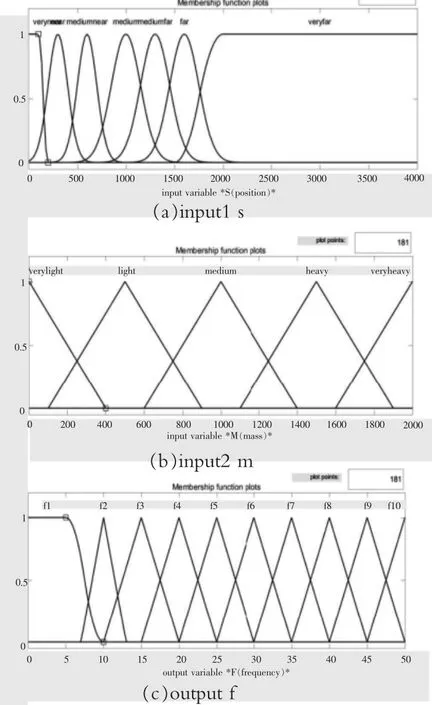
图6 输入输出变量的隶属函数图Fig.6 Membership function graph of input and output variables

2.2 模糊控制规则

配料控制系统的优化策略以提高料车的运行平稳性和运行速度为主。在料车运行的过程中，料车的运行速度是根据位置差值s 的变化而确定频率值f 所决定的，而料车运行的平稳性不仅与料车运行速度及其变化有关还与料车已接原材料的实时重量m 有关，在设计模糊规则时，将根据实际生产情况与以往经验设计s、m 与f 之间控制规则。

实际生产中由料车运行速度引起的冲击往往是由料车在较短时间或距离内速度急剧变化引起的， 因此在一定的速度下必须预留出合理的缓冲距离。当料车行驶于very far 区时，料车需要获得f10 区的频率值以拥有最高的速度来提高运行效率；当料车行驶于far 区时，料车开始进入速度缓冲距离区，获得频率值开始从f10区进入f9 区，并随着料车距离目标位置越来越小，频率值开始慢慢的向f1 区递进。由于料车运行时的平稳性亦与实时重量m 有关，并且实时重量m 越大料车拥有的惯性也就越大， 因此需要适当的降低获得的频率值，根据这一原则并结合实际运行情况与往期调试经验设计模糊规则，所设计模糊规则下的系统输入输出过程曲面图如图7 所示。

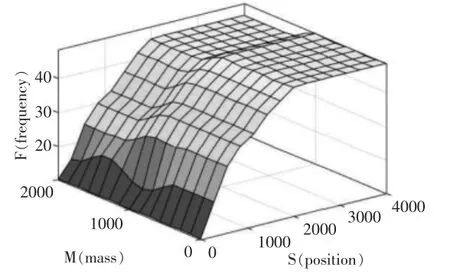
图7 系统输入输出过程曲面图Fig.7 Diagram of System input and output process surface

在原控制系统仿真模型的基础之上，根据实际运行情况，加入所设计的模糊控制器， 建立优化后的仿真控制模型如图8所示。

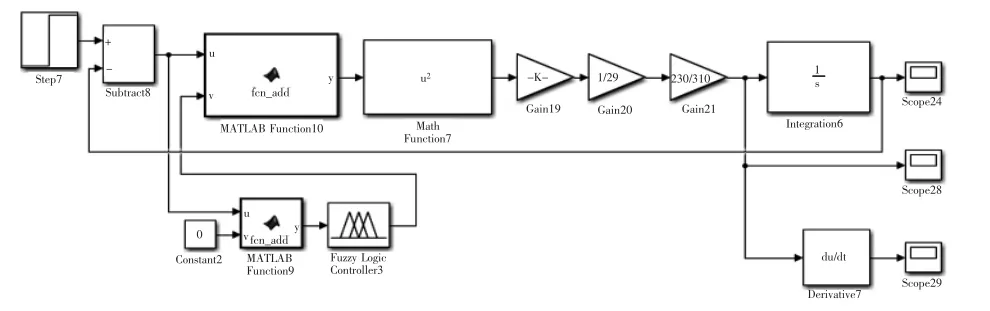
图8 优化后的料车运行系统仿真模型Fig.8 Simulation model of optimized cart operation system

3 仿真结果与分析

3.1 运行效率优化分析

利用优化后的系统仿真控制模型与原系统仿真控制模型的结合可得出便于分析的仿真结果。如图9 所示的仿真结果中，A（After）代表优化后的系统仿真控制模型在不同目标位置下的料车位移曲线，而B（Before）则代表优化前的相对部分，根据图中曲线分析可知，同等情况下，随着目标位置距离越来越大，系统优化后料车运行到目标位置所花费的时间与优化前之差越来越大，效率优化效果也就愈加的明显。

图9 料车优化前后运行曲线图Fig.9 Operation curve before and after optimization of the cart

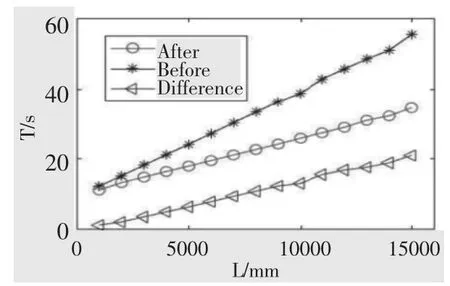
图10 料车运行时间折线图Fig.10 Line chart of cart running time

3.2 平稳性优化分析

为了较为合理评价平稳性优化情况， 可对系统优化前后的平稳性及优化后不同情况下的平稳性进行分析，而平稳性的优化效果可从速度变化趋势图及不同承载重量下料车加速度变化趋势两个方面的分析中得出。

在图11 所示的料车运行速度变化图中，同一目标位置情况下， 将900、1400、1900kg 代表的不同接料量下的速度变化与H-M-L 速度模式下相对比，可知，优化后的系统避免了速度短时间内大幅度变化的发生，其变化幅度的评价可参考如图12 所示料车优化前后的加速度变化对比图，其中B 与A 分别代表优化前后的情况，由图可知，优化后的系统避免了由于速度的突然大幅度变化而造成的大幅度冲击，从而使料车能够更加平稳的运行，提高了系统运行平稳性。

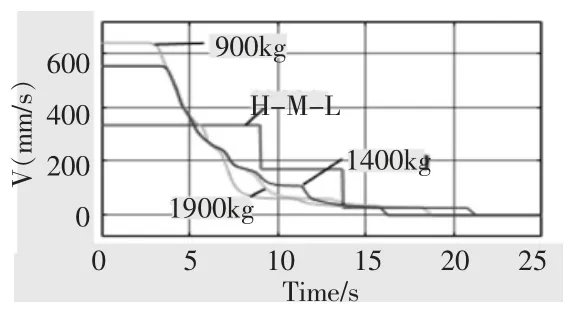
图11 料车运行速度变化图Fig.11 Change chart of runningspeed of cart

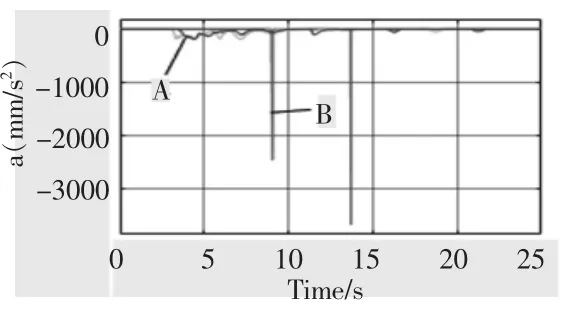
图12 优化前后料车运行加速度对比图Fig.12 Comparison chart of running acceleration before and after optimization

通过对图13 所示的优化后的料车运行加速度波动图的分析可知，料车在不同接料量下的运行加速度波动曲线基本相同，并且在整个运行过程中的整体波动情况较为平稳。 由此可得，优化后的运行系统在不同的接料状态下都可保持相似的平稳性能，并且在料车的整个运行过程中都能保持较好的平稳性。

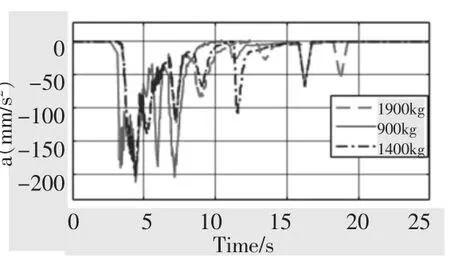
图13 优化后料车运行加速度波动图Fig.13 Fluctuation chart of running acceleration of the cart after optimization

4 结论

本文以炮泥配料控制系统为研究背景， 对实际炮泥配料系统的现场情况进行分析，并利用实际问题分析、现场调试情况以及过往经验等综合因素， 设计了基于模糊控制算法的控制器， 通过MATLAB/Simulink 将其应用于原控制系统仿真模型之上，并对仿真结果进行对比分析，验证了控制器模块设计的合理性与有效性。 此次针对炮泥配料系统的优化设计研究，具有一定的实际应用价值，并同时为其他行业相关方面的优化控制提供了思路。