DMU50V非正交五轴数控机床敏感几何误差研究

于杰 宋占群 丁爽 陈志炜

摘 要：针对DMU50V非正交五轴机床，采用多体系统理论进行机床几何误差建模，并通过Morris全局敏感性分析法识别出敏感几何误差项，分析了各误差项对机床精度的影响，辨识出敏感部件，分析结果可为机床的精密设计提供指导。

关键词：DMU50V非正交五轴机床;多体系统理论;Morris;敏感几何误差

中图分类号：TH161 文献标志码：A

复杂曲面零件在汽车工业、医疗器械、航空航天等领域得到了广泛的应用，随着各领域对产品加工质量要求的日益提高，机床结构也更加复杂多样。相比于传统的正交五轴机床，具有特殊旋转结构的非正交五轴机床在零件制造上有着特殊的优势，更加适用于复杂壳类以及回转体零件[1]的加工。与传统五轴机床相同，非正交五轴机床的加工精度同样受到几何误差，热误差，力误差等误差源的影响，其中几何误差的影响占比最大，因此识别出几何误差中的敏感项对机床加工精度的提高具有重要意义。

1 机床误差建模

识别出机床敏感几何误差项的前提为机床几何误差模型的确立。本文研究的DMU50V型非正交五轴数控机床的结构简图如图1所示，该机床包括三个平动轴（X轴、Y轴和Z轴），一个回转轴（C轴）和一个倾斜摆动轴（B轴），其中B轴轴线与主轴轴线夹角为45°。

机床的几何误差定义如下，与位置相关的几何误差如表1所示，装配误差如表2所示。

由图1的机床结构可知，机床工件链为：床身（F）-B轴-C轴-工作台;刀具链为：床身-X轴-Y轴-Z轴-刀具。根据多体系统理论对机床进行误差建模[2]，机床各轴的运动矩阵定义如下，相邻体i、j间相对静止时的理想位置变换矩阵为Mijp，其中，i（F，X，Y，Z，B，C），j（X，Y，Z，B，C）;相邻体间相对静止时的位置误差变换矩阵为ΔMijp;相邻体间相对运动时的理想运动变换矩阵为Mijs;相邻体间相对运动时的运动误差变换矩阵为ΔMijs。切削点在刀具坐标系中表示为[0 0 0 1]T，则机床的理想成形矩阵如式（1）所示，机床的实际成形矩阵如式（2）所示，式（2）减去式（1）即可得到机床的综合误差矩阵，如式（3）所示。

2 几何误差敏感性分析

Morris全局敏感性分析法[3]可以量化地表示几何误差模型中各几何误差项的变化对空间几何总误差的影响和不同几何误差项之间的耦合程度。Morris全局敏感性分析法具体形式如下：

式（4）中，EEi为第i个输入参数的影响效应，x为输入参数，y为输出函数。依次计算每个输入参数的影响效应。设定循环采样次数为SN，这样即可得到每个输入参数的SN个影响效应，分别计算每个输入参数影响效应的均值Mμj和标准差Mσj，如式（5）所示。其中，Mμj反應每个输入参数对输出函数的影响，值越大影响越大;Mσj反应每个输入参数与其他参数间的耦合强度，值越大耦合强度越高。

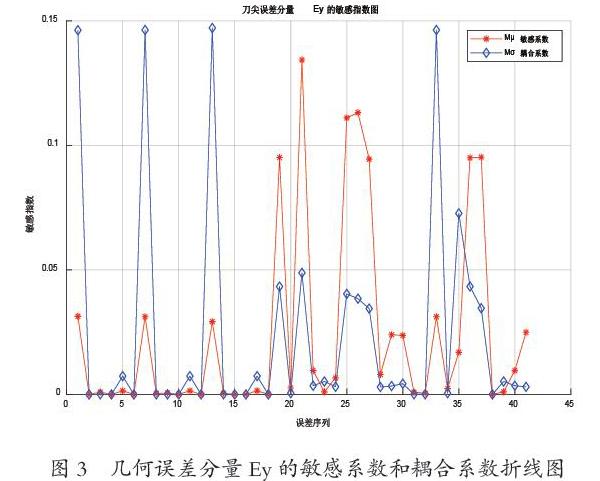
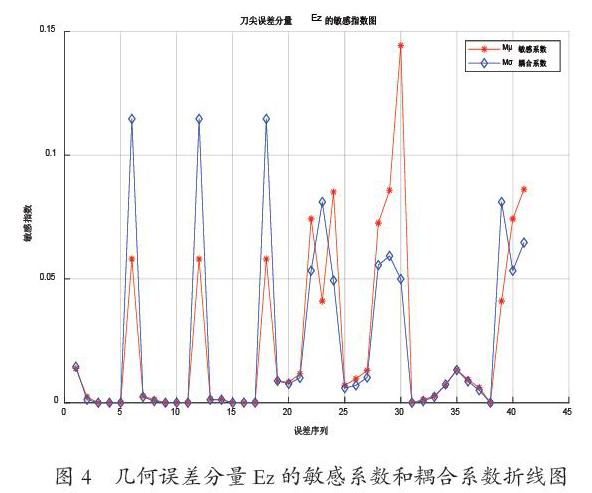
采用Morris法对机床41项几何误差进行敏感性分析，X方向、Y方向以及Z方向的几何误差敏感性指数分别如图2、图3及图4所示。其中，误差序列1-41分别为δx（X）、δy（X）、δZ（X）、εx（X）、εy（X）、εz（X）、δx（Y）、δy（Y）、δz（Y）、εx（Y）、εy（Y）、εz（Y）、μxy、δx（Z）、δy（Z）、δZ（Z）、εx（Z）、εy（Z）、εZ（Z）、μxz、μyz、δx（B）、δy（B）、δZ（B）、εx（B）、εy（B）、εZ（B）、μxb、μbz、λxb、λbz、δx（C）、δy（C）、δZ（C）、εx（C）、εy（C）、εZ（C）、μxc、μyc、λxc、λyc。这里的敏感系数和耦合系数均经过归一化处理，即该项几何误差的敏感系数（或耦合系数）占所有几何误差项的敏感系数（或耦合系数）之和的百分比。

由上述分析结果可知各误差分量受转角误差影响较位移误差影响要大得多，而B轴上的几何误差敏感系数普遍较大，这说明由于DMU50V型非正交五轴数控机床特殊的结构型式，导致其加工误差受B轴几何误差项的影响最大。

3 总结

本文针对DMU50V型非正交五轴数控机床进行分析，辨识出影响其加工精度的敏感几何误差，在机床设计阶段对产生敏感几何误差源的零部件进行精密制造，可以显著提高机床加工质量。

参考文献：

[1]Sitong Xiang， Huimin Li， et al. Geometric error identification and compensation for non-orthogonal five-axis machine tools[J]. The International Journal of Advanced Manufacturing Technology， 2018， 96（5-8）：2915-2929.

[2]刘又午. 多体动力学的休斯敦方法及其发展[J]. 中国机械工程， 2000（06）： 10-16.

[3]Morris M D. Factorial sampling plans for preliminary computational experiments [J]. Technometrics，1991，33（2）：161-174.

作者简介：

于杰（1999-），男，汉族，江苏连云港人，扬州大学，数控技术方向。

宋占群（1996-），男，汉族，黑龙江齐齐哈尔人，扬州大学，数控技术方向。

丁爽（1990-），男，汉族，江苏泰州人，数控技术方向。

陈志炜（1997-），男，汉族，山西临汾人，扬州大学，数控技术方向。