欧拉坐标系下具有锐利相界面的可压缩多介质流动数值方法研究
姚成宝 付梅艳 韩 峰 闫 凯
(西北核技术研究院,西安 710024)
(北京大学数学科学学院,北京 100871)
引言
多介质大变形问题广泛存在于军事和民用领域,例如爆炸力学效应、高速冲击问题、武器设计以及自然灾害的防护等.上述问题通常存在多种介质间强烈的相互作用,具有强耦合、大变形、高度非线性等特点,物理现象极其复杂.由于各介质之间的物理特性、初始状态差异极大,很多对单介质问题比较有效的数值方法在处理多介质问题时,通常会引起较大的数值震荡和误差[1-2],甚至导致计算无法继续,因此需要研究合适的多介质数值计算方法,准确描述不同介质间的相互作用.
多介质流动数值方法按其采用的坐标系可以分为Lagrange 方法[3]、Euler 方法[4]、ALE 方法[5-6]以及Euler-Lagrange 耦合方法[7]等.由于Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题.但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况.如何描述相界面的位置以及混合网格中各介质之间的相互作用,是Euler 方法求解多介质问题的难点.目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF(volume of fluid)方法[8-9]、MOF(moment of fluid)方法[10]、Front Tracking 方法[11-12]以及Level Set 方法[13-14]等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡.目前主要的处理方法包括两类.第一类方法是虚拟流体类方法(包括GFM[15]、MGFM[16-20]和RGFM[21-22]等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法(cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23]采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了CFL 条件对时间步长的限制.Liu 等[24]引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25]在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26-27]在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于0.5 的碎片单元,根据界面的法向确定碎片单元在x,y方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性.Meyer 等[28]在Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29]将Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于0.6 的碎片单元进行了满足守恒性质的修正处理.
本文提出了一种基于Euler 坐标系的非结构网格、具有锐利界面的二维和三维守恒型多介质流动数值方法,可用于模拟可压缩流体和弹塑性固体在极端物理条件下的大变形动力学行为.利用分片线性的Level Set 函数清晰重构出分段线性的相界面,建立了单纯形网格内具有多种介质的相界面拓扑结构,理论上可以处理全局任意种介质、局部3 种介质的多介质流动问题.提出了一种守恒型的相界面两侧介质相互作用的处理方法,能够保证不同介质间的通量守恒.提出了一种非结构网格上的单元聚合算法,通过对每个碎片单元建立至少包含一个完整单元的同介质单元片,并对该单元片内的守恒量进行基于单元体积的加权平均,扩大了碎片单元的特征尺度,消除了由于网格被相界面分割成较小碎片、违反CFL 条件,进而可能带来数值不稳定的问题.最后对激波-气泡相互作用、浅埋爆炸、空中强爆炸冲击波和典型坑道内冲击波传播问题开展了数值模拟,验证了数值方法的可靠性和计算效率.
1 物理模型
1.1 控制方程
考虑二、三维计算区域上的多介质流动问题,基于Euler 坐标系描述可压缩流体和弹塑性固体的大变形动力学行为,其控制方程组如式(1)所示

其中,ρ 表示密度,u表示速度矢量,E表示单位体积总能量,p表示压力,S表示固体的偏应力张量,对于流体S设为0,以下同.
1.2 状态方程
除了描述物质(流体或固体)的质量、动量和能量守恒的控制方程外,物质动力学行为的完整描述还需要提供描述物质自身热力学状态的本构方程(状态方程).本文涉及到的状态方程包括JWL 状态方程、理想气体状态方程以及刚性气体状态方程等.其中,JWL 状态方程用于描述TNT 爆轰产物,如式(2)所示

其中,ρ0表示初始密度,e表示质量比内能,且满足
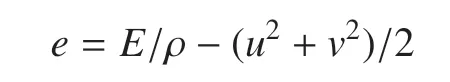
A1,B1,R1,R2,为JWL 状态方程的参数,其值分别为3.712,0.0323,4.15,0.95 和0.3.
空气采用理想气体状态方程,如式(3)所示

其中,γ 表示空气的绝热指数.
刚性气体状态方程(4)可用于描述典型的固体等在受到爆炸或冲击时的动态响应问题
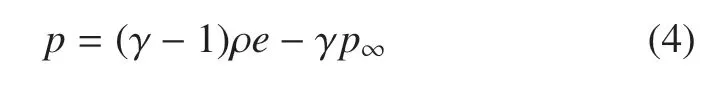
和流体不同的是,固体材料除了能够承受压缩或膨胀带来的体积变化外,还能够承受一定程度的剪切变形(形状改变).流体弹塑性模型将固体的力学响应过程分解为两个独立部分:体积变形和剪切变形,其中体积变形仍然由状态方程来确定,而剪切变形在受到强冲击或者爆炸载荷作用时可能经历3 个过程:弹性变形阶段、塑性变形阶段以及流体动力学阶段,如式(5)所示
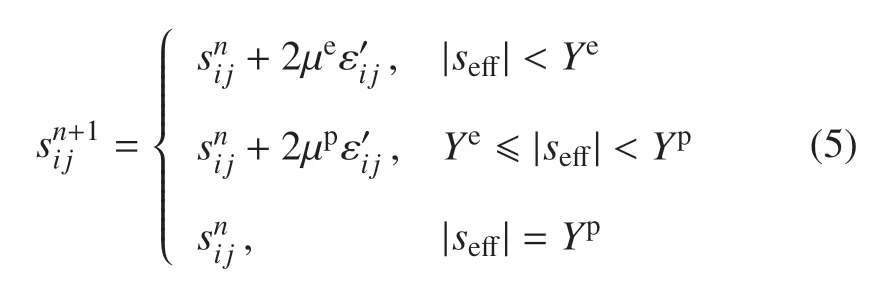
其中,sij表示偏应力分量,表示Von Mises 等效应力,表示偏应变率,µe和µp分别表示弹性和塑形剪切模量,Ye和Yp分别表示弹性和塑形屈服应力.
2 多介质流动数值方法
采用基于欧拉坐标系、具有互不相溶特征的二、三维多介质流动计算模型来进行数值离散.在任意时刻,整个计算区域Ω 可以分成两个子区域Ω+(t)和Ω−(t),且满足
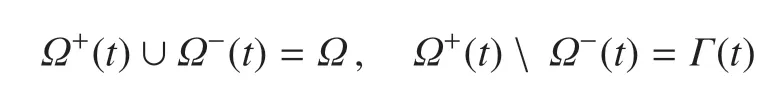
其中,Γ(t)是两种互不相溶介质之间的相界面.
利用有限体积方法求解每种介质的控制方程组,采用Level Set 方法捕捉不同介质之间的相界面,并通过在界面法向上求解局部一维多介质Riemann 问题的精确解来计算相界面上的数值通量.整个计算流程如下.
2.1 相界面追踪
Level Set 方法把随时间运动的相界面Γ(t)定义为距离函数的零等值面[30].本文利用特征线方法求解Level Set 函数的演化方程

根据特征线方法的思想,只要知道tn+1时刻网格顶点Xi上的流体在tn时刻的位置x(tn+1),就可以得到新的Level Set 函数在Xi上的值.对每个顶点Xi,利用特征线方法可得

再利用代数平均,可得新的Level Set 函数
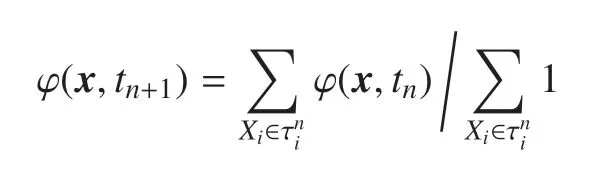
利用显式正系数格式[31]求解如下所示的重新初始化方程

2.2 相界面几何重构
当得到tn时刻的Level Set 函数后,根据其分片线性的特征重构出界面单元内分片线性的相界面,包括:二维两相、二维三相、三维两相和三维三相情形,具体如下.
2.2.1 二维两相情形
图1 给出了二维情形下单元内包含两种介质时的相界面几何结构.假设在三角形∆ABC中,顶点A;B;C处的Level Set 函数值分别为.如果某个顶点的函数值与其他两个顶点具有相反的符号,该单元一定为相界面单元,且该单元中存在两种介质.
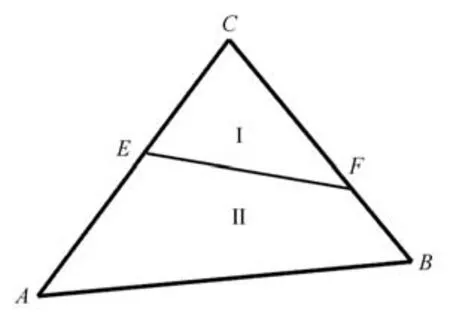
图1 二维相界面拓扑结构(两相情形)Fig.1 Two-dimensional topology of phase interface(two-phase case)
不失一般性,假设在三角形∆ABC中,C点的相编号为I,A,B两点的相编号为II,且存在相界面EF.根据水平集函数分片线性的特征,可计算E;F的坐标
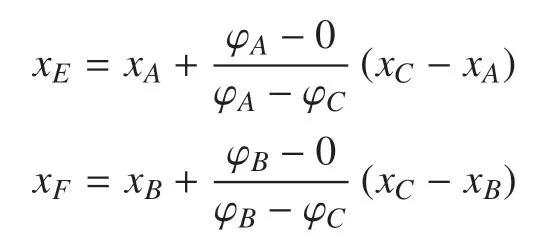
且第I 相、第II 相所占的面积分别为

2.2.2 二维三相情形
采用向量型水平集函数来描述超过两相情形时的相界面.对任一点x,向量型水平集函数在该点的取值为,如果其最大分量为,则该点的相编号为i.其中,n表示相数.
如果三角形ABC中3 个顶点的相编号各不相同,该单元中存在3 种介质,如图2 所示.不失一般性,假设A;B;C三点的相编号分别为I,II,III.根据水平集函数的分片线性特征,可得单元3 条边上的相界面分界点D;E;F的位置
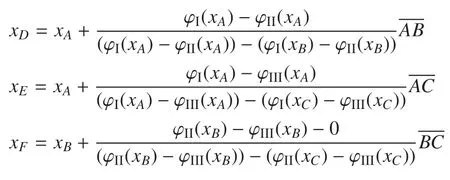

图2 二维相界面拓扑结构(两相情形)Fig.2 Two-dimensional topology of phase interface(three-phase case)
下面确定三相分界点G,记

采用如下近似
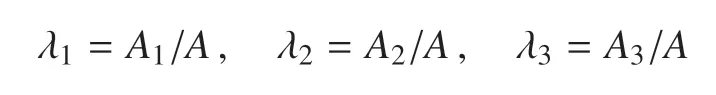
来确定三相分界点的位置,然后计算各相所占的面积和两两之间的相界面.其中G的位置为
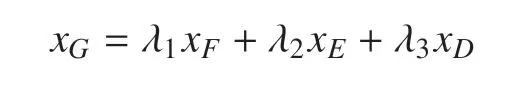
此时,第I 相所占的面积为A∆ADE+A∆DEG,第II 相所占的面积为A∆BDF+A∆DFG,第III 相所占的面积为A∆CEF+A∆EFG.I,II 两相的相界面为线段DG,I,III 两相的相界面为线段EG,II,III 两相的相界面为线段FG.
2.2.3 三维两相情形
根据水平集函数与三维四面体网格的相交情况,可以将三维两相的相界面几何结构分为两种情形,分别如图3(a)和图3(b)所示.

图3 三维相界面拓扑结构(两相情形)Fig.3 Three-dimensional topology of phase interface(two-phase case)
(1)情形1
四面体ABCD中有一个顶点与其他3 个顶点的相编号不一样,不妨设A点的相编号为I,B,C,D三点的相编号为II(如图3(a)所示),此时
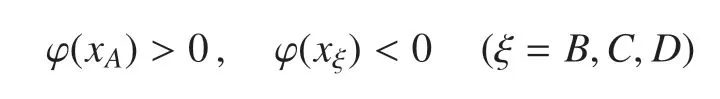
根据水平集函数的分片线性特征,使用和二维两相情形类似的算法可得四面体棱上的相分界点E,F,G,此时相界面为∆EFG,且第I 相所占的体积为
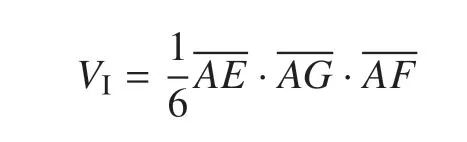
第II 相所占的体积为

(2)情形2
四面体中4 个顶点按相编号平均分为两组.不妨设A,B的相编号为I,C,D的相编号为II,如图3(b)所示.使用和情形1 类似的算法,可以计算出四面体棱上的相分界点E,F,G,H,此时相界面为四边形EFGH.记
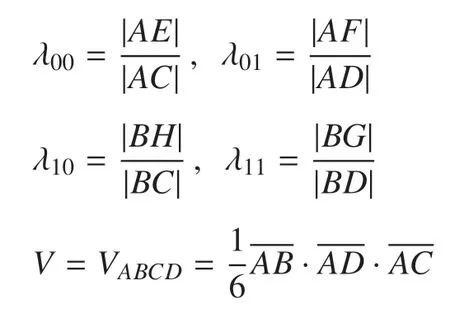
则II 相所占的体积为

I 相所占的体积为

2.2.4 三维三相情形
图4 给出了三维情形下单元内包含3 种介质时的相界面拓扑结构.根据水平集函数的分片线性性质,四面体网格的四个顶点中必然有两个为一相,另外两个顶点各占据一相.不失一般性,不妨设A的相编号为I,B的相编号为II,C,D的相编号为III.
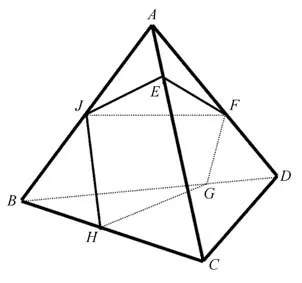
图4 三维相界面拓扑结构(三相情形)Fig.4 Three-dimensional topology of phase interface(three-phase case)
使用和前面类似的算法,可以计算出四面体棱上的相分界点,包括:相I 与相III 的分界点E,F,相II 与相III 的分界点G,H,以及相I 与相II 的分界点K,此时四面体单元ABCD内包含两个相界面:三角形EFK和四边形FGHK.整个四面体单元的体积为
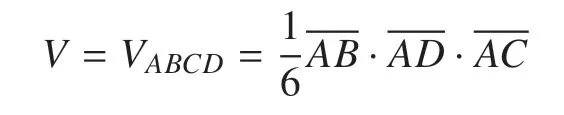
I 相所占的体积为

II 相所占的体积为

III 相所占的体积为

2.3 数值通量
在Euler 坐标系下的多介质数值计算中,每个单元内守恒量的变化来自两个部分:(1)单元内介质与单元外同相的介质在单元边界上通过流入流出或相互作用力而带来的守恒量变化,称为单元边界通量;(2)不同相的介质在相界面处由于相互作用力带来的守恒量变化,称为相界面通量.
以二维两相情形为例(如图5 所示),假设单元Ki;n与单元Kj;n具有共边Sij;n,且包含物质界 面将Ki;n和Sij;n依次分为2 个部分,此时单元包含2 种介质,每种介质的守恒量分别定义为


图5 多介质流动计算模型示意图Fig.5 Schematic diagram for the multi-media flow calculation model
(1)单元边界数值通量
单元边界的数值通量是指单元边界上同种介质之间的数值通量,且满足

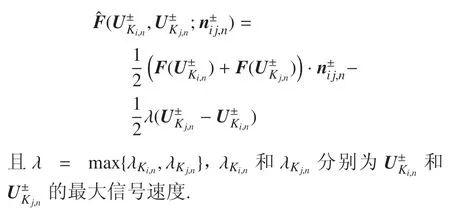
(2)相界面数值通量
相界面数值通量是相界面两侧不同介质之间的数值通量,且满足
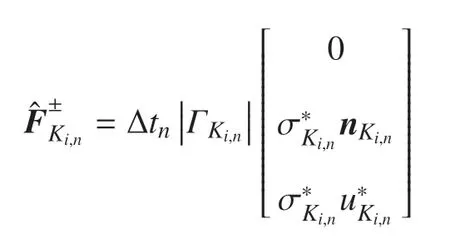
2.4 守恒量更新
当计算得到Ki;n的单元边界数值通量和相界面数值通量后,可对该单元中每种介质的守恒量进行如下更新
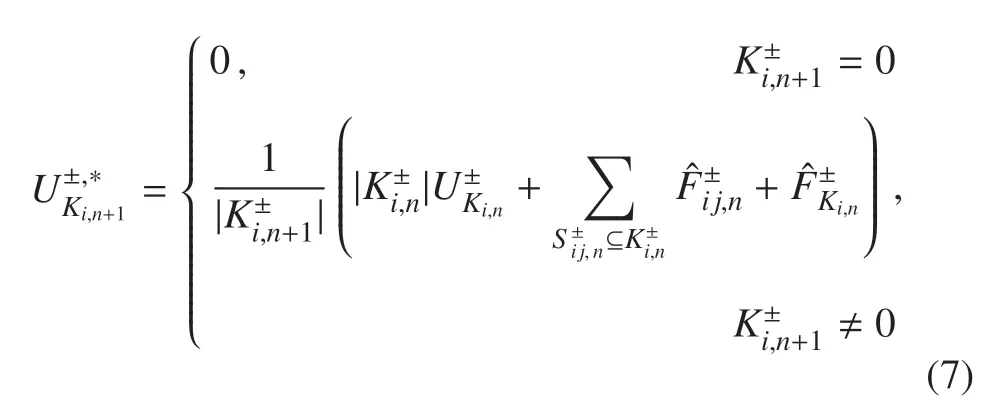
2.5 单元碎片聚合
利用式(7)来更新守恒量,等价于在原始背景网格Λ 和相界面耦合的网格上求解控制方程组.由于有些网格单元被相界面分割成一些碎片,这些碎片单元的尺寸比原始单元的尺寸小,导致CFL 条件被破坏,可能造成数值不稳定.为了消除不稳定性,需要对进行特殊处理.首先建立单元片,使得每个碎片单元都处于同介质的单元片中,并且该单元片中至少包含一个完整单元;然后修正守恒量,对单元片中每个单元上的介质守恒量进行单元体积的加权平均,以保证整体物理量的守恒.图6 为网格聚合算法及碎片处理的示意图.

图6 网格聚合算法及碎片处理Fig.6 Cell aggregation and fragment process
2.5.1 建立单元片
提出如下的聚合算法来建立单元片.首先把包含碎片的单元(即界面单元)收集起来
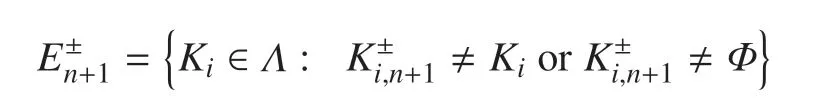
再把与界面单元相邻并且只含有当前所考虑介质的单元收集起来,作为种子单元

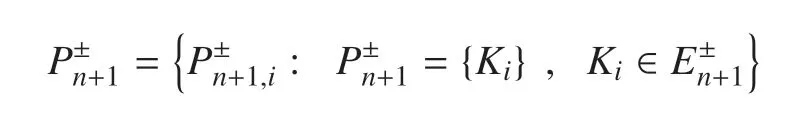
具体算法流程如下:
2.5.2 修正守恒量
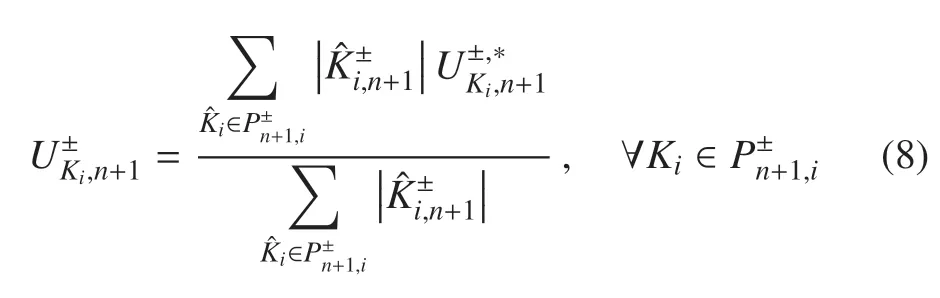
可以证明,后处理方法(8)满足
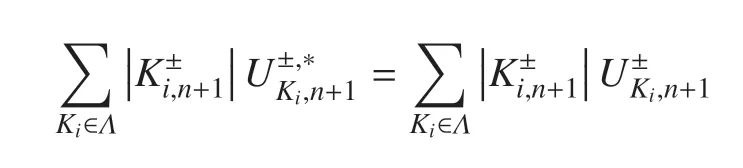
后处理过程(8)实际上消去了同一单元片内部单元间的数值通量,将过程(7)的更新改为只考虑单元片边界上的通量.由于每个单元片中至少有一个完整单元,因而满足CFL 条件,整个算法的数值稳定性得到了保证.
如果一个小的单元碎片孤立存在于其他介质单元中,有可能整个单元片中没有一个完整的单元与它含有相同的介质.因此,有些在算法完成之后只有一个单元,将这些单元合起来作为一个单元片,称之为“孤岛”.如果孤岛的体积小于预设的忍量(原始单元体积的10−8),直接将孤岛上该介质的守恒量设为缺省的极低压状态,计算过程中孤岛会逐渐缩小直至消失,这种做法可以有效地消除过于复杂的相界面,因此总的计算量得到控制.
3 数值算例
本节给出一些数值算例来对数值方法进行测试,包括多介质Riemann 问题、激波与气泡相互作用、触地浅埋爆炸以及典型坑道内的冲击波传播等问题,验证数值方法的可靠性和计算效率.
3.1 多介质Riemann 问题
首先计算一个JWL 状态方程的单介质Riemann问题,来自文献[34].计算区域为[0,1]×[0,5.0×10−3],网格尺寸为2.5×10−3.其中,JWL 状态方程参数取A1=854:5 GPa,A2=20:5 GPa,=0:25,R1=4:6,R2=1:35,ρ0=1840 kg/m3.初值条件如下

计算时间为t=1:2×10−5.计算结果与文献[34]参考解的对比如图7 所示,对比表明本文结果与文献中的高精度参考解符合较好,且在相界面处密度具有高分辨率.
再计算一个JWL--弹性固体的Riemann 问题,其中气体相用JWL状态方程来描述,参数为A1=854:5 GPa,A2=20:50 GPa,=0:25,R1=4:6,R2=1:35,ρ0=1840 kg/m3.固体相的静水压力用刚性气体状态方程描述,且γ=4:4,=600 MPa,固体的偏应力遵守Hooke 定律,且βe=1014Pa·kg/m3[35].初值条件如下


图7 Shyue 激波管问题Fig.7 Shyue shock tube problem
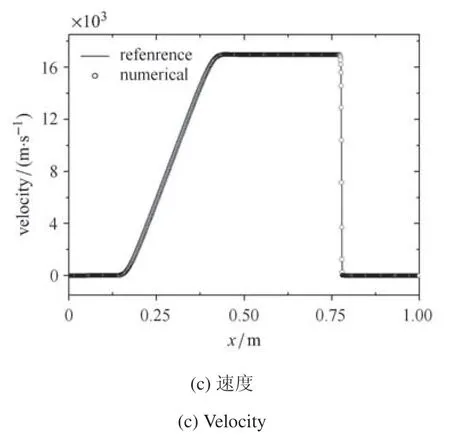
图7 Shyue 激波管问题(续)Fig.7 Shyue shock tube problem(continued)
计算时间为t=10−4.图8 给出了计算结果与参考解[35]的对比,从对比分析可知数值结果与参考解符合较好,且在接触间断和激波附近具有较高的分辨率.
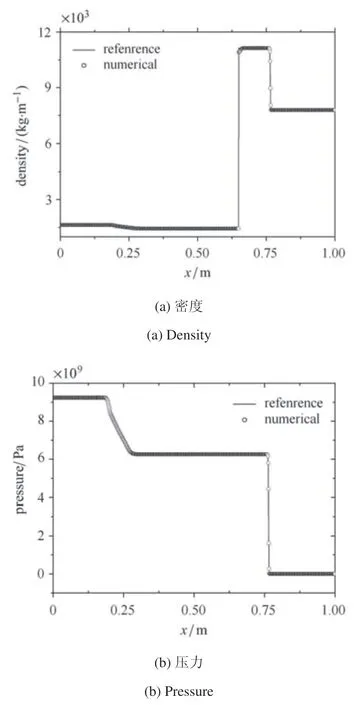

图8 JWL-弹性固体Riemann 问题Fig.8 JWL-elastic solid Riemann problem
3.2 激波与气泡相互作用
激波与气泡作用问题是可压缩多介质流体问题的一个经典算例[36-38].初值条件如下:一个直径为50 mm 的圆形气泡放置在长311.5 mm、宽89 mm 的激波管的正中间,其余地方充满空气(如图9 所示).初始时刻,气泡右侧5 mm 处有一个马赫数为Ma=1:22、向左运动的平面激波.初始物理参数如表2 所示.计算模型的上、下边界设为反射边界条件,左、右边界设为出流边界条件,网格尺寸为1 mm.

图9 激波与气泡相互作用问题示意图Fig.9 Computational model of gas-bubble interaction problem
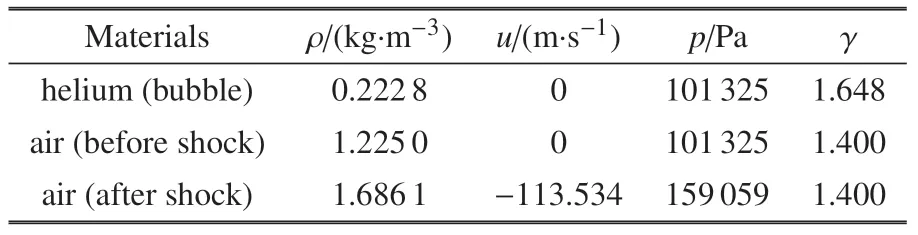
表2 激波与气泡问题的初始物理参数Table 2 Initial physical parameters of gas-bubble problem
图10 给出了不同时刻的数值结果,并与Haas 和Sturtevant 的实验结果[38]进行了比较.图中第一列为实验纹影图,第二列为数值计算得到的密度等值线图.
从图10 可以看出,数值计算结果与实验结果定性吻合.当激波从密度大的空气进入密度小的氦气时,气泡的上游边缘呈现出Richtmyer-Meshkov 不稳定性,其蘑菇形状在445µs 时刻发生.从427µs 开始气泡发生严重变形,到674µs 时空气的上尖峰和下尖峰形成.随后气泡变得越来越薄,直至发生破裂.算例中的气泡大变形问题对数值计算提出了很大的挑战,但计算结果表明,本文的数值方法可以很好的追踪相界面,同时能够保持y方向上解的对称性,证明了数值方法的正确性.
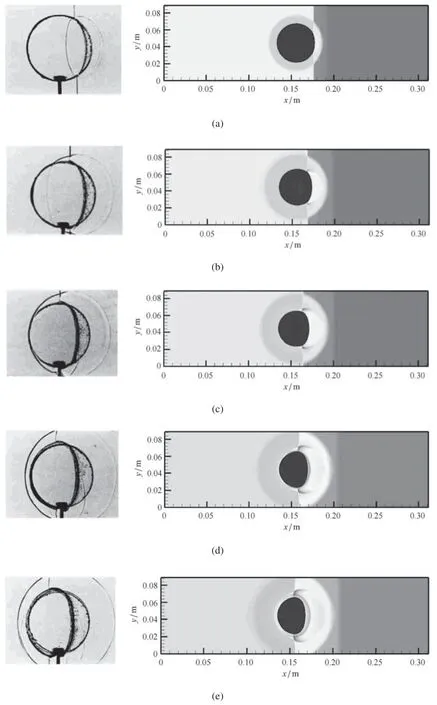
图10 激波与气泡相互作用问题.第一列从上到下依次为32µs,53µs,62µs,72µs,82µs,102µs,245µs,427µs,674µs和983µs;第二列从上到下依次为23µs,43µs,53µs,66µs,75µs,102µs,260µs,445µs,674µs和983µsFig.10 Gas-bubble interaction problem.First column:32µs,53µs,62µs,72µs,82µs,102µs,245µs,427µs,674µs and 983µs;Second column:23µs,43µs,53µs,66µs,75µs,102µs,260µs,445µs,674µs and 983µs

图10 激波与气泡相互作用问题.第一列从上到下依次为32µs,53µs,62µs,72µs,82µs,102µs,245µs,427µs,674µs和983µs;第二列从上到下依次为23µs,43µs,53µs,66µs,75µs,102µs,260µs,445µs,674µs和983µs(续)Fig.10 Gas-bubble interaction problem.First column:32µs,53µs,62µs,72µs,82µs,102µs,245µs,427µs,674µs and 983µs;Second column:23µs,43µs,53µs,66µs,75µs,102µs,260µs,445µs,674µs and 983µs(continued)
3.3 浅埋爆炸问题
计算一个二维三相问题--浅埋爆炸,用于测试本文方法在处理三相问题时的能力.计算区域内包含3 种介质:爆炸产物、空气和地介质.爆炸产物初始半径为0.1 m,初始时刻位于地下0.1 m 处.爆炸产物和空气采用理想气体状态方程,绝热指数均为1.4.地介质的静水压力部分采用刚性气体状态方程,偏应力部分采用理想弹塑性材料模型,且γ=4:4,=6 kPa,µe=853 kPa,µp=0,Ye=6:5 kPa.初值条件如下
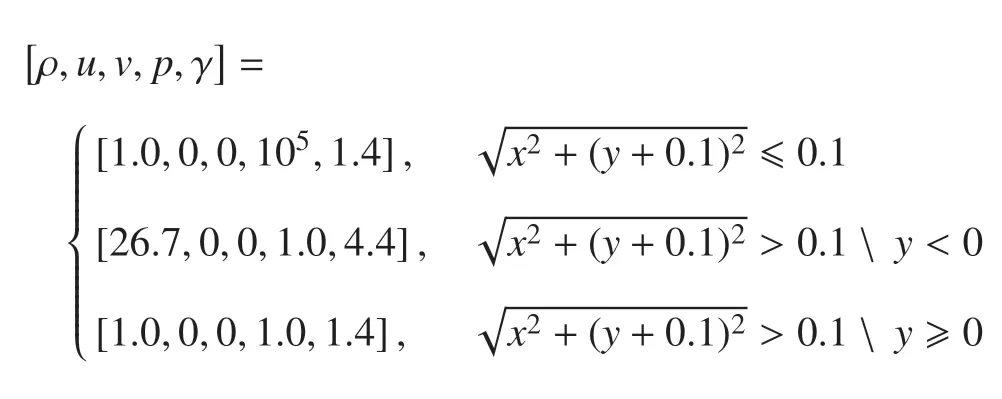
图11 和图12 分别给出了浅埋爆炸条件下,典型时刻整个计算区域内的密度和压力分布情况.在浅埋爆炸问题中,炸药爆炸产生的冲击波会剧烈压缩地介质,并在地介质中形成应力波.当冲击波突破地表面后,形成弹坑,并喷射到空气中形成强冲击波.从计算结果来看,本文的数值方法能够正确反映浅埋爆炸时的实际物理过程,表明本文的三相数值方法是正确的.
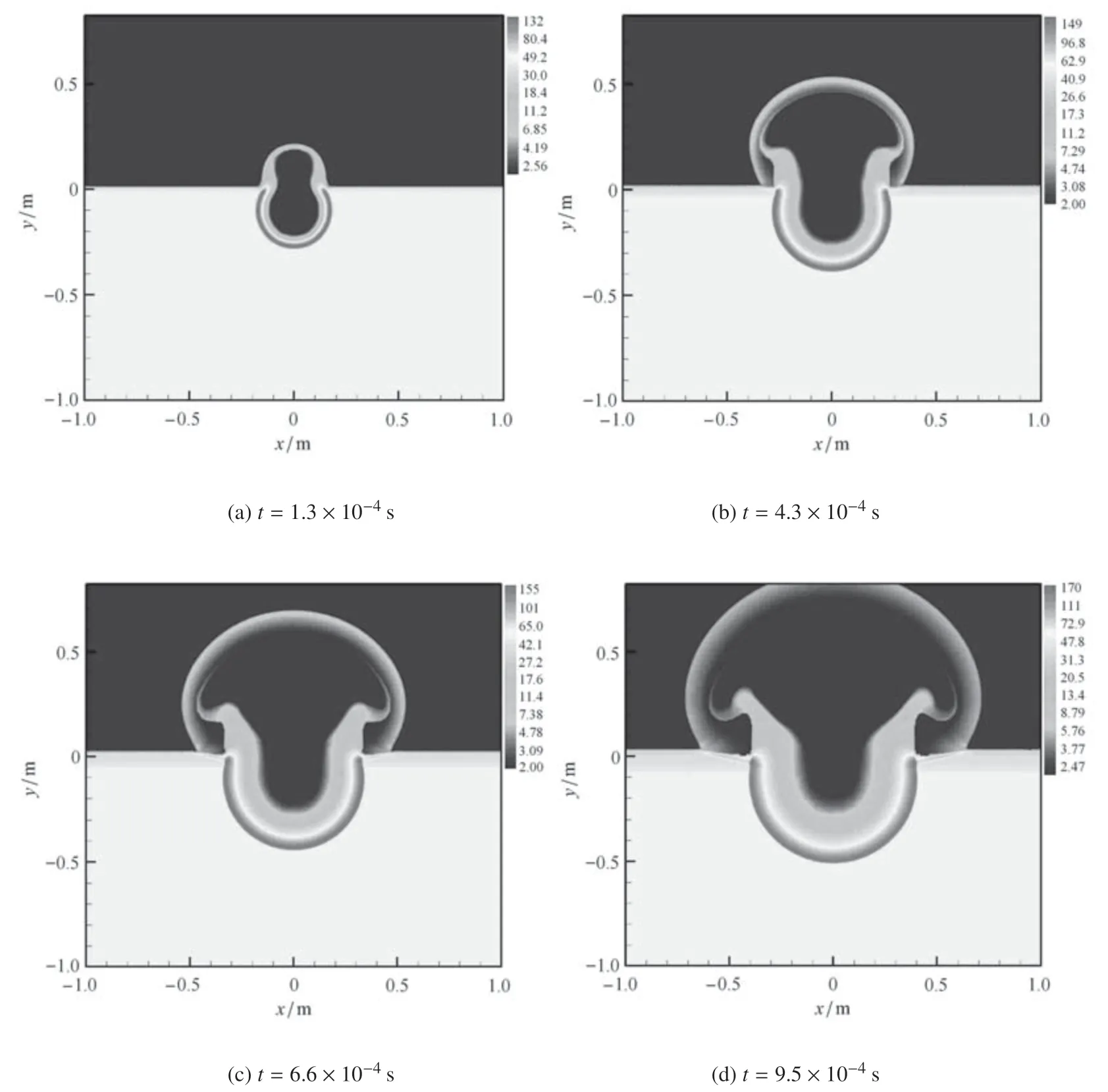
图11 浅埋爆炸典型时刻的密度云图Fig.11 Density contours of sub-surface blast problem
3.4 空中强爆炸冲击波传播
计算一个当量为1 kt TNT、爆高为200 m 的空中强爆炸冲击波传播问题.强爆炸产物采用等温等压球模型,取爆炸总当量的85%作为强爆炸的力学初始能量[39].空气采用理想气体状态方程,初始压力为101.3 kPa,初始密度为1.29 kg/m3.计算区域在x=0 和y=0 设为固壁反射边界条件,其余边界设为无反射边界条件.
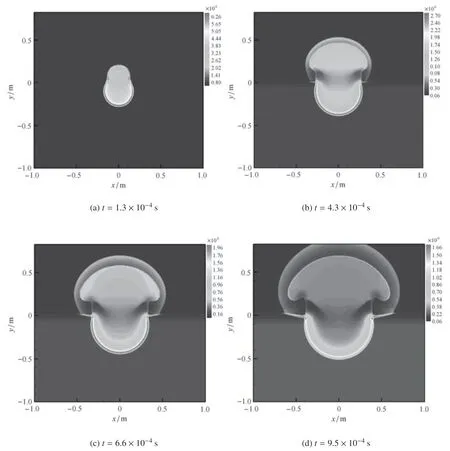
图12 浅埋爆炸典型时刻的压力云图Fig.12 Pressure contours of sub-surface blast problem
计算得到典型时刻的冲击波压力等值线如图13 所示,当空中强爆炸产生的冲击波传播到地面时,最早在爆心投影点发生正反射,然后以逐渐增大的入射角发生斜反射,产生双激波结构的规则反射(图13(a)).随着冲击波向外继续传播,入射角不断增大.当入射角增大到临界角附近时将发生马赫反射,此时反射波阵面和入射波阵面的交点离开地面,形成垂直于地面的马赫杆(图13(b)).随着冲击波的进一步传播,马赫杆不断增长.
图14 给出了数值计算得到的地面冲击波载荷分布(峰值超压和冲量)与实测结果拟合的经验公式[40]的对比情况.由对比可知,计算得到的地面冲击波参数与实测结果符合得较好,最大误差不超过40%.

图13 空中强爆炸典型时刻的压力云图Fig.13 Pressure contours of air blast at typical time
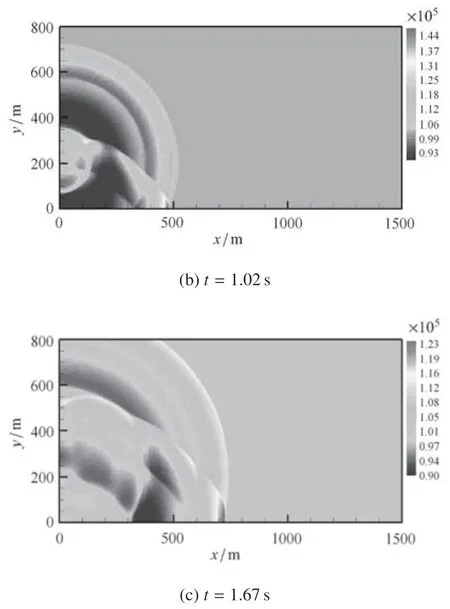
图13 空中强爆炸典型时刻的压力云图(续)Fig.13 Pressure contours of air blast at typical time(continued)
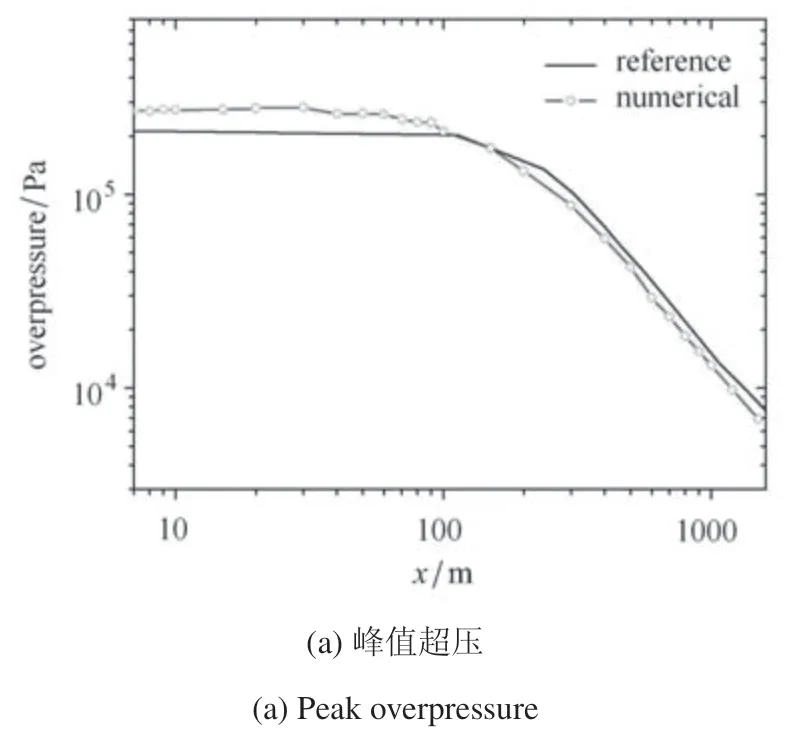
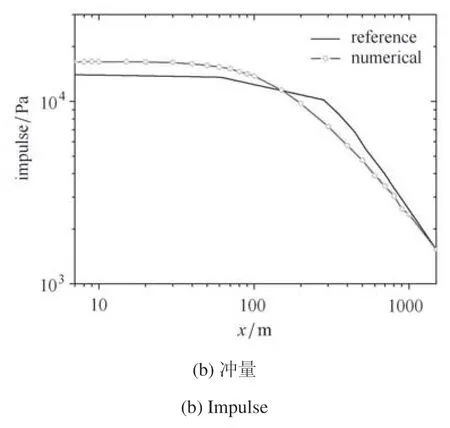
图14 地面不同距离处的冲击波参数Fig.14 Blast wave parameters on the ground at different radii
3.5 三维坑道中冲击波传播
计算了1 kg TNT 爆炸产生的冲击波在一个“十”字形三维密闭空间中的传播过程.考虑空间结构的对称性,将其简化为一个“L”型的结构.其中,E1=[0;2]×[0;2]×[0;6]m,E2=[0;6]×[0;2]×[0;2]m.TNT 和空气分别采用JWL状态方程和理想气体状态方程来描述.由于三维的计算量很大,本文采用了网格自适应技术并结合基于区域分解的并行计算策略,有效提高了计算效率.图15 给出了典型时刻的冲击波流场压力云图,图16 给出了t=9:2×10−4s时刻典型位置处的冲击波压力切面图.计算结果表明,TNT 爆炸后将在空气中产生强冲击波,起初波阵面以球面波的形式向外传播.当冲击波遇到固壁时,将发生反射并沿壁面继续向前传播,最终在整个密闭空间中形成非常复杂的载荷分布.
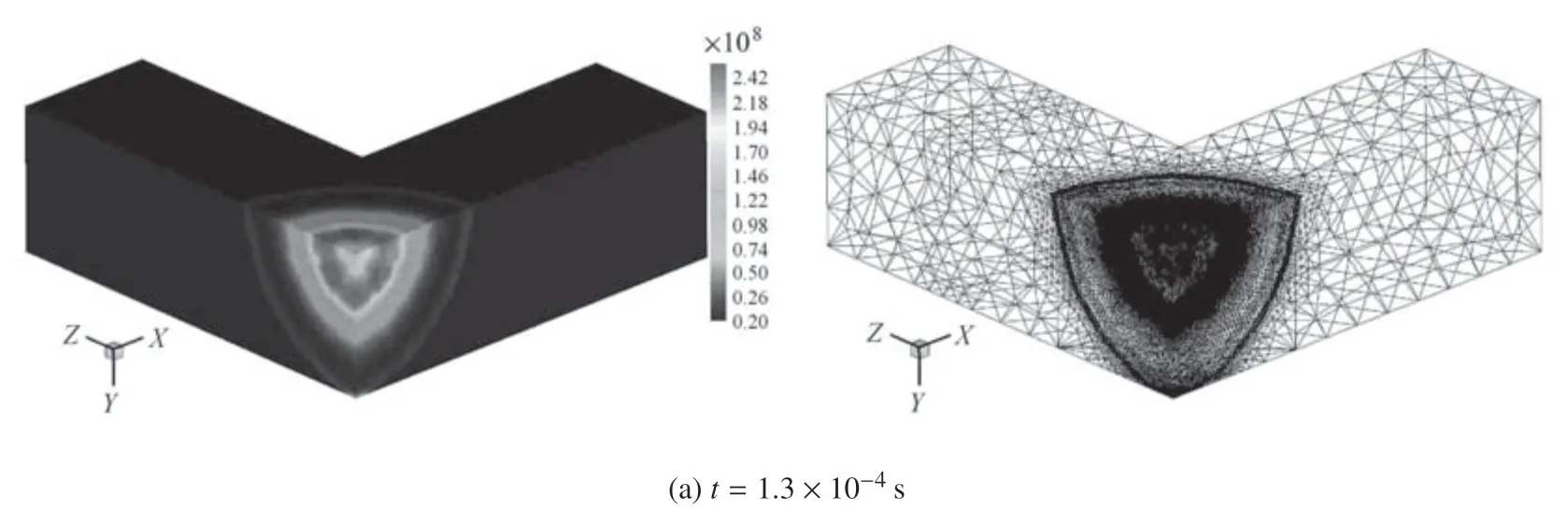
图15 典型时刻的三维冲击波压力云图和网格自适应图Fig.15 Pressure contours and adaptive meshes of three-dimensional blast wave propagation
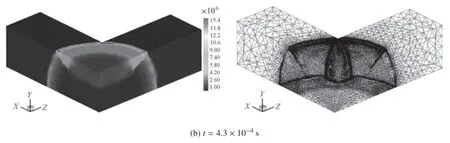
图15 典型时刻的三维冲击波压力云图和网格自适应图(续)Fig.15 Pressure contours and adaptive meshes of three-dimensional blast wave propagation(continued)

图16 t=9:2×10−4 s 时的冲击波压力切面图Fig.16 Typical pressure sections of blast wave at t=9:2×10−4 s
4 结论
本文提出了一种基于Euler 坐标系的非结构网格上互不相溶的、具有锐利相界面的守恒型多介质流动数值方法,建立了二维和三维单纯形网格上的多介质流动数值模拟程序,可用于模拟可压缩流体和弹塑性固体在爆炸与冲击等极端物理条件下的大变形动力学行为.本文提出的多介质流动数值方法采用了向量型的水平集函数,理论上可以处理全局任意种介质、局部三种介质的多介质流动问题,且能够保持锐利的相界面.此外,提出的基于非结构网格上的聚合算法能够从本质上消除由于网格被相界面分割成较小碎片而带来的数值不稳定性,有效提高了数值计算的效率和健壮性.最后结合具有代表性的数值算例和实际应用问题,验证了数值方法在处理多介质大变形和相界面大变形问题中的能力.

