基于方差分解的堆芯下封头熔池模型敏感性分析

李治刚，安 萍，明平洲，潘俊杰，芦 韡,*，余红星

(1.中国核动力研究设计院，四川 成都 610041；2.核反应堆系统设计技术重点实验室，四川 成都 610041)

在发生堆芯熔化的严重事故中，堆芯熔融物可能会迁移至压力容器下封头，严重威胁压力容器的完整性[1-2]。熔融物堆内滞留(IVR)是一项重要的严重事故缓解措施，已应用于华龙一号和AP1000等[3]三代堆中。熔池熔融物的分布及流动换热特性决定了压力容器壁面热流密度的分布，直接影响IVR的有效性。Theofanous等[4]在AP600的IVR分析报告中提出了氧化物层和金属层的两层熔池模型。近年来，Parker等[5]发现二氧化铀、二氧化锆与金属锆在高温熔池内会发生复杂的化学反应，形成以铀为主要成分的重金属层，提出了三层熔池模型。

采用集总参数法的下封头熔池模型在工程上广泛用于堆腔注水冷却系统(cavity injection and cooling system, CIS)有效性的评价，该模型基于熔池分层结构及材料成分，采用衰变热内热源驱动的自然对流计算得到压力容器下封头的表面热流密度、压力容器壁厚、氧化壳厚度等参数，实现对压力容器下封头完整性的评价，并为严重事故缓解策略的制定提供参考。由于熔池形成过程涉及大量的质量交换、能量传递，使下封头熔池模型具有关系式复杂、输入参数多且具有很大不确定性的特点，分析输入因素对下封头有效性的影响程度有助于下封头熔池模型严重事故缓解策略制定的优化。

传统的局部敏感性分析方法在应用于复杂模型的敏感性分析时具有效率低、计算量大的缺点，本文采用中国核动力研究设计院自主研发的基于方差分解的全局敏感性分析工具SALib(sensitivity analysis library)和下封头冷却剂注入系统(coolant inject system, CIS)有效性评价程序CISER对下封头熔池模型进行输入参数敏感性分析，系统介绍方差分解法和下封头熔池模型的基本理论，并对敏感性分析工具SALib进行初步验证，针对下封头熔池模型开展AP1000重要结果的敏感性分析。

1 理论模型

1.1 方差分解法

敏感性分析是一种定量描述模型输入参数对输出结果的重要性程度的方法，包括局部敏感性分析方法和全局敏感性分析方法。局部敏感性分析只检验单个参数对模型的影响程度；而全局敏感性分析[6]可同时考虑多个参数对模型输出的影响，并分析各参数之间的相互作用对模型输出的影响，广大研究者对该方法开展了深入的研究和推广，提出了如方差分解法、神经网络法、PaD2方法、FAST方法等。

方差分解法是一种典型的全局敏感性分析方法，由数学家Sobol[7]提出，其核心是把模型分解为单个属性及属性之间相互组合的函数。

假设模型为y=f(x)，其中x=(x1,x2,…,xn)，xi服从[0，1]均匀分布，且f2(x)可积，模型可分解为：

(1)

其中，f0为常数，且每个分解项fi1…is(xi1,…,xis)满足：

1≤s≤n

(2)

将其称为对f(X)的分解，并且分解是唯一的。

则模型总的方差也可分解为单个参数和每个参数相互组合的影响：

(3)

将式(3)归一化，并设：

Si1,…,in=Di1,…,in/D

(4)

(5)

(6)

显然D和Di1…is分别是f(x)和fi1…is(xi1,…,xis)的方差。

根据式(1)，可获得模型单个参数及参数之间相互作用的敏感度S。

(7)

式中：Si称为1次敏感度；Sij称为2次敏感度，依次类推，S1,2,…,n为n次敏感度，共有2n-1项，敏感度即方差分解法计算的敏感性系数。参数xi总敏感度定义为：

STj=∑Si

(8)

它表示所有包含参数xi的敏感度。1次敏感度Si体现了单个输入参数的不确定性对输出参数方差的贡献程度，全部敏感度体现了单个输入参数不确定度以及该参数与其他参数的相互作用对输出参数方差的贡献程度。

近年来Saltelli等[8]对Sobol方法中敏感度的计算进行了优化，如式(9)和(10)所示，使得该方法计算效率高、易编程实现。

Si=Vxi(Ex～i(Y|xi))/V(Y)

(9)

STi=Ex～i(Vxi(Y|x～i))/V(Y)

(10)

具体的步骤如下：

1) 生成N×2D的样本矩阵，该步骤可采用抽样方法或Sobol sequence[9]生成；

2) 将矩阵的前D列设置为矩阵A，后D列设置为矩阵B；

3) 构造N×D的矩阵ABi(i=1,2,…,D)，即用矩阵B中的第i列替换矩阵A的第i列；

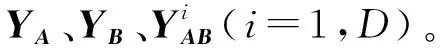
计算1次敏感度Si和总体敏感度STi，Saltelli等[10-11]的计算公式列于表1。

表1 敏感度计算公式Table 1 Sensitivity calculation formula

基于方差分解敏感性分析方法的基本理论及Saltelli等的优化工作，中国核动力研究设计院开发了具有通用性的敏感性分析工具SALib，SALib的计算流程如图1所示。

图1 SALib程序计算流程图Fig.1 Calculation flow chart of SALib code

1.2 下封头熔池模型

3层熔池结构[12-14]的传热模型如图2所示。

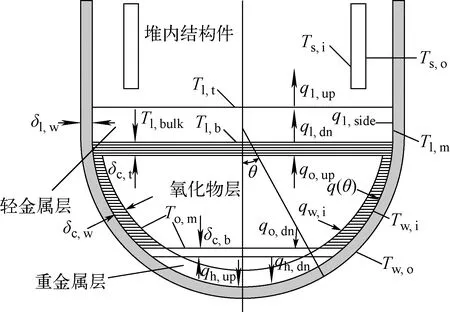
图2 熔池传热模型示意图Fig.2 Molten pool heat transfer model

模型关系式如下(其氧化物层和轻金属层的关系式适用于两层熔池结构)。

中间氧化层：

Qo,vVo=qo,upAo,up+qo,dn(Ao,side+Ao,dn)

(11)

(12)

(13)

(14)

顶部轻金属层：

Ql,vVl+ql,dnAl,dn=ql,upAl,up+ql,sideAl,side

(15)

(16)

(17)

(18)

底部重金属层：

Qh,vVh+qh,upAh,up=qh,dnAh,dn

(19)

(20)

式中：下标o、h、l分别代表氧化层、重金属层、轻金属层；Qo,v、Qh,v、Ql,v为熔池各层的体积功率密度；qo,up、qh,up、ql,up为熔池各层向上的热流密度；qo,dn、qh,dn、ql,dn为熔池各层向下的热流密度；Tl,bulk、Tl,m分别为轻金属层主体温度和熔化温度；Ts,i、Ts,o分别为堆内结构件内、外表面温度；As、Al,up、Al,dn、Al,side为堆内结构件、轻金属层的向上、向下和向侧面的传热面积；Ah,up、Ah,dn分别为重金属层向上、向下的传热面积；Ao,up、Ao,dn、Ao,side分别为氧化层向上、向下和向侧面的传热面积；Nu为努塞尔数；εi、εs分别为轻金属层和结构件的辐射发射率；σ为斯特藩-玻尔兹曼常数；Vo、Vh、Vl为各层的总体积。

熔融池中总的衰变热为停堆t小时后的衰变热Pdecay-FP(t)。Pdecay-FP(t)为输入值，氧化物层的体积功率密度为：

(21)

式中，fo-mUO2/UO2tot为氧化层中二氧化铀占二氧化铀总质量的比例。

2 验证与应用

向清安等[12]已开展了对CISER软件在CIS有效性评价方面的验证，本文着重对敏感性分析程序SALib进行验证。选择线性模型和非线性模型分别对SALib进行线性模型和非线性模型敏感性分析能力的验证。随后基于Khatib-Rahbar等[15]研究中AP1000的熔池初始参数对下封头熔池模型的关键结果参数开展敏感性分析，文中敏感性分析的样本空间均由Sobol sequence[9]生成。

2.1 SALib敏感性分析能力验证

1) 线性模型

假设线性模型f(x1,x2)=ax1+bx2，xi在[0,1]内均匀分布，该模型的理论解为D=a2/2+b2/2，D1=a2/2，D2=b2/2。a=1、b=1、样本容量N=1 000时线性模型的敏感性分析结果对比列于表2。

表2 a=1、b=1、N=1 000时线性模型的敏感性分析结果对比Table 2 Sensitivity analysis result of linear model at a=1, b=1, and N=1 000

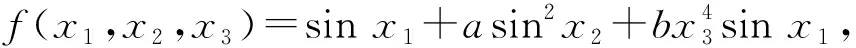
(22)

该模型的敏感性系数计算结果及对比情况列于表3、4。

线性模型与理论解的相对偏差在1%范围内，而非线性模型与理论解的相对偏差在5%范围内，采用Saltelli关系式计算的敏感性系数与Homma[16]结果相当，具有较好的精度。

表3 a=7、b=0.1、N=1 000时非线性模型SiTable 3 Si result of nonlinear model at a=7, b=0.1, and N=1 000

表4 a=7、b=0.1、N=1 000时非线性模型STiTable 4 STi result of nonlinear model at a=7, b=0.1, and N=1 000

2.2 下封头熔池模型的敏感性分析

1) 输入参数

Khatib-Rahbar等[15]利用严重事故系统分析软件MELCOR、MAAP等对压力容器外部成功再淹没条件下的事故进程进行了分析计算，得到了IVR分析的初始参数。IVR分析的初始参数包括初始质量、材料物性、压力容器的几何结构、衰变热等参数，本文选择了锆金属质量、二氧化铀质量等9个代表性输入参数，并假设其在初始参数10%范围内均匀分布(表5[1,15])。

2) 关键结果参数

压力容器下封头外表面的热流密度与测量结果的比值r=qw/qCHF、氧化层硬壳厚度δcr、压力容器壁面厚度δw常被作为CIS有效性评价的指标。本文选择压力容器下封头外表面的热流密度与试验测量结果[1,4,12-13]的比值的平均值(qw/qCHF)avg、最大值(qw/qCHF)max和压力容器壁面厚度的最小值(δw)min及氧化层硬壳厚度的平均值(δcr)avg作为下封头模型评价的关键输出结果。

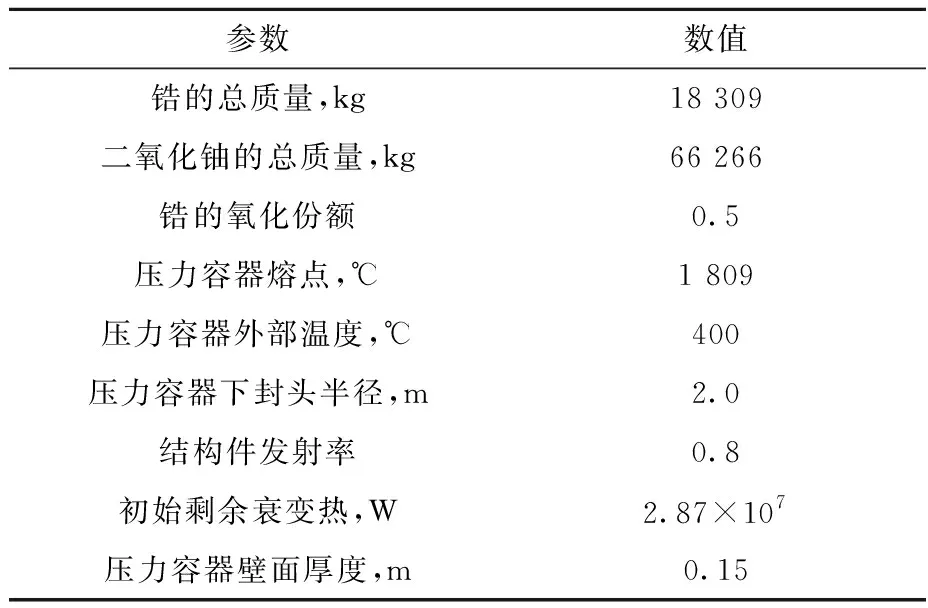
表5 IVR分析初始参数Table 5 Initial parameter of IVR analysis

3) 敏感性系数

Saltelli关系式具有较好的计算效率和精度，本文将采用该关系式计算压力容器下封头壁面热流密度比值等关键结果参数与输入参数之间的敏感性系数，并分析不同样本空间下敏感性系数的收敛性。

(1) 下封头壁面热流密度比值的平均值

图3示出了(qw/qCHF)avg的输入参数敏感性系数，图4示出了(qw/qCHF)avg随下封头半径(图4a)和剩余衰变热(图4b)的变化趋势。

从图3可知，下封头半径和剩余衰变热的敏感性系数分别为0.408和0.544，是影响下封头壁面热流密度比值平均值的关键输入参数。从图4可知，下封头壁面热流密度比值平均值随下封头半径的增加而减小，随剩余衰变热的增加而增加，呈现典型的线性关系。

图3 (qw/qCHF)avg的输入参数敏感性系数Fig.3 Input parameter sensitivity coefficient of (qw/qCHF)avg

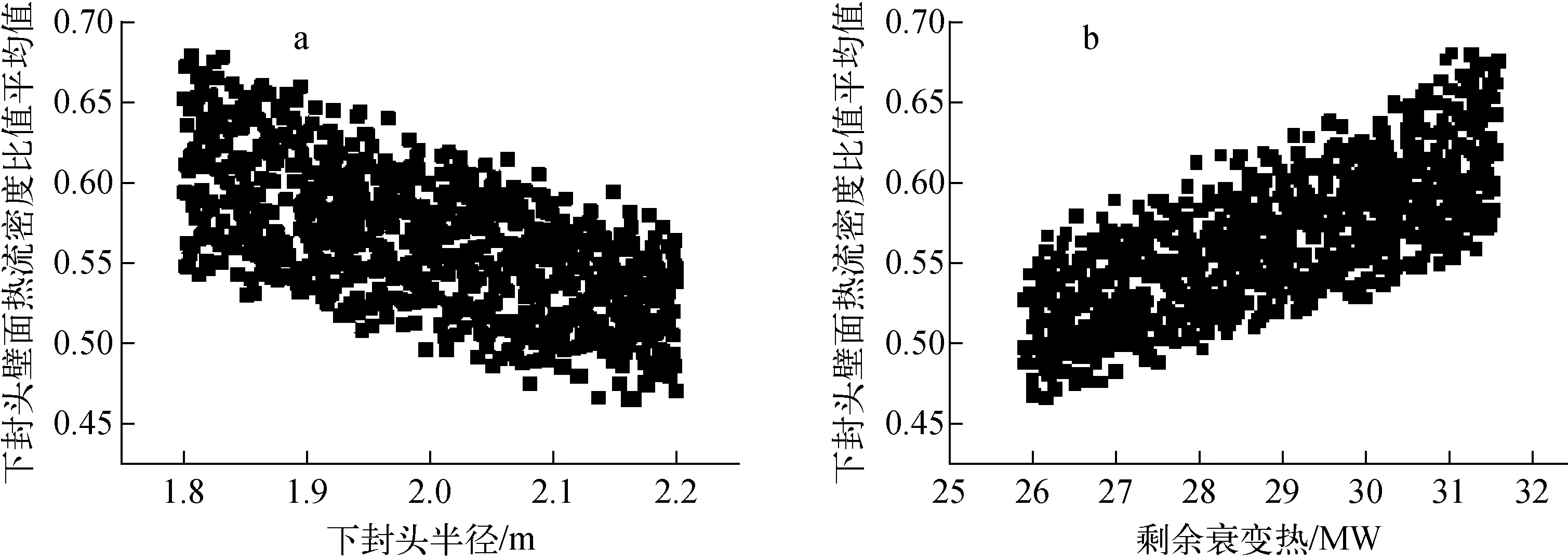
图4 (qw/qCHF)avg随输入参数的变化趋势Fig.4 (qw/qCHF)avg vs. input parameter

(2) 下封头壁面热流密度比值的最大值

图5示出了(qw/qCHF)max的输入参数敏感性系数，图6示出了(qw/qCHF)max随下封头半径(图6a)和剩余衰变热(图6b)的变化趋势。

从图5、6可知，下封头半径和剩余衰变热对(qw/qCHF)max的敏感性系数分别为0.559和0.426，(qw/qCHF)max随下封头半径的增加而减小，随剩余衰变热的增加而增加。由图3和图5可知，剩余衰变热和下封头半径对下封头壁面热流密度比值平均值和最大值的影响程度是不同的。

(3) 氧化层硬壳厚度平均值

图7示出了(δcr)avg的输入参数敏感性系数，图8示出了(δcr)avg随二氧化铀质量等输入参数的变化趋势。

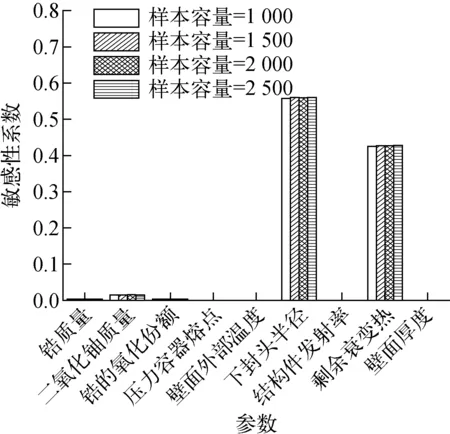
图5 (qw/qCHF)max的输入参数敏感性系数Fig.5 Input parameter sensitivity coefficient of (qw/qCHF)max

图6 (qw/qCHF)max随输入参数的变化趋势Fig.6 (qw/qCHF)max vs. input parameter

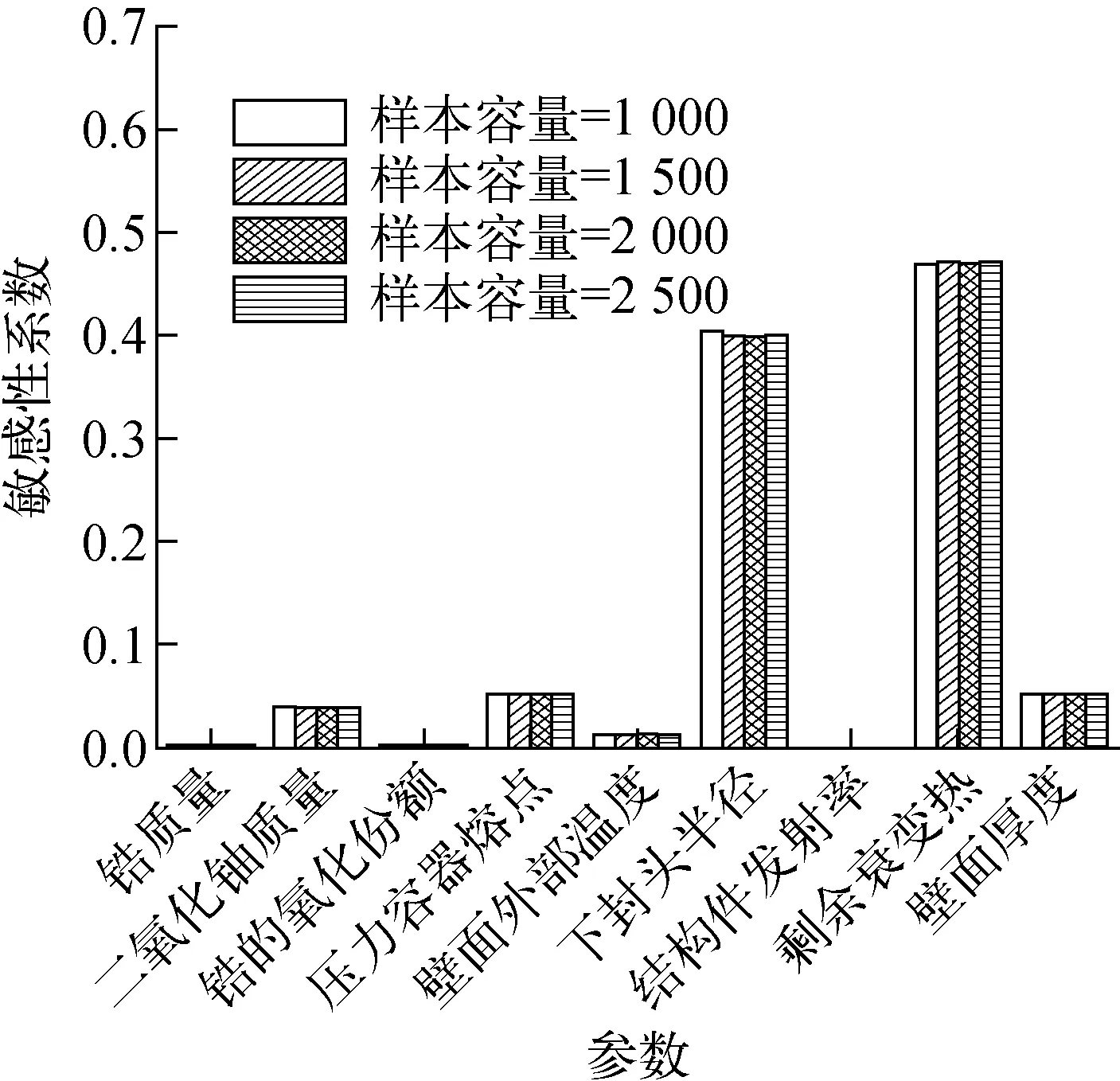
图7 (δcr)avg的输入参数敏感性系数Fig.7 Input parameter sensitivity coefficient of (δcr)avg

从图7可知，二氧化铀质量、压力容器壁面熔点、壁面厚度对(δcr)avg有较小的影响(敏感性系数约0.04～0.05)，下封头半径和剩余衰变热对(δcr)avg的敏感性系数分别为0.4和0.468。由图8可知，(δcr)avg随下封头半径的增加而增加，随剩余衰变热的增加而减小。

(4) 下封头壁面厚度最小值

图9示出了(δw)min的输入参数敏感性系数，图10示出了(δw)min随壁面熔点等输入参数的变化趋势。

从图9可知，壁面熔点和厚度、下封头半径、剩余衰变热对(δw)min有明显的影响，敏感性系数分别为0.275、0.336、0.179和0.162。从图10可知，(δw)min随壁面熔点的增加而增加、随下封头半径的增加而增加、随剩余衰变热的增加而减小。

图8 (δcr)avg随输入参数的变化趋势Fig.8 (δcr)avg vs. input parameter

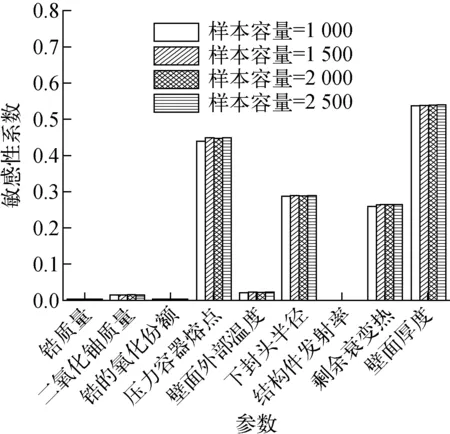
图9 (δw)min的输入参数敏感性系数Fig.9 Input parameter sensitivity coefficient of (δw)min

3 结论

本文采用基于方差分解的全局敏感性分析方法，采用自研的敏感性分析工具SALib和压力容器下封头IVR评价软件CISER对下封头熔池模型开展了关键结果参数与典型输入参数之间的敏感性分析，配合下封头熔池模型关键结果与输入参数的变化趋势图，得到如下结论：

1) 参数样本容量≥1 000时敏感性系数基本趋于一致；

2) 锆质量、二氧化铀质量、锆氧化份额、结构件的发射率的变化对下封头壁面热流密度比值的平均值等关键结果影响较小；

3) 剩余衰变热和下封头半径对熔池下封头模型中的结果参数影响很大，下封头半径的增加，有助于氧化层硬壳厚度的增加，降低壁面热流密度比值;

4) 压力容器壁面熔点的变化对下封头壁面平均厚度有较大的影响，而对壁面热流密度比值和氧化层硬壳厚度平均值的影响较小。

图10 (δw)min随输入参数的变化趋势Fig.10 (δw)min vs. input parameter