基于Kriging-子模型法的混凝土大坝廊道安全分析

戚 蓝，张哲铭

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

在水利工程中，出于对大坝进行灌浆、排水和监测等工作的需要，通常要设置一些孔口或廊道结构。而这些实体上的孔口结构的存在，会对大坝整体的连续性造成一定的影响，从而影响大坝整体的应力分布。研究大坝廊道的应力分布、变形等情况有利于大坝正常工作的运行以及维护工作的及时展开。部分研究者针对混凝土大坝的安全性能进行分析研究并取得了一定的进展，占良红等[1]提出了一种对已存在的部分数据点建立Kriging模型从而预测大坝整体非概率可靠度的方法。程井等[2]采用平稳随机场局部平均法离散理论，推导了基于Neumann展开随机有限元的重力坝结构随机响应计算公式，提出了重力坝可靠度计算方法等。目前关于大坝廊道的安全性能分析等问题中，主要处于使用有限元分析软件建立模型再分析的层面[3-5]，缺少对廊道进行可靠性评估的有效方法，关于大坝廊道可靠度计算的研究还鲜有报道。

本文采用子模型法对大坝廊道进行精细的数值模拟，从而真实清楚地反应廊道周边的应力变形分布情况，在此基础上，结合高预测性能的Kriging算法对大坝廊道进行了非概率可靠度计算分析，从而对大坝廊道的部分安全可靠性能进行分析研究，研究成果可为工程设计提供参考。

1 可靠度计算原理

1.1 混凝土大坝廊道的可靠度计算指标

在考虑大坝廊道的非概率可靠性指标时，由于混凝土大坝廊道的真实应力影响因素较多[6]，若采用x={x1，x2，…，xn}表示结构的尺寸、气温的大小以及荷载效应等不确定性的区间变量，则可以定义功能函数[7]

M=g(x)=f(x1，x2，…，xn)

(1)

式中，g(x)为超曲面，g(x)=0为结构的失效面，g(x)>0结构安全，g(x)<0结构失效。

若用Mc和Mr来表示区间变量M的均值和离差，则可靠度计算指标η可以表示为[8-9]

(2)

若仍采用r和s分别表示结构的抗力作用和荷载效应，可靠度计算指标η经一系列变换后可以表示为[7]

(3)

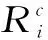
1.2 大坝廊道极限状态计算模型

本文主要考虑混凝土单元的强度破坏，根据俞茂宏的材料强度理论可知，根据材料的3个主应力可以得到的双剪强度理论为[10]

(4)

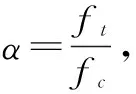
2 基于Kriging算法的可靠度指标计算

在本文求解廊道的可靠度指标时，主要是使用kriging模型来模拟计算式(4)中g(x)的近似函数，建立廊道整体的可靠度计算模型，从而计算廊道各个单元的可靠度指标。

2.1 Kriging模型计算原理

本文所使用的算法来自于MATLAB中的DACE工具箱。其Kriging模型主要是依据已有的离散点的数据建立其响应值的预测，即对于输入量x∈Rn和响应值y(x)∈Rq有

(5)

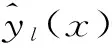
(6)

根据Kriging模型的无偏性和估计方差最小的定义，需要选取最优的θ，使得相关模型R(θ，w，x)尽可能的小。

2.2 Kriging模型选择标准

为了使预测模型的拟合效果与原数据相比较好，采用复相关系数R2反映拟合程度

(7)

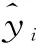
3 工程实例

某供水水库位于敖江流域的中上游，其主要建筑物碾压混凝土重力坝为2级建筑物，从左岸到右岸共分为13个坝段，其中左岸1～6号坝段以及右岸的9～13号坝段为非溢流坝段，7、8号坝段为溢流坝段。该碾压混凝土坝的底部高程103.0 m，顶部高程194.0 m，最大坝高91 m，正常蓄水位190.0 m，设计洪水位190.5 m，校核洪水位192.84 m，廊道分上下两层布置，上层廊道底部高程163.0 m，形式简单，不需要考虑其破坏可能；下层廊道底部高程最低为112.0 m，最高为146.5 m，形式复杂且高程较低，有发生破坏的可能，故本文选取了典型溢流坝段7号坝段下层廊道作为分析研究的对象。

3.1 有限元模型

7号坝段整体模型如图1所示，其坝段下层廊道的有限元模型见图2，共有7 501个单元，2 438个节点。坐标系采用笛卡儿坐标，坐标原点位于上游坝踵处，其中，X轴方向表示顺水流方向，计算范围上下游各取约1.5倍坝高；Y轴方向表示竖直向上方向，计算范围从坝基面(坝基高程为103 m)向下取1.5倍坝高；Z轴方向为坝轴线方向，此计算模型中坝段长27 m。

图1 溢流坝段有限元模型

图2 溢流坝段廊道有限元模型

3.2 材料基本参数与基本荷载

在本文所研究的内容中，材料的基本参数与基本荷载的选择主要是依据工程的实际情况做选择，定值参数包括：混凝土密度为2 330 kg/m3，混凝土泊松比为0.167，地基密度为2 600 kg/m3，上游水位高程192.84 m，上游淤沙高程130.70 m，下游水位高程131.30 m。把实际工程中对结构安全程度影响较大，并且有选择范围的参数作为不定值输入参数，如表1所示。

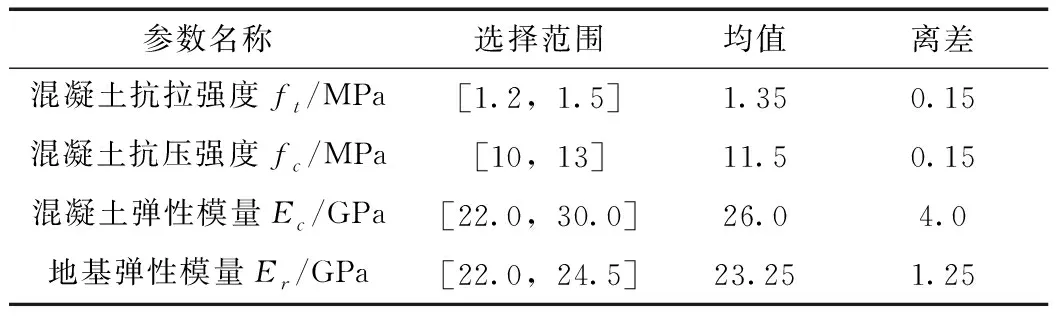
表1 不定值参数

本文为了研究廊道部分最不利的情况，选择了水位最大的校核洪水位的工况，在该工况下，溢流坝段所承受的荷载组合为：自重+上下游水压力+扬压力+淤沙压力。在研究廊道的安全情况时，分别考虑了廊道和大坝为一体(传统廊道)的情况以及预制廊道的情况，当考虑预制廊道时，混凝土面之间的摩擦力为0.55。

3.3 可靠度计算与分析

3.3.1计算步骤

廊道可靠度计算步骤如下：第一步将ANSYS软件计算的廊道部分的应力结果随机选择1 000个单元，提取其3个主应力，作为总样本集；第二步从总样本集中再随机抽选100个单元的3个主应力作为子样本集；第三步使用子样本集的数据点建立Kriging模型，经过一定的迭代次数后寻找到最优的拟合模型；第四步使用Kriging预测对总样本集的数据进行预测，并检查预测模型的复相关系数R2是否满足要求，若不满足要求则重新开始步骤二；第五步使用预测模型得到的数据进行可靠度计算，分析廊道整体的可靠度。

3.3.2传统廊道的可靠度计算

传统廊道按可靠度计算方法进行计算时，经过13次迭代可以计算出最优的参数θ，由于破坏强度的计算与3个主应力均有关，无法直接通过三维图显示，故选取了破坏强度与第一主应力作为坐标显示计算结果，经计算其复相关R2为0.978，说明使用Kriging模型的预测效果良好。原始数据计算所得g(x)见图3a，Kriging模型预测的数据结果见图3b。

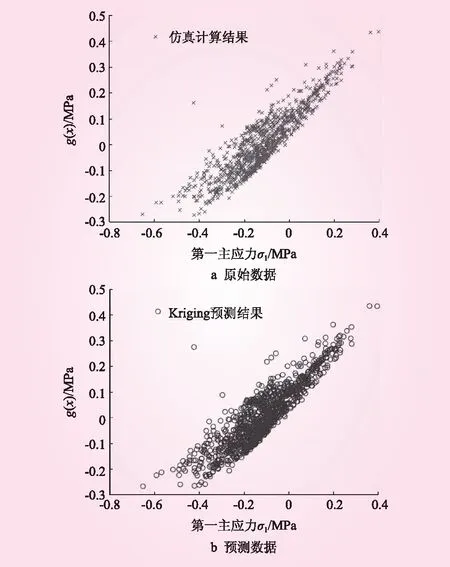
图3 传统廊道Kriging模型计算结果

总样本集的可靠度计算结果见图4。总样本集的情况大致上反应了廊道整体的可靠度分布情况，从图4可以看出，廊道所有部分的可靠度都大于1，处于安全状态。廊道部分可靠度计算的最小值约为2.52，出现在下层廊道上游侧与纵向廊道的交接处，最大值约为8.43，出现在廊道下游侧的底板位置。整体廊道安全可靠，结构设计合理，安全储备充足。

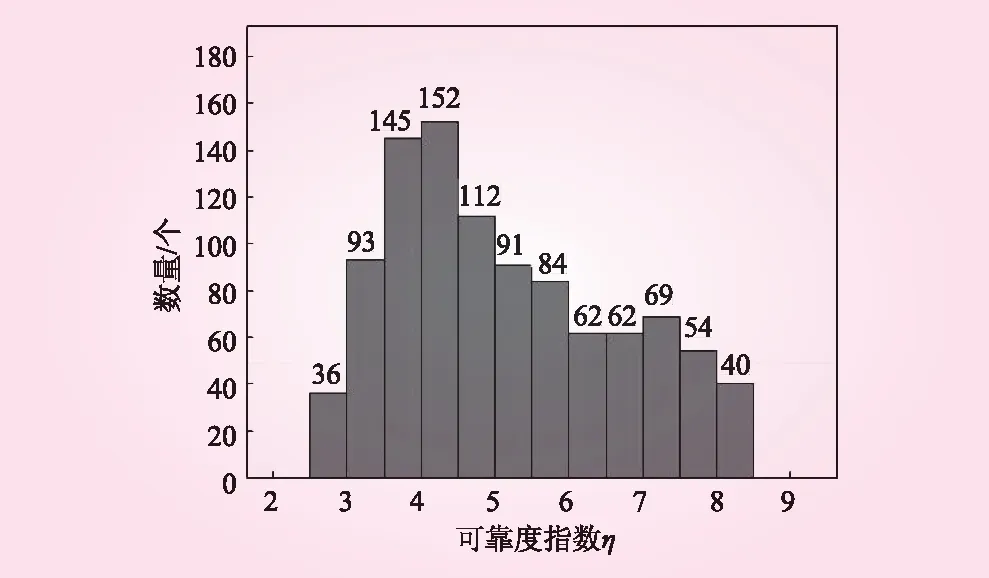
图4 传统廊道总样本集的可靠度统计

3.3.3预制廊道的可靠度计算

本文在考虑预制廊道的可靠度时，仅考虑了混凝土材料的单元强度。在经过17次迭代后可以计算得到最优的θ，其复相关系数R2为0.963，符合要求。原始数据计算所得g(x)见图5a，Kriging模型预测的数据结果见图5b。

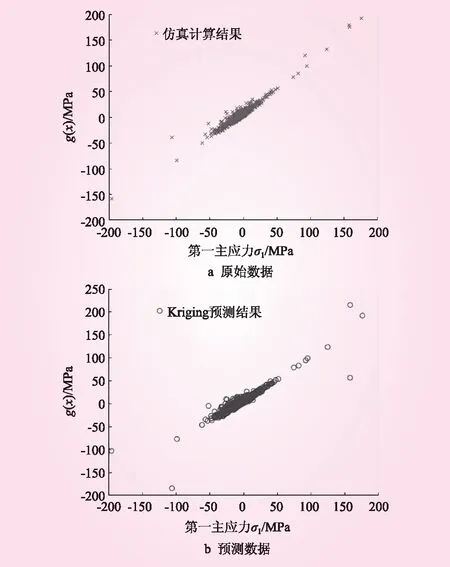
图5 预制廊道Kriging模型计算结果

总样本集的可靠度计算结果见图6。由图6可知，廊道绝大部分的可靠度指标都处于-1<η<0的区间范围内，此时仅考虑廊道的混凝土材料强度已不能满足安全需求。此时其最小值约为-0.99，出现在廊道下游侧骤升段顶部位置，廊道整体在仅考虑混凝土材料强度时是极不安全的，需要进行配筋处理。

图6 预制廊道总样本集的可靠度统计

4 结 论

(1)本文通过Kriging模型与有限元仿真计算软件相结合提出一种廊道可靠度计算指标预测模型，解决了直接评估廊道安全性能不易的问题。

(2)本文提出的模型能够有效地由有限的已知数据点的属性去估计未知的整体数据点的属性，并大大节省了考虑廊道整体结构安全性能时计算时间，使得结构安全计算工作变得简单有效。

(3)本文所述方法仅考虑了材料的单元破坏的一种情况，但其可以推广到多影响因素的可靠度计算中，在实际工程中的廊道应力状态十分复杂，影响因素(如温度、地震等荷载效应)非常多的情况时，该方法也能够有效计算结构的可靠度。